【傅里叶级数与傅里叶变换】数学推导——2、[Part2:T = 2 π的周期函数的傅里叶级数展开] 及 [Part3:周期为2L的函数展开]
文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。
文章全部链接:
基础知识点
Part1:三角函数系的正交性
Part2:T=2π的周期函数的傅里叶级数展开
Part3:周期为T=2L的函数展开
Part4:傅里叶级数的复数形式
Part5:从傅里叶级数推导傅里叶变换
总结
Part2: T = 2 π T = 2 \pi T=2π的周期函数的傅里叶级数展开
假设周期 T = 2 π T = 2 \pi T=2π,将一个周期函数展开为傅里叶级数如下:
f ( x ) = ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) \begin{align} f(x) &= \sum_{n=1}^{\infty} (a_n cos nx + b_n sin nx) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos nx + b_n sin nx \right) & \end{align} f(x)=n=1∑∞(ancosnx+bnsinnx)=2a0+n=1∑∞(ancosnx+bnsinnx)
计算函数中的相关系数 a 0 a_0 a0、 a n a_n an、 b n b_n bn。
第一步,求解 a 0 a_0 a0,对 f ( x ) f(x) f(x)在 [ − π , π ] [-\pi, \pi] [−π,π]之间计算积分 ∫ − π π f ( x ) d x \int_{- \pi}^{\pi} f(x)dx ∫−ππf(x)dx,即为:
∫ − π π f ( x ) d x = a 0 2 ∫ − π π 1 d x + ∫ − π π ∑ n = 1 ∞ a n c o s n x d x + ∫ − π π ∑ n = 1 ∞ b n s i n n x d x \begin{align} & \int_{- \pi}^{\pi} f(x)dx = \frac{a_0}{2} \int_{- \pi}^{\pi} 1 dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx dx +\int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx dx & \end{align} ∫−ππf(x)dx=2a0∫−ππ1dx+∫−ππn=1∑∞ancosnxdx+∫−ππn=1∑∞bnsinnxdx
计算上式第2项
∫ − π π ∑ 1 ∞ a n c o s n x d x = ∫ − π π a 1 c o s x d x + ∫ − π π a 2 c o s 2 x d x + . . . + ∫ − π π a n c o s n x d x + . . . = a 1 ∫ − π π c o s x d x + a 2 ∫ − π π c o s 2 x d x + . . . + a n ∫ − π π c o s n x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_1^{\infty} a_n cos nx dx &= \int_{- \pi}^{\pi} a_1 cos x dx + \int_{- \pi}^{\pi} a_2 cos 2x dx + ... + \int_{- \pi}^{\pi} a_n cos nx dx + ... \\ &= a_1 \int_{- \pi}^{\pi} cos x dx + a_2 \int_{- \pi}^{\pi} cos 2x dx + ... + a_n \int_{- \pi}^{\pi} cos nx dx + ... & \end{align} ∫−ππ1∑∞ancosnxdx=∫−ππa1cosxdx+∫−ππa2cos2xdx+...+∫−ππancosnxdx+...=a1∫−ππcosxdx+a2∫−ππcos2xdx+...+an∫−ππcosnxdx+...
根据三角函数的正交性, ∫ − π π ∑ n = 1 ∞ a n c o s n x d x = 0 \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx dx = 0 ∫−ππ∑n=1∞ancosnxdx=0
计算第3项
∫ − π π ∑ 1 ∞ b n s i n n x d x = ∫ − π π b 1 s i n x d x + ∫ − π π b 2 s i n 2 x d x + . . . + ∫ − π π b n s i n n x d x + . . . = b 1 ∫ − π π s i n x d x + b 2 ∫ − π π s i n 2 x d x + . . . + b n ∫ − π π s i n n x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_1^{\infty} b_n sin nx dx &= \int_{- \pi}^{\pi} b_1 sin x dx + \int_{- \pi}^{\pi} b_2 sin 2x dx + ... + \int_{- \pi}^{\pi} b_n sin nx dx + ... \\ &= b_1 \int_{- \pi}^{\pi} sin x dx + b_2 \int_{- \pi}^{\pi} sin 2x dx + ... + b_n \int_{- \pi}^{\pi} sin nx dx + ... &\end{align} ∫−ππ1∑∞bnsinnxdx=∫−ππb1sinxdx+∫−ππb2sin2xdx+...+∫−ππbnsinnxdx+...=b1∫−ππsinxdx+b2∫−ππsin2xdx+...+bn∫−ππsinnxdx+...
根据三角函数正交性, ∫ − π π ∑ n = 1 ∞ b n s i n n x d x = 0 \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx dx = 0 ∫−ππ∑n=1∞bnsinnxdx=0
那么 ∫ − π π f ( x ) d x = a 0 2 ∫ − π π 1 d x = a 0 2 x ∣ − π π = a 0 2 2 π = π a 0 \int_{- \pi}^{\pi} f(x)dx = \frac{a_0}{2} \int_{- \pi}^{\pi} 1 dx = \frac{a_0}{2} x|_{- \pi}^{\pi} = \frac{a_0}{2} 2 \pi = \pi a_0 ∫−ππf(x)dx=2a0∫−ππ1dx=2a0x∣−ππ=2a02π=πa0,计算求得:
a 0 = 1 π ∫ − π π f ( x ) d x \begin{align} & a_0 = \frac{1}{\pi}\int_{- \pi}^{\pi} f(x)dx & \end{align} a0=π1∫−ππf(x)dx
第二步,计算 a n a_n an,等号两边同时乘以 c o s m x cos mx cosmx,然后在 [ − π , π ] [-\pi, \pi] [−π,π]区间内求积分。如下:
∫ − π π f ( x ) c o s m x d x = a 0 2 ∫ − π π c o s m x d x + ∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x + ∫ − π π ∑ n = 1 ∞ b n s i n n x c o s m x d x \begin{align} & \int_{- \pi}^{\pi} f(x) cos mx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} cosmx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx cos mx dx & \end{align} ∫−ππf(x)cosmxdx=2a0∫−ππcosmxdx+∫−ππn=1∑∞ancosnxcosmxdx+∫−ππn=1∑∞bnsinnxcosmxdx
计算第一项结果为0
a 0 2 ∫ − π π c o s m x d x = a 0 2 ∫ − π π c o s 0 x c o s m x d x = 0 \begin{align} &\frac{a_0}{2} \int_{- \pi}^{\pi} cosmx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} cos 0x cosmx dx = 0 & \end{align} 2a0∫−ππcosmxdx=2a0∫−ππcos0xcosmxdx=0
计算第二项
∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x = ∫ − π π a 1 c o s x c o s m x d x + ∫ − π π a 2 c o s 2 x c o s m x d x + . . . + ∫ − π π a n c o s n x c o s m x d x + . . . = a 1 ∫ − π π c o s x c o s m x d x + a 2 ∫ − π π c o s 2 x c o s m x d x + . . . + a n ∫ − π π c o s n x c o s m x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx &= \int_{- \pi}^{\pi} a_1 cos x cos mx dx + \int_{- \pi}^{\pi} a_2 cos 2x cos mx dx + ... + \int_{- \pi}^{\pi} a_n cos nx cos mx dx + ... \\ & = a_1 \int_{- \pi}^{\pi} cos x cos mx dx + a_2 \int_{- \pi}^{\pi} cos 2x cos mx dx + ... + a_n \int_{- \pi}^{\pi} cos nx cos mx dx + ... & \end{align} ∫−ππn=1∑∞ancosnxcosmxdx=∫−ππa1cosxcosmxdx+∫−ππa2cos2xcosmxdx+...+∫−ππancosnxcosmxdx+...=a1∫−ππcosxcosmxdx+a2∫−ππcos2xcosmxdx+...+an∫−ππcosnxcosmxdx+...
当 m ≠ n m \ne n m=n时
a n ∫ − π π c o s n x c o s m x d x = 0 \begin{align} & a_n \int_{- \pi}^{\pi} cos nx cos mx dx = 0 & \end{align} an∫−ππcosnxcosmxdx=0
当 m = n m=n m=n时,根据三角函数平方公式可得 ∫ − π π c o s n x c o s n x d x = 1 2 [ ∫ − π π 1 d x + ∫ − π π c o s 2 n x d x ] = π \int_{- \pi}^{\pi} cos nx cos nx dx = \frac{1}{2} \left [\int_{- \pi}^{\pi}1dx + \int_{- \pi}^{\pi}cos 2nxdx \right] = \pi ∫−ππcosnxcosnxdx=21[∫−ππ1dx+∫−ππcos2nxdx]=π,该项只会保留当 m = n m=n m=n时的结果,即:
∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x = ∫ − π π a n c o s n x c o s n x d x = π a n \begin{align} & \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx = \int_{- \pi}^{\pi} a_n cos nx cos nx dx = \pi a_n & \end{align} ∫−ππn=1∑∞ancosnxcosmxdx=∫−ππancosnxcosnxdx=πan
计算第三项
∫ − π π ∑ n = 1 ∞ b n s i n n x c o s m x d x = ∫ − π π a 1 s i n x c o s m x d x + ∫ − π π a 2 s i n 2 x c o s m x d x + . . . + ∫ − π π a n s i n n x c o s m x d x + . . . = a 1 ∫ − π π s i n x c o s m x d x + a 2 ∫ − π π s i n 2 x c o s m x d x + . . . + a n ∫ − π π s i n n x c o s m x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx cos mx dx &= \int_{- \pi}^{\pi} a_1 sin x cos mx dx + \int_{- \pi}^{\pi} a_2 sin 2x cos mx dx + ... + \int_{- \pi}^{\pi} a_n sin nx cos mx dx + ... \\ & = a_1 \int_{- \pi}^{\pi} sin x cos mx dx + a_2 \int_{- \pi}^{\pi} sin 2x cos mx dx + ... + a_n \int_{- \pi}^{\pi} sin nx cos mx dx + ... & \end{align} ∫−ππn=1∑∞bnsinnxcosmxdx=∫−ππa1sinxcosmxdx+∫−ππa2sin2xcosmxdx+...+∫−ππansinnxcosmxdx+...=a1∫−ππsinxcosmxdx+a2∫−ππsin2xcosmxdx+...+an∫−ππsinnxcosmxdx+...
由正交性可得第三项为0:
∫ − π π ∑ n = 1 ∞ b n s i n n x c o s m x d x = 0 \begin{align} &\int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx cos mx dx = 0 & \end{align} ∫−ππn=1∑∞bnsinnxcosmxdx=0
那么就有:
∫ − π π f ( x ) c o s n x d x = ∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x = π a n ⇒ a n = 1 π ∫ − π π f ( x ) c o s n x d x \begin{align} & \int_{- \pi}^{\pi} f(x) cos nx dx = \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx = \pi a_n \\ & \Rightarrow \\ & a_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) cos nx dx &\end{align} ∫−ππf(x)cosnxdx=∫−ππn=1∑∞ancosnxcosmxdx=πan⇒an=π1∫−ππf(x)cosnxdx
第三步,计算 b n b_n bn,等式两边乘以 s i n m x sin mx sinmx,然后在区间 [ − π , π ] [-\pi, \pi] [−π,π]之间计算积分,如下:
∫ − π π f ( x ) s i n m x d x = a 0 2 ∫ − π π s i n m x d x + ∫ − π π ∑ n = 1 ∞ a n c o s n x s i n m x d x + ∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x \begin{align} & \int_{- \pi}^{\pi} f(x) sin mx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} sin mx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx sin mx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx & \end{align} ∫−ππf(x)sinmxdx=2a0∫−ππsinmxdx+∫−ππn=1∑∞ancosnxsinmxdx+∫−ππn=1∑∞bnsinnxsinmxdx
计算第一项为0:
a 0 2 ∫ − π π s i n m x d x = a 0 2 ∫ − π π c o s 0 x s i n m x d x = 0 \begin{align} &\frac{a_0}{2} \int_{- \pi}^{\pi} sin mx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} cos 0x sin mx dx = 0 & \end{align} 2a0∫−ππsinmxdx=2a0∫−ππcos0xsinmxdx=0
计算第二项为0:
∫ − π π ∑ n = 1 ∞ a n c o s n x s i n m x d x = ∫ − π π a 1 c o s x s i n m x d x + ∫ − π π a 2 c o s 2 x s i n m x d x + . . . + ∫ − π π a n c o s n x s i n m x d x + . . . = a 1 ∫ − π π c o s x s i n m x d x + a 2 ∫ − π π c o s 2 x s i n m x d x + . . . + a n ∫ − π π c o s n x s i n m x d x + . . . = 0 \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx sin mx dx &= \int_{- \pi}^{\pi} a_1 cos x sin mx dx + \int_{- \pi}^{\pi} a_2 cos 2x sin mx dx + ... + \int_{- \pi}^{\pi} a_n cos nx sin mx dx + ... \\ & = a_1 \int_{- \pi}^{\pi} cos x sin mx dx + a_2 \int_{- \pi}^{\pi} cos 2x sin mx dx + ... + a_n \int_{- \pi}^{\pi} cos nx sin mx dx + ... \\ & = 0 & \end{align} ∫−ππn=1∑∞ancosnxsinmxdx=∫−ππa1cosxsinmxdx+∫−ππa2cos2xsinmxdx+...+∫−ππancosnxsinmxdx+...=a1∫−ππcosxsinmxdx+a2∫−ππcos2xsinmxdx+...+an∫−ππcosnxsinmxdx+...=0
计算第三项
∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x = ∫ − π π b 1 s i n x s i n m x d x + ∫ − π π b 2 s i n 2 x s i n m x d x + . . . + ∫ − π π b n s i n n x s i n m x d x + . . . = b 1 ∫ − π π s i n x s i n m x d x + b 2 ∫ − π π s i n 2 x s i n m x d x + . . . + b n ∫ − π π s i n n x s i n m x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx &= \int_{- \pi}^{\pi} b_1 sin x sin mx dx + \int_{- \pi}^{\pi} b_2 sin 2x sin mx dx + ... + \int_{- \pi}^{\pi} b_n sin nx sin mx dx + ... \\ & = b_1 \int_{- \pi}^{\pi} sin x sin mx dx + b_2 \int_{- \pi}^{\pi} sin 2x sin mx dx + ... + b_n \int_{- \pi}^{\pi} sin nx sin mx dx + ... & \end{align} ∫−ππn=1∑∞bnsinnxsinmxdx=∫−ππb1sinxsinmxdx+∫−ππb2sin2xsinmxdx+...+∫−ππbnsinnxsinmxdx+...=b1∫−ππsinxsinmxdx+b2∫−ππsin2xsinmxdx+...+bn∫−ππsinnxsinmxdx+...
当 m ≠ n m \ne n m=n时
b n ∫ − π π s i n n x s i n m x d x = 0 \begin{align} & b_n \int_{- \pi}^{\pi} sin nx sin mx dx = 0 & \end{align} bn∫−ππsinnxsinmxdx=0
当 m = n m=n m=n时,根据三角函数平方公式可得 ∫ − π π s i n n x s i n n x d x = 1 2 [ ∫ − π π 1 d x − ∫ − π π c o s 2 n x d x ] = π \int_{- \pi}^{\pi} sin nx sin nx dx = \frac{1}{2} \left [\int_{- \pi}^{\pi}1dx - \int_{- \pi}^{\pi}cos 2nxdx \right] = \pi ∫−ππsinnxsinnxdx=21[∫−ππ1dx−∫−ππcos2nxdx]=π,该项只会保留当 m = n m=n m=n时的结果,即:
∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x = ∫ − π π b n s i n ( n x ) s i n ( n x ) d x = π b n \begin{align} & \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx = \int_{- \pi}^{\pi} b_n sin (nx) sin (nx) dx = \pi b_n & \end{align} ∫−ππn=1∑∞bnsinnxsinmxdx=∫−ππbnsin(nx)sin(nx)dx=πbn
那么就有:
∫ − π π f ( x ) s i n n x d x = ∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x = π b n ⇒ b n = 1 π ∫ − π π f ( x ) s i n n x d x \begin{align} & \int_{- \pi}^{\pi} f(x) sin nx dx = \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx = \pi b_n \\ & \Rightarrow \\ & b_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) sin nx dx &\end{align} ∫−ππf(x)sinnxdx=∫−ππn=1∑∞bnsinnxsinmxdx=πbn⇒bn=π1∫−ππf(x)sinnxdx
综上,可以得出,对于一个周期 T = 2 π T=2 \pi T=2π的周期函数,其傅里叶级数为:
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) 其中 , a 0 = 1 π ∫ − π π f ( x ) d x a n = 1 π ∫ − π π f ( x ) c o s n x d x b n = 1 π ∫ − π π f ( x ) s i n n x d x \begin{align} & f(x) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos nx + b_n sin nx \right) \\ & 其中, \\ & a_0 = \frac{1}{\pi}\int_{- \pi}^{\pi} f(x)dx \\ & a_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) cos nx dx \\ & b_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) sin nx dx &\end{align} f(x)=2a0+n=1∑∞(ancosnx+bnsinnx)其中,a0=π1∫−ππf(x)dxan=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx
Part3:周期为 2 L 2L 2L的函数展开
对于一个 T = 2 L T=2L T=2L的周期函数 f ( t ) = f ( t + 2 L ) f(t) = f(t+2L) f(t)=f(t+2L) ,展开傅里叶级数。
换元法令 x = π L t x = \frac{\pi}{L} t x=Lπt,那么 t = L π x t = \frac{L}{\pi} x t=πLx,代入到 f ( t ) f(t) f(t)
f ( t ) = f ( L π x ) \begin{align} & f(t) = f(\frac{L}{\pi}x) & \end{align} f(t)=f(πLx)
令 g ( x ) = f ( t ) = f ( L π x ) g(x) = f(t) = f(\frac{L}{\pi}x) g(x)=f(t)=f(πLx)。
有 x x x与 t t t、 f ( t ) = g ( x ) f(t)=g(x) f(t)=g(x)的换算关系可以得到:
( t = − L ⇔ x = − π ) ⇒ f ( − L ) = g ( − π ) (t=-L \Leftrightarrow x=-\pi) \Rightarrow f(-L) = g(-\pi) (t=−L⇔x=−π)⇒f(−L)=g(−π)
( t = L ⇔ x = π ) ⇒ f ( L ) = g ( π ) (t=L \Leftrightarrow x=\pi) \Rightarrow f(L) = g(\pi) (t=L⇔x=π)⇒f(L)=g(π)
( t = 3 L ⇔ x = 3 π ) ⇒ f ( 3 L ) = g ( 3 π ) (t=3L \Leftrightarrow x= 3\pi) \Rightarrow f(3L) = g(3 \pi) (t=3L⇔x=3π)⇒f(3L)=g(3π)
. . . ... ...
因为 f ( t ) f(t) f(t)是一个周期为 2 L 2L 2L函数,有 f ( − L ) = f ( L ) = f ( 3 L ) . . . f(-L) = f(L) = f(3L)... f(−L)=f(L)=f(3L)...,那么就有 g ( − π ) = g ( π ) = g ( 3 π ) . . . g(-\pi) = g( \pi) = g(3 \pi)... g(−π)=g(π)=g(3π)...,可以看出 g ( x ) g(x) g(x)是一个周期为 2 π 2 \pi 2π的周期函数。
展开 g ( x ) g(x) g(x)傅里叶级数为:
g ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) 其中 , a 0 = 1 π ∫ − π π g ( x ) d x a n = 1 π ∫ − π π g ( x ) c o s n x d x b n = 1 π ∫ − π π g ( x ) s i n n x d x \begin{align} & g(x) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos nx + b_n sin nx \right) \\ & 其中, \\ & a_0 = \frac{1}{\pi}\int_{- \pi}^{\pi} g(x)dx \\ & a_n = \frac{1}{\pi} \int_{- \pi}^{\pi} g(x) cos nx dx \\ & b_n = \frac{1}{\pi} \int_{- \pi}^{\pi} g(x) sin nx dx &\end{align} g(x)=2a0+n=1∑∞(ancosnx+bnsinnx)其中,a0=π1∫−ππg(x)dxan=π1∫−ππg(x)cosnxdxbn=π1∫−ππg(x)sinnxdx
将 x = π L t x = \frac{\pi}{L}t x=Lπt代入,有:
c o s n x = c o s n π L t s i n n x = s i n n π L t g ( x ) = f ( t ) ∫ − π π d x = ∫ − L L d π L t = π L ∫ − L L d t 1 π ∫ − π π d x = 1 π ∫ − L L d π L t = 1 π π L ∫ − L L d t = 1 L ∫ − L L d t \begin{align} cos nx & = cos \frac{n \pi}{L}t \\ sin nx & = sin \frac{n \pi}{L}t \\ g(x) & = f(t) \\ \int_{-\pi}^{\pi} dx & = \int_{-L}^{L} d \frac{\pi}{L}t = \frac{\pi}{L} \int_{-L}^{L}dt \\ \frac{1}{\pi} \int_{-\pi}^{\pi} dx & = \frac{1}{\pi} \int_{-L}^{L} d \frac{\pi}{L}t = \frac{1}{\pi} \frac{\pi}{L} \int_{-L}^{L}dt = \frac{1}{L} \int_{-L}^{L}dt \\ &\end{align} cosnxsinnxg(x)∫−ππdxπ1∫−ππdx=cosLnπt=sinLnπt=f(t)=∫−LLdLπt=Lπ∫−LLdt=π1∫−LLdLπt=π1Lπ∫−LLdt=L1∫−LLdt
代入展开函数有:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n π L t + b n s i n n π L t ) 其中 , a 0 = 1 L ∫ − L L f ( t ) d x a n = 1 L ∫ − L L f ( t ) c o s n π L t d x b n = 1 L ∫ − L L f ( t ) s i n n π L t d x \begin{align} f(t) &= \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos \frac{n \pi}{L}t + b_n sin \frac{n \pi}{L}t \right) \\ & 其中, \\ a_0 &= \frac{1}{L}\int_{- L}^{L} f(t)dx \\ a_n &= \frac{1}{L} \int_{- L}^{L} f(t) cos \frac{n \pi}{L}t dx \\ b_n &= \frac{1}{L} \int_{- L}^{L} f(t) sin \frac{n \pi}{L}t dx &\end{align} f(t)a0anbn=2a0+n=1∑∞(ancosLnπt+bnsinLnπt)其中,=L1∫−LLf(t)dx=L1∫−LLf(t)cosLnπtdx=L1∫−LLf(t)sinLnπtdx
在工程中, t t t从 0 0 0开始,周期 T = 2 L T = 2L T=2L,令 ω = π L = 2 π T \omega = \frac{\pi}{L} = \frac{2 \pi}{T} ω=Lπ=T2π,有 L = π ω L = \frac{\pi}{\omega} L=ωπ
对于周期函数
∫ − L L d t = ∫ 0 2 L d t = ∫ 0 T d t \begin{align} & \int_{-L}^{L} dt = \int_{0}^{2L} dt = \int_{0}^{T} dt &\end{align} ∫−LLdt=∫02Ldt=∫0Tdt
代入上面的展开函数就得到,对于 T = 2 L T=2L T=2L的周期函数,其傅里叶级数展开如下:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n ω t + b n s i n n ω t ) 其中 , a 0 = 1 L ∫ − L L f ( t ) d x a n = 1 L ∫ − L L f ( t ) c o s n ω t d x b n = 1 L ∫ − L L f ( t ) s i n n ω t d x \begin{align} & f(t) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos n \omega t + b_n sin n \omega t \right) \\ & 其中, \\ & a_0 = \frac{1}{L}\int_{- L}^{L} f(t)dx \\ & a_n = \frac{1}{L} \int_{- L}^{L} f(t) cos n \omega t dx \\ & b_n = \frac{1}{L} \int_{- L}^{L} f(t) sin n \omega t dx &\end{align} f(t)=2a0+n=1∑∞(ancosnωt+bnsinnωt)其中,a0=L1∫−LLf(t)dxan=L1∫−LLf(t)cosnωtdxbn=L1∫−LLf(t)sinnωtdx
原视频博主提供了一个示例,计算如下图所示的周期函数的傅里叶展开。
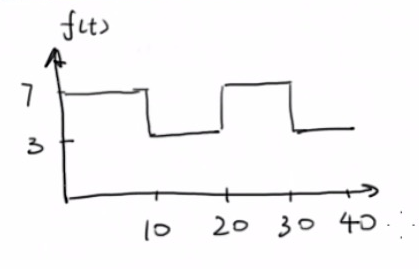
解:
由上图知道周期 T = 2 L = 20 T= 2L = 20 T=2L=20,令 ω = π L = π 10 \omega = \frac{\pi} {L} = \frac{\pi}{10} ω=Lπ=10π。根据上面得到的结论,上图的傅里叶级数展开函数为:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n ω t + b n s i n n ω t ) ,其中 L = 10 a 0 = 1 L ∫ − L L f ( t ) d x a n = 1 L ∫ − L L f ( t ) c o s n ω t d x b n = 1 L ∫ − L L f ( t ) s i n n ω t d x \begin{align} f(t) &= \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos n \omega t + b_n sin n \omega t \right) & ,其中L=10 \\ a_0 &= \frac{1}{L}\int_{- L}^{L} f(t)dx \\ a_n &= \frac{1}{L} \int_{- L}^{L} f(t) cos n \omega t dx \\ b_n &= \frac{1}{L} \int_{- L}^{L} f(t) sin n \omega t dx &\end{align} f(t)a0anbn=2a0+n=1∑∞(ancosnωt+bnsinnωt)=L1∫−LLf(t)dx=L1∫−LLf(t)cosnωtdx=L1∫−LLf(t)sinnωtdx,其中L=10
代入图示函数计算:
a 0 = 1 10 [ ∫ 0 10 7 d x + ∫ 0 10 3 d x ] = 1 10 [ 7 ⋅ ( 10 − 0 ) + 3 ⋅ ( 20 − 10 ) ] = 10 \begin{align} a_0 &= \frac{1}{10} \left[ \int_{0}^{10} 7dx + \int_{0}^{10} 3dx \right] \\ & = \frac{1}{10} \left[ 7 \cdot (10-0) + 3 \cdot (20-10) \right] \\ & = 10 \end{align} a0=101[∫0107dx+∫0103dx]=101[7⋅(10−0)+3⋅(20−10)]=10
a n = 1 10 [ ∫ 0 10 7 c o s n ω t d x + ∫ 10 20 3 c o s n ω t d x ] = 1 10 [ 7 n ω s i n n ω t ∣ 0 10 + 3 n ω s i n n ω t ∣ 10 20 ] = 1 n π [ 7 ( s i n n π − s i n 0 ) + 3 ( s i n 2 n π − s i n n π ) ] = 0 \begin{align} a_n & = \frac{1}{10} \left[ \int_{0}^{10} 7 cos n \omega t dx + \int_{10}^{20} 3 cos n \omega t dx \right] \\ & = \frac{1}{10} \left[ \frac{7}{n \omega} sin n \omega t |_{0}^{10} + \frac{3}{n\omega} sin n \omega t |_{10}^{20} \right] \\ & = \frac{1}{n \pi} \left[ 7 ( sin n \pi - sin 0) + 3 (sin 2n \pi - sin n \pi) \right] \\ & = 0 \end{align} an=101[∫0107cosnωtdx+∫10203cosnωtdx]=101[nω7sinnωt∣010+nω3sinnωt∣1020]=nπ1[7(sinnπ−sin0)+3(sin2nπ−sinnπ)]=0
b n = 1 10 [ ∫ 0 10 7 s i n n ω t d x + ∫ 10 20 3 s i n n ω t d x ] = 1 10 [ − 7 n ω c o s n ω t ∣ 0 10 − 3 n ω c o s n ω t ∣ 10 20 ] = − 1 n π [ 7 ( c o s n π − c o s 0 ) + 3 ( c o s 2 n π − c o s n π ) ] = 4 n π [ 1 − c o s n π ] \begin{align} b_n & = \frac{1}{10} \left[ \int_{0}^{10} 7 sin n \omega t dx + \int_{10}^{20} 3 sin n \omega t dx \right] \\ & = \frac{1}{10} \left[ - \frac{7}{n \omega} cos n \omega t |_{0}^{10}- \frac{3}{n\omega} cos n \omega t |_{10}^{20} \right] \\ & = - \frac{1}{n \pi} \left[ 7 ( cos n \pi - cos 0) + 3 (cos 2n \pi - cos n \pi )\right] \\ & = \frac{4}{n \pi} \left[ 1 - cos n \pi \right] \end{align} bn=101[∫0107sinnωtdx+∫10203sinnωtdx]=101[−nω7cosnωt∣010−nω3cosnωt∣1020]=−nπ1[7(cosnπ−cos0)+3(cos2nπ−cosnπ)]=nπ4[1−cosnπ]
当 n n n是奇数时, c o s n π = − 1 cos n \pi = -1 cosnπ=−1,此时 b n = 8 n π b_n = \frac{8}{n \pi} bn=nπ8;
当 n n n是偶数时, c o s n π = 1 cos n \pi = 1 cosnπ=1,此时 b n = 0 b_n = 0 bn=0;
最后,图示函数的傅里叶级数展开为:
F ( t ) = { 5 + ∑ n = 1 ∞ ( 8 n π s i n n π 10 t ) , n = 2 k + 1 , k ∈ z 5 , n = 2 k , k ∈ z \begin{align} F(t) = \left\{\begin{matrix} 5 + \sum_{n=1}^{\infty} (\frac{8}{n \pi} sin \frac{n \pi}{10} t),& n=2k+1,k \in z \\ 5 , & n=2k,k \in z \end{matrix}\right. \end{align} F(t)={5+∑n=1∞(nπ8sin10nπt),5,n=2k+1,k∈zn=2k,k∈z
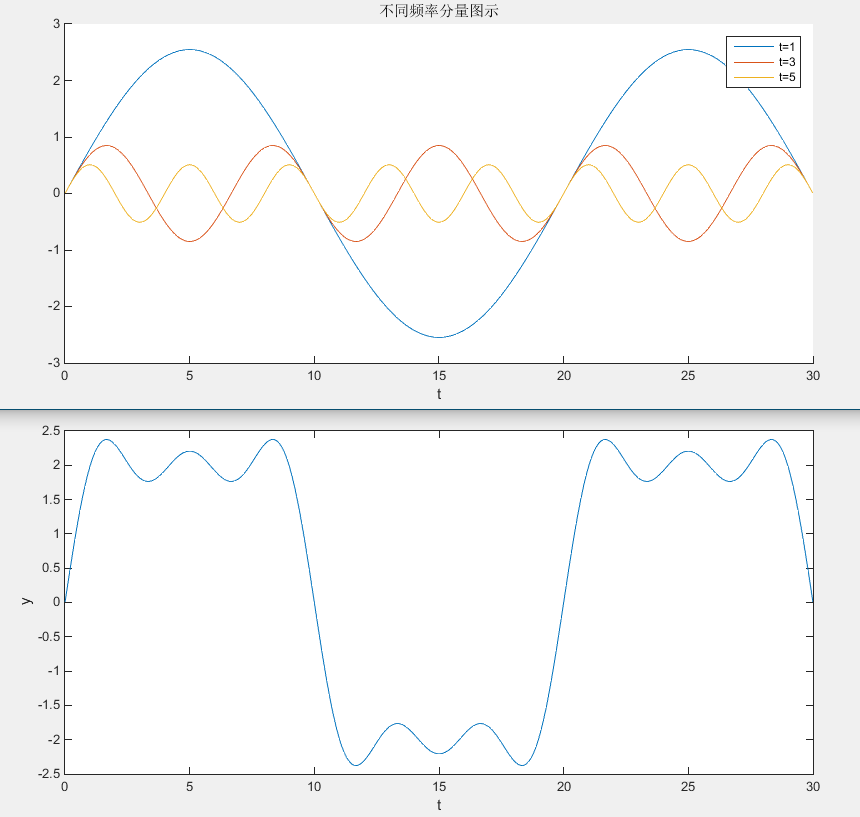
从展开函数中可以发现,当 n n n越大时, 8 n π \frac{8}{n \pi} nπ8越小, n π 10 \frac{n \pi}{10} 10nπ越大即频率越高。现在取 n = 1 , 3 , 5 n=1, 3, 5 n=1,3,5,得到每个频率分量分别为:
n = 1 时为 8 π s i n π 10 t ; n = 3 时为 8 3 π s i n 3 π 10 t ; n = 5 时为 8 5 π s i n 5 π 10 t ; \begin{align} n =1时为 \frac{8}{ \pi} sin \frac{ \pi}{10} t; \\ n = 3 时为 \frac{8}{3 \pi} sin \frac{3 \pi}{10} t; \\ n = 5 时为 \frac{8}{5 \pi} sin \frac{5 \pi}{10} t; \\ \end{align} n=1时为π8sin10πt;n=3时为3π8sin103πt;n=5时为5π8sin105πt;
这三个频率以及它们叠加后的图示如下,可以发现,频率越大,其振幅越小,叠加后的变化大致与给定示意图一致。
相关文章:

【傅里叶级数与傅里叶变换】数学推导——2、[Part2:T = 2 π的周期函数的傅里叶级数展开] 及 [Part3:周期为2L的函数展开]
文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。 文章全部链接: 基础知识点 Part1:三角函数系的正交性 Part2:T2π的周期函数的傅里叶级数展开 P…...
【IMX6ULL驱动开发学习】06.DHT11温湿度传感器驱动程序编写与测试
一、DHT11简介 DHT11是一款可测量温度和湿度的传感器。比如市面上一些空气加湿器,会测量空气中湿度,再根据测量结果决定是否继续加湿。 DHT11数字温湿度传感器是一款含有已校准数字信号输出的温湿度复合传感器,具有超小体积、极低功耗的特点…...

sip开发从理论到实践,让你快速入门sip
目录 引言: sip协议是什么? sip的网络结构(重点) sip的特点 sip使用的url sip协议的应用领域 sip协议基本的消息类型 请求消息 响应消息 sip协议的消息结构(这个是重点) sip的常见会话流程…...

十三、Linux中必须知道的几个快捷键!!!
1、强制停止 当某些代码正在运行时,你想让其停止,只需要按下如下快捷键即可: 【CTRL】【C】 示例: 2、退出 Linux系统自带python3解释器,当你进入python3解释器之后,需要退出时,只需要按下&am…...

Django进阶-文件上传
普通文件上传 定义 用户可以通过浏览器将图片等文件上传到网站 场景 用户上传头像 上传流动性的文档【pdf,txt】等 上传规范-后端 1.视图函数中,用request。FILES取文件框的内容 file request.FILES[xxx] 说明: 1.FILES的key对应页面中…...

clickhouse-数据导入导出方案
一、简介 clickhouse有多种数据的导入导出方式,可以灵活使用,下面对这些方式分别做些介绍,导入导出的写法与格式和格式设置有关。 二、导入 1.从s3导入 详情可查看官网,也可以在这里获取数据集 -- 建库建表 CREATE DATABASE …...

[JavaWeb]【一】入门JavaWeb开发总概及HTML、CSS、JavaScript
目录 一 特色 二 收获编辑 三 什么是web? 四 网站的工作流程 五 web网站的开发模式编辑 六 web开发课程学习安排 七、初始web前端 八 HTML、CSS 8.1 什么是HTNL\CSS(w3cschool) 8.2 HTML快速入门 8.3 VS Code开发工具 8.3.1 插件 8.3.2 主题(改变颜色&…...
Python自动化小技巧18——自动化资产月报(word设置字体表格样式,查找替换文字)
案例背景 每月都要写各种月报,经营管理月报,资产月报.....这些报告文字目标都是高度相似的,只是需要替换为每个月的实际数据就行,如下: (打码是怕信息泄露.....) 可以看到,这个报告的都是高度模板化&…...
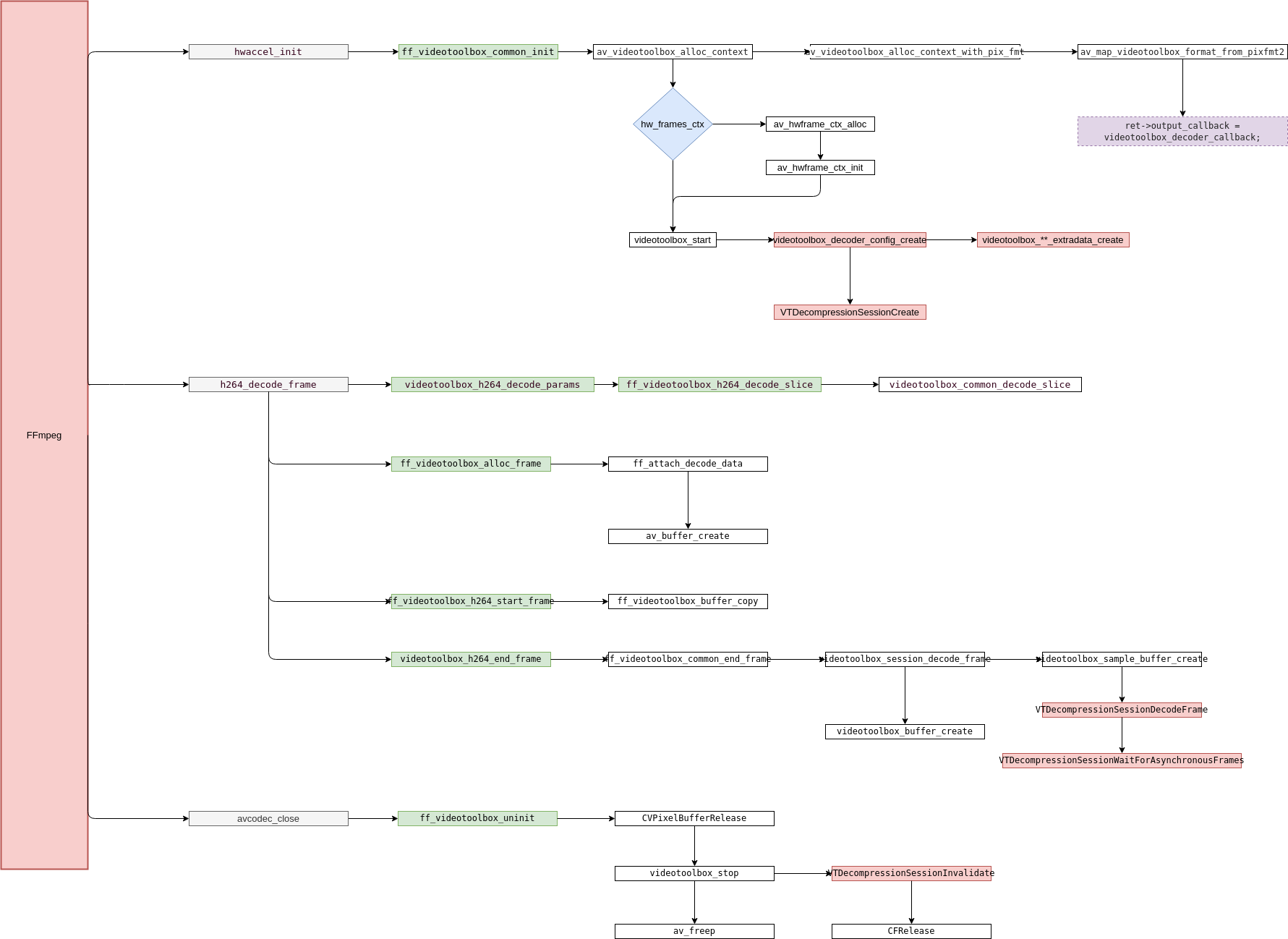
FFmpeg5.0源码阅读——VideoToobox硬件解码
摘要:本文描述了FFmpeg中videotoobox解码器如何进行解码工作,如何将一个编码的码流解码为最终的裸流。 关键字:videotoobox,decoder,ffmpeg VideoToolbox 是一个低级框架,提供对硬件编码器和解码器的直接访问。 它提供视频…...

IDEA 中Tomcat源码环境搭建
一、从仓库中拉取源代码 配置仓库地址、项目目录;点击Clone按钮,从仓库中拉取代码 Tomcat源码对应的github地址: https://github.com/apache/tomcat.git 二、安装Ant插件 打开 File -> Setting -> Plugins 三、添加Build文件 &…...
MATLAB | 七夕节用MATLAB画个玫瑰花束叭
Hey又是一年七夕节要到了,每年一次直男审美MATLAB绘图大赛开始hiahiahia,真的这些代码越写越不知道咋写,又不想每年把之前的代码翻出来再发一遍,于是今年又对我之前写的老代码进行了点优化组合,整了个花球变花束&#…...

嵌入式开发之configure
1 前述 在Linux的应用或者驱动开发过程中,编写makefile是无法避免的问题,但是由于makefile的各种规则,或显式,或隐式,非常多,不经常写的话,很难写出一个可用的makefile文件。为了“偷懒”&…...

深入浅出Pytorch函数——torch.nn.Module
分类目录:《深入浅出Pytorch函数》总目录 Pytorch中所有网络的基类,我们的模型也应该继承这个类。Modules也可以包含其它Modules,允许使用树结构嵌入他们,我们还可以将子模块赋值给模型属性。 语法 torch.nn.Module(*args, **kwargs)方法 …...
【100天精通python】Day38:GUI界面编程_PyQt 从入门到实战(中)_数据库操作与多线程编程
目录 专栏导读 4 数据库操作 4.1 连接数据库 4.2 执行 SQL 查询和更新: 4.3 使用模型和视图显示数据 5 多线程编程 5.1 多线程编程的概念和优势 5.2 在 PyQt 中使用多线程 5.3 处理多线程间的同步和通信问题 5.3.1 信号槽机制 5.3.2 线程安全的数据访问 Q…...
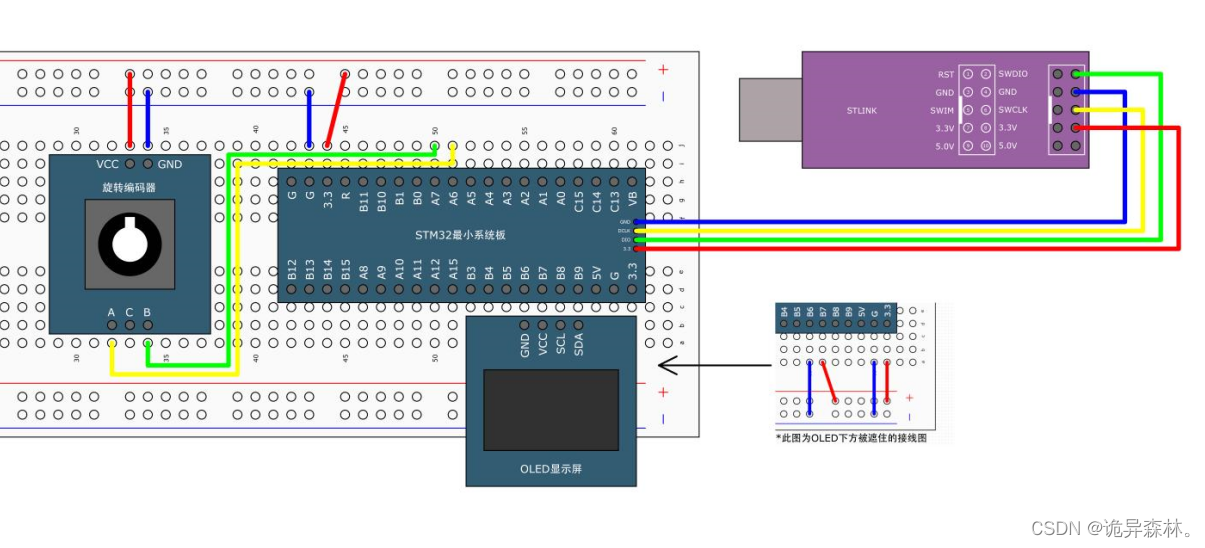
STM32--TIM定时器(3)
文章目录 输入捕获简介频率测量输入捕获通道输入捕获基本结构PWMI的基本结构输入捕获模式测量PWM频率和占空比代码 编码器接口正交编码器工作模式接口基本结构TIM编码接口器测速代码: 输入捕获简介 输入捕获IC(Input Capture),是处理器捕获外部输入信号…...
爬虫框架- feapder + 爬虫管理系统 - feaplat 的学习简记
文章目录 feapder 的使用feaplat 爬虫管理系统部署 feapder 的使用 feapder是一款上手简单,功能强大的Python爬虫框架 feapder 官方文档 文档写的很详细,可以直接上手。 基本命令: 创建爬虫项目 feapder create -p first-project创建爬虫 …...

设计模式详解-享元模式
类型:结构型模式 实现原理:尝试重用现有的同类对象,如果未找到匹配的对象,则创建新对象 目的:减少创建对象的数量以减少内存占用和提高性能。 解决的问题:大量的对象可能造成的内存溢出问题 解决方法&a…...

BDA初级分析——用SQL筛选数据
一、用SQL对数据分组 GROUP BY Group by,按...分组 作用:根据给定字段进行字段的分组,通常和聚合函数配合使用,实现分组的分析 写法:select ...from ...group by 字段名 (也可以是多个字段) GROUP BY的逻辑 SELECT gender,COUNT(user_id) …...
(成功踩坑)electron-builder打包过程中报错
目录 注意:文中的解决方法2,一定全部看完,再进行操作,有坑 背景 报错1: 报错2: 1.原因:网络连接失败 2.解决方法1: 3.解决方法2: 3.1查看缺少什么资源文件 3.2去淘…...
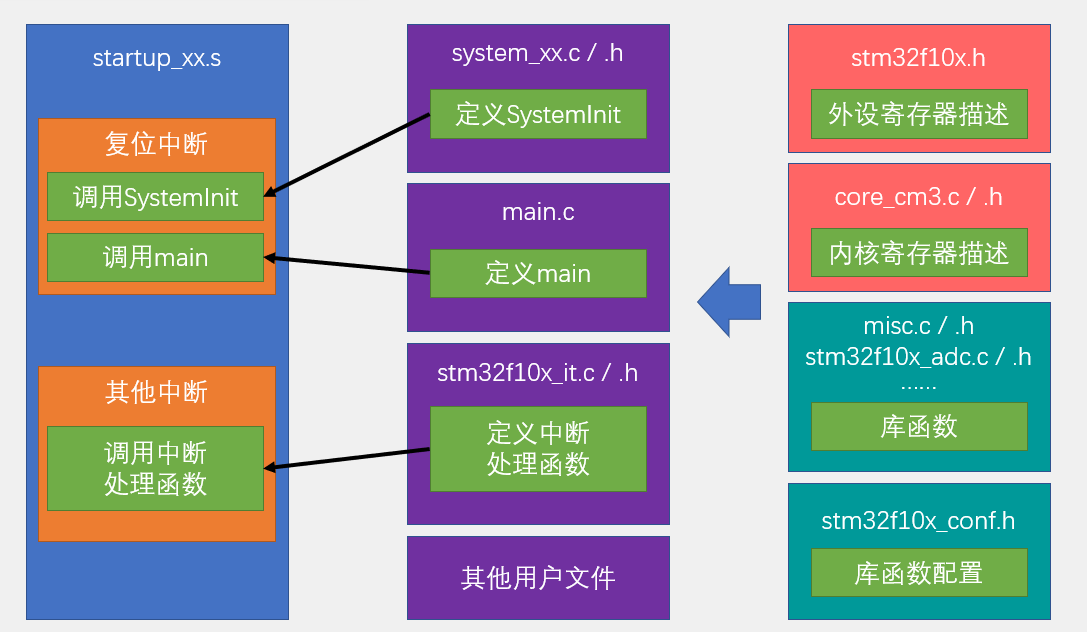
【STM32】 工程
🚩 WRITE IN FRONT 🚩 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四" 🔎🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2022博客之星TO…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
