sklearn学习-朴素贝叶斯
文章目录
- 一、概述
- 1、真正的概率分类器
- 2、sklearn中的朴素贝叶斯
- 二、不同分布下的贝叶斯
- 1、高斯朴素贝叶斯GaussianNB
- 2、探索贝叶斯:高斯朴素贝叶斯擅长的数据集
- 3、探索贝叶斯:高斯朴素贝叶斯的拟合效果与运算速度
- 总结
一、概述
1、真正的概率分类器
算法得出的结论,永远不是100%确定的,更多的是判断出了一种“样本的标签更可能是某类的可能
性”,而非一种“确定”。
朴素贝叶斯是一种直接衡量标签和特征之间的概率关系的有监督学习算法,是一种专注分类的算法。朴素贝叶斯的算法根源就是基于概率论和数理统计的贝叶斯理论,因此它是根正苗红的概率模型。接下来,我们就来认识一下这个简单快速的概率算法。
假设有两个随机变量X和Y,他们分别可以取值为x和y。有这两个随机变量,我们可以定义两种概率:
关键概念:联合概率与条件概率:
联合概率:“X取值为x”和“Y取值为y”两个事件同时发生的概率,表示为

条件概率:在”X取值为x“的前提下,”Y取值为y“的概率,表示为
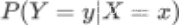
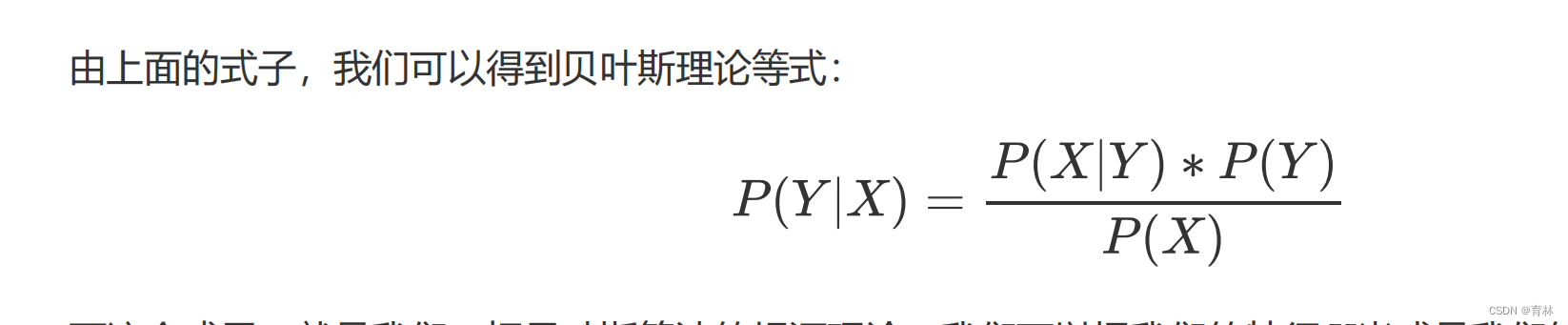
而这个式子,就是我们一切贝叶斯算法的根源理论。我们可以把我们的特征 当成是我们的条件事件,而我们要求解的标签 当成是我们被满足条件后会被影响的结果,而两者之间的概率关系就是 P(X|Y),这个概率在机器学习中,被我们称之为是标签的后验概率(posterior probability),即是说我们先知道了条件,再去求解结果。而标签 在没有任何条件限制下取值为某个值的概率,被我们写作 P(Y),与后验概率相反,这是完全没有任何条件限制的,标签的先验概率(prior probability)。而我们的 P(X|Y)被称为“类的条件概率”,表示当Y的取值固定的时候,X为某个值的概率。
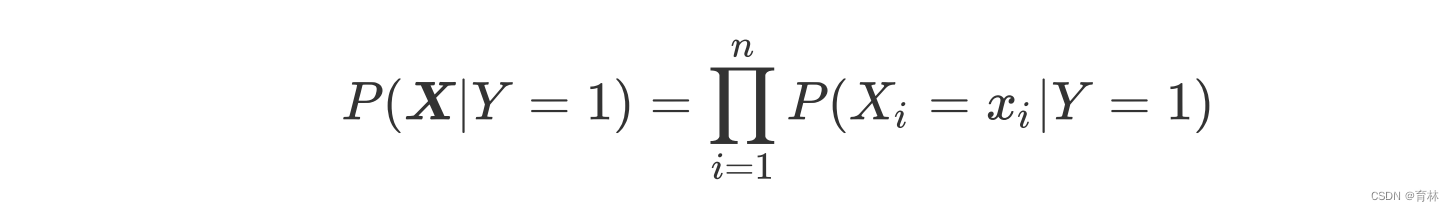
这个式子证明,在Y=1的条件下,多个特征的取值被同时取到的概率,就等于Y=1的条件下,多个特征的取值被分别取到的概率相乘。
假设特征之间是有条件独立的,可以解决众多问题,也简化了很多计算过程,这是朴素贝叶斯被称为”朴素“的理由。
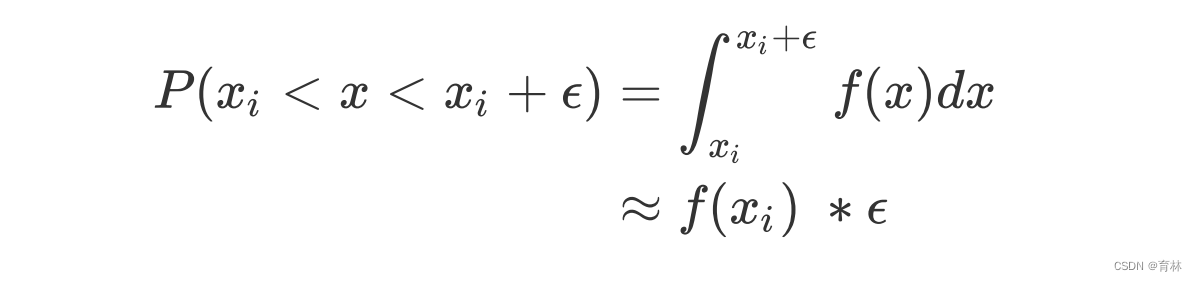
2、sklearn中的朴素贝叶斯
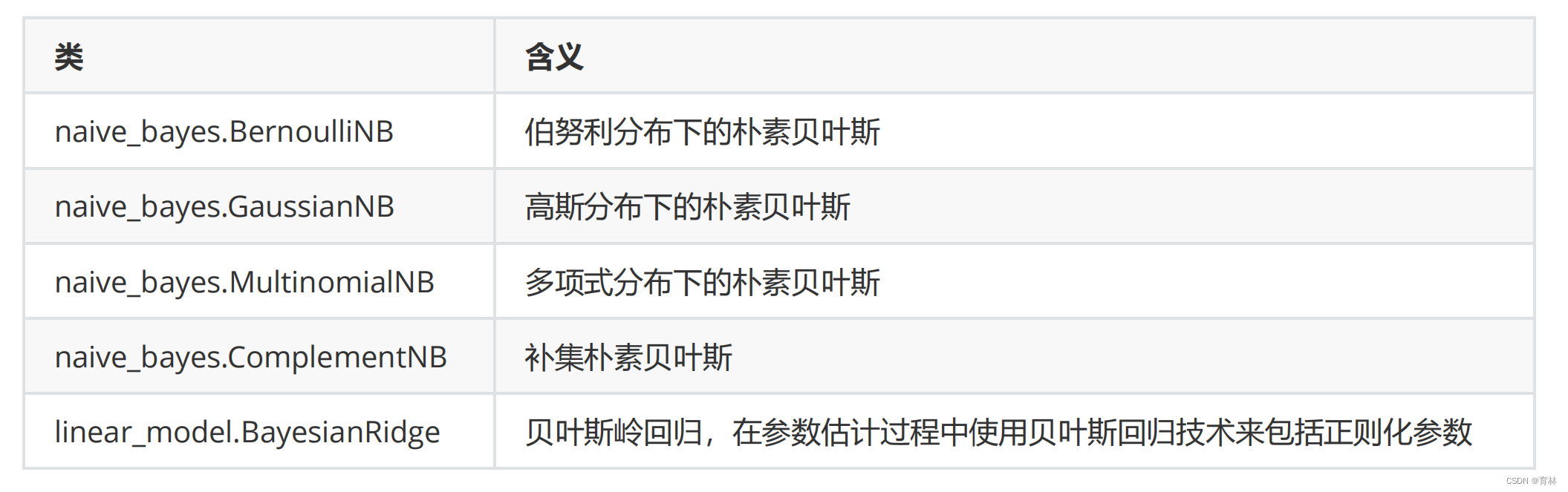
虽然朴素贝叶斯使用了过于简化的假设,这个分类器在许多实际情况中都运行良好,著名的是文档分类和垃圾邮件过滤。而且由于贝叶斯是从概率角度进行估计,它所需要的样本量比较少,极端情况下甚至我们可以使用1%的数据作为训练集,依然可以得到很好的拟合效果。当然,如果样本量少于特征数目,贝叶斯的效果就会被削弱。
二、不同分布下的贝叶斯
1、高斯朴素贝叶斯GaussianNB
class sklearn.naive_bayes.GaussianNB (priors=None, var_smoothing=1e-09)
高斯朴素贝叶斯有如下公式:
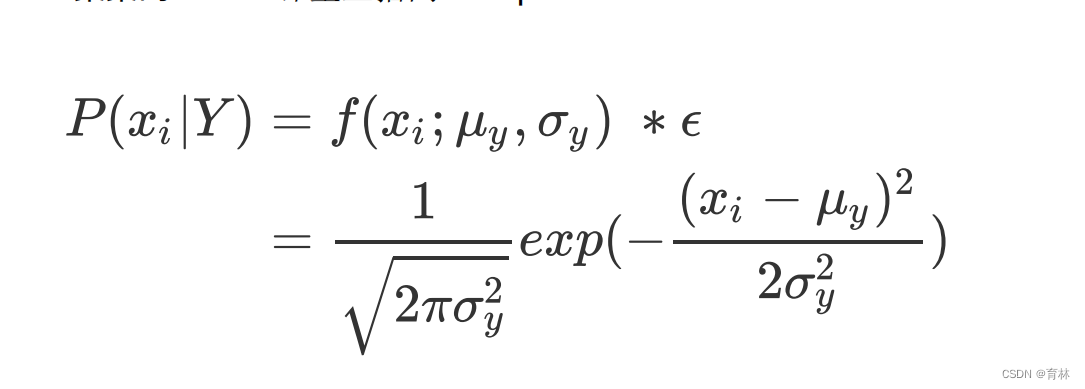

但在实例化的时候,我们不需要对高斯朴素贝叶斯类输入任何的参数,调用的接口也全部sklearn中比较标准的一些搭配,可以说是一个非常轻量级的类,操作非常容易。但过于简单也意味着贝叶斯没有太多的参数可以调整,因此贝叶斯算法的成长空间并不是太大,如果贝叶斯算法的效果不是太理想,我们一般都会考虑换模型。
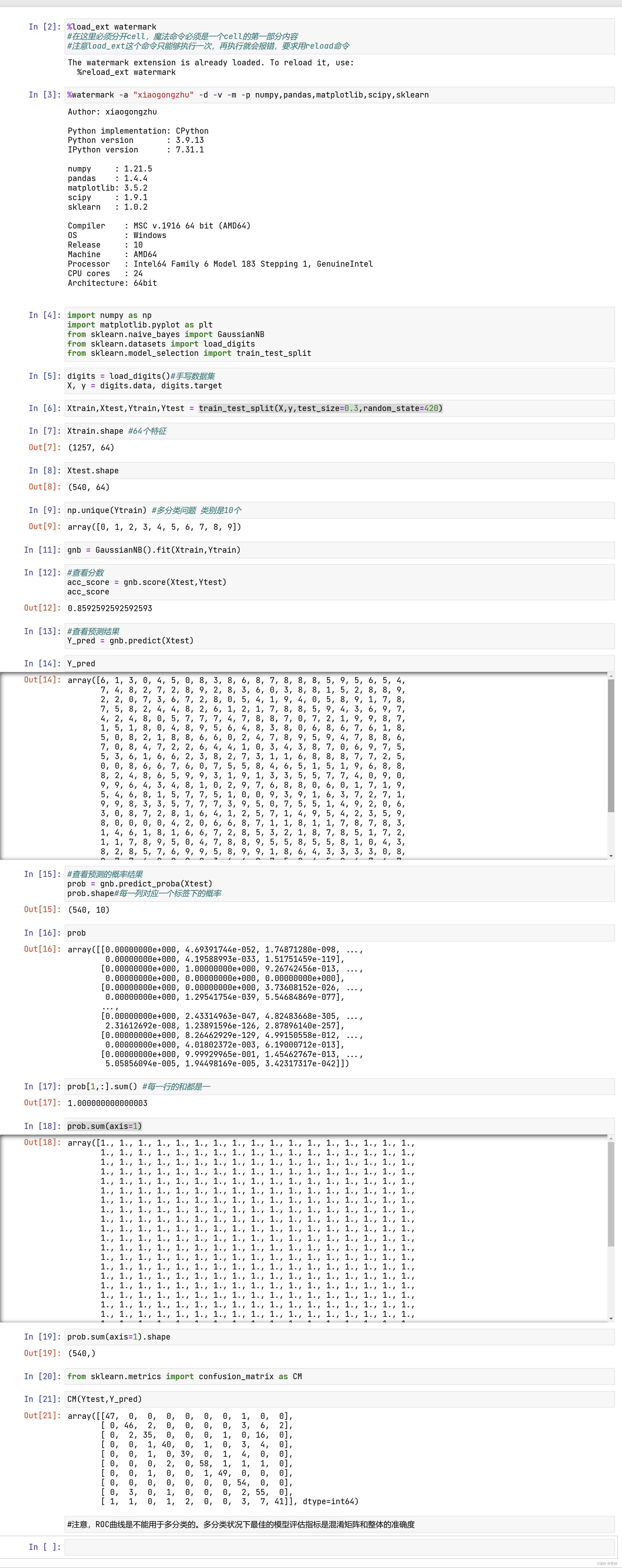
2、探索贝叶斯:高斯朴素贝叶斯擅长的数据集
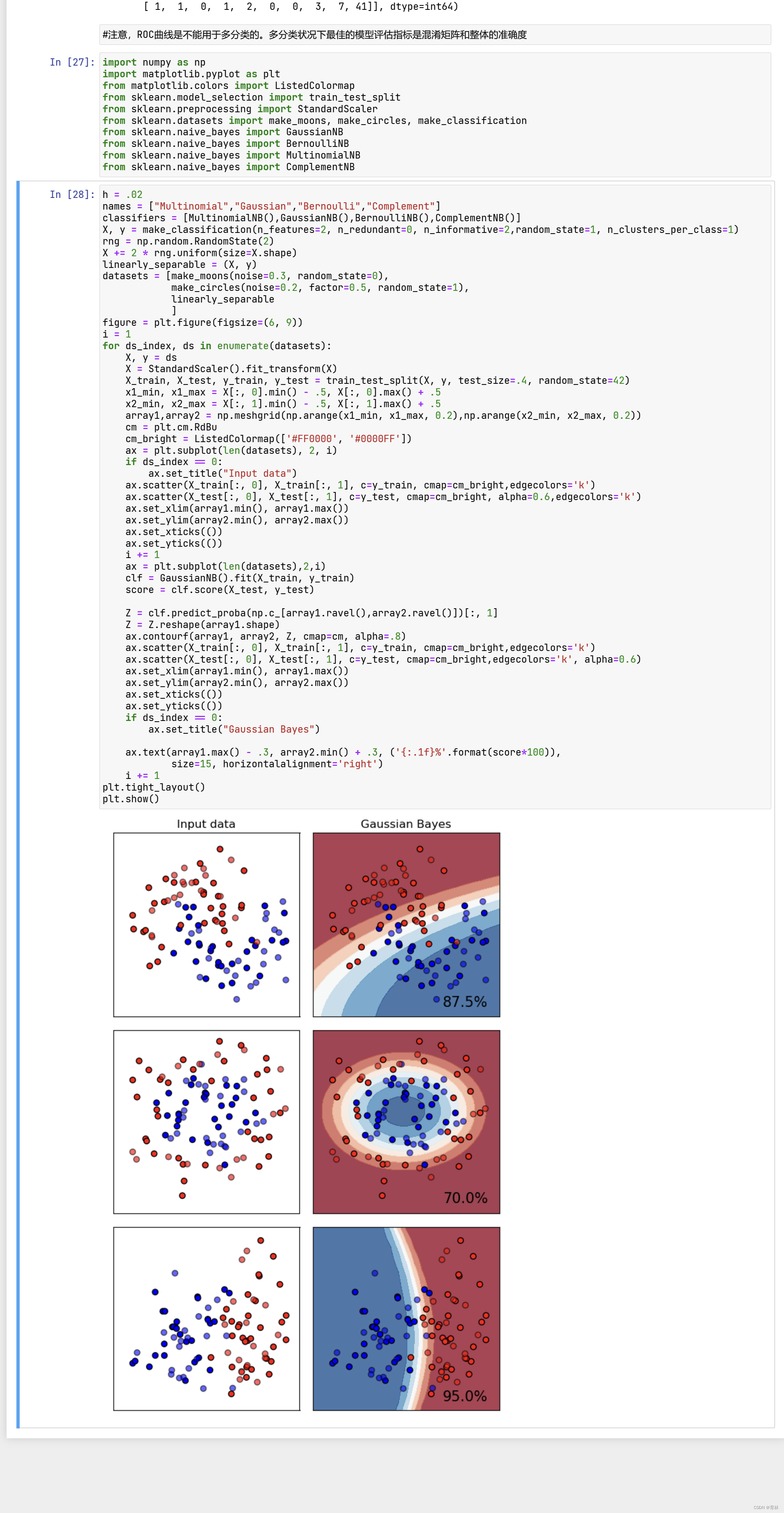
从图上来看,高斯贝叶斯属于比较特殊的一类分类器,其分类效果在二分数据和月亮型数据上表现优秀,但是环形数据不太擅长。我们之前学过的模型中,许多线性模型比如逻辑回归,线性SVM等等,在线性数据集上会绘制直线决策边界,因此难以对月亮型和环形数据进行区分,但高斯朴素贝叶斯的决策边界是曲线,可以是环形也可以是弧线,所以尽管贝叶斯本身更加擅长线性可分的二分数据,但朴素贝叶斯在环形数据和月亮型数据上也可以有远远胜过其他线性模型的表现。
3、探索贝叶斯:高斯朴素贝叶斯的拟合效果与运算速度
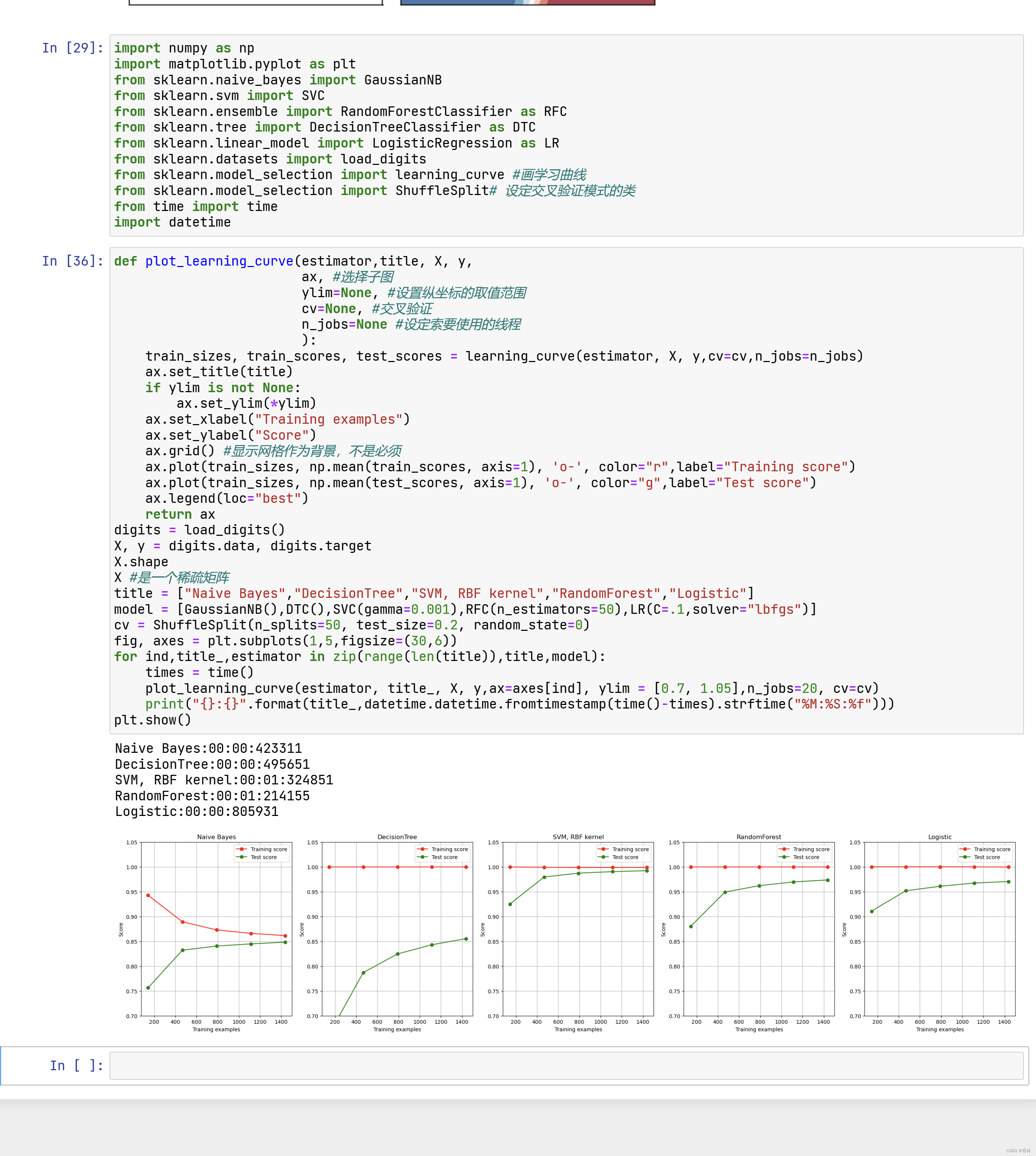
我们首先返回的结果是各个算法的运行时间。可以看到,决策树和贝叶斯不相伯仲(如果你没有发现这个结果,那么可以多运行几次,你会发现贝叶斯和决策树的运行时间逐渐变得差不多)。决策树之所以能够运行非常快速是因为sklearn中的分类树在选择特征时有所“偷懒”,没有计算全部特征的信息熵而是随机选择了一部分特征来进行计算,因此速度快可以理解,但我们知道决策树的运算效率随着样本量逐渐增大会越来越慢,但朴素贝叶斯却可以在很少的样本上获得不错的结果,因此我们可以预料,随着样本量的逐渐增大贝叶斯会逐渐变得比决策树更快。朴素贝叶斯计算速度远远胜过SVM,随机森林这样复杂的模型,逻辑回归的运行受到最大迭代次数的强烈影响和输入数据的影响(逻辑回归一般在线性数据上运行都比较快,但在这里应该是受到了稀疏矩阵的影响)。因此在运算时间上,朴素贝叶斯还是十分有优势的。
紧接着,我们来看一下每个算法在训练集上的拟合。手写数字数据集是一个较为简单的数据集,决策树,森林,SVC和逻辑回归都成功拟合了100%的准确率,但贝叶斯的最高训练准确率都没有超过95%,这也应证了我们最开始说的,朴素贝叶斯的分类效果其实不如其他分类器,贝叶斯天生学习能力比较弱。并且我们注意到,随着训练样本量的逐渐增大,其他模型的训练拟合都保持在100%的水平,但贝叶斯的训练准确率却逐渐下降,这证明样本量越大,贝叶斯需要学习的东西越多,对训练集的拟合程度也越来越差。反而比较少量的样本可以让贝叶斯有较高的训练准确率。
再来看看过拟合问题。首先一眼看到,所有模型在样本量很少的时候都是出于过拟合状态的(训练集上表现好,测试集上表现糟糕),但随着样本的逐渐增多,过拟合问题都逐渐消失了,不过每个模型的处理手段不同。比较强大的分类器们,比如SVM,随机森林和逻辑回归,是依靠快速升高模型在测试集上的表现来减轻过拟合问题。相对的,决策树虽然也是通过提高模型在测试集上的表现来减轻过拟合,但随着训练样本的增加,模型在测试集上的表现善生却非常缓慢。朴素贝叶斯独树一帜,是依赖训练集上的准确率下降,测试集上的准确率上升来逐渐解决过拟合问题。
接下来,看看每个算法在测试集上的拟合结果,即泛化误差的大小。随着训练样本数量的上升,所有模型的测试表现都上升了,但贝叶斯和决策树在测试集上的表现远远不如SVM,随机森林和逻辑回归。SVM在训练数据量增大到1500个样本左右的时候,测试集上的表现已经非常接近100%,而随机森林和逻辑回归的表现也在95%以上,而决策树和朴素贝叶斯还徘徊在85%左右。但这两个模型所面临的情况十分不同:决策树虽然测试结果不高,但是却依然具有潜力,因为它的过拟合现象非常严重,我们可以通过减枝来让决策树的测试结果逼近训练结果。然而贝叶斯的过拟合现象在训练样本达到1500左右的时候已经几乎不存在了,训练集上的分数和测试集上的分数非常接近,只有在非常少的时候测试集上的分数才能够比训练集上的结果更高,所以我们基本可以判断,85%左右就是贝叶斯在这个数据集上的极限了。可以预测到,如果我们进行调参,那决策树最后应该可以达到90%左右的预测准确率,但贝叶斯却几乎没有潜力了。
在这个对比之下,我们可以看出:贝叶斯是速度很快,但分类效果一般,并且初次训练之后的结果就很接近算法极限的算法,几乎没有调参的余地。也就是说,如果我们追求对概率的预测,并且希望越准确越好,那我们应该先选择逻辑回归。如果数据十分复杂,或者是稀疏矩阵,那我们坚定地使用贝叶斯。如果我们分类的目标不是要追求对概率的预测,那我们完全可以先试试看高斯朴素贝叶斯的效果(反正它运算很快速,还不需要太多的样本),如果效果很不错,我们就很幸运地得到了一个表现优秀又快速的模型。如果我们没有得到比较好的结果,那我们完全可以选择再更换成更加复杂的模型。
总结
相关文章:

sklearn学习-朴素贝叶斯
文章目录一、概述1、真正的概率分类器2、sklearn中的朴素贝叶斯二、不同分布下的贝叶斯1、高斯朴素贝叶斯GaussianNB2、探索贝叶斯:高斯朴素贝叶斯擅长的数据集3、探索贝叶斯:高斯朴素贝叶斯的拟合效果与运算速度总结一、概述 1、真正的概率分类器 算法…...

分享112个HTML艺术时尚模板,总有一款适合您
分享112个HTML艺术时尚模板,总有一款适合您 112个HTML艺术时尚模板下载链接:https://pan.baidu.com/s/1D3-mfPOud-f3vy9yLl-bmw?pwdfph2 提取码:fph2 Python采集代码下载链接:采集代码.zip - 蓝奏云 时尚平面模特网站模板 潮…...

用GDB远程调试运行于QEMU的程序
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 测试环境 本文使用 Ubuntu 16.04.4 LTS QEMU 环境进行调试。 3. 用 GDB 调试 QEMU 内程序 3.1 编写用来调试的程序 我们用 ARM32 来进行调试…...
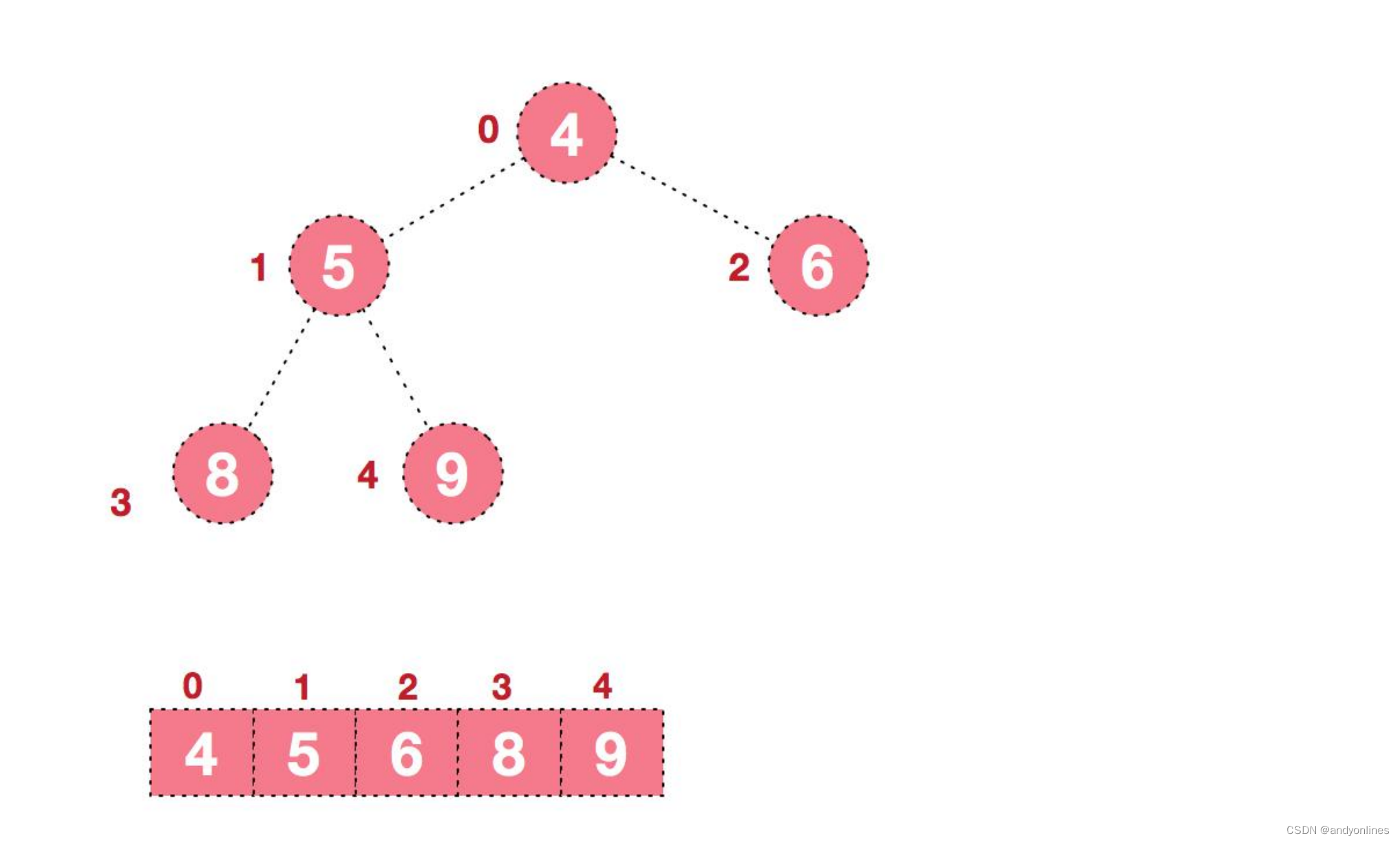
20 堆排序
文章目录1 堆排序的概念2 堆排序基本思想3 堆排序步骤图解说明4 堆排序的代码实现1 堆排序的概念 1) 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为 O(nlogn)…...
2023最新文件快递柜系统网站源码 | 匿名口令分享 | 临时文件分享
内容目录一、详细介绍二、效果展示1.部分代码2.效果图展示三、学习资料下载一、详细介绍 2023最新文件快递柜系统网站源码 | 匿名口令分享 | 临时文件分享 很多时候,我们都想将一些文件或文本传送给别人,或者跨端传递一些信息,但是我们又不…...
)
分片策略(二)
分片策略 基本概念 分片键 用于分片的字段,是将数据库或表拆分的字段,比如,我可以使用user_id作为分片键将用户数据分到不同的表中,这里的user_id就是分片键,除了这种单字段分片,ShardingSphere还支持多…...
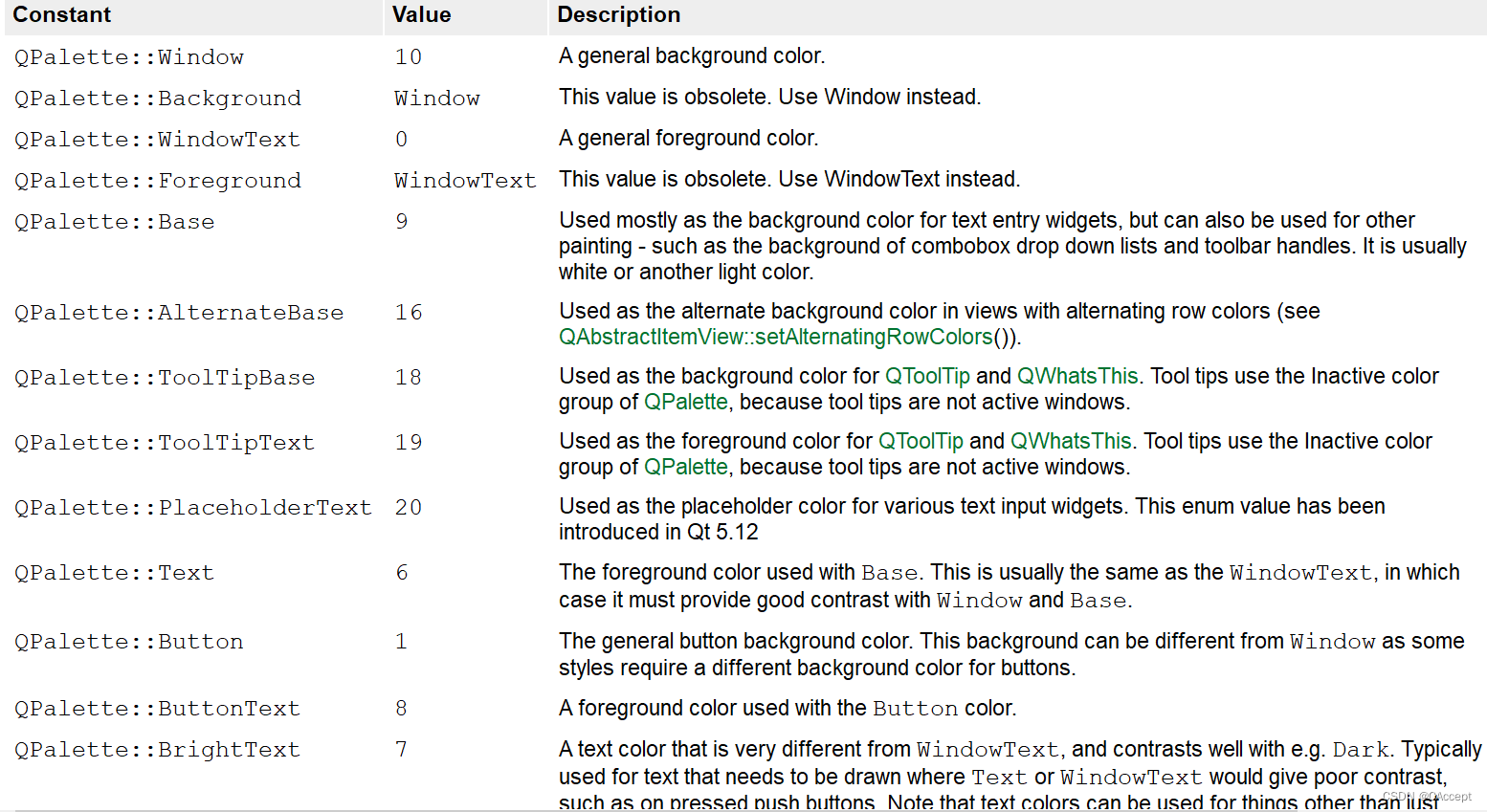
Qt之调色板类QPalette的使用
文章目录QPalette调色板类前言代码知识点讲解QPalette调色板类 前言 Qt提供的调色板类QPalette专门用于管理部件的外观显示,相当于部件或对话框的调色板,管理他们所有的颜色信息。每个部件都包含一个QPalette对象,在显示时,按照…...
Kotlin 32. Kotlin 多语言支持
Kotlin 多语言支持 对于 Kotlin 来说,当我们新建一个项目时,会默认在 values/ 文件夹下,生成一个 strings.xml 文件。比如说, <resources><string name"app_name">exampleNewProject</string> <…...
【Flutter入门到进阶】Dart进阶篇---DartVM单线程设计原理
1 虚拟机的指令执行设计 1.1 虚拟机的分类 基于栈的虚拟机,比如JVM虚拟机 基于寄存器的虚拟机,比如Dalvik虚拟机 1.2 虚拟机的概念 首先问一个基本的问题,作为一个虚拟机,它最基本的要实现哪些功能? 他应该能够模拟…...
的交集)
Dem和NvM(NVRAM Manager)的交集
NVRAM(NvM)提供了在NVRAM中存储数据Block的机制。 NVRAM Block(最大大小取决于配置)被分配给Dem,并由Dem实现事件状态信息和相关数据的永久存储(例如通电复位)。 ECU 状态管理器(Ec…...

AI神经网络CNN/RNN/DNN/SNN的区别对比
@版权声明: 本文由 ChatGpt 创作; BiliBili: https://www.bilibili.com/video/BV17D4y1P7pM/?share_source=copy_web&vd_source=6d217e0ff6387a749dc570aba51d36fd 引言 随着人工智能技术的发展,神经网络作为人工智能的核心技术之一,被广泛应用于图像识别、语音识别、…...

【JavaWeb】一文学会JPA
✅✅作者主页:🔗孙不坚1208的博客 🔥🔥精选专栏:🔗JavaWeb从入门到精通(持续更新中) 📋📋 本文摘要:本篇文章主要介绍JPA的概念、注解实现ORM规范…...
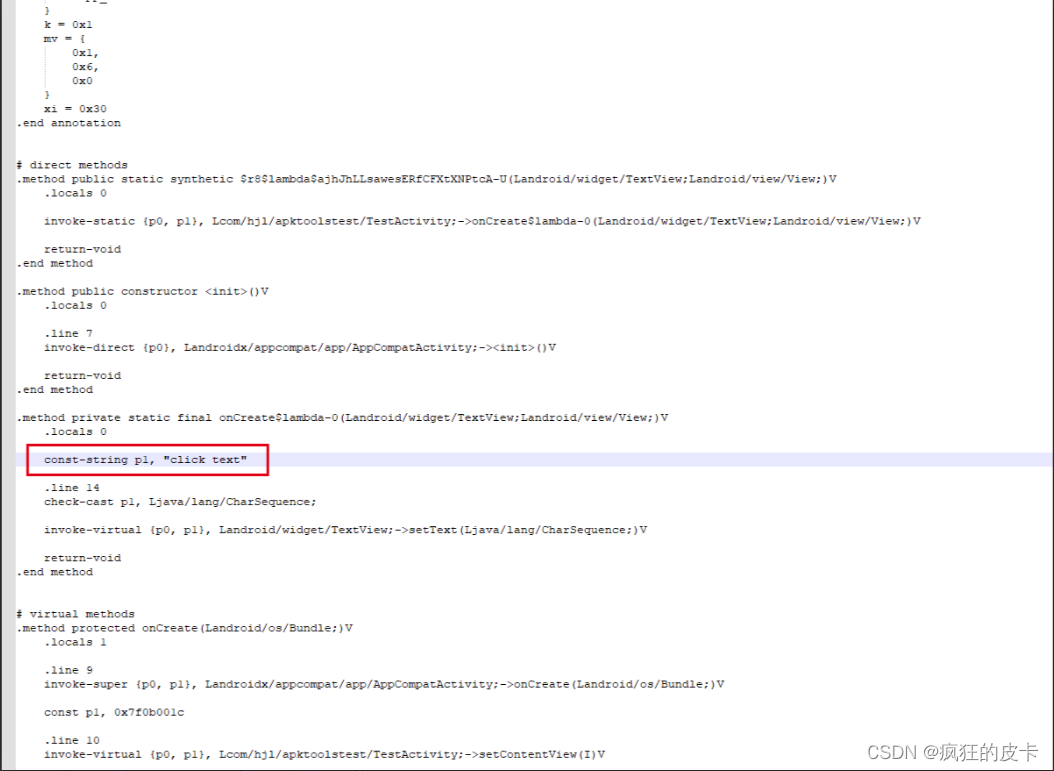
【安卓逆向】APK修改与反编译回编译
【安卓逆向】反编译修改APK回编译使用工具流程步骤Apktool相关安装与使用常用命令备查APK签名命令备查实战练习反编译查看修改的地方使用Apktool反编译得到产物文件夹并进行修改回编APK实用场景在日常开发我们可能需要替换某些资源或者修改某些代码,但是我们没有源码…...

【计组笔记04】计算机组成原理之多模块存储器、Cache高速缓存存储器、Cache地址映射
这篇文章,主要介绍计算机组成原理之多模块存储器、Cache高速缓存存储器、Cache地址映射。 目录 一、双口RAM和多模块存储器 1.1、存取周期 1.2、双口RAM 1.3、多模块存储器...

英语基础-状语的应用
1. 非谓语动词作状语 1. 试着翻译下列句子 当他是一个小孩子的时候,他很喜欢玩电脑游戏。 When he was a child, he liked playing computer games. 如果他通过考试,他妈妈就会给他买一台新电脑。 If he passes the examination, his mother will b…...
)
发表论文需要注意的两点(建议收藏)
在学习人工智能的过程中,论文有着重要的作用,无论是深入学术科研,还是毕业找工作,都离不开发表论文这一步骤,所以今天就和大家分享一些关于论文发表的经验,希望对大家有所帮助。 为什么要早点发表论文&…...

ISTQB-TM-大纲
1. 测试过程 1.1 简介 在 ISTQB 软件测试基础级认证大纲中已描述了基本的测试过程包括以下活动: 计划和控制分析和设计实施和执行评估出口准则和报告测试结束活动 基础级大纲认同这些活动虽然有逻辑顺序,但过程中的某些活动可能重叠,或并行…...
Java SPI 机制详解
在面向对象的设计原则中,一般推荐模块之间基于接口编程,通常情况下调用方模块是不会感知到被调用方模块的内部具体实现。一旦代码里面涉及具体实现类,就违反了开闭原则。如果需要替换一种实现,就需要修改代码。 为了实现在模块装…...
)
腾讯前端经典react面试题(附答案)
React 性能优化在哪个生命周期?它优化的原理是什么? react的父级组件的render函数重新渲染会引起子组件的render方法的重新渲染。但是,有的时候子组件的接受父组件的数据没有变动。子组件render的执行会影响性能,这时就可以使用s…...

Go语言基础(十五):垃圾回收机制(三色标记)
文章目录一、标记清除(三色标记)大致原理1、标记细节2、root对象二、垃圾回收触发机制垃圾回收(Garbage Collection),是一种自动管理内存的机制。传统编程语言(如C/C)需要开发者对无用内存资源进…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
