【视觉SLAM入门】5.2. 2D-3D PNP 3D-3D ICP BA非线性优化方法 数学方法SVD DLT
"养气之学,戒之躁急"
- 1. 3D-2D PNP
- 1.1 代数法
- 1.1.1 DLT(直接线性变换法)
- 1.1.2. P3P
- 1.2 优化法
- BA (Bundle Adjustment)法
- 2. 3D-3D ICP
- 2.1 代数法
- 2.1.1 SVD方法
- 2.2 优化(BA)法
- 2.2.2 非线性优化方法
前置事项:
1. 3D-2D PNP
该问题描述为:当我们知道n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿
1.1 代数法
1.1.1 DLT(直接线性变换法)
解决的问题:已知空间点 P = ( X , Y , Z , 1 ) T P = (X, Y, Z, 1)^T P=(X,Y,Z,1)T 和它投影点 x 1 = ( u 1 , v 1 , 1 ) T x_1 = (u_1, v_1, 1)^T x1=(u1,v1,1)T。求解相机位姿 R , t \boldsymbol {R, t} R,t。
为求解,定义增广矩阵
[ R ∣ t ] = ( t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 ) \boldsymbol {[R| t]} = \begin{pmatrix} t_1&t_2&t_3&t_4 \\\;\\ t_5&t_6&t_7&t_8 \\\;\\ t_9&t_{10}&t_{11}&t_{12} \end{pmatrix} [R∣t]= t1t5t9t2t6t10t3t7t11t4t8t12
我们的目的就是求解这个增广矩阵,利用坐标关系得到:
s ( u 1 v 1 1 ) = ( t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 ) ( X Y Z 1 ) s\begin{pmatrix} u_1&v_1&1 \end{pmatrix} = \begin{pmatrix} t_1&t_2&t_3&t_4 \\\;\\ t_5&t_6&t_7&t_8 \\\;\\ t_9&t_{10}&t_{11}&t_{12} \end{pmatrix}\begin{pmatrix} X&Y&Z&1 \end{pmatrix} s(u1v11)= t1t5t9t2t6t10t3t7t11t4t8t12 (XYZ1)
- 最后一行可以求出 s \boldsymbol s s , 则方程中有12个未知数,需要至少六对点, 可以线性变换 ;
- 匹配点大于6对时,可以用SVD等方法对超定方程做最小二乘;
- 缺点:忽略了旋转矩阵自身约束 ----> 找一个旋转矩阵近似(QR分解),把结果重新投影到 S E ( 3 ) SE(3) SE(3) 流形。
1.1.2. P3P
三对(世界坐标系下)3D-2D(成像平面)匹配点 + 一对验证点。原理图如下:

根据相似三角形的相似关系
Δ O a b − Δ O A B , Δ O b c − Δ O B C , Δ O a c − Δ O A C ⇓ 有如下关系 O A 2 + O B 2 − 2 O A ⋅ O B ⋅ c o s < a , b > = A B 2 O B 2 + O C 2 − 2 O B ⋅ O C ⋅ c o s < b , c > = B C 2 O A 2 + O C 2 − 2 O A ⋅ O C ⋅ c o s < a , c > = A C 2 \Delta Oab - \Delta OAB, \quad \Delta Obc - \Delta OBC, \quad \Delta Oac - \Delta OAC \\\;\\\Downarrow 有如下关系 \\\;\\OA^2 + OB^2 -2OA\cdot OB \cdot cos<a,b> = AB^2\\ OB^2 + OC^2 -2OB\cdot OC \cdot cos<b,c> = BC^2 \\ OA^2 + OC^2 -2OA\cdot OC \cdot cos<a,c> = AC^2 ΔOab−ΔOAB,ΔObc−ΔOBC,ΔOac−ΔOAC⇓有如下关系OA2+OB2−2OA⋅OB⋅cos<a,b>=AB2OB2+OC2−2OB⋅OC⋅cos<b,c>=BC2OA2+OC2−2OA⋅OC⋅cos<a,c>=AC2
记 x = O A / O C , y = O B / O C , v = A B 2 / O C 2 , u v = B C 2 / O C 2 , w v = A C 2 / O C 2 x=OA/OC\quad, y = OB/OC,\quad v=AB^2/OC^2,\quad uv=BC^2/OC^2,\quad wv=AC^2/OC^2 x=OA/OC,y=OB/OC,v=AB2/OC2,uv=BC2/OC2,wv=AC2/OC2
-
推理可得:
( 1 − u ) y 2 − u x 2 − c o s < b , c > y + 2 u x y ⋅ c o s < a , b > + 1 = 0 ( 1 − w ) x 2 − w y 2 − c o s < a , c > x + 2 w x y ⋅ c o s < a , b > + 1 = 0 (1-u)y^2-ux^2-cos<b,c>y+2uxy\cdot cos<a,b>+1=0 \\(1-w)x^2-wy^2-cos<a,c>x+2wxy\cdot cos<a,b>+1=0 (1−u)y2−ux2−cos<b,c>y+2uxy⋅cos<a,b>+1=0(1−w)x2−wy2−cos<a,c>x+2wxy⋅cos<a,b>+1=0 -
求解完成,其中只有 x , y x,y x,y未知,二元二次方程组,可以用吴氏消化法求解。最终最多得到4个解,用验证点对进行验证,得到正确的点即可。
- 只利用3对点的信息,无法利用更多
- 如果点收到噪声影响,算法失效
- 改进的有 E P n P , U P n P EPnP, UPnP EPnP,UPnP
1.2 优化法
BA (Bundle Adjustment)法
- 利用最小化重投影误差来做,简单来说就是已经有相机位姿,然后用该位姿预测得到预测值,再用 预测减观测(投影) 为误差构建最小二乘问题,重新优化相机位姿和空间点位置。重投影示意图如下:

一种通用做法:用来对PnP或ICP的结果进行优化。
- 假设通过PnP已经获得相机的位姿(不精确的) R , t \boldsymbol {R, t} R,t ,它的李代数为 ξ \boldsymbol \xi ξ;
- n个三维空间点 P i = [ X i , Y i , Z i ] T \boldsymbol P_i = [X_i, Y_i, Z_i]^T Pi=[Xi,Yi,Zi]T ,它的投影坐标为 u i = [ u i , v i ] T \boldsymbol u_i = [u_i, v_i]^T ui=[ui,vi]T ;
用矩阵形式写出像素位置与空间点公式(理论上成立的等式(没有误差时)):
s i [ u i v i 1 ] = K e x p ( ξ ˆ ) [ X i Y i Z i 1 ] ( 1 ) ⇓ 即 s i u i = K ⋅ e x p ( ξ ˆ ) ⋅ P i ( 2 ) ⇓ 构建最小二乘问题 ξ ∗ = a r g min ξ 1 2 ∑ i = 1 n ∥ u i − 1 s i K exp ( ξ ˆ ) P i ∥ 2 2 ( 3 ) s_i\begin{bmatrix}u_i\\v_i\\1\end{bmatrix} = Kexp(\xi\^{})\begin{bmatrix}X_i\\Y_i\\Z_i\\1\end{bmatrix} \qquad\qquad\qquad\qquad (1)\\\; \Downarrow即\qquad \qquad\qquad\qquad\qquad\\\; \\s_i\boldsymbol u_i = K\cdot exp(\xi\^{})\cdot P_i \qquad \qquad\qquad\qquad\qquad(2)\\\; \\\Downarrow 构建最小二乘问题\qquad \qquad\\\; \\\xi^* = arg\min\limits_\xi \frac{1}{2}\sum\limits_{i=1}^n\begin{Vmatrix}u_i- \frac{1}{s_i} K\exp(\xi\^{})P_i\end{Vmatrix}^2_2\qquad(3) si uivi1 =Kexp(ξˆ) XiYiZi1 (1)⇓即siui=K⋅exp(ξˆ)⋅Pi(2)⇓构建最小二乘问题ξ∗=argξmin21i=1∑n ui−si1Kexp(ξˆ)Pi 22(3)
在上式中:
- (3)中的 u i \boldsymbol u_i ui :投影位置(观测值---------------------------已知) (2D)
- (2)和(1)中的 u i \boldsymbol u_i ui:重投影位置(预测值-根据(1)式计算得到) (2D)
- P i \boldsymbol {P_i} Pi : 空间点位置(已知) (3D)
重投影误差:用3D和估计位姿投影得到的位置和观测得到的位置作差得到的。实际中利用很多点调整相机位姿使得这个值变小,但不会精确为0.
- 求解这个最小二乘问题,由之前的李代数左乘模型,非线性优化的知识(推理过程略,详见视觉SLAM14讲7.7.3),记变换到相机坐标系下的空间点坐标 P ′ \boldsymbol {P'} P′ 这里直接给结果:

这个雅克比矩阵描述了重投影误差关于相机位姿李代数的一阶变化关系 ( s e ( 3 ) 这里是平移在前,旋转在后,则如上市,否则前后三列互换 se(3)这里是平移在前,旋转在后,则如上市,否则前后三列互换 se(3)这里是平移在前,旋转在后,则如上市,否则前后三列互换)。
此外,还有 e e e 关于空间点 P P P 的导数:
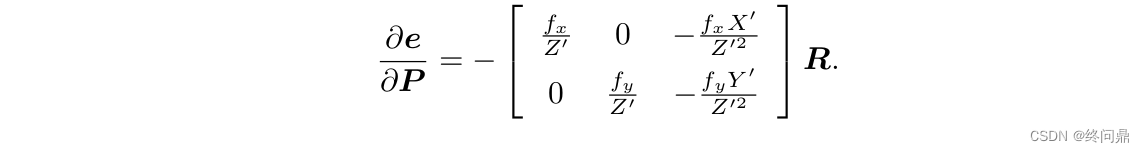
以上两个导数矩阵分别是观测相机方程关于相机位姿和特征点的导数矩阵。在优化中能提供迭代方向。
2. 3D-3D ICP
问题:有一组匹配好的3D点:
P = { p 1 , . . . , p n } , P ′ = { p 1 ′ , . . . , p n ′ } P=\left\{p_1, ..., p_n \right\}, \qquad P' = \left\{p'_1, ..., p'_n\right\} P={p1,...,pn},P′={p1′,...,pn′}
欲求一个欧式变换 R , t R,t R,t,使:
∀ i , p i = R p i ′ + t {\forall i}, \qquad p_i = Rp'_i + t ∀i,pi=Rpi′+t
用ICP(Iterative Closest Point)求解,没有出现相机模型,和相机无关,故激光SLAM中也有ICP。
2.1 代数法
2.1.1 SVD方法
定义误差:
e i = p i − ( R p i ′ + t ) e_i = p_i - (Rp'_i + t) ei=pi−(Rpi′+t)
构建最小二乘问题:使得误差平方和最小
min R , t J = 1 2 ∑ i = 1 n ∣ ∣ p i − ( R p i ′ + t ) ∣ ∣ 2 2 \min\limits_{R,t} J = \frac{1}{2}\sum\limits_{i=1}^n||p_i-(Rp'_i+t)||_2^2 R,tminJ=21i=1∑n∣∣pi−(Rpi′+t)∣∣22
求解问题:
- 定义两组点质心
p = 1 n ∑ i = 1 n ( p i ) , p ′ = 1 n ∑ i = 1 n ( p i ′ ) p=\frac{1}{n}\sum\limits_{i=1}^n(p_i),\qquad p'=\frac{1}{n}\sum\limits_{i=1}^n(p'_i) p=n1i=1∑n(pi),p′=n1i=1∑n(pi′) - 带入上边误差最小二乘函数整理,优化后结果:
min R , t J = 1 2 ∑ i = 1 n ∣ ∣ p i − p − R ( p i ′ − p ′ ) ∣ ∣ 2 + ∣ ∣ p − R p ′ − t ∣ ∣ 2 \min\limits_{R,t}J = \frac{1}{2}\sum\limits_{i=1}^n||p_i-p-R(p'_i-p')||^2+||p-Rp'-t||^2 R,tminJ=21i=1∑n∣∣pi−p−R(pi′−p′)∣∣2+∣∣p−Rp′−t∣∣2
观察,左边只和R有关,右边只和质心有关,有R时,令右边等于0,t可得。接下来着重求R - 展开上式中关于 R R R 平方项,定义一个 W W W,最终用SVD分解可得R,得到后求解t即可。
R = U V T R=UV^T R=UVT
2.2 优化(BA)法
2.2.2 非线性优化方法
和前边介绍的一样,构建G2O,然后导数用李代数扰动模型即可。
min ξ = 1 2 ∑ i = 1 n ∣ ∣ ( p i − e x p ( ξ \qquad\qquad\qquad\qquad\qquad\qquad\min\limits_\xi = \frac{1}{2}\sum\limits_{i=1}^n||(p_i-exp(\xi ξmin=21i=1∑n∣∣(pi−exp(ξ^ ) p i ′ ) ∣ ∣ 2 2 )\;p'_i)||^2_2 )pi′)∣∣22
注意:在唯一解的情况下,只要我们能找到极小值解,那么该值就是全局最优解。意味着可以任意选取初始值
相关文章:
【视觉SLAM入门】5.2. 2D-3D PNP 3D-3D ICP BA非线性优化方法 数学方法SVD DLT
"养气之学,戒之躁急" 1. 3D-2D PNP1.1 代数法1.1.1 DLT(直接线性变换法)1.1.2. P3P 1.2 优化法BA (Bundle Adjustment)法 2. 3D-3D ICP2.1 代数法2.1.1 SVD方法 2.2 优化(BA)法2.2.2 非线性优化方法 前置事项: 1. 3D-2D PNP 该问题描述为&am…...

人脸老化预测(Python)
本次项目的文件 main.py主程序如下 导入必要的库和模块: 导入 TensorFlow 库以及自定义的 FaceAging 模块。导入操作系统库和参数解析库。 定义 str2bool 函数: 自定义函数用于将字符串转换为布尔值。 创建命令行参数解析器: 使用 argparse.A…...
AWS SDK 3.x for .NET Framework 4.0 可行性测试
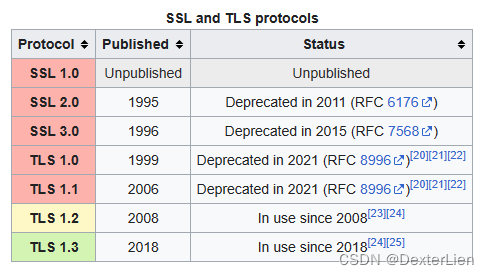
前言 为了应对日益增长的网络安全挑战, 越来越多的互联网厂商已经陆续开始或者已经彻底停止了对 SSL 3 / TLS 1.0 / TLS1.1 等上古加密算法的支持. 而对于一些同样拥有悠久历史的和 AWS 服务相关联的应用程序, 是否可以通过仅更新 SDK 版本的方式来适应新的环境. 本文将以 Win…...

两个list。如何使用流的写法将一个list中的对象中的某些属性根据另外一个list中的属性值赋值进去?
两个list。如何使用流的写法将一个list中的对象中的某些属性根据另外一个list中的属性值赋值进去? 你可以使用Java 8以上版本中的流(Stream)和Lambda表达式来实现这个需求。假设有两个List,一个是sourceList,包含要赋值属性的对象;另一个是…...

美国陆军希望大数据技术能够帮助保护其云安全
随着陆军采用更大型的云服务,一位高级官员警告说,一些在私营部门有效的快速软件开发技巧和简单解决方案(例如开放代码库)如果没有额外的安全性,将无法为军队工作。 我们知道现代软件开发确实依赖于第三方库ÿ…...

vue 文字跑马灯
<template><div class"marquee-container"><div class"marquee-content"><div>{{ marqueeText }}</div><div>{{ marqueeText }}</div> <!-- 复制一份文本,用于无缝衔接 --></div></d…...
开源ChatGPT系统源码 采用NUXT3+Laravel9后端开发 前后端分离版本
开源ChatGPT系统源码 采用NUXT3Laravel9后端开发 前后端分离版本 ChatGPT是一种基于AI的聊天机器人技术,它可以帮助用户与聊天机器人进行自然语言交流,以解决用户的问题或满足用户的需求。ChatGPT的核心技术是使用自然语言处理(NLPÿ…...

【LeetCode|数据结构】剑指 Offer 33. 二叉搜索树的后序遍历序列
题目链接 剑指 Offer 33. 二叉搜索树的后序遍历序列 标签 二叉搜索树、后序遍历 步骤 二叉搜索树的左子树的节点值 ≤ \le ≤根节点值 ≤ \le ≤右子树的节点值;对于后序遍历序列最后一个元素的值为根节点的值; 由上面的两个性质可以得出ÿ…...

自定义协程
难点 自己写了一遍协程,困难的地方在于unity中的执行顺序突然发现unity里面可以 yield return 的其实有很多 WaitForSeconds WaitForSecondsRealtime WaitForEndOfFrame WaitForFixedUpdate WaitUntil WaitWhile IEnumerator(可以用于协程嵌套…...

【Atcoder】 [ABC240Ex] Sequence of Substrings
题目链接 Atcoder方向 Luogu方向 题目解法 先考虑一个性质,选出的子串长度不会超过 2 n \sqrt {2n} 2n 考虑最劣的选法是选出长度为 1 , 2 , 3 , . . . 1,2,3,... 1,2,3,... 的子串(如果后一个选出的串比前一个子串长度大超过1,那么后…...
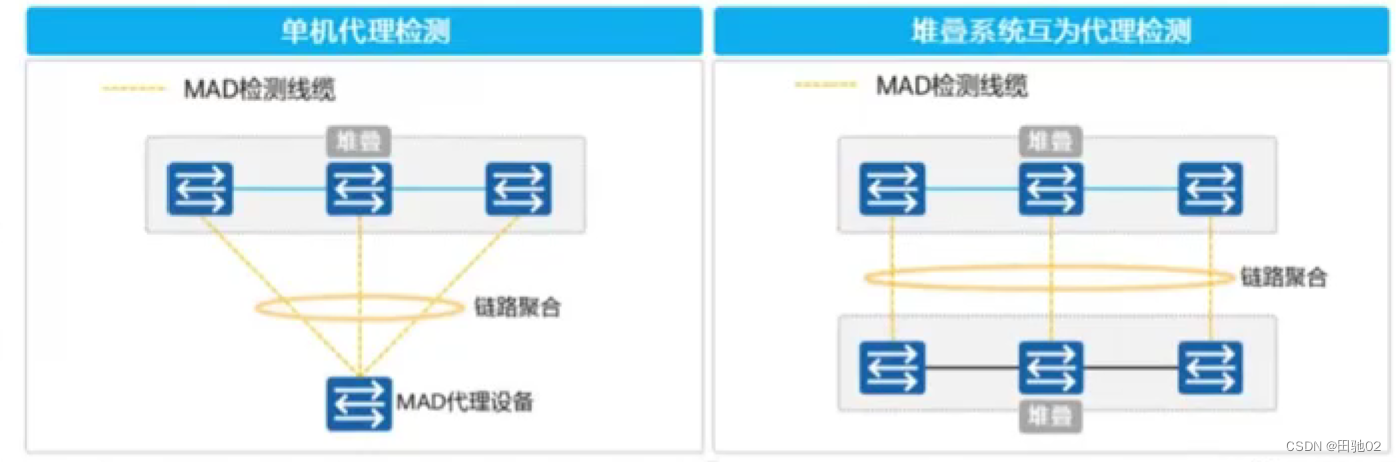
真机二阶段之堆叠技术
堆叠技术 --- 可以将多台真实的物理设备逻辑上抽象成一台 思科 -- VPC 华为 -- iStack和CSS 华三 -- IRF 锐捷 -- VSU iStack和CSS的区别: CSS --- 集群 --- 它仅支持将两台支持集群的交换机逻辑上整合成一台设备。 iStack --- 堆叠 --- 可以将多台支持堆叠的交换…...
简单、快速、无需注册的在线 MockJs 工具
简单、快速、无需注册的 MockJs 工具。通过参数来返回数据,传入什么参数就返回什么数据。 使用 接口只支持返回文本类数据,不支持图片、流数据等。 json 调用接口 https://mock.starxg.com/?responseBody{“say”:“hello”}&contentTypeapplic…...

【Linux取经路】探索进程状态之僵尸进程 | 孤儿进程
文章目录 一、进程状态概述1.1 运行状态详解1.2 阻塞状态详解1.3 挂起状态详解 二、具体的Linux操作系统中的进程状态2.1 Linux内核源代码2.2 查看进程状态2.3 D磁盘休眠状态(Disk sleep)2.4 T停止状态(stopped) 三、僵尸进程3.1 僵尸进程危害总结 四、孤儿进程五、结语 一、进…...

第十二章MyBatis动态SQL
if标签与where标签 if标签 test如果为true就会拼接查询条件,否则不会 当没有使用Param,test出现arg0/param1当使用Param,test为Param指定的值当使用Pojo,test为对象的属性名 select * from car where <if test"name!n…...

redis--发布订阅
redis的发布和订阅 在Redis中,发布-订阅(Publish-Subscribe,简称Pub/Sub)是一种消息传递模式,用于在不同的客户端之间传递消息,允许一个消息发布者将消息发送给多个订阅者。这种模式适用于解耦消息发送者和…...

链表2-两两交换链表中的节点删除链表的倒数第N个节点链表相交环形链表II
今天记录的题目: ● 24. 两两交换链表中的节点 ● 19.删除链表的倒数第N个节点 ● 面试题 02.07. 链表相交 ● 142.环形链表II 两两交换链表中的节点 题目链接:24. 两两交换链表中的节点 这题比较简单,记录好两个节点,交换其nex…...

数据结构之并查集
并查集 1. 并查集原理2. 并查集实现3. 并查集应用3.1 省份数量3.2 等式方程的可满足性 4. 并查集的优缺点及时间复杂度 1. 并查集原理 并查表原理是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。并查集的思想是用一个数组表示了整片森林࿰…...

[element-ui] el-date-picker a-range-picker type=“daterange“ rules 校验
项目场景: 在项目中表单提交有时间区间校验 问题描述 想当然的就和其他单个输入框字符串校验,导致提交保存的时候 ,初次日期未选择,规则提示。后续在同一表单上继续提交时,校验失效。走进了死胡同,一直以…...
Dockers搭建个人网盘、私有仓库,Dockerfile制作Nginx、Lamp镜像
目录 1、使用mysql:5.6和 owncloud 镜像,构建一个个人网盘。 (1)下载mysql:5.6和owncloud镜像 (2)创建启动mysql:5.6和owncloud容器 (3)在浏览器中输入网盘服务器的IP地址,进行账…...
)
2023 CCPC 华为云计算挑战赛 hdu7401 流量监控(树形dp)
题目 流量监控 - HDU 7401 - Virtual Judge 简单来说,T(T<20)组样例,sumn不超过2e4 每次给定一棵n(n<2000)个点的树,两问: ①将n个点恰拆成n/2个pair(u,v),要求一个点是另一个点的祖先,求方案数 …...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
