AVL树的讲解
算法拾遗三十八AVL树
- AVL树
- AVL树平衡性
- AVL树加入节点
- AVL删除节点
- AVL树代码
AVL树
AVL树具有最严苛的平衡性,(增、删、改、查)时间复杂度为O(logN),AVL树任何一个节点,左树的高度和右树的高度差不超过1(<2)
和SB树,红黑树时间复杂度一样,只是不同的人搞出了不同的平衡性。
AVL树就是一颗搜索二叉树和搜索二叉树的区别主要是做完属于搜索二叉树的调整之后有专属于自己平衡性的补丁。
搜索二叉树加节点,则小于根节点的挂左边,大于根节点的挂右边
搜索二叉树删除节点分情况:
1、当找到了要删除的节点X之后,X既没有左子树也没有右子树,则直接删除
2、找到了要删除的节点X之后,X有左但无右,那么直接让这个删除节点的X的左子树完全替代X
3、如果要删除的节点X,X无左有右,那么直接让右子树替代X
4、如果要删除的X既有左又有右,可以找左树的最右节点(最大节点)或者右树的最左节点(最小节点)代替X
AVL树平衡性
破坏平衡性操作:
LL:

需要调整为如下:

LR:
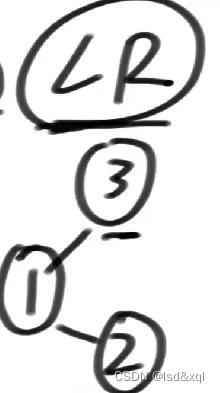
同理还有RR和RL型违规破坏平衡性。
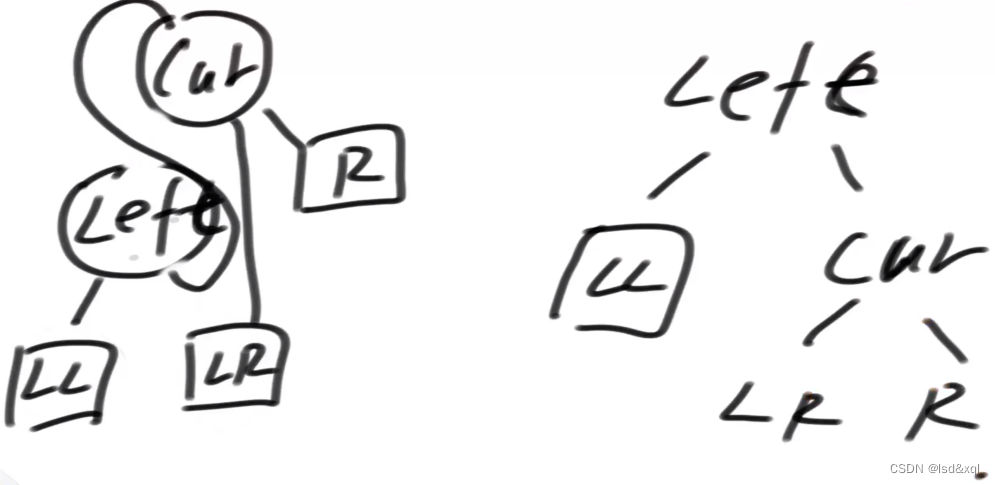
如下图(LR型违规:只要是LR型违规。则让那个孙节点跑上去保持平衡):
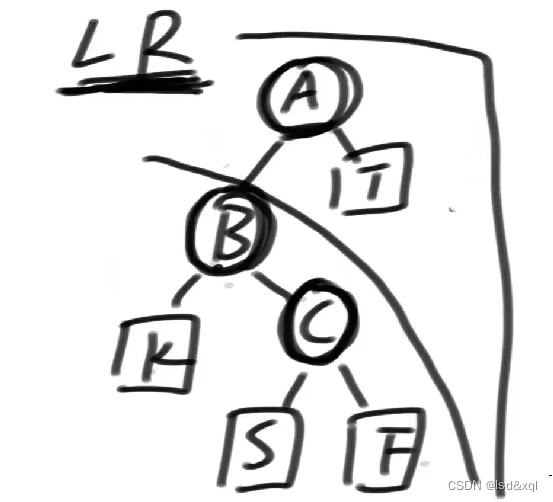
可知树的不平衡原因为:B的右子树导致的整棵树不平衡,则需要让C来到A节点的位置,那么需要在BC这棵树上对B来一个左旋,得到下图结果:
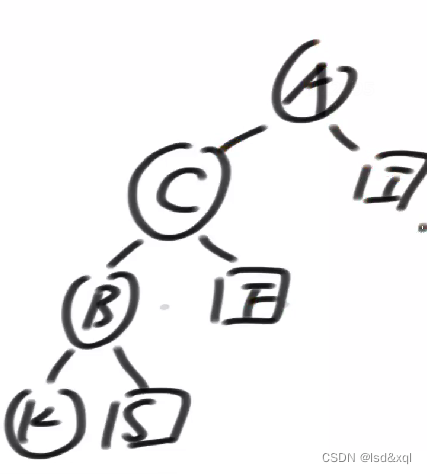
然后再对A来一个右旋C就上去了:
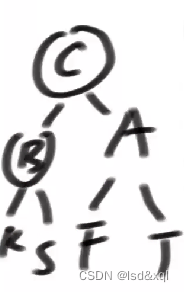
RL型违规:
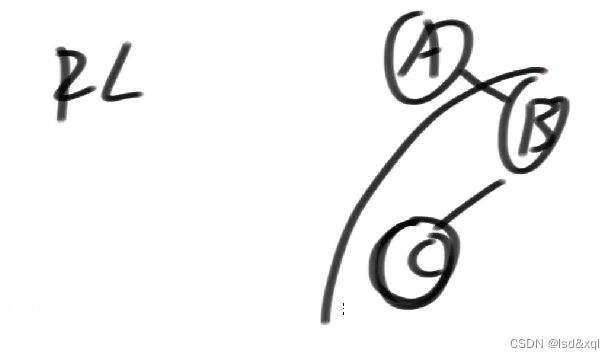
则让它的孙子节点顶上来就完事了,先在B上面执行一个右旋,让C顶上来,再在整棵树上执行一个A的左旋那么最后的C就上来了。
有一个细节:
有没有可能既是LL型违规又是LR型违规:
一棵树的左子树对应的左子树高度和这棵树的右子树对应的右子树高度一样所造成的不平衡是LL和LR型违规

如上图假设平衡二叉树左树高度为7右树高度为6,在某个时间右树删除一个数导致右树高度为5了,B的左树和右树高度都是6,我的失误既来自LL型又来自LR型
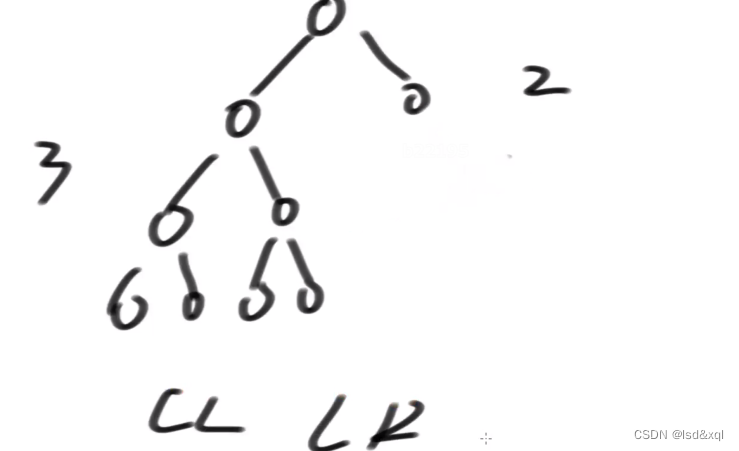
此时一定要按照LL型来调整,直接右旋(总能保证有效)。
如果用LR的方式来调整,则可能不对:有如下图
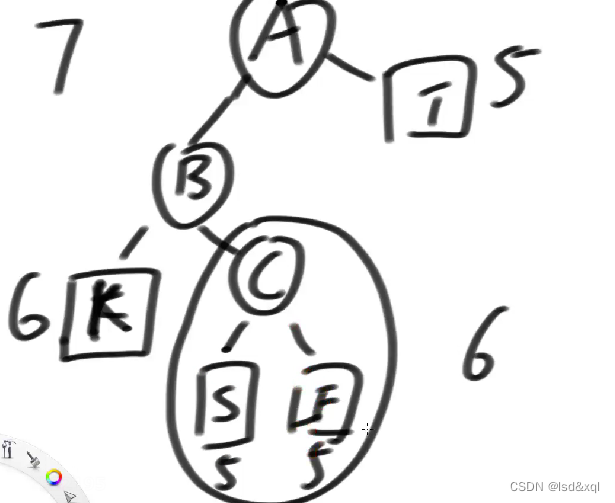
A的左树高度是7A的右树高度为5,如果这个例子按照LL型调整:会发现这棵树的高度是异常平衡的
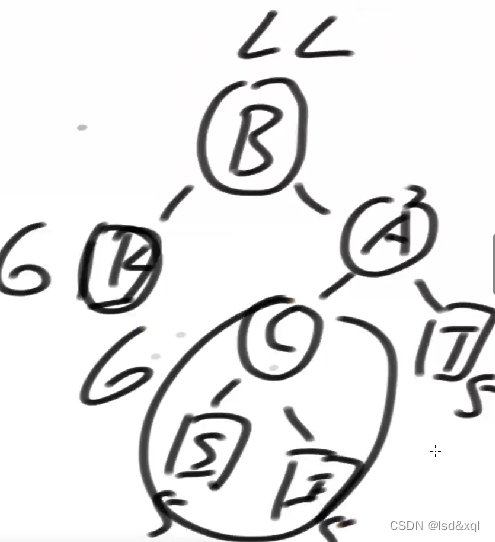
如果按照LR方式来调整:如果将S的高度调整成4的话
这样调整出来的K,S则不平了
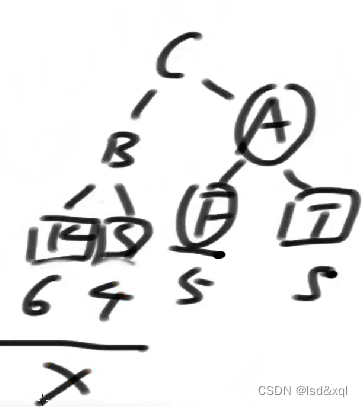
再来一个不平衡的:
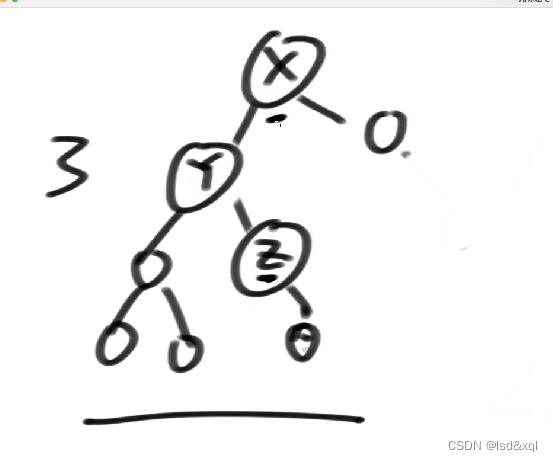
按照LR方式进行调整,z替代y的位置
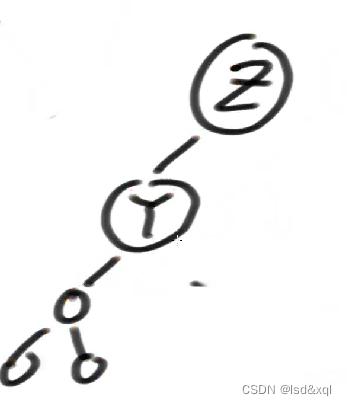
y接受了z的左空子树,y的右边是没有东西的,最后调整成这样:

综上:
总结:LL型违规只用进行一次右旋,LR型违规则需要进行一次小范围的左旋,再执行整棵树的右旋,RL型违规则需要先进行小范围上的右旋,再进行整棵树的左旋,RR型只需要进行一次左旋,时间复杂度均为O(1)
AVL树加入节点
加入一个节点之后需要依次查询加入的节点中了哪种类型的违规,如果未找到违规则找其对应的父节点,如果父节点未违规则继续找父节点对应的父节点,一直找到根节点未违规为止。
所以AVL树调整不是只对一个节点查是沿途所有节点都需要查(防止旋转一次后其上的节点还需要旋转),整体时间复杂度为O(logN)的调整代价,
如下图加入一个节点X首先看当前X节点是平的,再看X对应的父节点也是平的,最终找到方框标记的节点发现不再平衡了,左树高度为1,右树高度为3,而且是RR型违规
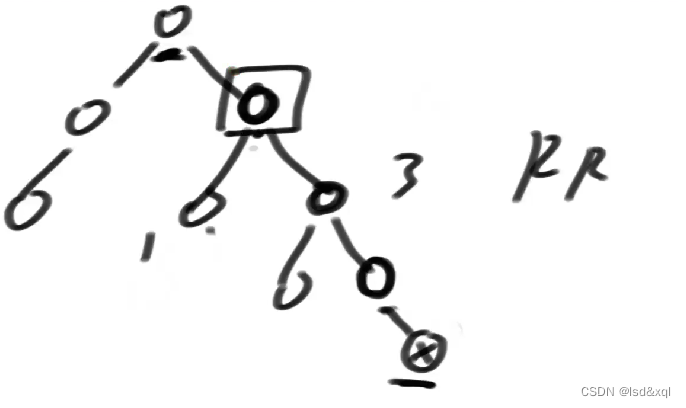
则需要进行左旋

AVL删除节点
分为以下情况:
1、X节点既没有左也没有右子树,这种情况只需要从删除节点开始算上面每一个父都要全查一遍。
2、X节点有右无左,直接拿右孩子替换原来的X,然后从右孩子来到的位置往上查询一遍
3、X节点既有左又有右孩子,看如下例子
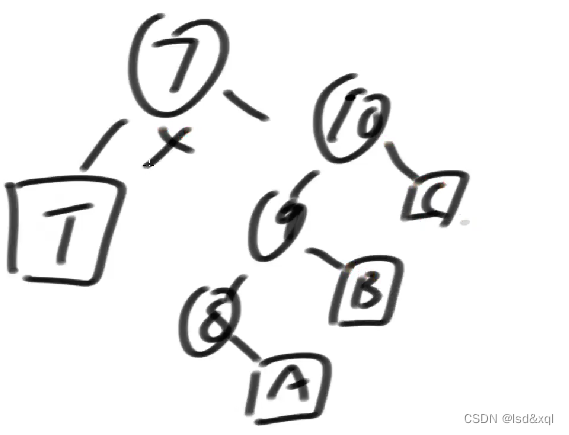
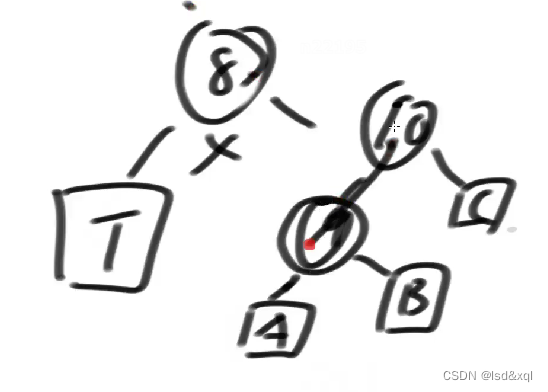
如果此处要删掉7,则需要找到7对应右孩子的最小值8去替换7的位置,调整成如下图的样子,此时只需要从9开始查它的父节点依次调整即可,
AVL树代码
右旋步骤:
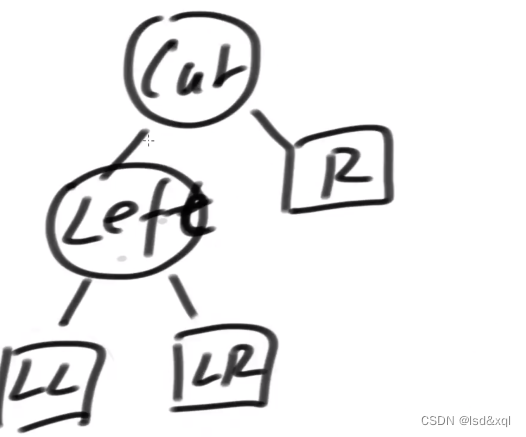
1、当前树的左边去接管左孩子的右
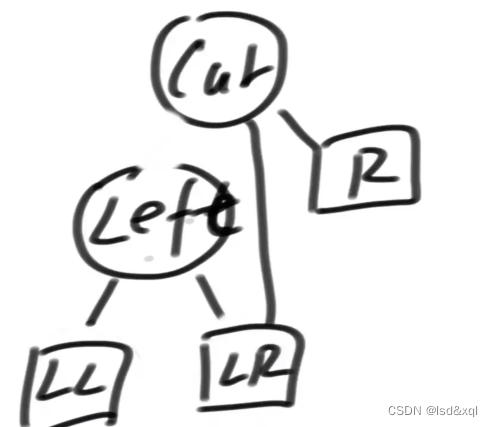
2、左孩子的右会接管cur
参照代码:
//右旋private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {//记录左孩子AVLNode<K, V> left = cur.l;//左孩子的右树挂载当前树的左边cur.l = left.r;//左孩子的右接管curleft.r = cur;//高度也得接管(现在左孩子和右孩子的高度最大的那个再加1)cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;left.h = Math.max((left.l != null ? left.l.h : 0), (left.r != null ? left.r.h : 0)) + 1;//右旋以left做头节点返回return left;}
再看AVL树add节点:
当前来到cur节点,要加的key是啥要加的value是啥,搜索二叉树潜台词为加入的key都不一样
public class Code_AVLTreeMap {public static class AVLNode<K extends Comparable<K>, V> {public K k;public V v;//左孩子及右孩子public AVLNode<K, V> l;public AVLNode<K, V> r;//高度public int h;public AVLNode(K key, V value) {k = key;v = value;h = 1;}}public static class AVLTreeMap<K extends Comparable<K>, V> {//根节点private AVLNode<K, V> root;//一共加入多少个节点private int size;public AVLTreeMap() {root = null;size = 0;}//右旋private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {//记录左孩子AVLNode<K, V> left = cur.l;//左孩子的右树挂载当前树的左边cur.l = left.r;//左孩子的右接管curleft.r = cur;//高度也得接管(现在左孩子和右孩子的高度最大的那个再加1)cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;left.h = Math.max((left.l != null ? left.l.h : 0), (left.r != null ? left.r.h : 0)) + 1;//右旋以left做头节点返回return left;}//左旋private AVLNode<K, V> leftRotate(AVLNode<K, V> cur) {AVLNode<K, V> right = cur.r;cur.r = right.l;right.l = cur;cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;right.h = Math.max((right.l != null ? right.l.h : 0), (right.r != null ? right.r.h : 0)) + 1;return right;}//平衡性调整private AVLNode<K, V> maintain(AVLNode<K, V> cur) {if (cur == null) {return null;}int leftHeight = cur.l != null ? cur.l.h : 0;int rightHeight = cur.r != null ? cur.r.h : 0;//此时左右树高度差大于1不平衡了if (Math.abs(leftHeight - rightHeight) > 1) {//左树高还是右树高if (leftHeight > rightHeight) {//左树高int leftLeftHeight = cur.l != null && cur.l.l != null ? cur.l.l.h : 0;int leftRightHeight = cur.l != null && cur.l.r != null ? cur.l.r.h : 0;//左树的左树高度大于等于右树的右树高度则LL型if (leftLeftHeight >= leftRightHeight) {//LL型违规cur = rightRotate(cur);} else {//LR型违规cur.l = leftRotate(cur.l);cur = rightRotate(cur);}} else {int rightLeftHeight = cur.r != null && cur.r.l != null ? cur.r.l.h : 0;int rightRightHeight = cur.r != null && cur.r.r != null ? cur.r.r.h : 0;if (rightRightHeight >= rightLeftHeight) {//RRcur = leftRotate(cur);} else {//RLcur.r = rightRotate(cur.r);cur = leftRotate(cur);}}}return cur;}private AVLNode<K, V> findLastIndex(K key) {AVLNode<K, V> pre = root;AVLNode<K, V> cur = root;while (cur != null) {pre = cur;if (key.compareTo(cur.k) == 0) {break;} else if (key.compareTo(cur.k) < 0) {cur = cur.l;} else {cur = cur.r;}}return pre;}private AVLNode<K, V> findLastNoSmallIndex(K key) {AVLNode<K, V> ans = null;AVLNode<K, V> cur = root;while (cur != null) {if (key.compareTo(cur.k) == 0) {ans = cur;break;} else if (key.compareTo(cur.k) < 0) {ans = cur;cur = cur.l;} else {cur = cur.r;}}return ans;}private AVLNode<K, V> findLastNoBigIndex(K key) {AVLNode<K, V> ans = null;AVLNode<K, V> cur = root;while (cur != null) {if (key.compareTo(cur.k) == 0) {ans = cur;break;} else if (key.compareTo(cur.k) < 0) {cur = cur.l;} else {ans = cur;cur = cur.r;}}return ans;}//AVL树加节点private AVLNode<K, V> add(AVLNode<K, V> cur, K key, V value) {if (cur == null) {//如果当前树为null,则新建节点return new AVLNode<K, V>(key, value);} else {//如果key小于当前树的kif (key.compareTo(cur.k) < 0) {//我去左树上面找,头部调整为当前节点的左树//之所以用cur.l = xxx 是因为这条记录挂在左树上是可能换头的//需要将返回值由我的头指针的左子树重新指一下接住cur.l = add(cur.l, key, value);} else {//右树上挂cur.r = add(cur.r, key, value);}//我自己的高度调整对cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;//做平衡调整return maintain(cur);}}// 在cur这棵树上,删掉key所代表的节点// 返回cur这棵树的新头部private AVLNode<K, V> delete(AVLNode<K, V> cur, K key) {if (key.compareTo(cur.k) > 0) {cur.r = delete(cur.r, key);} else if (key.compareTo(cur.k) < 0) {cur.l = delete(cur.l, key);} else {if (cur.l == null && cur.r == null) {cur = null;} else if (cur.l == null && cur.r != null) {cur = cur.r;} else if (cur.l != null && cur.r == null) {cur = cur.l;} else {AVLNode<K, V> des = cur.r;while (des.l != null) {des = des.l;}//调用右树删除整个k,同时调整了平衡cur.r = delete(cur.r, des.k);des.l = cur.l;des.r = cur.r;cur = des;}}if (cur != null) {cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;}return maintain(cur);}public int size() {return size;}public boolean containsKey(K key) {if (key == null) {return false;}AVLNode<K, V> lastNode = findLastIndex(key);return lastNode != null && key.compareTo(lastNode.k) == 0 ? true : false;}public void put(K key, V value) {if (key == null) {return;}AVLNode<K, V> lastNode = findLastIndex(key);if (lastNode != null && key.compareTo(lastNode.k) == 0) {lastNode.v = value;} else {size++;root = add(root, key, value);}}public void remove(K key) {if (key == null) {return;}if (containsKey(key)) {size--;root = delete(root, key);}}public V get(K key) {if (key == null) {return null;}AVLNode<K, V> lastNode = findLastIndex(key);if (lastNode != null && key.compareTo(lastNode.k) == 0) {return lastNode.v;}return null;}public K firstKey() {if (root == null) {return null;}AVLNode<K, V> cur = root;while (cur.l != null) {cur = cur.l;}return cur.k;}public K lastKey() {if (root == null) {return null;}AVLNode<K, V> cur = root;while (cur.r != null) {cur = cur.r;}return cur.k;}public K floorKey(K key) {if (key == null) {return null;}AVLNode<K, V> lastNoBigNode = findLastNoBigIndex(key);return lastNoBigNode == null ? null : lastNoBigNode.k;}public K ceilingKey(K key) {if (key == null) {return null;}AVLNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);return lastNoSmallNode == null ? null : lastNoSmallNode.k;}}}
相关文章:

AVL树的讲解
算法拾遗三十八AVL树 AVL树AVL树平衡性AVL树加入节点AVL删除节点AVL树代码 AVL树 AVL树具有最严苛的平衡性,(增、删、改、查)时间复杂度为O(logN),AVL树任何一个节点,左树的高度和右树的高度差…...

Unity 之 Input类
文章目录 总述具体介绍 总述 Input 类是 Unity 中用于处理用户输入的重要工具,它允许您获取来自键盘、鼠标、触摸屏和控制器等设备的输入数据。通过 Input 类,您可以轻松地检测按键、鼠标点击、鼠标移动、触摸、控制器按钮等用户输入事件。以下是关于 I…...
亚信科技AntDB数据库连年入选《中国DBMS市场指南》代表厂商
近日,全球权威ICT研究与顾问咨询公司Gartner发布了2023年《Market Guide for DBMS, China》(即“中国DBMS市场指南”),该指南从市场份额、技术创新、研发投入等维度对DBMS供应商进行了调研。亚信科技是领先的数智化全栈能力提供商…...
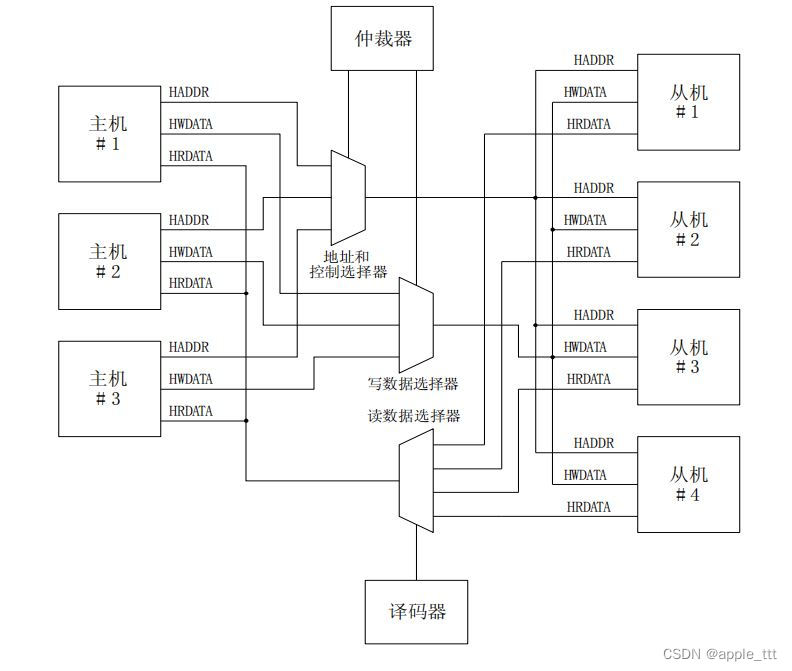
AMBA总线协议(3)——AHB(一)
目录 一、前言 二、什么是AHB总线 1、概述 2、一个典型的基于AHB总线的微处理器架构 3、基本的 AHB 传送特性 三、AMBA AHB总线互联 四、小结 一、前言 在之前的文章中我们初步的了解了一下AMBA总线中AHB,APB,AXI的信号线及其功能,从本文开始我们…...

Git commit与pull的先后顺序
Git commit与pull的先后顺序_git先pull再commit_Mordor Java Girl的博客-CSDN博客 编辑yucoang2020.04.21 回复 28 先pull再commit的话, 你的commit也就不再纯粹了. 这一个commit不再是"你所编辑的xxx功能, 而是"别人所编辑的你所编辑的xxx". 我认为提交历…...
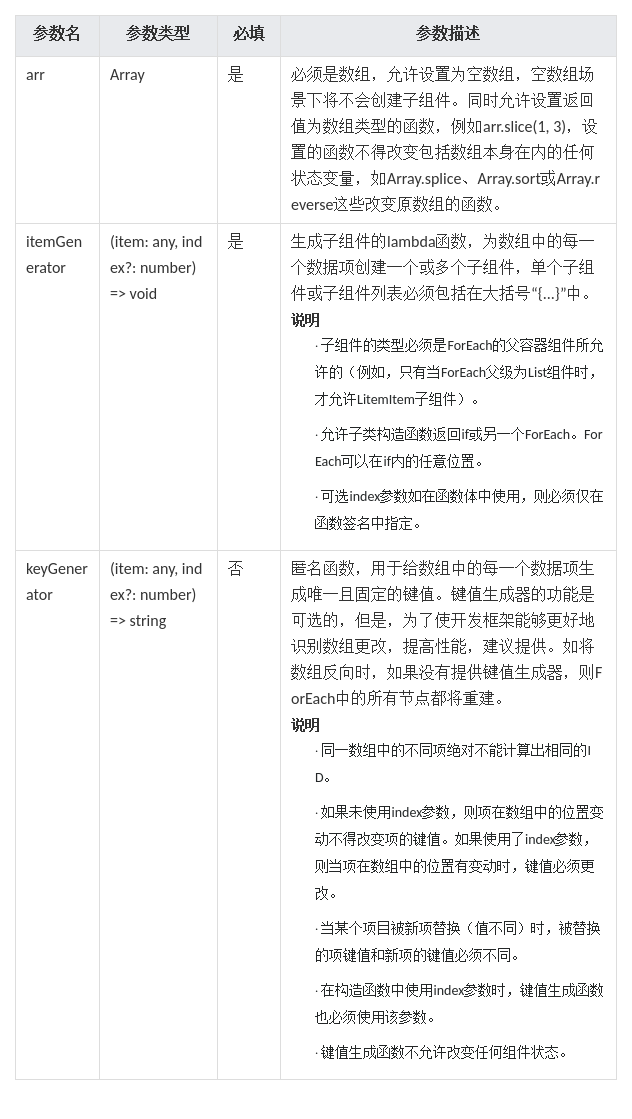
HarmonyOS/OpenHarmony应用开发-ArkTS语言渲染控制ForEach循环渲染
ForEach基于数组类型数据执行循环渲染。说明,从API version 9开始,该接口支持在ArkTS卡片中使用。 一、接口描述 ForEach(arr: any[], itemGenerator: (item: any, index?: number) > void,keyGenerator?: (item: any, index?: number) > stri…...

Powered by Paraverse | 平行云助力彼真科技打造演出“新物种”
01 怎么看待虚拟演出 彼真科技 我们怎么看待虚拟演出? 虚拟演出给音乐人或者音乐行业带来了哪些新的机会?通过呈现一场高标准的虚拟演出,我们的能力延伸点在哪里? 先说一下我们认知里的虚拟演出的本质: 音乐演出是一…...
企微配置回调服务
1、企微配置可信域名 2、企微获取成员userID 3、企微获取用户敏感数据 4、企微配置回调服务 文章目录 一、简介1、概述2、相关文档地址 二、企微配置消息服务器1、配置消息接收参数2、参数解析3、参数拼接规则 三、代码编写—使用已有库1、代码下载2、代码修改3、服务代码编写 …...

机器人远程控制软件设计
机器人远程控制软件设计 That’s all....
:React中的虚拟DOM是什么?)
面试题-React(二):React中的虚拟DOM是什么?
一、什么是虚拟DOM? 虚拟DOM是React的核心概念之一,它是一个轻量级的JavaScript对象树,用于表示真实DOM的状态。在React中,当数据发生变化时,首先会在虚拟DOM上执行DOM更新,而不是直接操作真实DOM。然后&a…...

分布式链路追踪——Dapper, a Large-Scale Distributed Systems Tracing Infrastructure
要解决的问题 如何记录请求经过多个分布式服务的信息,以便分析问题所在?如何保证这些信息得到完整的追踪?如何尽可能不影响服务性能? 追踪 当用户请求到达前端A,将会发送rpc请求给中间层B、C;B可以立刻作…...

【IEEE会议】第二届IEEE云计算、大数据应用与软件工程国际学术会议 (CBASE2023)
第二届IEEE云计算、大数据应用与软件工程国际学术会议 (CBASE2023) 随着大数据时代的到来,对数据获取的随时性和对计算的需求也在逐渐增长。为推动大数据时代的云计算与软件工程的发展,促进该领域学术交流,在CBASE 2022成功举办的…...

Streamlit项目:基于讯飞星火认知大模型开发Web智能对话应用
文章目录 1 前言2 API获取3 官方文档的调用代码4 Streamlit 网页的搭建4.1 代码及效果展示4.2 Streamlit相关知识点 5 结语 1 前言 科大讯飞公司于2023年8月15日发布了讯飞认知大模型V2.0,这是一款集跨领域知识和语言理解能力于一体的新一代认知智能大模型。前日&a…...
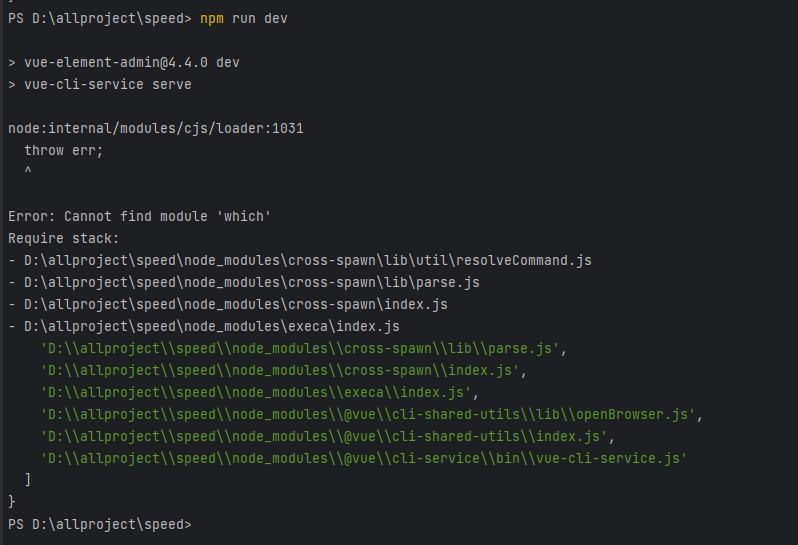
[Vue]解决npm run dev报错node:internal/modules/cjs/loader:1031 throw err;
解决: 有2中方法,建议先尝试第一种,不行再第二种 第一种: 重新安装依赖环境 删除项目的node_modules文件夹,重新执行 # 安装依赖环境 npm install# 运行 npm run dev 我只用了第一种方法就可以了 ,第二种方法从别的博主那看到…...
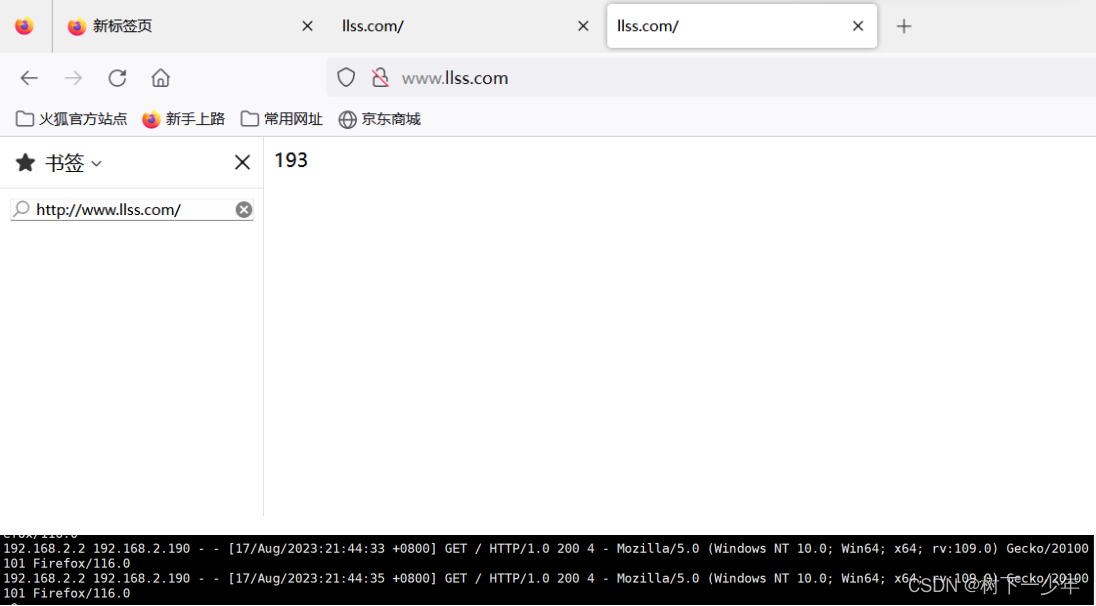
nginx反向代理后实现nginx和apache两种web服务器能够记录客户端的真实IP地址
一.构建环境 二.配置反向代理 1.基于源码安装的nginx环境下修改nginx.conf(设备1) 2.通过windows powershell进行修改hosts文件并测试 3.设备2和设备3上查看日志,可以看到访问来源都是代理服务器(2.190)而不是真实…...
【仿写tomcat】四、解析http请求信息,响应给前端,HttpServletRequest、HttpServletResponse的简单实现
思考 在解析请求之前我们要思考一个问题,我们解析的是其中的哪些内容? 对于最基本的实现,当然是请求类型,请求的url以及请求参数,我们可以根据请求的类型作出对应的处理,通过url在我们的mapstore中找到se…...

FL Studio21.1中文完整版Win/Mac
FL Studio All Plugins Edition【中文完整版 Win/Mac】适合音乐制作人/工作室使用,全套插件!(20.9新增Vintage Chorus,Pitch Shifter变调插件)FL Studio是超多顶级音乐人的启蒙首选!包括百大DJ冠军Martin Garrix&…...
基于Mysql+Vue+Django的协同过滤和内容推荐算法的智能音乐推荐系统——深度学习算法应用(含全部工程源码)+数据集
目录 前言总体设计系统整体结构图系统流程图 运行环境Python 环境MySQL环境VUE环境 模块实现1. 数据请求和储存2. 数据处理计算歌曲、歌手、用户相似度计算用户推荐集 3. 数据存储与后台4. 数据展示 系统测试工程源代码下载其它资料下载 前言 本项目以丰富的网易云音乐数据为基…...
Python Web开发 Django 简介
今天来为大家介绍 Python 另一个 Web 开发框架 Django,它是一个基于 Python 定制的开源 Web 应用框架,最早源于一个在线新闻 Web 网站,后于2005年开源。Django 的功能大而全,它提供的一站式解决的思路,能让开发者不用在…...

HAproxy搭建web集群
目录 一、HAproxy 概述 二、HAproxy 主要特性 三、HAproxy 负载均衡策略(八种) 四、LVS、Nginx、HAproxy区别 Nginx LVS HAproxy 五、HAproxy部署实战 问题总结: 一、HAproxy 概述 HAProxy是可提供高可用性、负载均衡以及基于TCP和HTTP应用的代理࿰…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
