大数据:NumPy进阶应用详解
专栏介绍
结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来!
全部文章请访问专栏:《Python全栈教程(0基础)》
再推荐一下最近热更的:《大厂测试高频面试题详解》 该专栏对近年高频测试相关面试题做详细解答,结合自己多年工作经验,以及同行大佬指导总结出来的。旨在帮助测试、python方面的同学,顺利通过面试,拿到自己满意的offer!
文章目录
- 专栏介绍
- NumPy进阶应用
- 数组的运算
- 数组跟标量的运算
- 数组跟数组的运算
- 通用一元函数
- 通用二元函数
- 广播机制
- 其他常用函数
- 矩阵运算
- 线性代数快速回顾
- NumPy中矩阵相关函数
- NumPy的线性代数模块
NumPy进阶应用
数组的运算
使用 NumPy 最为方便的是当需要对数组元素进行运算时,不用编写循环代码遍历每个元素,所有的运算都会自动的矢量化(使用高效的、提前编译的底层代码来对数据序列进行数学操作)。简单的说就是,NumPy 中的数学运算和数学函数会自动作用于数组中的每个成员。
数组跟标量的运算
代码:
array35 = np.arange(1, 10)
print(array35 + 10)
print(array35 * 10)
输出:
[11 12 13 14 15 16 17 18 19]
[10 20 30 40 50 60 70 80 90]
数组跟数组的运算
代码:
array36 = np.array([1, 1, 1, 2, 2, 2, 3, 3, 3])
print(array35 + array36)
print(array35 * array36)
print(array35 ** array36)
输出:
[ 2 3 4 6 7 8 10 11 12]
[ 1 2 3 8 10 12 21 24 27]
[ 1 2 3 16 25 36 343 512 729]
通用一元函数
通用函数是对ndarray中的数据执行元素级运算的函数。你可以将其看做普通函数(接收一个标量值作为参数,返回一个标量值)的矢量化包装器,如下所示。
代码:
print(np.sqrt(array35))
print(np.log2(array35))
输出:
[1. 1.41421356 1.73205081 2. 2.23606798 2.449489742.64575131 2.82842712 3. ]
[0. 1. 1.5849625 2. 2.32192809 2.58496252.80735492 3. 3.169925 ]
表1:通用一元函数
| 函数 | 说明 |
|---|---|
abs / fabs | 求绝对值的函数 |
sqrt | 求平方根的函数,相当于array ** 0.5 |
square | 求平方的函数,相当于array ** 2 |
exp | 计算 e x e^x ex的函数 |
log / log10 / log2 | 对数函数(e为底 / 10为底 / 2为底) |
sign | 符号函数(1 - 正数;0 - 零;-1 - 负数) |
ceil / floor | 上取整 / 下取整 |
isnan | 返回布尔数组,NaN对应True,非NaN对应False |
isfinite / isinf | 判断数值是否为无穷大的函数 |
cos / cosh / sin | 三角函数 |
sinh / tan / tanh | 三角函数 |
arccos / arccosh / arcsin | 反三角函数 |
arcsinh / arctan / arctanh | 反三角函数 |
rint / round | 四舍五入函数 |
通用二元函数
代码:
array37 = np.array([[4, 5, 6], [7, 8, 9]])
array38 = np.array([[1, 2, 3], [3, 2, 1]])
print(array37 ** array38)
print(np.power(array37, array38))
输出:
[[ 4 25 216][343 64 9]]
[[ 4 25 216][343 64 9]]
表2:通用二元函数
| 函数 | 说明 |
|---|---|
add(x, y) / substract(x, y) | 加法函数 / 减法函数 |
multiply(x, y) / divide(x, y) | 乘法函数 / 除法函数 |
floor_divide(x, y) / mod(x, y) | 整除函数 / 求模函数 |
allclose(x, y) | 检查数组x和y元素是否几乎相等 |
power(x, y) | 数组 x x x的元素 x i x_i xi和数组 y y y的元素 y i y_i yi,计算 x i y i x_i^{y_i} xiyi |
maximum(x, y) / fmax(x, y) | 两两比较元素获取最大值 / 获取最大值(忽略NaN) |
minimum(x, y) / fmin(x, y) | 两两比较元素获取最小值 / 获取最小值(忽略NaN) |
dot(x, y) | 点积运算(数量积,通常记为 ⋯ \cdots ⋯,用于欧几里得空间(Euclidean space)) |
inner(x, y) | 内积运算(内积的含义要高于点积,点积相当于是内积在欧几里得空间$$的特例,而内积可以推广到赋范向量空间,只要它满足平行四边形法则即可) |
cross(x, y) | 叉积运算(向量积,通常记为 × \times ×,运算结果是一个向量) |
outer(x, y) | 外积运算(张量积,通常记为 ⨂ \bigotimes ⨂,运算结果通常是一个矩阵) |
intersect1d(x, y) | 计算x和y的交集,返回这些元素构成的有序数组 |
union1d(x, y) | 计算x和y的并集,返回这些元素构成的有序数组 |
in1d(x, y) | 返回由判断x 的元素是否在y中得到的布尔值构成的数组 |
setdiff1d(x, y) | 计算x和y的差集,返回这些元素构成的数组 |
setxor1d(x, y) | 计算x和y的对称差,返回这些元素构成的数组 |
补充说明:在二维空间内,两个向量 A = [ a 1 a 2 ] \boldsymbol{A}=\begin{bmatrix} a_1 \\ a_2 \end{bmatrix} A=[a1a2]和 B = [ b 1 b 2 ] \boldsymbol{B}=\begin{bmatrix} b_1 \\ b_2 \end{bmatrix} B=[b1b2]的叉积是这样定义的: A × B = ∣ a 1 a 2 b 1 b 2 ∣ = a 1 b 2 − a 2 b 1 \boldsymbol{A}\times \boldsymbol{B}=\begin{vmatrix} a_1 \quad a_2 \\ b_1 \quad b_2 \end{vmatrix}=a_1b_2 - a_2b_1 A×B= a1a2b1b2 =a1b2−a2b1,其中 ∣ a 1 a 2 b 1 b 2 ∣ \begin{vmatrix} a_1 \quad a_2 \\ b_1 \quad b_2 \end{vmatrix} a1a2b1b2 称为行列式。但是一定要注意,叉积并不等同于行列式,行列式的运算结果是一个标量,而叉积运算的结果是一个向量。如果不明白,我们可以看看三维空间两个向量, A = [ a 1 a 2 a 3 ] \boldsymbol{A}=\begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} A= a1a2a3 和 B = [ b 1 b 2 b 3 ] \boldsymbol{B}=\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} B= b1b2b3 的叉积是 < i ^ ∣ a 2 a 3 b 2 b 3 ∣ , − j ^ ∣ a 1 a 3 b 1 b 3 ∣ , k ^ ∣ a 1 a 2 b 1 b 2 ∣ > \left< \hat{i} \begin{vmatrix} a_2 \quad a_3 \\ b_2 \quad b_3 \end{vmatrix}, -\hat{j} \begin{vmatrix} a_1 \quad a_3 \\ b_1 \quad b_3 \end{vmatrix}, \hat{k} \begin{vmatrix} a_1 \quad a_2 \\ b_1 \quad b_2 \end{vmatrix} \right> ⟨i^ a2a3b2b3 ,−j^ a1a3b1b3 ,k^ a1a2b1b2 ⟩,其中 i ^ , j ^ , k ^ \hat{i}, \hat{j}, \hat{k} i^,j^,k^代表每个维度的单位向量。
广播机制
上面的例子中,两个二元运算的数组形状是完全相同的,我们再来研究一下,两个形状不同的数组是否可以直接做二元运算或使用二元函数进行运算,请看下面的例子。
代码:
array39 = np.array([[0, 0, 0], [1, 1, 1], [2, 2, 2], [3, 3, 3]])
array40 = np.array([1, 2, 3])
array39 + array40
输出:
array([[1, 2, 3],[2, 3, 4],[3, 4, 5],[4, 5, 6]])
代码:
array41 = np.array([[1], [2], [3], [4]])
array39 + array41
输出:
array([[1, 1, 1],[3, 3, 3],[5, 5, 5],[7, 7, 7]])
通过上面的例子,我们发现形状不同的数组仍然有机会进行二元运算,但也绝对不是任意的数组都可以进行二元运算。简单的说,只有两个数组后缘维度相同或者其中一个数组后缘维度为1时,广播机制会被触发,而通过广播机制如果能够使两个数组的形状一致,才能进行二元运算。所谓后缘维度,指的是数组shape属性对应的元组中最后一个元素的值(从后往前数最后一个维度的值),例如,我们之前打开的图像对应的数组后缘维度为3,3行4列的二维数组后缘维度为4,而有5个元素的一维数组后缘维度为5。简单的说就是,后缘维度相同或者其中一个数组的后缘维度为1,就可以应用广播机制;而广播机制如果能够使得数组的形状一致,就满足了两个数组对应元素做运算的需求,如下图所示。
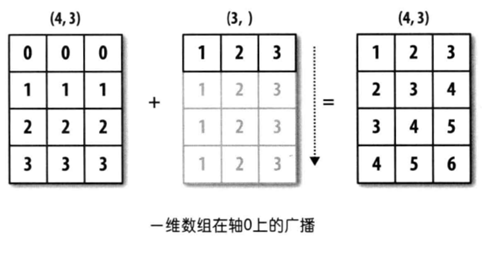
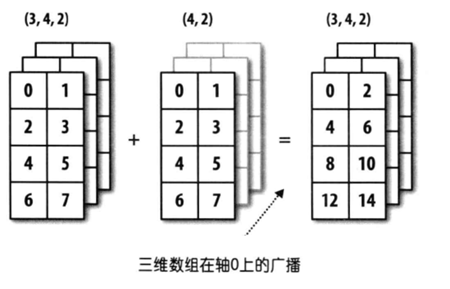
其他常用函数
除了上面讲到的函数外,NumPy 中还提供了很多用于处理数组的函数,ndarray对象的很多方法也可以通过直接调用函数来实现,下表给出了一些常用的函数。
表3:NumPy其他常用函数
| 函数 | 说明 |
|---|---|
unique | 去除数组重复元素,返回唯一元素构成的有序数组 |
copy | 返回拷贝数组得到的数组 |
sort | 返回数组元素排序后的拷贝 |
split / hsplit / vsplit | 将数组拆成若干个子数组 |
stack / hstack / vstack | 将多个数组堆叠成新数组 |
concatenate | 沿着指定的轴连接多个数组构成新数组 |
append / insert | 向数组末尾追加元素 / 在数组指定位置插入元素 |
argwhere | 找出数组中非0元素的位置 |
extract / select / where | 按照指定的条件从数组中抽取或处理数组元素 |
flip | 沿指定的轴翻转数组中的元素 |
fromiter | 通过迭代器创建数组对象 |
fromregex | 通过读取文件和正则表达式解析获取数据创建数组对象 |
repeat / tile | 通过对元素的重复来创建新数组 |
roll | 沿指定轴对数组元素进行移位 |
resize | 重新调整数组的大小 |
place / put | 将数组中满足条件的元素/指定的元素替换为指定的值 |
partition | 用选定的元素对数组进行一次划分并返回划分后的数组 |
提示:上面的
resize函数和ndarray对象的resize方法是有区别的,resize函数在调整数组大小时会重复数组中的元素作为填补多出来的元素的值,而ndarry对象的resize方法是用0来填补多出来的元素。这些小细节不清楚暂时也不要紧,但是如果用到对应的功能了就要引起注意。
代码:
array42 = np.array([[1, 1, 1], [2, 2, 2], [3, 3, 3]])
array43 = np.array([[4, 4, 4], [5, 5, 5], [6, 6, 6]])
np.hstack((array42, array43))
输出:
array([[1, 1, 1, 4, 4, 4],[2, 2, 2, 5, 5, 5],[3, 3, 3, 6, 6, 6]])
代码:
np.vstack((array42, array43))
输出:
array([[1, 1, 1],[2, 2, 2],[3, 3, 3],[4, 4, 4],[5, 5, 5],[6, 6, 6]])
代码:
np.concatenate((array42, array43))
输出:
array([[1, 1, 1],[2, 2, 2],[3, 3, 3],[4, 4, 4],[5, 5, 5],[6, 6, 6]])
代码:
np.concatenate((array42, array43), axis=1)
输出:
array([[1, 1, 1, 4, 4, 4],[2, 2, 2, 5, 5, 5],[3, 3, 3, 6, 6, 6]])
矩阵运算
NumPy 中提供了专门用于线性代数(linear algebra)的模块和表示矩阵的类型matrix,当然我们通过二维数组也可以表示一个矩阵,官方并不推荐使用matrix类而是建议使用二维数组,而且有可能在将来的版本中会移除matrix类。无论如何,利用这些已经封装好的类和函数,我们可以轻松愉快的实现线性代数中很多的操作。
线性代数快速回顾
- 向量也叫矢量,是一个同时具有大小和方向,且满足平行四边形法则的几何对象。与向量相对的概念叫标量或数量,标量只有大小、绝大多数情况下没有方向。
- 向量可以进行加、减、数乘、点积、叉积等运算。
- 行列式由向量组成,它的性质可以由向量解释。
- 行列式可以使用行列式公式计算: d e t ( A ) = ∑ n ! ± a 1 α a 2 β ⋯ a n ω det(\boldsymbol{A})=\sum_{n!} \pm {a_{1\alpha}a_{2\beta} \cdots a_{n\omega}} det(A)=∑n!±a1αa2β⋯anω。
- 高阶行列式可以用代数余子式展开成多个低阶行列式,如: d e t ( A ) = a 11 C 11 + a 12 C 12 + ⋯ + a 1 n C 1 n det(\boldsymbol{A})=a_{11}C_{11}+a_{12}C_{12}+ \cdots +a_{1n}C_{1n} det(A)=a11C11+a12C12+⋯+a1nC1n。
- 矩阵是由一系列元素排成的矩形阵列,矩阵里的元素可以是数字、符号或数学公式。
- 矩阵可以进行加法、减法、数乘、乘法、转置等运算。
- 逆矩阵用 A − 1 \boldsymbol{A^{-1}} A−1表示, A A − 1 = A − 1 A = I \boldsymbol{A}\boldsymbol{A^{-1}}=\boldsymbol{A^{-1}}\boldsymbol{A}=\boldsymbol{I} AA−1=A−1A=I;没有逆矩阵的方阵是奇异矩阵。
- 如果一个方阵是满秩矩阵(矩阵的秩等于矩阵的阶数),该方阵对应的线性方程有唯一解。
说明:矩阵的秩是指矩阵中线性无关的行/列向量的最大个数,同时也是矩阵对应的线性变换的像空间的维度。
NumPy中矩阵相关函数
-
创建矩阵对象。
代码:
# matrix构造函数可以传入类数组对象也可以传入字符串 m1 = np.matrix('1 2 3; 4 5 6') m1输出:
matrix([[1, 2, 3],[4, 5, 6]])代码:
# asmatrix函数也可以写成mat函数,它们其实是同一个函数 m2 = np.asmatrix(np.array([[1, 1], [2, 2], [3, 3]])) m2输出:
matrix([[1, 1],[2, 2],[3, 3]])代码:
m1 * m2输出:
matrix([[14, 14],[32, 32]])说明:注意
matrix对象和ndarray对象乘法运算的差别,如果两个二维数组要做矩阵乘法运算,应该使用@运算符或matmul函数,而不是*运算符。 -
矩阵对象的属性。
属性 说明 A获取矩阵对象对应的 ndarray对象A1获取矩阵对象对应的扁平化后的 ndarray对象I可逆矩阵的逆矩阵 T矩阵的转置 H矩阵的共轭转置 shape矩阵的形状 size矩阵元素的个数 -
矩阵对象的方法。
矩阵对象的方法跟之前讲过的ndarray数组对象的方法基本差不多,此处不再进行赘述。
NumPy的线性代数模块
NumPy 的linalg模块中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的函数,它们跟 MATLAB 和 R 等语言所使用的是相同的行业标准线性代数库,下面的表格列出了numpy以及linalg模块中常用的跟线性代数相关的函数。
| 函数 | 说明 |
|---|---|
diag | 以一维数组的形式返回方阵的对角线元素或将一维数组转换为方阵(非对角元素元素为0) |
vdot | 向量的点积 |
dot | 数组的点积 |
inner | 数组的内积 |
outer | 数组的叉积 |
trace | 计算对角线元素的和 |
norm | 求模(范数)运算 |
det | 计算行列式的值(在方阵上计算会得到一个标量) |
matrix_rank | 计算矩阵的秩 |
eig | 计算矩阵的特征值(eigenvalue)和特征向量(eigenvector) |
inv | 计算非奇异矩阵( n n n阶方阵)的逆矩阵 |
pinv | 计算矩阵的摩尔-彭若斯(Moore-Penrose)广义逆 |
qr | QR分解(把矩阵分解成一个正交矩阵与一个上三角矩阵的积) |
svd | 计算奇异值分解(singular value decomposition) |
solve | 解线性方程组 A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b,其中 A \boldsymbol{A} A是一个方阵 |
lstsq | 计算 A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b的最小二乘解 |
大家如果有兴趣可以用下面的代码验证上面的函数。
代码:
m3 = np.array([[1., 2.], [3., 4.]])
np.linalg.inv(m3)
输出:
array([[-2. , 1. ],[ 1.5, -0.5]])
代码:
m4 = np.array([[1, 3, 5], [2, 4, 6], [4, 7, 9]])
np.linalg.det(m4)
输出:
2
代码:
# 解线性方程组ax=b
# 3*x1 + x2= 9,x1 + 2*x2 = 8
a = np.array([[3,1], [1,2]])
b = np.array([9, 8])
np.linalg.solve(a, b)
输出:
array([2., 3.])
相关文章:

大数据:NumPy进阶应用详解
专栏介绍 结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来! 全部文章请访问专栏:《Python全栈教…...
new String创建几个对象
在java17中 : 问题1:new String("abc")会产生多少个对象? 分两种情况: 情况1: 如果”abc”这个字符串常量不存在,则创建两个对象,分别是“abc”这个字符串常量,以及ne…...
【路由协议】使用按需路由协议和数据包注入的即时网络模拟传递率(PDR)、总消耗能量和节点消耗能量以及延迟研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

c#实现依赖注入
当谈到C#中的依赖注入(Dependency Injection,DI)时,我们可以使用一个简单的示例来说明它是如何工作的。依赖注入是一种设计模式,用于将依赖关系从一个类传递到另一个类,以实现松耦合和可测试性。 假设我们有一个简单的订单处理应用程序,其中包含两个主要类:OrderServi…...

算法通关村十一关 | 位运算实现加法和乘法
1.位实现加法和乘法 在计算机中,位运算的效率要比加减乘除的效率更高,因此在高性能软件中源码中大量使用,计算机里各种运算基本上都是位运算。 学习下面内容之前建议先学习位运算规则:算法通关村十一关 | 位运算的规则_我爱学算…...
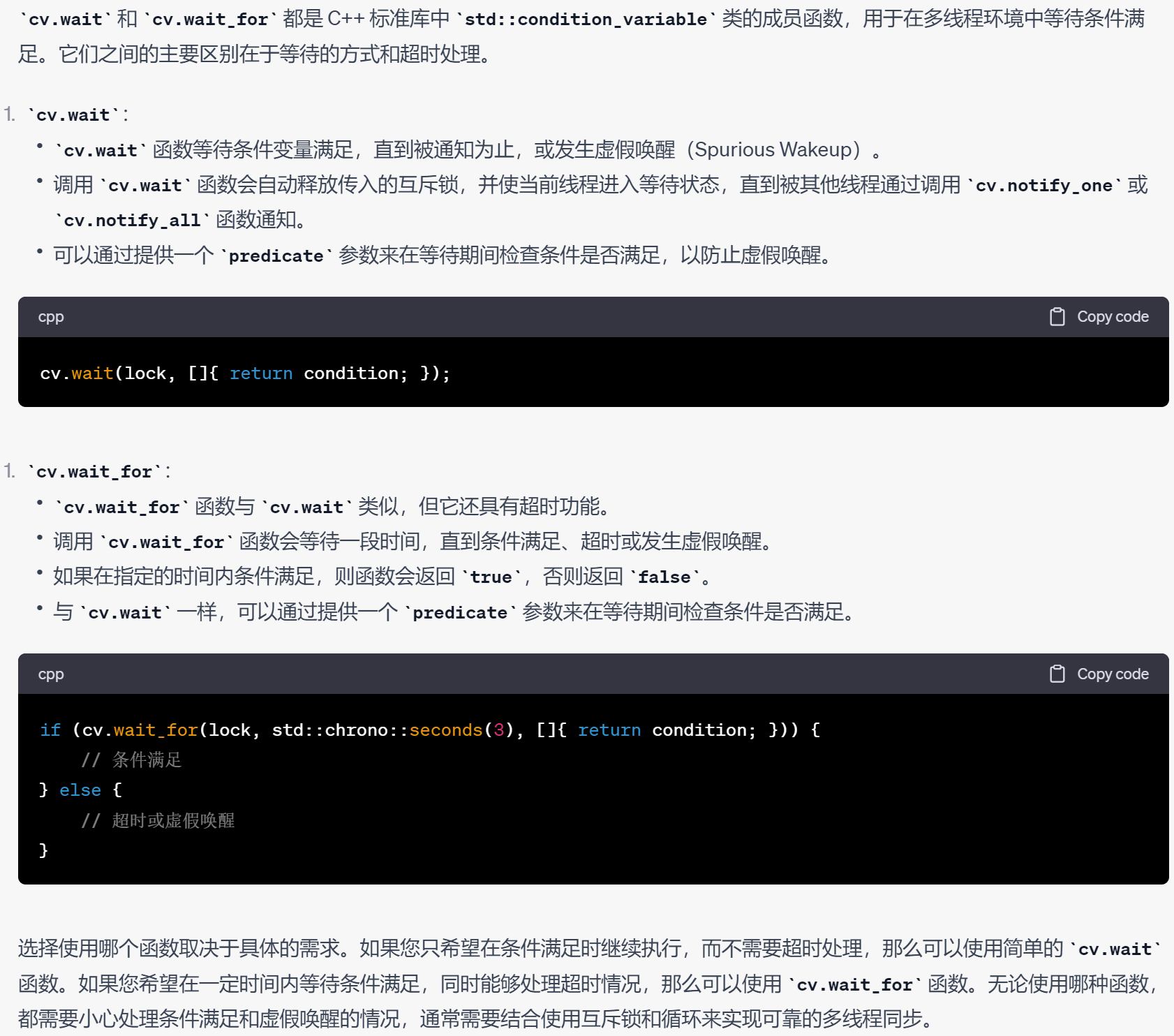
C++笔记之条件变量(Condition Variable)与cv.wait 和 cv.wait_for的使用
C笔记之条件变量(Condition Variable)与cv.wait 和 cv.wait_for的使用 参考博客:C笔记之各种sleep方法总结 code review! 文章目录 C笔记之条件变量(Condition Variable)与cv.wait 和 cv.wait_for的使用1.条件变量&…...

Dubbo之DubboBootstrap源码解析
功能描述 DubboBootstrap是Dubbo的启动类,包含服务启动、初始化、预处理配置、销毁清理等核心功能 功能分析 核心DubboBootstrap类分析 主要成员变量分析 private static volatile DubboBootstrap instance; //缓存者启动类的实例对象,以static形式…...
SpringBoot + Vue 微人事 项目 (第八天)
基础信息设置 在该页面添加一个大div,然后添加一个tab选项卡,Element UI里面有 把代码复制到大div里面,把里面的label和name属性改成我们想要的,再把tab-click"handleClick"去掉 <div><el-tabs v-model"a…...
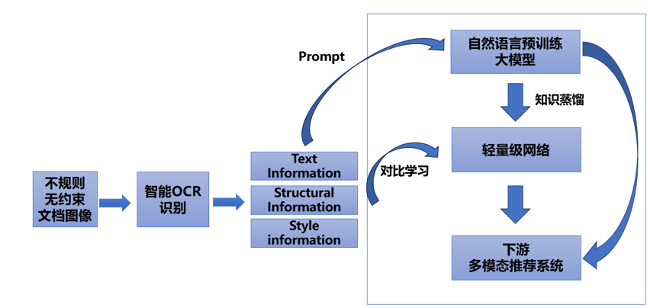
人工智能引领图文扫描新趋势
1. 背景和影响 近日,中国大学生服务外包创新创业大赛决赛在江南大学圆满落幕。为满足现代服务产业企业的现实需求,本次竞赛内容设计充分聚焦企业发展中所面临的技术、管理等现实问题,与产业的结合度更紧密,智能文字识别技术是大赛…...

ChatGPT在智能城市规划和交通优化中的应用如何?
智能城市规划和交通优化是应对城市化挑战、提高城市可持续性的重要领域。在这方面,ChatGPT作为一种强大的自然语言处理模型,可以发挥重要作用,帮助实现更智能、高效的城市规划和交通管理。本文将详细探讨ChatGPT在智能城市规划和交通优化中的…...

探索Perfetto:开源性能追踪工具的未来之光
探索Perfetto:开源性能追踪工具的未来之光 1. 引言 A. 介绍Perfetto的背景和作用 随着移动应用、桌面软件和嵌入式系统的不断发展,软件性能优化变得愈发重要。在这个背景下,Perfetto作为一款开源性能追踪工具,日益引起了开发者…...

A*算法图文详解
基本概念 A*算法最早于1964年在IEEE Transactions on Systems Science and Cybernetics中的论文《A Formal Basis for the Heuristic Determination of Minimum Cost Paths》中首次提出。其属于一种经典的启发式搜索方法,所谓启发式搜索,就在于当前搜索…...

[MySQL] — 数据类型和表的约束
目录 数据类型 数据类型分类 数值类型 tinyint类型 bit类型 小数类型 float decimal 字符串类型 char varchar char和varchar的区别 日期和时间类型 enum 和 set 表的约束 空属性 默认值 列描述 zeorfill 主键 创建表时在字段上指定主键 删除主键: 追…...

JetBrains IDE远程开发功能可供GitHub用户使用
JetBrains与GitHub去年已达成合作,提供GitHub Codespaces 与 JetBrains Gateway 之间的集成。 GitHub Codespaces允许用户创建安全、可配置、专属的云端开发环境,此集成意味着您可以通过JetBrains Gateway使用在 GitHub Codespaces 中运行喜欢的IDE进行…...
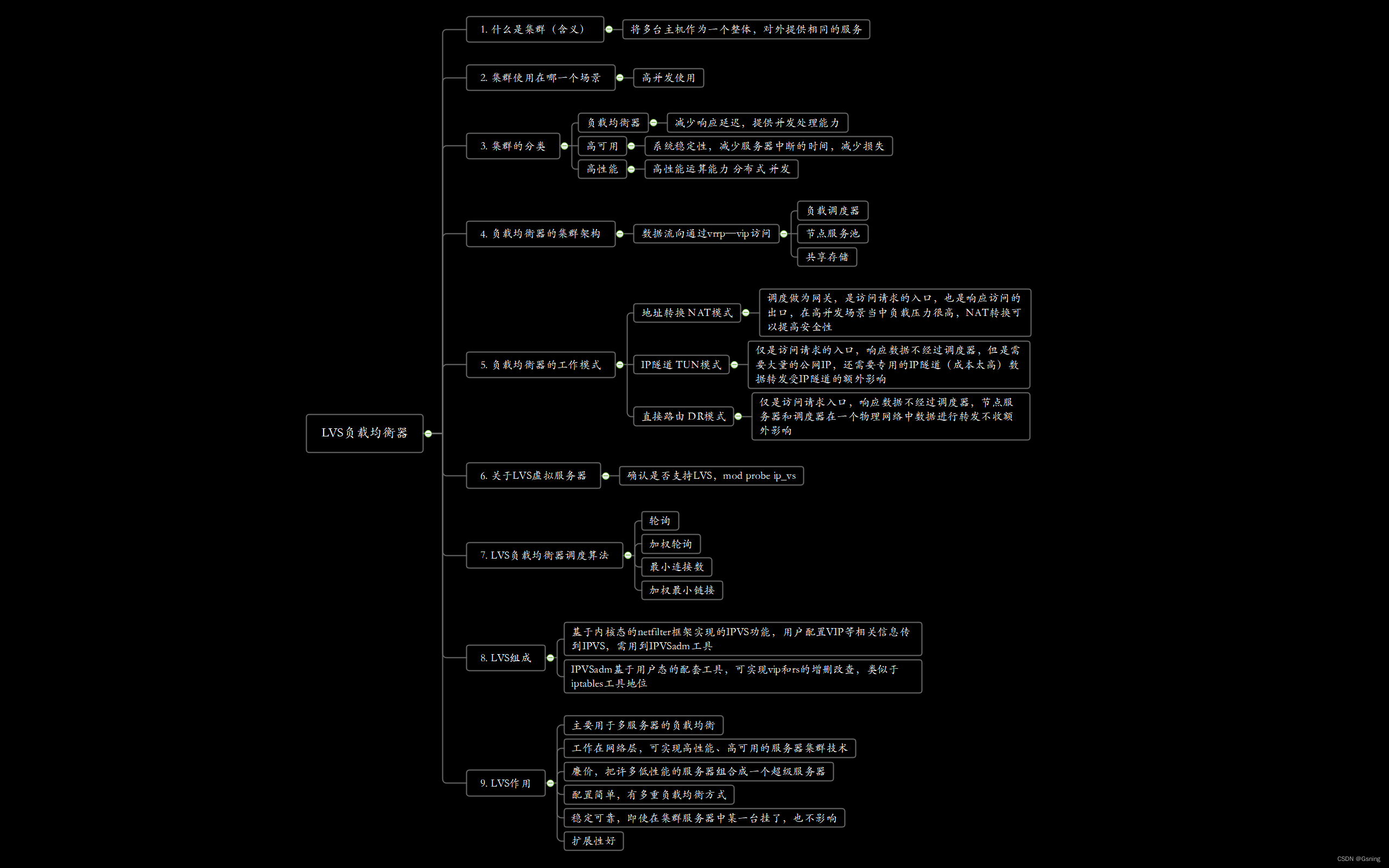
LVS 负载均衡集群
集群 集群(Cluster)是一组相互连接的计算机或服务器,它们通过网络一起工作以完成共同的任务或提供服务。集群的目标是通过将多台计算机协同工作,提高计算能力、可用性、性能和可伸缩性,适用于大量高并发的场景。 集群…...

Mongodb Ubuntu安装
Mongodb Ubuntu安装 1.更新软件源导入MongoDB的GPG密钥 sudo apt update sudo apt install -y dirmngr wget gnupg apt-transport-https ca-certificates software-properties-common gnupgwget -qO - https://www.mongodb.org/static/pgp/server-6.0.asc | sudo apt-key add…...
【Spring Boot 源码学习】自动装配流程源码解析(下)
自动装配流程源码解析(下) 引言往期内容主要内容4. 排除指定自动配置组件5. 过滤自动配置组件6. 触发自动配置事件 总结 引言 上篇博文,笔者带大家了解了自动装配流程中有关自动配置加载的流程; 本篇将介绍自动装配流程剩余的内…...

基于微信小程序的毕业设计题目200例
个人简介:7 年大厂程序员经历,擅长Java、微信小程序、Python、Android等,大家有这一块的问题可以一起交流! 各类成品 java毕设 。javaweb,ssh,ssm,springboot等等项目框架,源码丰富&…...

【数据管理】什么是数据管理?
文章目录 前言常见内容主题领域数据类型元数据引用数据主数据交易数据 数据类型的特点数据类型之间的关系GIGO数据质量评估 数据质量管理数据治理数据安全 前言 数据管理,即对数据资源的管理。按照 DAMA (国际数据管理协会)的定义࿱…...
[oneAPI] 手写数字识别-LSTM
[oneAPI] 手写数字识别-LSTM 手写数字识别参数与包加载数据模型训练过程结果 oneAPI 比赛:https://marketing.csdn.net/p/f3e44fbfe46c465f4d9d6c23e38e0517 Intel DevCloud for oneAPI:https://devcloud.intel.com/oneapi/get_started/aiAnalyticsToolk…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
