Codeforces Round 893 (Div. 2) D.Trees and Segments
原题链接:Problem - D - Codeforces
题面:

大概意思就是让你在翻转01串不超过k次的情况下,使得a*(0的最大连续长度)+(1的最大连续长度)最大(1<=a<=n)。输出n个数,第i个数代表a=i时的最大值。
思路:可以发现n<=3000,我们可以用O(n^2)的复杂度来求解。首先我们先假设最长连续0串在左边,最长的连续1串在右边,一开始最朴素的思想就是:
枚举最长0串的左端点l和右端点r,并且使它合法。设区间[l,r]中1的个数为x,也就是说[l,r]变成全0串需要的操作数为x。然后O(n^2)求出区间[r+1,n]我们能得到的最长1串,长度为y(此时我们能进行的最大操作数为k-x)。我们定义mp[i]:0串长度为i时,1串的最长长度为mp[i]。然后我们更新mp[x]为max(mp[r-l+1],y)即可。
因为这是0串在左,1串在右,所以我们还需要将字符串翻转然后再这样处理一次。
最后输出的时候,每次我们只需要遍历mp,a*i+mp[i]取max即可。
当然这样子操作的总复杂度是O(n^4),我们肯定是不能接受的,那么怎么能让它复杂度降下来呢?我们可以利用dp来预处理,用dp[i][j]来表示[i~n]区间,操作数最大为j时,1串的最大长度。
具体实现见代码注释。
int n,k;
int mp[maxn];
//表示连续0的长度为i的时候,最长连续1的长度最大为mp[i]
string x;
void f() {vector<vector<int>>dp(n+2,vector<int>(k+2));//dp[i][j]表示[i~n]区间,操作数最大为j时,连续1的最大长度。 vector<int>sum(n+2);//sum[i]表示[1,i]中字符1的个数 string s=" "+x;//下标从1开始,防止数组越界 for(int i=n; i>=1; i--) {//预处理出i~n的字符串在操作数为k时候变为1的最大连续串长度dp[i]=dp[i+1]; //大区间可以由小区间的方案转移过来 ,因为在相同操作数下,[i,n]的最长连续1串 >=[i+1,n]的最长连续1串 int cost=0;for(int j=i; j<=n; j++) {cost+=(s[j]=='0');if(cost<=k) dp[i][cost]=max(dp[i][cost],j-i+1);//如果合法,则答案取max else break;//后面的cost都大于k了,直接break }for(int j=1; j<=k; j++) dp[i][j]=max(dp[i][j],dp[i][j-1]);//大的操作数方案可以由小的操作数方案转移过来,因为你用x次操作能办到的,用x+1次操作也一定能办到 }mp[0]=max(mp[0],dp[1][k]);//将全是1,没有0的情况特殊处理 for(int i=1; i<=n; i++)sum[i]=sum[i-1]+(s[i]=='1');//预处理前缀1的个数 for(int i=1; i<=n; i++) {for(int j=i; j<=n; j++) {if(sum[j]-sum[i-1]>k)continue;//如果操作数大于k了则不合法,continue mp[j-i+1]=max(mp[j-i+1],dp[j+1][k-sum[j]+sum[i-1]]);//j-i+1为连续0的长度,k-sum[j]+sum[i-1]为剩下的操作数 }}
}
void solve() {cin>>n>>k>>x;for(int i=0; i<=n; i++) mp[i]=-1;//初始化为-1 f();//处理0串在左,1串在右的情况 reverse(x.begin(),x.end()),f();//等于处理1串在左,0串在右的情况 for(int i=1; i<=n; i++) {int ans=0;for(int j=0; j<=n; j++) {//当0的长度为j时 if(mp[j]!=-1)ans=max(ans,i*j+mp[j]);}cout<<ans<<" ";}cout<<endl;
}
相关文章:

Codeforces Round 893 (Div. 2) D.Trees and Segments
原题链接:Problem - D - Codeforces 题面: 大概意思就是让你在翻转01串不超过k次的情况下,使得a*(0的最大连续长度)(1的最大连续长度)最大(1<a<n)。输出n个数&…...
SpringBoot + Vue 前后端分离项目 微人事(九)
职位管理后端接口设计 在controller包里面新建system包,再在system包里面新建basic包,再在basic包里面创建PositionController类,在定义PositionController类的接口的时候,一定要与数据库的menu中的url地址到一致,不然…...

【业务功能篇71】Cglib的BeanCopier进行Bean对象拷贝
选择Cglib的BeanCopier进行Bean拷贝的理由是, 其性能要比Spring的BeanUtils,Apache的BeanUtils和PropertyUtils要好很多, 尤其是数据量比较大的情况下。 BeanCopier的主要作用是将数据库层面的Entity转化成service层的POJO。BeanCopier其实已…...
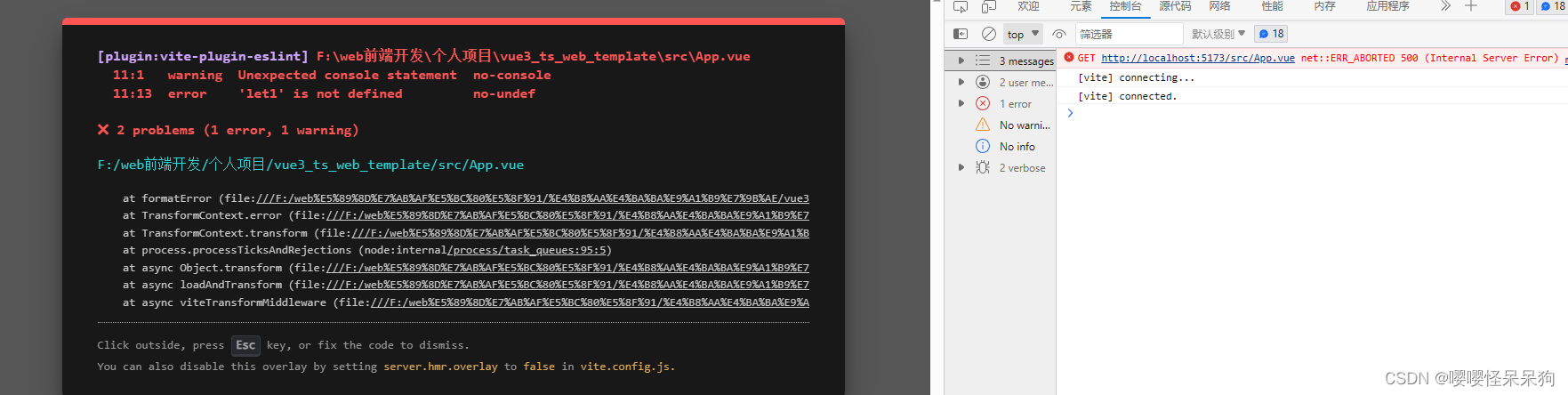
让eslint的错误信息显示在项目界面上
1.需求描述 效果如下 让eslint中的错误,显示在项目界面上 2.问题解决 1.安装 vite-plugin-eslint 插件 npm install vite-plugin-eslint --save-dev2.配置插件 // vite.config.js import { defineConfig } from vite import vue from vitejs/plugin-vue import e…...
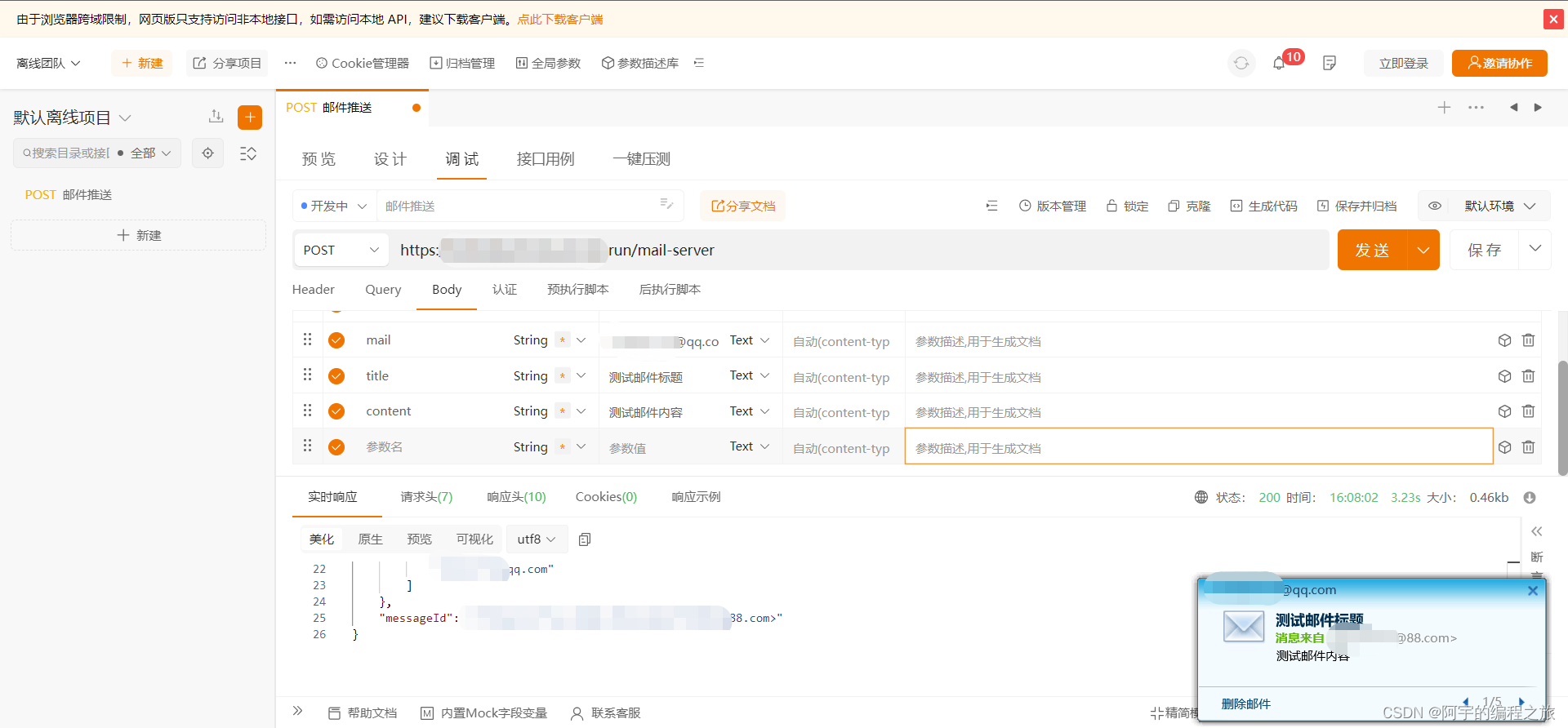
手摸手带你实现一个开箱即用的Node邮件推送服务
目录 编辑 前言 准备工作 邮箱配置 代码实现 服务部署 使用效果 题外话 写在最后 相关代码: 前言 由于邮箱账号和手机号的唯一性,通常实现验证码的校验时比较常用的两种方式是手机短信推送和邮箱推送,此外,邮件推送服…...

【Linux网络】网络编程套接字 -- 基于socket实现一个简单UDP网络程序
认识端口号网络字节序处理字节序函数 htonl、htons、ntohl、ntohs socketsocket编程接口sockaddr结构结尾实现UDP程序的socket接口使用解析socket处理 IP 地址的函数初始化sockaddr_inbindrecvfromsendto 实现一个简单的UDP网络程序封装服务器相关代码封装客户端相关代码实验结…...
)
Python学习笔记第六十四天(Matplotlib 网格线)
Python学习笔记第六十四天 Matplotlib 网格线普通网格线样式网格线 后记 Matplotlib 网格线 我们可以使用 pyplot 中的 grid() 方法来设置图表中的网格线。 grid() 方法语法格式如下: matplotlib.pyplot.grid(bNone, whichmajor, axisboth, )参数说明:…...
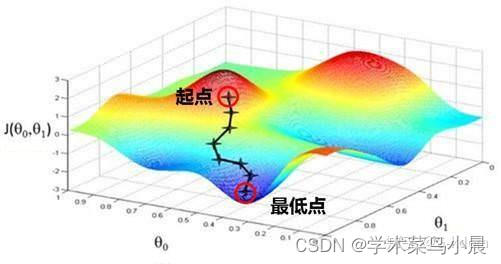
机器学习与模式识别3(线性回归与逻辑回归)
一、线性回归与逻辑回归简介 线性回归主要功能是拟合数据,常用平方误差函数。 逻辑回归主要功能是区分数据,找到决策边界,常用交叉熵。 二、线性回归与逻辑回归的实现 1.线性回归 利用回归方程对一个或多个特征值和目标值之间的关系进行建模…...
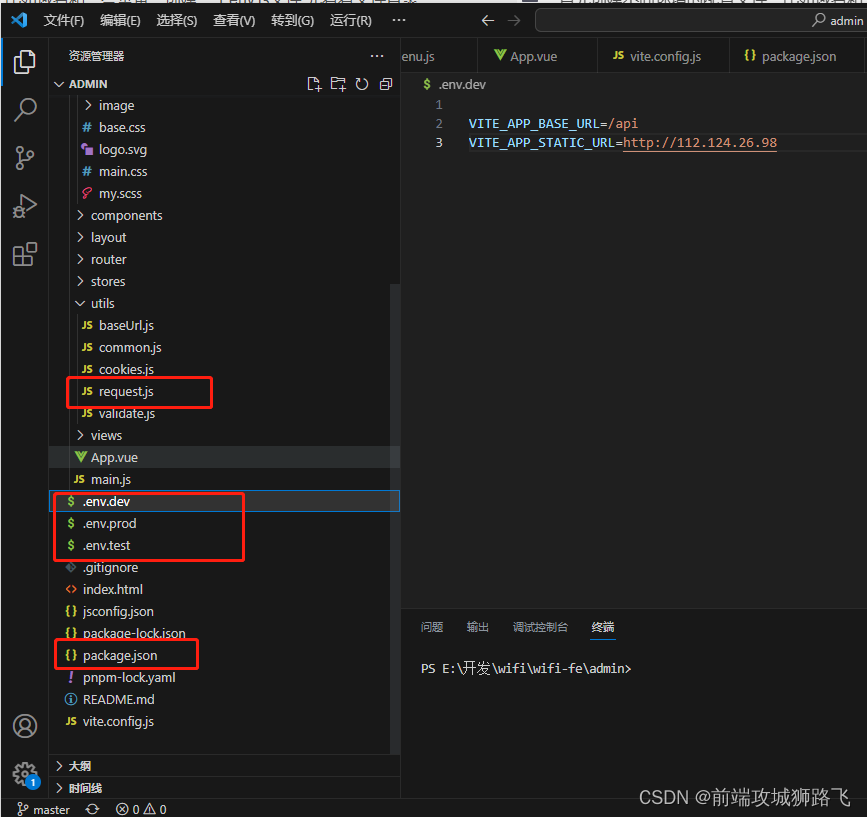
vue启动配置npm run serve,动态环境变量,根据不同环境访问不同域名
首先创建不同环境的配置文件,比如域名和一些常量,创建一个env文件,先看看文件目录 env.dev就是dev环境的域名,.test就是test环境域名,其他同理,然后配置package.json文件 {"name": "require-admin&qu…...

HTML <strike> 标签
HTML5 中不支持 <strike> 标签在 HTML 4 中用于定义删除线文本。 定义和用法 <strike> 标签可定义加删除线文本定义。 浏览器支持 元素ChromeIEFirefoxSafariOpera<strike>YesYesYesYesYes 所有浏览器都支持 <strike> 标签。 HTML 与 XHTML 之间…...
)
数学建模-模型详解(1)
规划模型 线性规划模型: 当涉及到线性规划模型实例时,以下是一个简单的示例: 假设我们有两个变量 x 和 y,并且我们希望最大化目标函数 Z 5x 3y,同时满足以下约束条件: x > 0y > 02x y < 10…...

MySQL 数据库表的基本操作
一、数据库表概述 在数据库中,数据表是数据库中最重要、最基本的操作对象,是数据存储的基本单位。数据表被定义为列的集合,数据在表中是按照行和列的格式来存储的。每一行代表一条唯一的记录,每一列代表记录中的一个域。 二、数…...
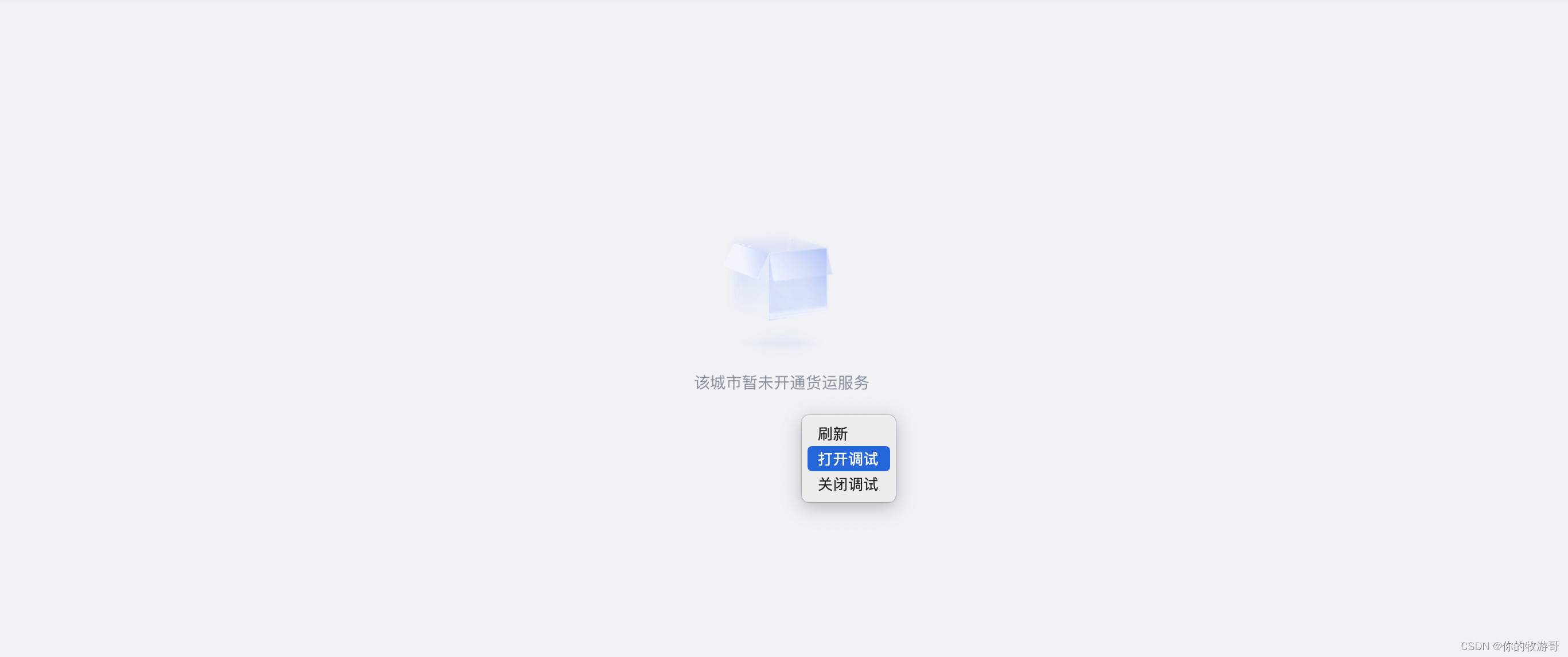
企业微信电脑端开启chrome调试
首先: Mac端调试开启的快捷键:control shift command d Window端调试开启的快捷键: control shift alt d 这边以Mac为例,我们可以在电脑顶部看到调试的入口: 然后我们点击 『浏览器、webView相关』菜单,勾选上…...
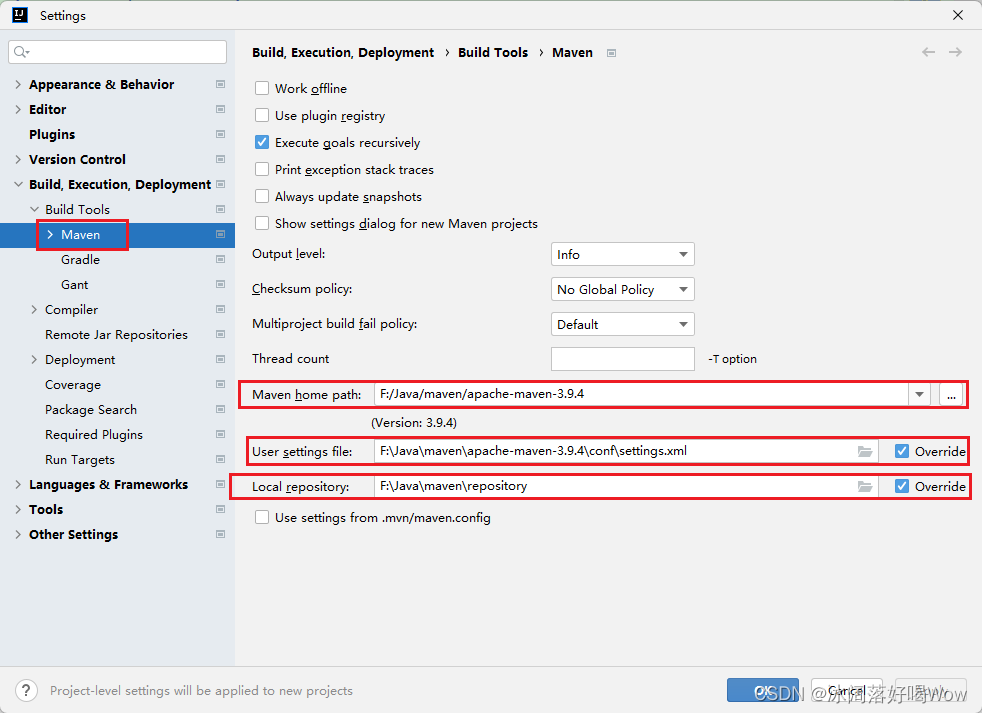
Maven官网下载配置新仓库
1.Maven的下载 Maven的官网地址:Maven – Download Apache Maven 点击Download,查找 Files下的版本并下载如下图: 2.Maven的配置 自己在D盘或者E盘创建一个文件夹,作为本地仓库,存放项目依赖。 将下载好的zip文件进行解…...

银河麒麟V10 达梦安装教程
安装前先准备要安装包,包需要需要区分X86和arm架构。 版本为:dm8_20230419_FTarm_kylin10_sp1_64.iso 达梦数据库下载地址: https://www.aliyundrive.com/s/Qm7Es5BQM5U 第一步创建用户 su - root 1. 创建安装用户组 dminstall。 groupad…...
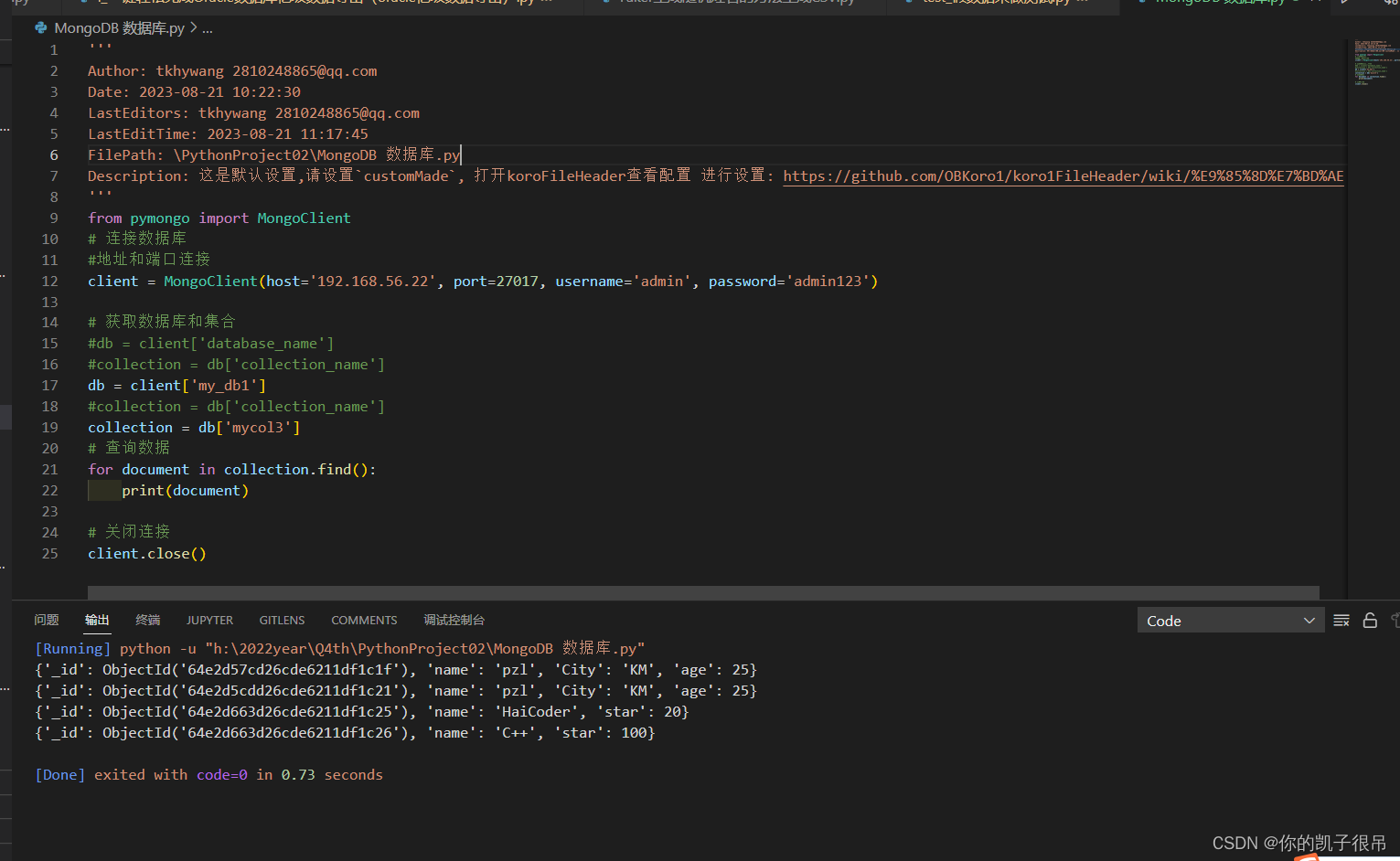
Python操作MongoDB数据库
安装MongoDB库 pip install pymongopython 代码 Author: tkhywang 2810248865qq.com Date: 2023-08-21 10:22:30 LastEditors: tkhywang 2810248865qq.com LastEditTime: 2023-08-21 11:17:45 FilePath: \PythonProject02\MongoDB 数据库.py Description: 这是默认设置,请设置…...
《HeadFirst设计模式(第二版)》第十一章代码——代理模式
代码文件目录: RMI: MyRemote package Chapter11_ProxyPattern.RMI;import java.rmi.Remote; import java.rmi.RemoteException;public interface MyRemote extends Remote {public String sayHello() throws RemoteException; }MyRemoteClient packa…...
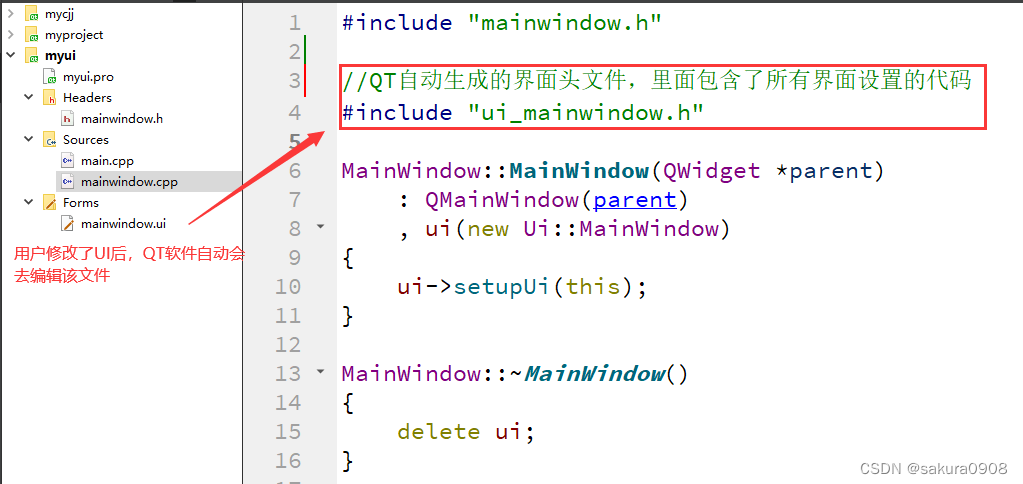
QT的工程文件认识
目录 1、QT介绍 2、QT的特点 3、QT模块 3.1基本模块 3.2扩展模块 4、QT工程创建 1.选择应用的窗体格式 2.设置工程的名称与路径 3.设置类名 4.选择编译器 5、QT 工程解析 xxx.pro 工程配置 xxx.h 头文件 main.cpp 主函数 xxx.cpp 文件 6、纯手工创建一个QT 工程…...
typeScript安装及TypeScript tsc 不是内部或外部命令,也不是可运行的程序或批处理文件解决办法
一、typeScript安装: 1、首先确定系统中已安装node, winr 输入cmd 打开命令行,得到版本号证明系统中已经安装node node -v //v18.17.0 2、使用npm 全局安装typeScript # 全局安装 TypeScript npm i -g typescript 二、检查是否安装成功ts #检查t…...

SWUST 派森练习题:P111. 摩斯密码翻译器
描述 摩斯密码(morse code),又称摩斯电码、摩尔斯电码(莫尔斯电码),是一种时通时断的信号代码,通过不同的信号排列顺序来表达不同的英文字母、数字和标点符号;通信时,将英文字母等内…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
