论文导读|European Journal of Operational Research近期文章精选:旅行商问题专题

推文作者:王松阁
编者按
在“European Journal of Operational Research近期论文精选”中,我们有主题、有针对性地选择了European Journal of Operational Research中一些有趣的文章,不仅对文章的内容进行了概括与点评,而且也对文章的结构进行了梳理,旨在激发广大读者的阅读兴趣与探索热情。在本期“论文精选”中,我们以“旅行商问题”为主题,分别探究了先行约束广义旅行商问题、广义近似旅行商问题、非对称旅行商问题,涉及整数规划、分支切割、锥规划、迭代贪心等诸多知识。
推荐文章1
● 题目:Precedence constrained generalized traveling salesman problem: Polyhedral study, formulations, and branch-and-cut algorithm
先行约束广义旅行商问题:多面体研究、公式化和分支切割算法
● 期刊:European Journal of Operational Research
● 原文链接:https://doi.org/10.1016/j.ejor.2023.01.039
● 作者:Daniil Khachai, Ruslan Sadykov, Olga Battaiaa, Michael Khachay
● 关键词:
Travelling salesman(旅行商问题),Integer programming(整数规划),Branch-and-cut algorithm(分支切割算法),Facet-inducing inequalities(面诱导不等式),Polyhedral structure(多面体结构)
● 摘要:
The Precedence Constrained Generalized Traveling Salesman Problem (PCGTSP) is an extension of two well-known combinatorial optimization problems - the Generalized Traveling Salesman Problem (GTSP) and the Precedence Constrained Asymmetric Traveling Salesman Problem (PCATSP), whose path version is known as the Sequential Ordering Problem (SOP). Similarly to the classic GTSP, the goal of the PCGTSP, for a given input digraph and partition of its node set into clusters, is to find a minimum cost cyclic route (tour) visiting each cluster in a single node. In addition, as in the PCATSP, feasible tours are restricted to visit the clusters with respect to the given partial order. Unlike the GTSP and SOP, to the best of our knowledge, the PCGTSP still remain to be weakly studied both in terms of polyhedral theory and algo-rithms. In this paper, for the first time for the PCGTSP, we propose several families of valid inequalities, establish dimension of the PCGTS polytope and prove sufficient conditions ensuring that the extended Balas' pi- and sigma-inequalities become facet-inducing. Relying on these theoretical results and evolving the state-of-the-art algorithmic approaches for the PCATSP and SOP, we introduce a family of MILP-models (formulations) and several variants of the branch-and-cut algorithm for the PCGTSP. We prove their high performance in a competitive numerical evaluation against the public benchmark library PCGTSPLIB, a known adaptation of the classic SOPLIB to the problem in question.
先行约束广义旅行商问题(PCGTSP)是两个著名的组合优化问题的扩展,分别是广义旅行商问题(GTSP)和先行约束不对称旅行商问题(PCATSP),其路径版本被称为顺序排列问题(SOP)。与经典GTSP类似,对于给定的输入有向图和将其节点集划分为簇的方式,PCGTSP的目标是找到一个最小成本的环路(路径),使得每个簇都在一个节点中被访问。此外,与PCATSP类似,可行的路径被限制为按照给定的偏序访问簇。与GTSP和SOP不同的是,就我们所知,PCGTSP在多面体理论和算法方面仍然缺乏深入研究。在本文中,我们首次针对PCGTSP提出了几类有效的不等式,建立了PCGTSP多面体的维度,并证明了确保扩展的Balas' π - 和 σ -不等式成为面诱导的充分条件。基于这些理论结果,并借鉴了PCATSP和SOP的最先进算法方法,我们提出了一系列线性整数规划(MILP)模型和PCGTSP的分支定界算法的多个变体。我们证明了它们在公共基准库PCGTSPLIB上进行的竞争性数值评估中表现出很高的性能,该基准库是将经典SOPLIB改编成与问题相应的版本。
● 文章结构:
● 点评:
本文对先行约束广义旅行商问题 (PCGTSP)进行了系统研究,涵盖了多面体研究和算法分析两个方面。文章扩展了已有的PCATSP结果,提出了多种新颖的有效不等式,并对PCGTS多面体的维度进行了分析。也首次为PCGTSP问题提出了一种分支切割算法,为解决该问题提供了新的算法思路。
推荐文章2
● 题目:The generalized close enough traveling salesman problem
广义近似旅行商问题
● 期刊:European Journal of Operational Research
● 原文链接:https://doi.org/10.1016/j.ejor.2023.04.010
● 作者:Andrea Di Placido, Claudia Archetti, Carmine Cerrone, Bruce Goldend
● 关键词:
Metaheuristics(元启发式算法),Close enough traveling salesman problem(广义近似旅行商问题),Genetic algorithms(遗传算法),Conic programming(锥规划)
● 摘要:
This paper studies a generalization of the close enough traveling salesman problem referred to as the generalized close enough traveling salesman problem (GCETSP). The canonical problem contains a set of customers, each associated with an area (neighborhood) that is generally circular. In the GCETSP, each customer is associated with a set of disks with different radii. Having multiple disks around the customer allows us to model several real-world applications, in which a higher benefit is gained by more closely approaching each target. A prize is assigned to each disk and is collected if the disk is traversed. The goal is to determine the route that visits each customer and the depot and maximizes the difference between the total collected prize and the route length. The total collected prize is given by the sum of the customer prices' associated with the innermost disk traversed by the route. We propose a heuristic algorithm and an evolutionary approach, specifically, a genetic algorithm (GA), to solve this problem. We evaluate the GA's performance on instances generated from benchmark CETSP and TSP instances. We then compare GA solutions with CETSP solutions and solutions obtained through an alternative approach based on pre-selecting intersection points with customers' disks. The results show that the GA can identify high-quality solutions with a short computing time.
本文研究了近似旅行商问题的一种推广,称为广义近似旅行商问题(GCETSP)。经典问题包含一组客户,每个客户与一个圆形的区域相关联。在GCETSP中,每个客户与一组具有不同半径的圆盘相关联。围绕一位客户有多个不同圆盘来模拟现实世界的几种不同应用,更接近目标的圆盘会获得更高效益。每个圆盘具有对应的奖励值,穿越该圆盘时即可获得相应奖励。目标是确定访问每个客户和中转站的路线,最大化总收集奖励和路线长度的差值,总收集奖励为路线穿越的最内圆盘所对应的客户价格之和。我们提出了一种启发式算法和一种遗传算法(GA)来解决这个问题,并利用CETSP和TSP的基准算例所生成的实例来评估遗传算法的性能。然后将GA的解与CETSP解以及通过基于预先选择与客户圆盘的交点的替代方法所得到的解进行比较,结果显示GA能够在短时间内识别出高质量的解。
● 文章结构:
● 点评:
本文采用遗传算法(GA)和构造算法来解决GCETSP问题。GA针对GCETSP的特殊特点进行了优化,构造算法则基于解决TSP、SOCP和最短路径问题的顺序来构建可行路径。这两种方法为解决GCETSP提供了有效的工具。通过与另一种启发式方法nearOpt进行对比实验,GA表现出更好的性能。本研究在无人机使用中的抄表、RFID系统等现实应用的建模优化中具有一定启示。
推荐文章3
● 题目:An asymmetric traveling salesman problem based matheuristic algorithm for flowshop group scheduling problem
一种基于非对称旅行商问题的数学启发式算法,用于流水车间群调度问题
● 期刊:European Journal of Operational Research
● 原文链接:https://doi.org/10.1016/j.ejor.2023.03.038
● 作者:Xuan He, Quan-Ke Pan, Liang Gao, Janis S. Neufeld
● 关键词:
Scheduling(调度),Asymmetric traveling salesman(非对称旅行商),Branch-and-cut(分枝切割法),Iterated greedy(迭代贪心),Matheuristic(数学启发式)
● 摘要:
The flowshop group scheduling problem (FGSP) has become a hot research problem owing to its practical applications in modern industry in recent years. The FGSP can be regarded as a combination of two cou-pled sub-problems. One is the group scheduling sub-problem with sequence-dependent setup times. The other is the job scheduling sub-problem within each group. A mixed integer linear programming model is built for the FGSP with the makespan criterion. Based on the problem-specific knowledge, i.e., the sequence-dependent group setup times are greater than the processing time of jobs, and the number of machines is small, the group scheduling sub-problem is approximated into an asymmetric traveling sales-man problem (ATSP). Then, a matheuristic algorithm (MA) is proposed by integrating a branch-and-cut algorithm and an iterated greedy (IG) algorithm, where the branch-and-cut algorithm is used to generate the optimal Hamiltonian circuit for sub-group sequences of a group sequence obtained by the IG. On 405 test instances, the proposed MA performs significantly better than several state-of-the-art algorithms in the literature.
近年来,由于在现代工业中的实际应用,流水车间群调度问题(FGSP)已成为一个热门的研究问题。FGSP可以看作是两个耦合子问题的组合。一个是带有序列相关设置时间的群调度子问题,另一个是每个群内的作业调度子问题。针对以最大完工时间为目标的FGSP,建立了一个混合整数线性规划模型。基于问题特定的知识,即序列相关的群设置时间大于作业的处理时间,并且机器数量较少,将群调度子问题近似为不对称旅行商问题(ATSP)。然后,提出了一种数学启发式算法(MA),它将分支定界算法和迭代贪心(IG)算法结合在一起,其中分支定界算法用于为由IG得到的群序列的子群序列生成最优哈密顿回路。在405个测试实例上,所提出的MA表现明显优于文献中几种最先进的算法。
● 文章结构:
● 点评:
本研究主要针对流水车间分组调度问题(FCSP)的最大完工时间准则展开研究,提出了一种新颖的数学启发式算法(MA)。研究创新点包括在问题层面上将分组调度子问题近似为非对称旅行商问题(ATSP),并在算法层面上采用分支定界和迭代贪心算法的结合。还针对问题特点设计了特殊的局部搜索和断续规则机制,以增强迭代贪心算法的搜索性能。该算法在解决能够近似为非对称旅行商问题的流水车间调度问题上表现出色,对于一些经典的流水车间调度问题,如无等待流水车间调度问题和阻塞流水车间调度问题,该算法同样适用。
相关文章:

论文导读|European Journal of Operational Research近期文章精选:旅行商问题专题
推文作者:王松阁 编者按 在“European Journal of Operational Research近期论文精选”中,我们有主题、有针对性地选择了European Journal of Operational Research中一些有趣的文章,不仅对文章的内容进行了概括与点评,而且也对文…...

playwright迭代元素
DOM结构 <ul><li>apple</li><li>banana</li><li>orange</li> </ul>迭代元素操作 通过 page.get_by_role("listitem") 会匹配到 apple, banana, orange, 如果要对这一组数据中的每个元素进行操作&#…...

65 | 增长模型案例
增长模型代表了一种综合性的方法论,旨在通过深入了解用户行为、市场趋势和数据洞察,来指导企业制定有效的增长战略。这种方法突破了传统的经验主义,将决策过程建立在数据驱动和实验的基础之上。增长模型不仅仅是一种理论,更是一种实际操作的框架,帮助企业在各个层面实现业…...
Django视图-HttpRequest请求对象和HttpResponse响应对象
文章目录 HttpRequestHttpResponse实践request对象的属性和方法响应 def index(request): 这个request其实就是内部已经封装好的Http请求HttpRequest,它是一个请求对象Django中的视图主要用来接受Web请求,并做出响应。 视图的本质就是一个Python中的函数…...

原来Lambda表达式是这样写的
原来Lambda表达式是这样写的 lambda 是一个匿名函数,我们可以把 lambda 表达式理解为是一段可以传递的代码。 lambda 简明地将代码或方法作为参数传递进去执行。 函数式编程:核心是把函数作为值。 函数式接口 :只有一个抽象方法的接口称之…...

smartsofthelp 5.0 最专业的数据库优化工具,数据库配置优化,数据库高并发优化,SQL 语句优化...
下载地址:百度网盘 请输入提取码 SQL操作返回历史记录: 2023-08-21 20:42:08:220 输入:select version as 版本号 2023-08-21 20:42:08:223 输出:当前数据库实例版本号:Microsoft SQL Server 2012 - 11.0.2100.60 (X64) …...

智影 R100:首款三维Mesh建模的SLAM激光扫描仪
近年来,激光SLAM系统凭借其更加快速且准确获取更丰富信息的优势,迅速风靡测绘领域,让原本耗时耗力的外业测量变得更加高效。手持激光扫描仪作为基于激光SLAM技术衍生的众多产品之一,相较于架站式激光扫描仪更加轻巧便利࿰…...

Next.js - Loading UI and Streaming
特殊文件 loading.js 可帮助您使用 React Suspense 创建有意义的加载用户界面。使用此约定,您可以在加载路由段内容时显示来自服务器的即时加载状态。渲染完成后,新的内容会自动切换进来。 即时加载状态 即时加载状态是在导航时立即显示的后备用户界面…...

快速解决Ubuntu 中 wine 程序 中文显示为方块/显示错误/无法显示中文(2023)
解决办法就是在创建prefix的命令行里加上LANG“zh_CN.UTF8” 或 LC_ALL“zh_CN.UTF8”,并安装cjkfonts,即可。 1、生成prefix、安装cjk字体 以下是基本流程: 现在假定wine和winetricks已经装好, // 先创建一个prefix࿰…...
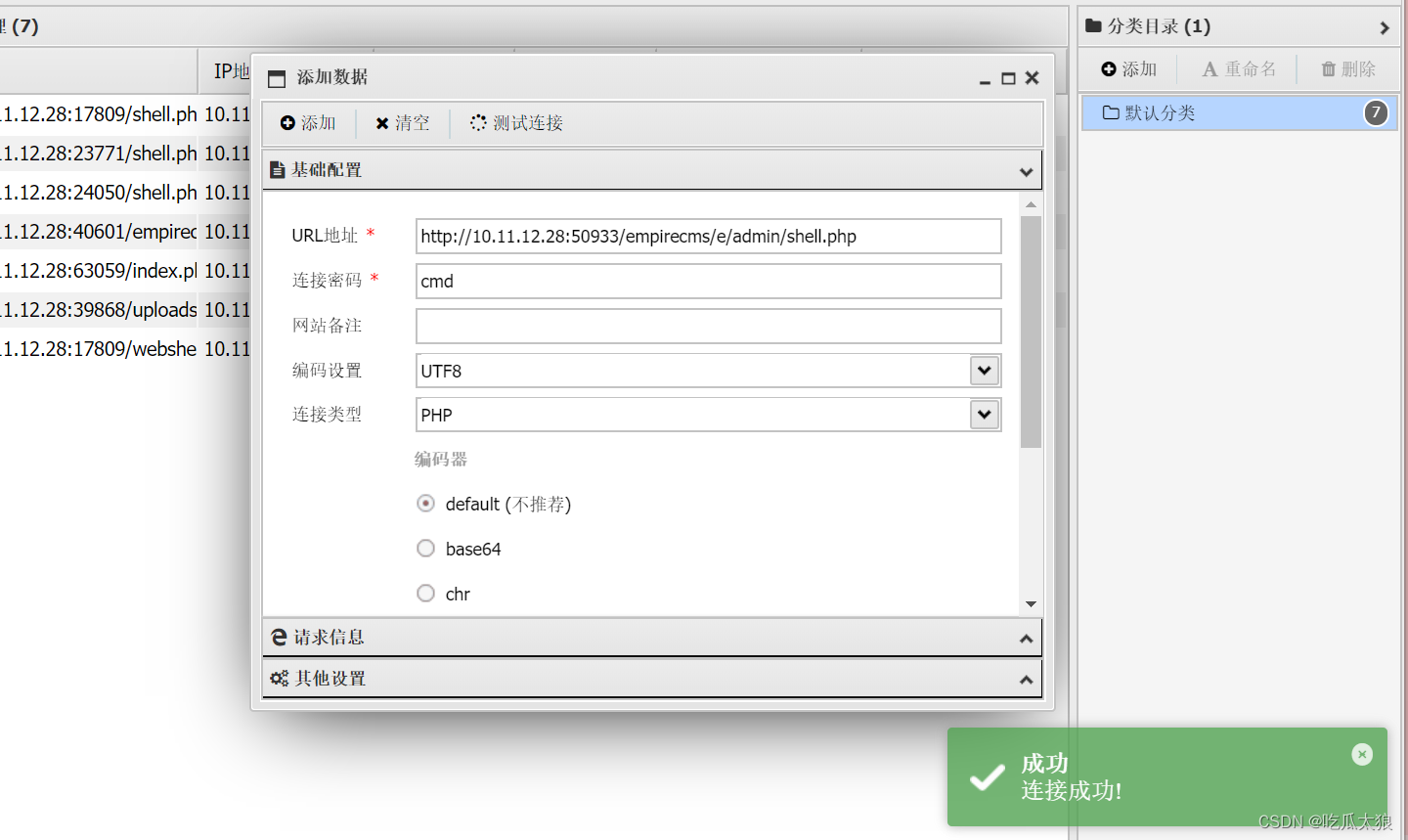
漏洞指北-VulFocus靶场专栏-中级02
漏洞指北-VulFocus靶场专栏-中级02 中级005 🌸thinkphp lang 命令执行(thinkphp:6.0.12)🌸step1:burp suite 抓包 修改请求头step2 修改成功,访问shell.php 中级006 🌸Metabase geojson任意文件…...

【开源三方库】bignumber.js:一个大数数学库
OpenHarmony(OpenAtom OpenHarmony简称“OpenHarmony”)三方库,是经过验证可在OpenHarmony系统上可重复使用的软件组件,可帮助开发者快速开发OpenHarmony应用。如果是发布到开源社区,称为开源三方库,开发者…...

【C++】iota函数 + sort函数实现基于一个数组的多数组对应下标绑定排序
目录 一、iota函数 1. 函数解析 ① 迭代器类型(补充) ② 头文件 ③ 参数 2. 函数用途与实例 二、sort函数 1、 函数解读 2、实现倒序排列 2.1 greater 与 less 模板参数 2.2 lambda表达式 三、下标绑定排序(zip) --- 833.字符串中的查找与替换 一、…...

C# window forms 进度条实现
在 C# Windows Forms 应用程序中,如果在后台执行长时间运行的任务,并希望同时更新进度条,可以使用多线程来实现。这将确保进度条的更新不会阻塞主线程,从而保持界面的响应性。以下是一个示例,演示了如何在后台执行任务…...

ListNode相关
目录 2. 链表相关题目 2.1 合并两个有序链表(简单):递归 2.2 删除排序链表中的重复元素(简单):一次遍历 2.3 两链表相加(中等):递归 2.4 删除链表倒数第N个节点&…...
docker的资源控制及docker数据管理
目录 一.docker的资源控制 1.CPU 资源控制 1.1 资源控制工具 1.2 cgroups有四大功能 1.3 设置CPU使用率上限 1.4 进行CPU压力测试 1.5 设置50%的比例分配CPU使用时间上限 1.6 设置CPU资源占用比(设置多个容器时才有效) 1.6.1 两个容器测试cpu 2&…...
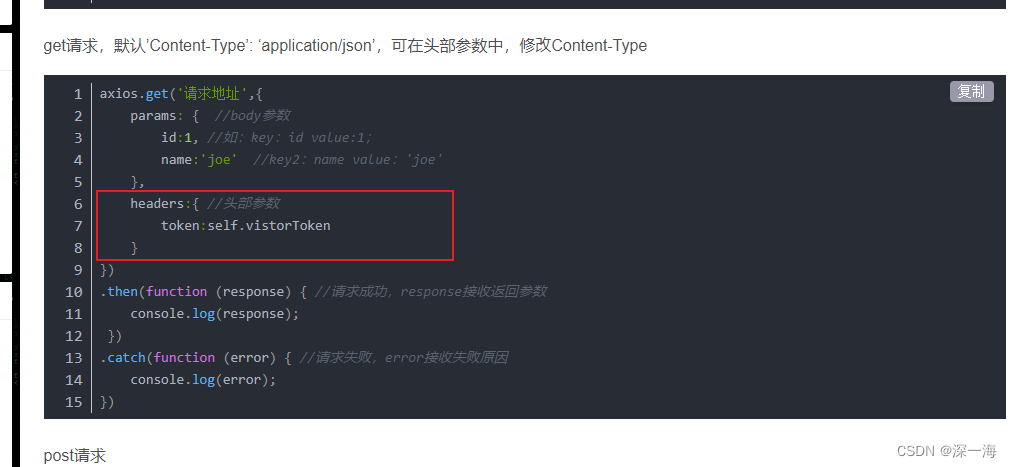
通过请求头传数据向后端发请求
axios (get post请求、头部参数添加)傻瓜式入门axios_axiospost请求参数_web_blog的博客-CSDN博客...
产品流程图是什么?怎么做?
产品流程图是什么? 产品流程图是一种图形化的表达方式,用于描述产品开发、制造、销售、使用等各个阶段中涉及的流程、步骤和关系。它通过图形符号、箭头、文本等元素,展示了产品的各个环节之间的关联和顺序,通常被用于可视化产…...

面试之快速学习STL-map
关联式容器 包括 map、multimap、set 以及 multiset 这 4 种容器。和序列式容器区别: a . 关联式容器在存储元素时还会为每个元素在配备一个键,整体以键值对的方式存储到容器中。 b . 相比前者,关联式容器可以通过键值直接找到对应的元素&am…...
ES的索引结构与算法解析
提到ES,大多数爱好者想到的都是搜索引擎,但是明确一点,ES不等同于搜索引擎。不管是谷歌、百度、必应、搜狗为代表的自然语言处理(NLP)、爬虫、网页处理、大数据处理的全文搜索引擎,还是有明确搜索目的的搜索行为,如各大…...

32.Netty源码之服务端如何处理客户端新建连接
highlight: arduino-light 服务端如何处理客户端新建连接 Netty 服务端完全启动后,就可以对外工作了。接下来 Netty 服务端是如何处理客户端新建连接的呢? 主要分为四步: md Boss NioEventLoop 线程轮询客户端新连接 OP_ACCEPT 事件ÿ…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
