leetcode304. 二维区域和检索 - 矩阵不可变(java)
前缀和数组
- 二维区域和检索 - 矩阵不可变
- 题目描述
- 前缀和
- 代码演示
- 一维数组前缀和
二维区域和检索 - 矩阵不可变
难度 - 中等
原题链接 - 二维区域和检索 - 矩阵不可变
题目描述
给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2) 。
实现 NumMatrix 类:
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。
示例1:
输入:
[“NumMatrix”,“sumRegion”,“sumRegion”,“sumRegion”]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-105 <= matrix[i][j] <= 1e5
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 104 次 sumRegion 方法

前缀和
和一维数组类似.也是先定义一个前缀和数组,求出前缀和的值,然后调用区间值时,就可以用前缀和进行计算.
注意:前缀和数组下标从1开始.
代码演示
class NumMatrix {int[][] sums;public NumMatrix(int[][] matrix) {int m = matrix.length;if (m > 0) {int n = matrix[0].length;sums = new int[m + 1][n + 1];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];}}}}public int sumRegion(int row1, int col1, int row2, int col2) {return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];}}
一维数组前缀和
leetcode303. 区域和检索 - 数组不可变
相关文章:

leetcode304. 二维区域和检索 - 矩阵不可变(java)
前缀和数组 二维区域和检索 - 矩阵不可变题目描述前缀和代码演示 一维数组前缀和 二维区域和检索 - 矩阵不可变 难度 - 中等 原题链接 - 二维区域和检索 - 矩阵不可变 题目描述 给定一个二维矩阵 matrix,以下类型的多个请求: 计算其子矩形范围内元素的总…...
记一次oracle数据库迁移至mysql数据库(表同步)
目录 一、利用Navicat将oracle迁移至mysql数据库 1、建立数据传输 2、选择需要迁移的数据库跟目标库 3、数据传输选项 4、选择需要迁移表信息 二、迁移之后遇到的一些问题 1、大小写问题 2、数据库函数问题 3、sql语句是否使用空格隔开问题 4、关于子查询别命名问题 …...

打怪升级之从零开始的网络协议
序言 三个多月过去了,我又来写博客了,这一次从零开始学习网络协议。 总的来说,计算机网络很像现实生活中的快递网络,其最核心的目标,就是把一个包裹(信息)从A点发送到B点去。下面是一些共同的…...

Lnton羚通算法算力云平台【PyTorch】教程:torch.nn.Softsign
torch.nn.Softsign 原型 CLASS torch.nn.Softsign() 图 代码 import torch import torch.nn as nnm nn.Softsign() input torch.randn(4) output m(input)print("input: ", input) print("output: ", output)# input: tensor([ 0.0046, -0.4135, -2…...
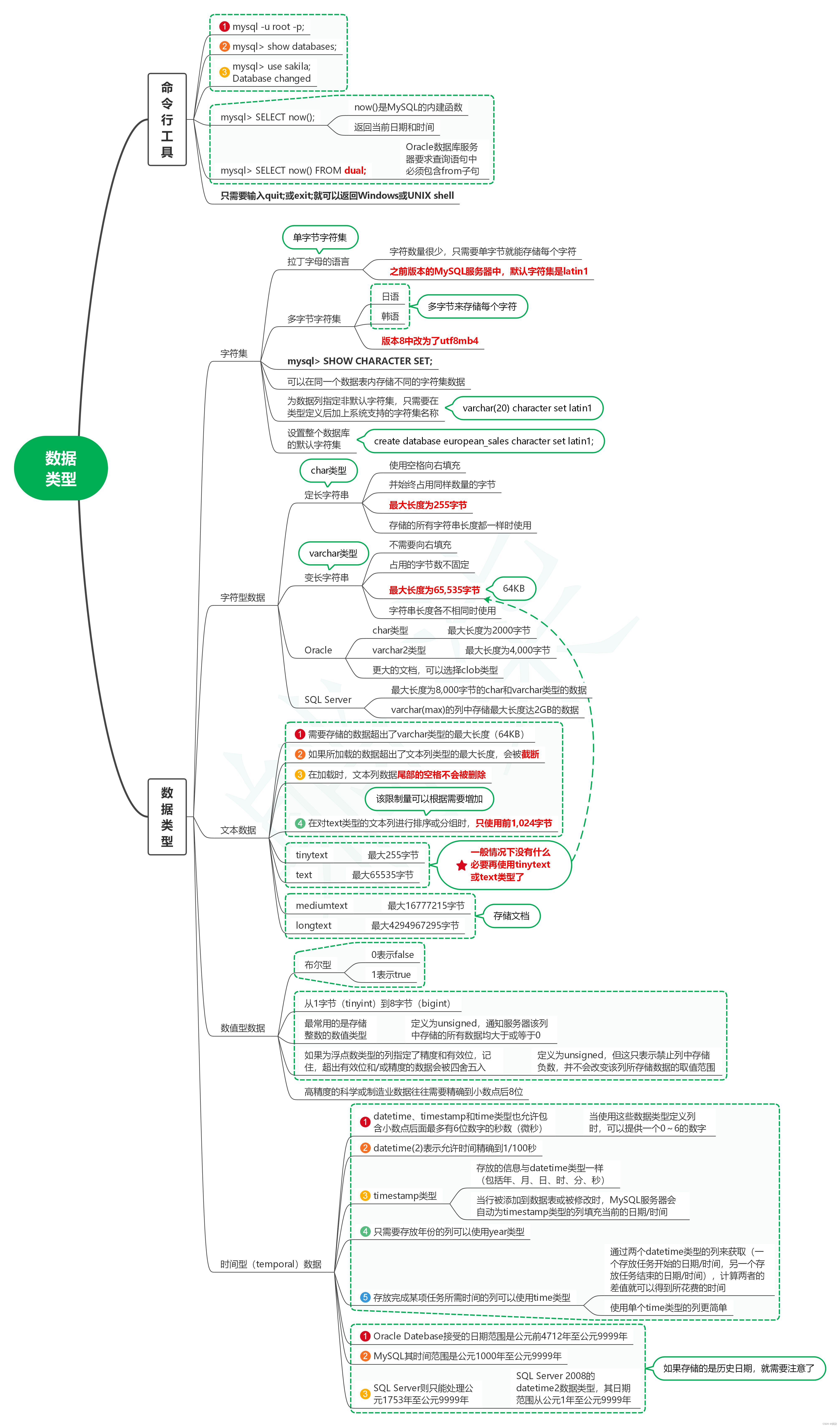
读SQL学习指南(第3版)笔记02_数据类型
1. 命令行工具 1.1. mysql -u root -p; 1.2. mysql> show databases; 1.3. mysql> use sakila; 1.4. mysql> SELECT now(); 1.4.1. now()是MySQL的内建函数 1.4.2. 返回当前日期和时间 1.5. mysql> SELECT now() FROM dual…...
易思智能物流无人值守系统文件上传漏洞复现
0x01 产品简介 易思无人值守智能物流系统是一款集成了人工智能、机器人技术和物联网技术的创新产品。它能够自主完成货物存储、检索、分拣、装载以及配送等物流作业,帮助企业实现无人值守的智能物流运营,提高效率、降低成本,为现代物流行业带…...

git获取远端分支和merge
要将远程分支拉取到本地,你可以使用以下命令: 1. 首先,使用git fetch命令从远程仓库获取最新的分支信息: git fetch origin 这个命令将会将远程仓库origin的分支信息下载到本地。 2. 接下来,可以使用git checkout命…...
linux-进程
文章目录 1.先谈硬件冯诺依曼体系结构 2.再谈软件操作系统什么是操作系统?为什么要有操作系统?如何管理?系统调用 3.再谈进程那么具体Linux是怎么做的?指令 ps ajx 查看所有进程 非实时top 实时查看进程 相当于任务管理器ls /proc 内存级进程…...

整数数组区间的插入与删除
相似题参考: 56. Merge Intervals - 力扣(LeetCode)合并区间 57. 插入区间 - 力扣(LeetCode) 1272. 删除区间 package Jerry;import org.junit.Assert; import org.junit.Test;import java.util.ArrayList; import…...
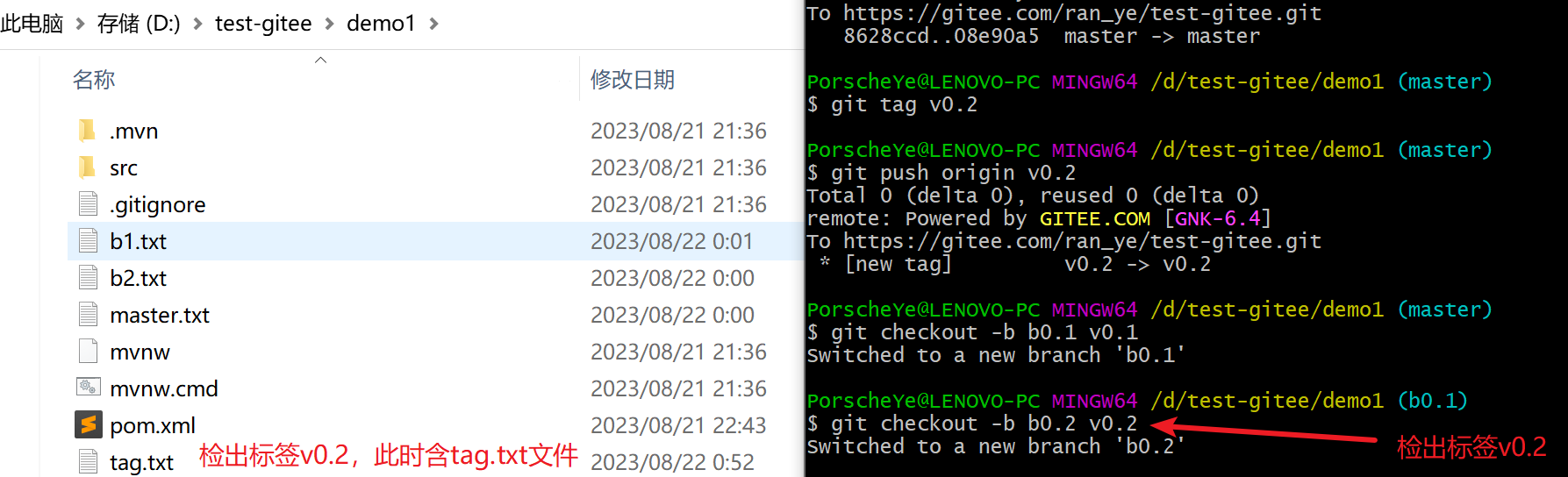
Git标签
Git 中的标签,指的是某个分支某个特定时间点的状态(静态)。通过标签,可以很方便的切换到标记时的状态。 比较有代表性的是人们会使用这个功能来标记发布结点 (v1.0、v1.2等)。 下面是myatis-plus的标签: 1 标签相关命令 命令作用git tag查看标签&…...
BarCodeWiz ActiveX Control Crack
BarCodeWiz ActiveX Control Crack BarcodeWiz ActiveX Control–只需单击按钮即可将所有基本条形码类型添加到Microsoft Office中。在Microsoft Word中,创建单独的条形码、标签页或合并文档。在Microsoft Excel中,选择单元格范围并自动将每个单元格转换…...
group_by报错的处理方法)
mysql高版本(8.0+)group_by报错的处理方法
mysql高版本8.0 group_by报错的处理方法 1. 原因2. 处理方法2.1 临时方法,重启后失效2.2 修改配置my.ini文件 1. 原因 这个错误一般发生在mysql 5.7以及 5.7以上的版本中,其原因是mysql的默认配置中,sql_mode“ONLY_FULL_GROUP_BY” 这个配置严格执行了 ‘SQL92标准…...

Java 下载压缩zip
Java压缩zip /*** 下载压缩包** param instId 实例id* param response 响应* author 梁伟浩* date 2023-08-21*/GetMapping("/downloadZip")ApiOperation(value "下载压缩包")ApiImplicitParam(name "instId", value "实例id", r…...
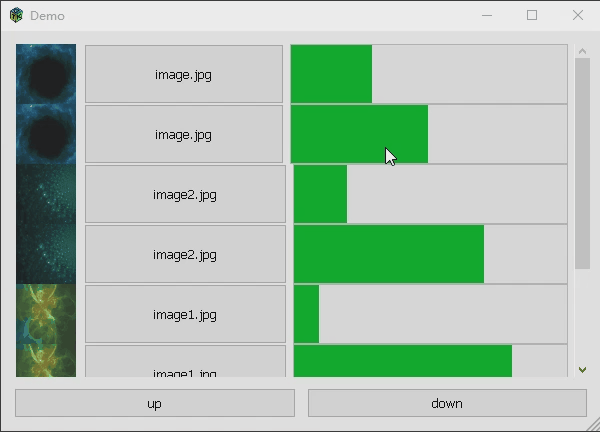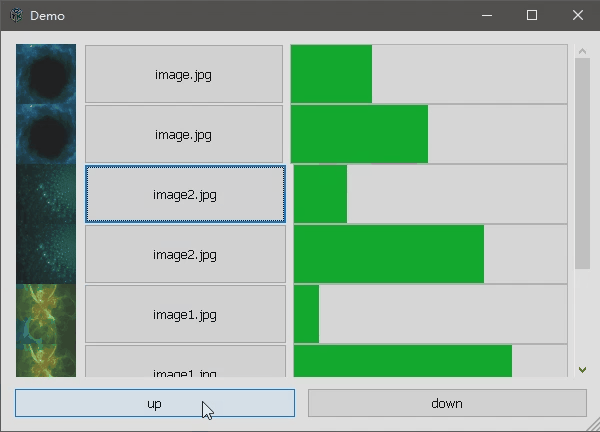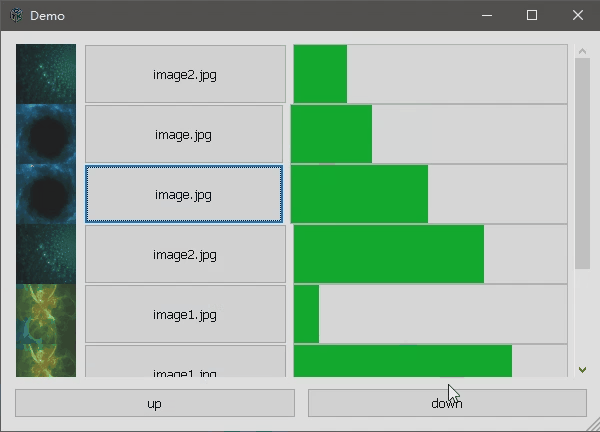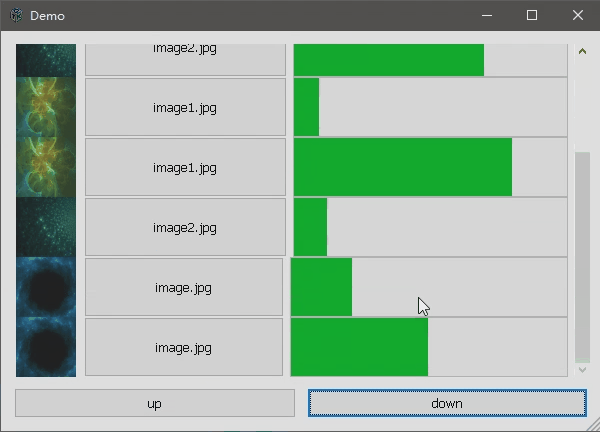
GTK3实现自定义列表
使用gtk,如果想自己定义列表,思路可以将每个列表项作为一个hbox,整个列表是一个vbox。通过对容器动态的添加删除,实现列表操作,同时添加任何自己所需要的控件。 下面的例子是实现一个显示图片、按钮和进度条的列表,并且进行上移下移,具有添加和删除列表项功能但没有演示…...

Go语言基础之数组
Array(数组) 数组是同一种数据类型元素的集合。 在Go语言中,数组从声明时就确定,使用时可以修改数组成员,但是数组大小不可变化。 基本语法: // 定义一个长度为3元素类型为int的数组a var a [3]int数组定义: var 数…...

信息安全从业者考试认证大全
证书是IT从业者知识水平能力的一个体现,考证同时也是拓展自身知识的一个方法。近年来,安全行业风生水起,各种认证层出不穷,眼花缭乱。这里不对任何一个证书做评价,只是做出介绍,在国内,对任何事…...

详解react 15~18新增特性
React 15.x 版本的新增特性: 创建组件类:在 React 15 中,可以使用 createClass 方法来创建组件类。这个方法允许你定义组件的生命周期方法、渲染函数以及其他功能。 PropTypes:React 15 引入了 PropTypes,它是一种用于…...
)
SpringBoot整合FFmpeg进行视频分片上传(Linux)
SpringBoot整合FFmpeg进行视频分片上传(Linux) 上传的核心思路: 1.将文件按一定的分割规则(静态或动态设定,如手动设置20M为一个分片),用slice分割成多个数据块。 2.为每个文件生成一个唯一标识…...
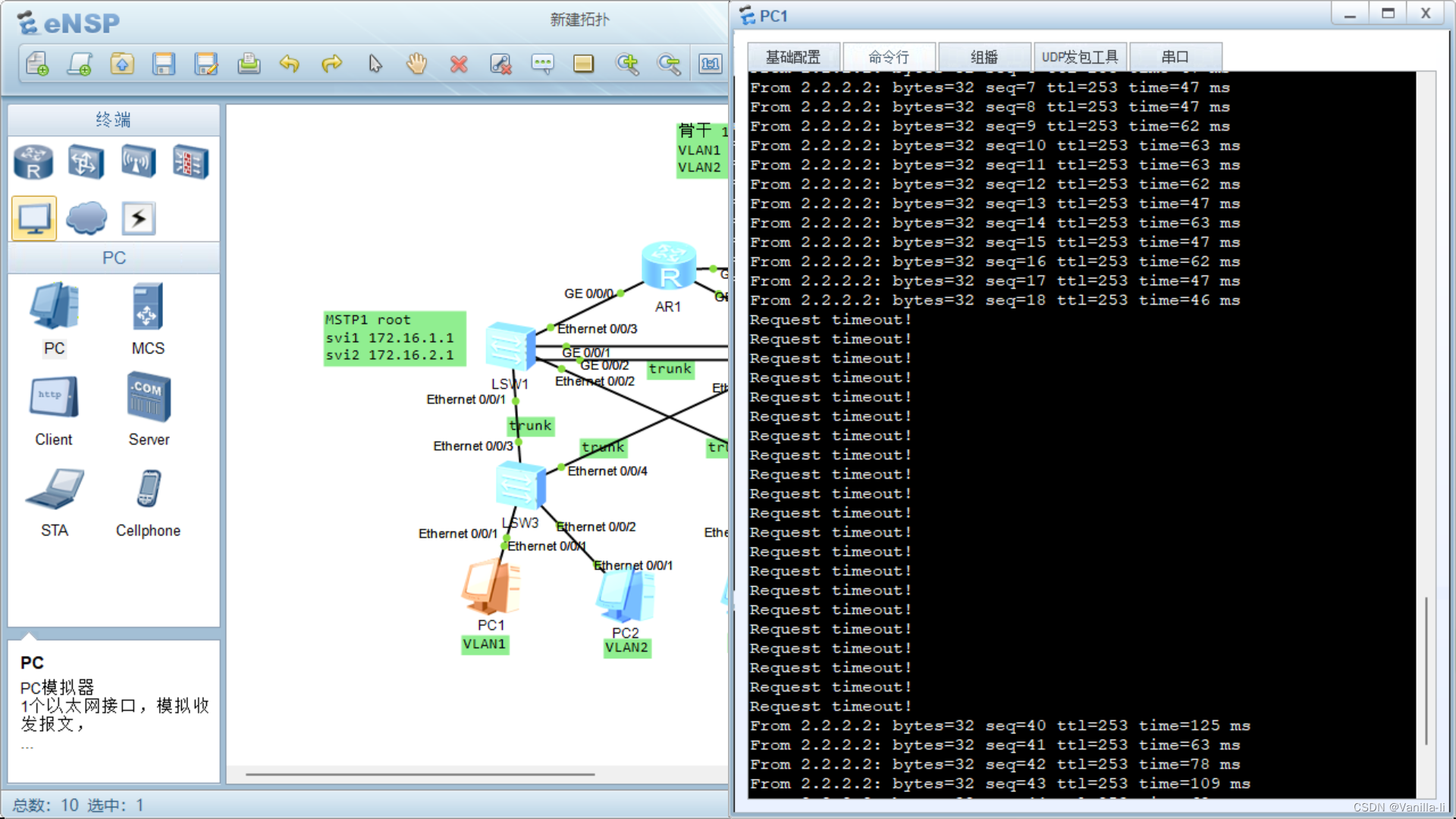
eNSP综合小实验:VRRP、MSTP、Eth-Trunk、NAT、DHCP等技术应用
完成下图要求: 拓扑图: 配置命令: 由于交换机日志太多不便于复制,所以就复制命令。大概步骤如下: 第一步先分配IP地址,在sw1和sw2上创建VLAN100用于e0/0/3口配IP,在sw1、sw2、sw3、sw4上创建VL…...

正中优配:尾盘拉升的股票第二天的走势?
尾盘拉升是指买卖日快结束时股票价格呈现上涨的状况。关于许多投资者来说,这一般是好事情,因为它可认为他们带来更高的收益。但是,人们常常会问尾盘拉升的股票第二天的走势怎么。本文将从多个角度进行剖析。 首要,咱们需求认识到这…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

