如何使用数学将 NumPy 函数的性能提高 50%

一、说明
2D 傅里叶变换是本世纪最重要的计算机科学算法之一。它已在我们的日常生活中得到应用,从Instagram过滤器到MP3文件的处理。
普通用户最常用的实现,有时甚至是在不知不觉中,是 NumPy 的改编。然而,尽管它很受欢迎,但他们的算法并不是最有效的。通过一些简单的操作和 2015 年的一篇文章,我们在性能上击败了 NumPy 算法 30-60%。当前实现的核心问题是一个简单的事实,即它最初是从性能弱算法派生的。
二、NumPy实现的算法
从本质上讲,NumPy实现的算法将常规的一维FFT依次应用于二维,这显然不能成为最优解。
相反,在2015年,两位俄罗斯科学家提出了他们的算法版本,将一维蝶蝶变换的想法应用于二维信号。我们通过添加我们的想法有效地实现了他们的基本算法概念。
在构建了本文中的朴素算法后,我们继续进行优化,如下所示:
void _fft2d( /* Square matrix of size N */ ) {// base case {if (N == 1) return;// } base case int n = N >> 1;/* pseudo code {...Creating 4 temprorary matrices here...// X(x, y, i, j)// x, y -- indexing over temporary submatricies// i, j -- indexing over rows, columns in each submatrix_fft2d(&X(0, 0), root * root, ...);_fft2d(&X(0, 1), root * root, ...);_fft2d(&X(1, 0), root * root, ...);_fft2d(&X(1, 1), root * root, ...);} pseudo code */for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {auto x00 = X(0, 0, i, j);auto x10 = X(1, 0, i, j) * /* W[i] */;auto x01 = X(0, 1, i, j) * /* W[j] */;auto x11 = X(1, 1, i, j) * /* W[i] * W[j] */;X(0, 0, i, j) = x00 + x10 + x01 + x11;X(0, 1, i, j) = x00 + x10 - x01 - x11;X(1, 0, i, j) = x00 - x10 + x01 - x11;X(1, 1, i, j) = x00 - x10 - x01 + x11;}}
}任何递归算法都可以通过增加基本情况的大小来增强。以下是我们的处理方式:
void _fft2d( /* Square matrix of size N */ ) {// base case {if (N == 1) return;if (N == 2) {
#define Y(y, x) (V[(y)*rowsize + (x)])auto x00 = Y(0, 0);auto x10 = Y(1, 0);auto x01 = Y(0, 1);auto x11 = Y(1, 1);Y(0, 0) = x00 + x10 + x01 + x11;Y(0, 1) = x00 + x10 - x01 - x11;Y(1, 0) = x00 - x10 + x01 - x11;Y(1, 1) = x00 - x10 - x01 + x11;return;}// } base case // ...
}
进一步的逻辑步骤是消除在每个递归步骤中创建四个不必要的临时子矩阵,而支持单个子矩阵。为此,我们使用了 algorithmica 文章中的概念,并将其修改为二维矩阵。此功能还有助于我们减少不必要的分配并增加缓存命中次数。
// Computing values for rev_bits[n]
auto revbits = [](size_t *v, size_t n) {int lg_n = log2(n);forn(i, n) {int revi = 0;forn(l, lg_n) revi |= ((i >> l) & 1) << (lg_n - l - 1);v[i] = revi;}
};size_t *rev_n = new size_t[N], *rev_m = new size_t[M];
revbits(rev_n, N), revbits(rev_m, M); // Transforming matrix
forn(i, N) {int rev_i = rev_n[i];forn(j, M) {if ((i < rev_i) || ((i == rev_i) && (j < rev_m[j])))std::swap(V[i * M + j], V[rev_i * M + rev_m[j]]);}
}我们的下一个挑战是预先计算团结的根源:
int mxdim = std::max(N, M);
const int lg_dim = log2(mxdim);
auto W = new fft_type[mxdim];
auto rooti = std::polar(1., (inverse ? 2 : -2) * fft::pi / mxdim);// Computing look-up matrix for roots
auto cur_root = rooti;
W[0] = 1;
forn (i, mxdim - 1) W[i + 1] = W[i] * cur_root;我们怎么能用这样的数组过关?让我们注意到,在朴素实现中,在初始递归步骤中,我们经过一个根的数组。我们还传递到下一个递归级别,即此根的平方(W[2])。在下一个递归级别,我们传递相同的幂数组,但以 2 为增量。从这个观察中,我们可以推导出,在第 i 个递归级别上,我们将通过数组 W 的步骤是 2ⁱ。
在此阶段,我们收到以下代码:
void _fft2d(fft_type *__restrict__ V,size_t N,size_t rowsize,fft_type *__restrict__ W,int step) {// base case {if (N == 1) return;if (N == 2) {
#define Y(y, x) (V[(y)*rowsize + (x)])auto x00 = Y(0, 0);auto x10 = Y(1, 0);auto x01 = Y(0, 1);auto x11 = Y(1, 1);Y(0, 0) = x00 + x10 + x01 + x11;Y(0, 1) = x00 + x10 - x01 - x11;Y(1, 0) = x00 - x10 + x01 - x11;Y(1, 1) = x00 - x10 - x01 + x11;return;}// } base case int n = N >> 1;#define X(y, x, i, j) (V[((y)*n + (i)) * rowsize + ((x)*n) + j])
#define params n, rowsize, W, (step << 1)_fft2d(&X(0, 0, 0, 0), params);_fft2d(&X(0, 1, 0, 0), params);_fft2d(&X(1, 0, 0, 0), params);_fft2d(&X(1, 1, 0, 0), params);for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {auto x00 = X(0, 0, i, j);auto x10 = X(1, 0, i, j) * W[step * i];auto x01 = X(0, 1, i, j) * W[step * j];auto x11 = X(1, 1, i, j) * W[step * (i + j)];X(0, 0, i, j) = x00 + x10 + x01 + x11;X(0, 1, i, j) = x00 + x10 - x01 - x11;X(1, 0, i, j) = x00 - x10 + x01 - x11;X(1, 1, i, j) = x00 - x10 - x01 + x11;}}
}原始算法还有另一个明显的缺点——它只处理维度等于 2 次方的平方矩阵。使用一些简单的修改,我们可以将其扩展到矩形矩阵。
void _plan(fft_type *__restrict__ V,size_t N,size_t M,size_t rowsize,fft_type *__restrict__ W,int step_i,int step_j) {// Computing square matrixif (N == M) _fft2d(V, N, rowsize, W, step_i);// Performing vertical splitelse if (N > M) {int n = N >> 1;
#define Y(y, i, j) (V[((y)*n + (i)) * rowsize + j])
#define params n, M, rowsize, W, (step_i << 1), step_j_plan(&Y(0, 0, 0), params);_plan(&Y(1, 0, 0), params);forn (i, n) {forn (j, M) {auto y00 = Y(0, i, j);auto y10 = Y(1, i, j) * W[i * step_i];Y(0, i, j) = y00 + y10;Y(1, i, j) = y00 - y10;}}// Performing horizontal split} else { /* ...Analogical approach... */ }
}值得一提的是,NumPy在其算法中在FFT下进行了额外的分配,将其中的类型带到了np.complex128;如果我们避免这一步,我们可以获得大约 10% 的优势。我们最终也实现了多线程。
作为可视化表示,我们可以提供带有运行时的表格,还可以提供显示我们关于 NumPy 的工作效率的图表:
结果表

三、结论
俄罗斯数学家修改后的算法在效率方面超过了NumPy引擎盖下的“行和列”。一些逻辑操作,例如基本大小写增加,显着提高了我们的优化。
至关重要的是,我们在实现过程中执行的步骤也可以用于其他算法,这在未来可能对您有所帮助。同样值得注意的是,虽然我们已经做出了坚实的努力,但仍然可以通过添加不同大小的填充矩阵来加强实现。这篇文章旨在分享源代码,这可能有助于改进各种项目中转换的计算。
存储库链接可以在下面找到,或者您也可以使用终端直接导入包:
pip3 install git+https://github.com/2D-FFT-Project/2d-fft参考资源:
包含源代码的存储库
- FFT, 算法
- 二维快速傅里叶变换:Cooley-Tukey算法模拟中的蝴蝶,V. S. Tutatchikov为IEEE,2016年
亚历山大·莱文
相关文章:

如何使用数学将 NumPy 函数的性能提高 50%
一、说明 2D 傅里叶变换是本世纪最重要的计算机科学算法之一。它已在我们的日常生活中得到应用,从Instagram过滤器到MP3文件的处理。 普通用户最常用的实现,有时甚至是在不知不觉中,是 NumPy 的改编。然而,尽管它很受欢迎…...
| 社情民意调查的内容)
群狼调研(长沙政策第三方评估)| 社情民意调查的内容
本文由群狼调研(长沙社会舆情调查)出品,欢迎转载,请注明出处。社情民意调查旨在捕捉公众对各种社会问题的态度、意见和看法,社情民意调查的内容通常包括以下几个方面: 1. 社会热点问题:针对当前社会热点问题进行调查&…...
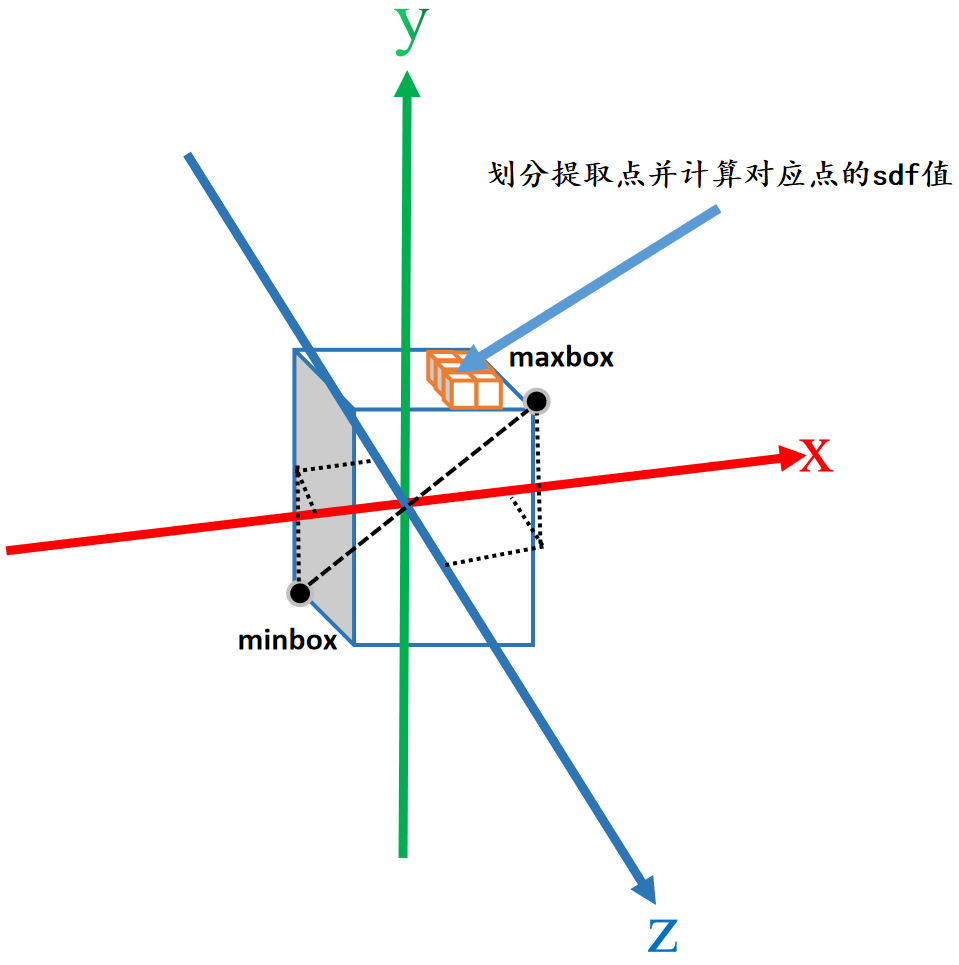
【三维重建】【深度学习】NeuS代码Pytorch实现--测试阶段代码解析(上)
【三维重建】【深度学习】NeuS代码Pytorch实现–测试阶段代码解析(上) 论文提出了一种新颖的神经表面重建方法,称为NeuS,用于从2D图像输入以高保真度重建对象和场景。在NeuS中建议将曲面表示为有符号距离函数(SDF)的零级集,并开发一种新的体绘…...
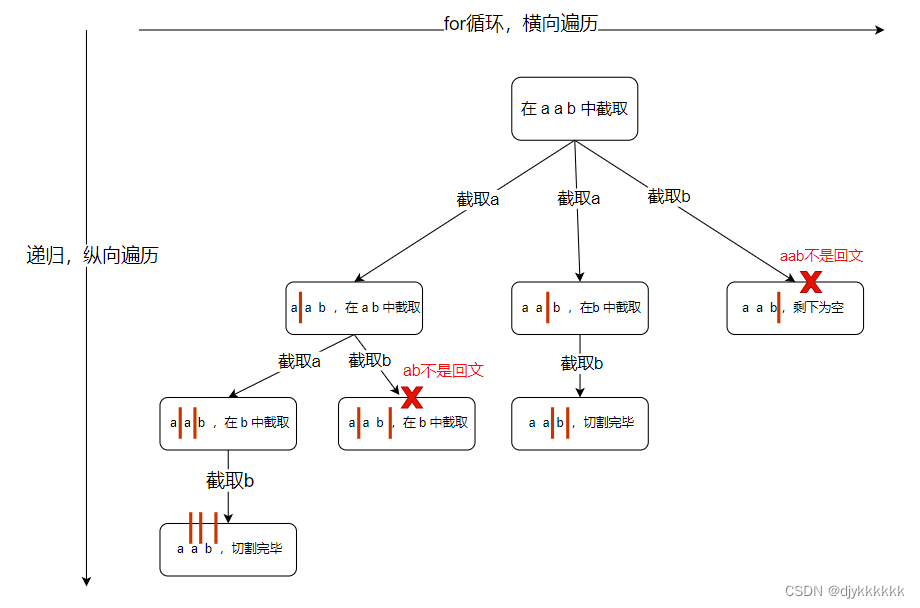
day-24 代码随想录算法训练营(19)回溯part01
77.组合 思路一:回溯相当于枚举,所以我们遍历1-n的每一个数字,然后在遍历第i位的同时递归出第i1~n位的组合结果,跟树的形式相似。 如上图所示,当长度为k时,即退出递归可对遍历到第i位以及剩下位数与k进行比…...

Redis之SYNC与PSYNC命令
一、复制SYNC与PSYNC 在Redis主从架构中,主要有以下两种情形需要进行数据同步 (1)当新的服务器执行slave of 命令,成为主服务器的从服务器。这时候从服务器会向主服务器发送SYNC命令,请求全量同步数据,主服…...

共创无线物联网数字化新模式|协创数据×企企通采购与供应链管理平台项目成功上线
近日,全球无线物联网领先者『协创数据技术股份有限公司』(以下简称“协创数据”)SRM采购与供应链项目全面上线,并于近日与企企通召开成功召开项目上线总结会。 基于双方资源和优势,共同打造了物联网特色的数字化采购供…...

【深入理解jvm读书笔记】jvm如何进行内存分配
jvm如何进行内存分配 内存分配方式内存分配方式的选择并发场景下的内存分配内存空间的初始化构造函数 内存分配方式 指针碰撞空闲列表 指针碰撞法: 假设Java堆中内存是绝对规整的,所有被使用过的内存都被放在一边,空闲的内存被放在另一边&a…...
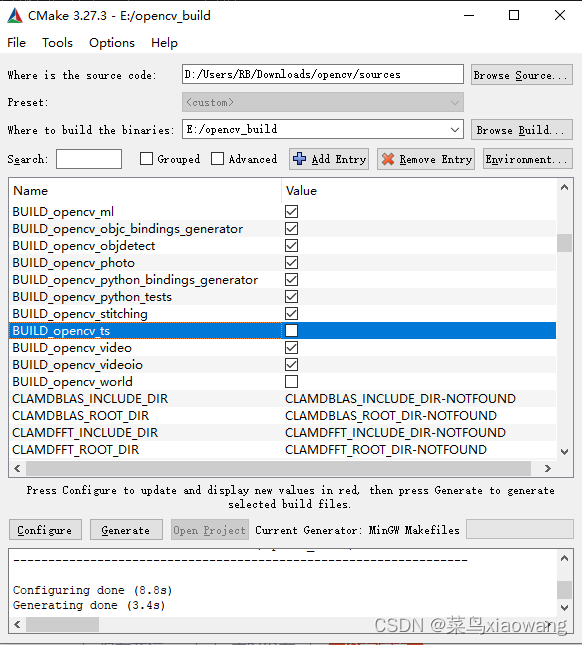
OpenCV使用CMake和MinGW-w64的编译安装
OpenCV使用CMake和MinGW-w64的编译安装中的问题 问题:gcc: error: long: No such file or directory** C:\PROGRA~2\Dev-Cpp\MinGW64\bin\windres.exe: preprocessing failed. modules\core\CMakeFiles\opencv_core.dir\build.make:1420: recipe for target ‘modul…...
亚马逊买家怎么留评
亚马逊买家可以按照以下步骤在购买后留下产品评价: 1、登录亚马逊账户:首先,在网页浏览器中打开亚马逊网站,登录你的亚马逊账户。 2、找到订单:在页面上找到并点击你购买过的商品的"我的订单"或"订单…...
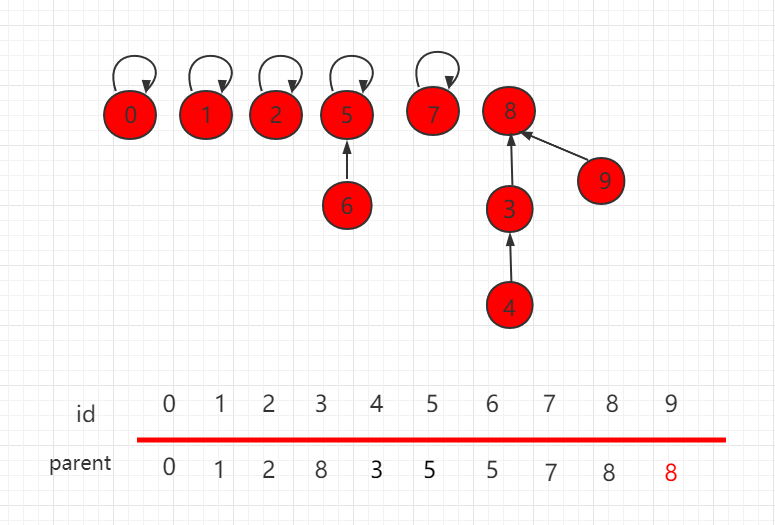
并查集 size 的优化(并查集 size 的优化)
目录 并查集 size 的优化 Java 实例代码 UnionFind3.java 文件代码: 并查集 size 的优化 按照上一小节的思路,我们把如下图所示的并查集,进行 union(4,9) 操作。 合并操作后的结构为: 可以发现,这个结构的树的层相对…...
Qt关于hex转double,或者QByteArray转double
正常的00 ae 02 33这种类型的hex数据类型可以直接通过以下代码进行转换 double QDataConversion::hexToDouble(QByteArray p_buf) {double retValue 0;if(p_buf.size()>4){QString str1 byteArrayToHexStr(p_buf.mid(0,1));QString str2 byteArrayToHexStr(p_buf.mid(1,…...
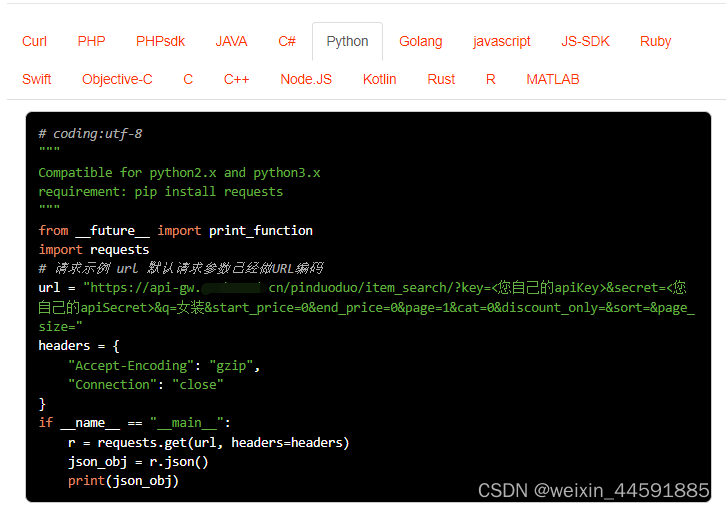
Java“牵手”根据关键词搜索(分类搜索)拼多多商品列表页面数据获取方法,拼多多API实现批量商品数据抓取示例
拼多多商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取拼多多商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问拼多多商城的网页来获取商品列表和详情信息。以下是两种常用方…...

Linux相关知识点
Linux是什么? Linux是一套免费使用和自由传播的类Unix操作系统,是一个基于POSIX和UNIX的多用户、多任务、支持多线程和多CPU的操作系统。它能运行主要的UNIX工具软件、应用程序和网络协议。它支持32位和64位硬件。 Linux内核 是一个Linux系统的内核&…...

常见的的数据结构
数组(Array):一组按顺序排列的元素的集合,可以通过索引访问和修改元素。 链表(Linked List):由一系列节点组成的数据结构,每个节点包含数据和指向下一个节点的指针。 栈࿰…...

专业心理咨询师助你轻装上阵,向内耗说不!
引言 身为技术人,你是否经常感觉自己被掏空了精力,行动力不佳?又或者觉得自己的工作没有成就和意义,工作状态持续不佳?你是否总有一种无法消除的疲惫?即使没有学习、工作,而是选择看剧、刷短视频…...

Ubuntu安装mysql5.7
目录 1. 更新系统软件包2. 安装MySQL 5.73. 启动MySQL 服务4. 设置MySQL root 密码5. 验证MySQL 安装6. 启用远程访问7. 创建新用户8. 为新用户授予权限9. mysql命令 以Ubuntu 18.04系统为例,安装MySQL 5.7。操作步骤如下: 1. 更新系统软件包 sudo apt…...

vue2,使用element中的Upload 上传文件,自定义上传http-request上传,上传附件支持多选,多个文件只发送一次请求,代码里有注释
复制直接使用,组件根据multiple是否多选来返回附件内容,支持多选就返回数据附件,则返回一个附件对象。 //uploadFiles.vue<template><div><el-uploadclass"avatar-uploader"action"#":accept"accep…...

flutter定位简单工具类
import package:permission_handler/permission_handler.dart;class PermissionUtil {/// 获取用户定位权限static Future<bool> getLocationStatus() async {Map<Permission, PermissionStatus> statuses await [Permission.location,].request();return statuse…...
java请求SAP系统,发起soap的xml报文,实体类转换,idea自动生成教程
1、将接口的网页地址,右键保存,然后修改文件后缀为wsdl文件 2、idea全局搜索 wsdl,找到自动转换javabean插件: 3、点击后,选择下载改完后缀的文件(选择): 4、将无用的class文件删除掉 5、请求sap的地址为…...
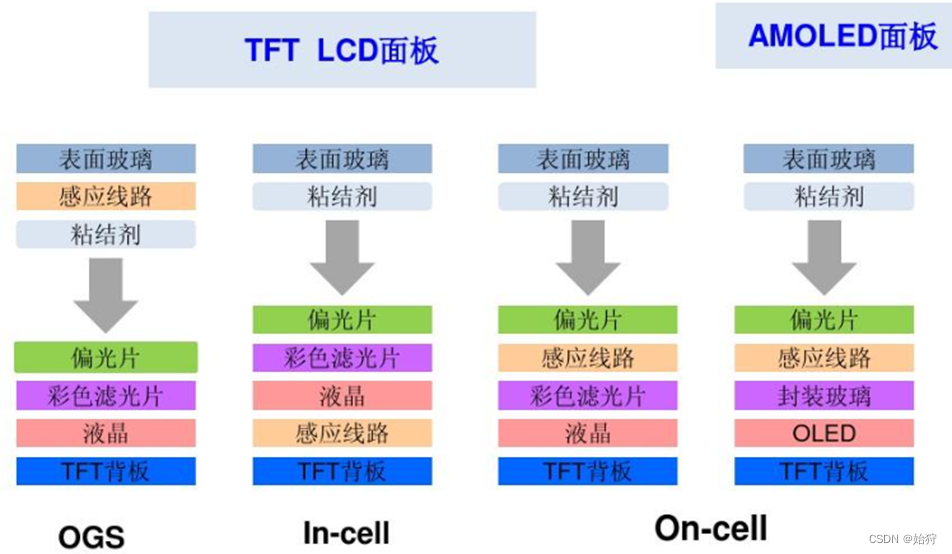
不同屏幕的触控技术
不同显示屏的触控技术原理有所不同。触摸屏的基本原理是,用手指或其他物体触摸安装在显示器前端的触摸屏时,所触摸的位置(以坐标形式)由触摸屏控制器检测,并通过接口(如RS-232串行口)送到CPU,从而确定输入的信息。 目前市场上常…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
