Leetcode---359周赛
题目列表
2828. 判别首字母缩略词
2829. k-avoiding 数组的最小总和
2830. 销售利润最大化
2831. 找出最长等值子数组
一、判断首字母缩略词

纯模拟,代码如下
class Solution {
public:bool isAcronym(vector<string>& words, string s) {string tmp;for(auto & x:words)tmp+=x[0];return tmp==s;}
};二、k-avoiding数组的最小和


根据题目所给的数据范围,我们甚至可以将和为k的数据对全部求出来,然后一个个筛选,但是没必要,我们只要从小到大枚举元素,将枚举过的元素记录起来,当遇到能匹配的元素时跳过就行,直到选满n个元素(有点贪心的意思在里面)
class Solution {
public:int minimumSum(int n, int k) {set<int> s;int sum=0;for(int i=1;n;i++){if(s.find(k-i)==s.end()){s.insert(i);sum+=i;n--;}}return sum;}
};或者直接推导出数学公式,代码如下(利用等差数列求和公式)
class Solution {
public:int minimumSum(int n, int k) {int m=min(k/2,n);return m*(m+1)/2+(k+k+(n-m-1))*(n-m)/2;}
};三、销售利润最大化

这题相信有人一看到最大化就直接去想贪心了,但是这题的贪心策略是不确定的,因为它是由区间和价格共同影响决定的,好,既然贪心不行,我们就要去想想动态规划
1.dp数组有几个维度,含义是什么?(最重要的一步,后面几个问题都是围绕这个问题展开的)
根据题目要求,我们定义dp[i]代表前i个房子能获取的最大利润
2.dp数组的递推公式
1)如果不选i这个位置的房子,那么相当于只考虑前i-1个房子,即dp[ i ]=dp[ i - 1 ]
2)如果选i这个位置的房子,那么我们只能选以i为右端点区间的买家,所以前i个房子的最大利润=以i为右端点区间的买家价格+该买家买的左端点之前的房屋最大利润,
即dp[i]=offers[j][2]+dp[offer[j][0] - 1] (j是代表以i为有端点的买家下标)
上诉两种情况取最大值得到dp[i]
3.dp数组的初始化
dp[0]=0,即前0个房子的最大利润是0,前0个房子也就是没有房子可以选,故利润为0
动态规划问题总结:关键是将上面三个问题搞明白,尤其是第一个问题,它将直接关乎另外两个问题的思考难度和方法的正确性
代码如下
class Solution {
public:int maximizeTheProfit(int n, vector<vector<int>>& offers) {//将右端点相同的买家分类记录vector<vector<int>> v(n);for(int i=0;i<offers.size();i++)v[offers[i][1]].push_back(i);int dp[n+1];dp[0]=0;//数组初始化for(int i=1;i<=n;i++){dp[i]=dp[i-1];//不选第i个房子(i和房子下标差1)for(auto& x:v[i-1]){//选第i个房子,下标为i-1dp[i]=max(dp[i],dp[offers[x][0]]+offers[x][2]);//这里的offers中记录的左端点是下标,不用-1}}return dp[n];}
};四、找到最长等值子数组

这题找最长等值子数组,即将不同数字为等值的最大值都算出来,取最大值即可
不同数字的最大值计算用双指针(滑动窗口)
代码如下
class Solution {
public:int longestEqualSubarray(vector<int>& nums, int k) {int n=nums.size();vector<vector<int>> v(n+1);for(int i=0;i<n;i++)v[nums[i]].push_back(i);int ans=1;for(int i=1;i<=n;i++){for(int left=0,right=0;right<v[i].size();right++){while(v[i][right]-v[i][left]-(right-left)>k)left++;ans=max(ans,right-left+1);}}return ans;}
};相关文章:

Leetcode---359周赛
题目列表 2828. 判别首字母缩略词 2829. k-avoiding 数组的最小总和 2830. 销售利润最大化 2831. 找出最长等值子数组 一、判断首字母缩略词 纯模拟,代码如下 class Solution { public:bool isAcronym(vector<string>& words, string s) {string tmp…...

Keras三种主流模型构建方式:序列模型、函数模型、子类模型开发实践,以真实烟雾识别场景数据为例
Keras和PyTorch是两个常用的深度学习框架,它们都提供了用于构建和训练神经网络的高级API。 Keras: Keras是一个高级神经网络API,可以在多个底层深度学习框架上运行,如TensorFlow和CNTK。以下是Keras的特点和优点: 优点…...

objective-v 获取iPhone系统当前时间字符串适配12小时制和24小时制
我们最开始获取系统当前时间,如下,这种方式存在一个问题,当iPhone关闭了24小时制时,获取的时间格式是:iPhone11上:20230822下午210568760;iPhone7 plus上:2023082240043851 PM&#…...

并查集及其简单应用
文章目录 一.并查集二.并查集的实现三.并查集的基本应用 一.并查集 并查集的逻辑结构:由多颗不相连通的多叉树构成的森林(一个这样的多叉树就是森林的一个连通分量) 并查集的元素(树节点)用0~9的整数表示,并查集可以表示如下: 并查集的物理存储结构:并查集一般采用顺序结构实…...
基于web的服装商城系统java网上购物商店jsp源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 基于web的服装商城系统 系统有1权限:前台…...

.NET Core发布到IIS
项目介绍 1、开发工具Visual Studio 2017,语言C#,SQL SERVER,WIN10 2、本地IIS,手机上或其他用户在和本地在同一个局域网内访问,同时要把防火墙关掉 3、IIS全名Internet Information Services,用来发布网站 先决条件 安…...
Spring的基本概念
前言 Spring 究竟是什么?其实Spring简单来说就是一个包含众多工具方法的IOC容器。 那么什么是IOC呢? IoC Inversion of Control 翻译成中⽂是“控制反转”的意思. 既然Spring 是⼀个IoC(控制反转)容器,重点还在“容…...

设计模式之原型模式
文章目录 一、介绍二、实现步骤三、案例四、应用五、细胞分裂六、改造细胞分裂逻辑七、总结 一、介绍 原型模式属于创建型设计模式,用于创建重复的对象,且同时又保证了性能。 该设计模式的好处是将对象的创建与调用方分离。 其目的就是**根据一个对象…...

正则表达式在网页处理中的应用四则
正则表达式在网页处理中的应用四则 正则表达式(Regular Expression)为字符串模式匹配提供了一种高效、方便的方法。几乎所有高级语言都提供了对正则表达式的支持,或者提供了现成的代码库供调用。本文以ASP环境中常见的处理任务为例,介绍正则表达式的应用技巧。 一、检验密…...

ping使用方法
文章目录 1、Ping的基础知识2、Ping命令详解3、怎样使用Ping这命令来测试网络连通?4、如何用Ping命令来判断一条链路好坏?5、对Ping后返回信息的分析1.Request timed out2.Destination host Unreachable 1、Ping的基础知识 ping命令相信大家已经再熟悉不…...

“心理健康人工智能产学研创新联盟”揭牌成立|深兰科技
8月14日上午,“2023树洞救援年会”在上海举行,会上举行了“心理健康人工智能产学研创新联盟”的签约和揭牌仪式。“树洞行动救援团”创始人深兰科技科学院智能科学首席科学家、荷兰阿姆斯特丹自由大学人工智能系终身教授黄智生,深兰科技集团创…...
FastDFS+Nginx - 本地搭建文件服务器同时实现在外远程访问「端口映射」
文章目录 前言1. 本地搭建FastDFS文件系统1.1 环境安装1.2 安装libfastcommon1.3 安装FastDFS1.4 配置Tracker1.5 配置Storage1.6 测试上传下载1.7 与Nginx整合1.8 安装Nginx1.9 配置Nginx 2. 局域网测试访问FastDFS3. 安装cpolar内网穿透4. 配置公网访问地址5. 固定公网地址5.…...
Mybatis-动态sql和分页
目录 一.什么是Mybatis动态分页 二.mybatis中的动态SQL 在BookMaaper.xml中写sql BookMapper BookBiz接口类 BookBizImpl实现接口类 demo测试类 编辑 测试结果 三.mybatis中的模糊查询 mybatis中的#与$有是什么区别 在BookMapper.xml里面建立三个模糊查询 编辑 …...

基于YOLOV8模型的西红柿目标检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOV8模型的西红柿目标检测系统可用于日常生活中检测与定位西红柿目标,利用深度学习算法可实现图片、视频、摄像头等方式的目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测算法训练数…...
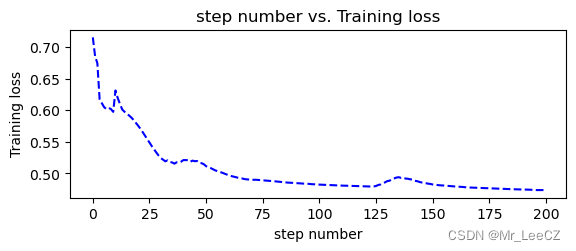
数学建模及数据分析 || 4. 深度学习应用案例分享
PyTorch 深度学习全连接网络分类 文章目录 PyTorch 深度学习全连接网络分类1. 非线性二分类2. 泰坦尼克号数据分类2.1 数据的准备工作2.2 全连接网络的搭建2.3 结果的可视化 1. 非线性二分类 import sklearn.datasets #数据集 import numpy as np import matplotlib.pyplot as…...

数据分析15——office中的Excel基础技术汇总
0、前言: 这部分总结就是总结每个基础技术的定义,在了解基础技术名称和定义后,方便对相关技术进行检索学习。笔记不会详细到所有操作都说明,但会把基础操作的名称及作用说明,可自行检索。本文对于大部分读者有以下作用…...
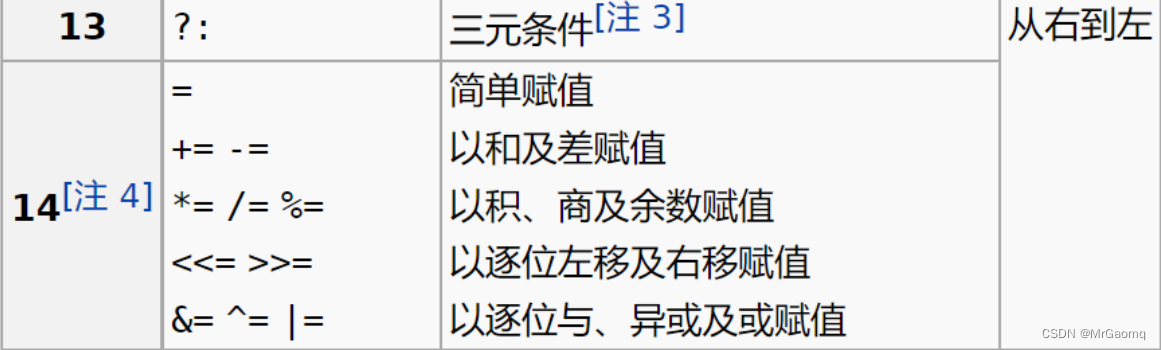
C语言好题解析(四)
目录 选择题一选择题二选择题三选择题四选择题五编程题一 选择题一 已知函数的原型是: int fun(char b[10], int *a); 设定义: char c[10];int d; ,正确的调用语句是( ) A: fun(c,&d); B: fun(c,d); C: fun(&…...

英语——主谓一致
主谓一致是指句子的谓语动词与其主语在数上必须保持一致,一般遵循以下三个原则: 一、语法形式上一致,即单复数形式与谓语要一致。 二、意义上一致,即主语意义上的单复数要与谓语的单复数形式一致。 三、就近以及就远原则,即谓语动词的单复形式取决于最靠近它的词语或者离它…...

属性字符串解析
连续的KV的字符串,每个KV之间用","分隔,V中可嵌套KV的连续字符串结构,例如“ key1value1,key2value2,key3[key4value4,key5value5,key6[key7value7]],key8value8 请编写如下函数,给定字符串,输出嵌套结构的H…...
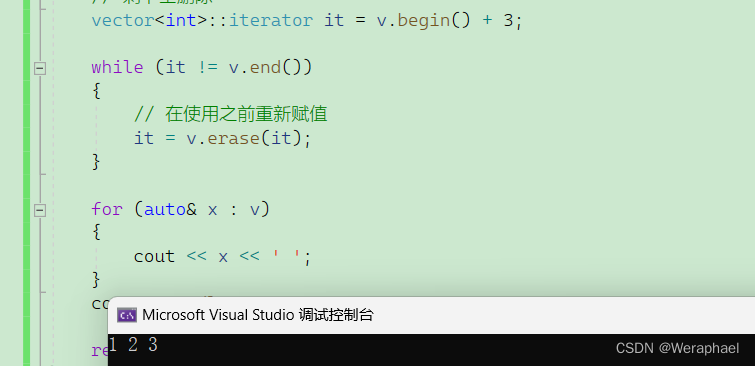
【C++初阶】vector容器
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:C航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
