机器学习笔记之优化算法(十七)梯度下降法在强凸函数的收敛性分析
机器学习笔记之优化算法——梯度下降法在强凸函数的收敛性分析
- 引言
- 回顾:梯度下降法在强凸函数的收敛性
- 二阶可微——梯度下降法在强凸函数的收敛性推论
引言
上一节介绍并证明了:梯度下降法在强凸函数上的收敛速度满足 Q \mathcal Q Q-线性收敛。
本节将介绍:在更强的条件下:函数 f ( ⋅ ) f(\cdot) f(⋅)在其定义域内二阶可微,梯度下降法在 f ( ⋅ ) f(\cdot) f(⋅)上的收敛速度存在什么样的结论。
回顾:梯度下降法在强凸函数的收敛性
关于梯度下降法在 m m m-强凸函数上的收敛性定理表示如下:
条件:
- 函数 f ( ⋅ ) f(\cdot) f(⋅)向下有界,在其定义域内可微,并且 f ( ⋅ ) f(\cdot) f(⋅)是 m m m-强凸函数;
- 关于 f ( ⋅ ) f(\cdot) f(⋅)的梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续;
- 梯度下降法迭代过程中,其步长 α k \alpha_k αk存在明确的约束范围: α k ∈ ( 0 , 2 L + m ) \begin{aligned}\alpha_k \in \left(0,\frac{2}{\mathcal L+ m} \right)\end{aligned} αk∈(0,L+m2);
结论:
数值解序列 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞以 Q \mathcal Q Q-线性收敛的收敛速度收敛于最优数值解 x ∗ x^* x∗。
根据 Q \mathcal Q Q-线性收敛的定义,关于结论的证明可转化为下述公式成立:
∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ a ∈ ( 0 , 1 ) k = 1 , 2 , 3 , ⋯ \begin{aligned}\frac{||x_{k+1} - x^*||}{||x_k - x^*||} \leq a \in (0,1) \quad k = 1,2,3,\cdots\end{aligned} ∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣≤a∈(0,1)k=1,2,3,⋯
其证明过程见上一节——梯度下降法在强凸函数上的收敛性证明,这里不再赘述。最终我们得证:
∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ 1 − α ⋅ 2 L m L + m \begin{aligned}\frac{||x_k - \alpha \cdot \nabla f(x_k) - x^*||}{||x_k- x^*||} \leq \sqrt{1 - \alpha \cdot \frac{2\mathcal L m}{\mathcal L + m}}\end{aligned} ∣∣xk−x∗∣∣∣∣xk−α⋅∇f(xk)−x∗∣∣≤1−α⋅L+m2Lm
并有: 1 − α ⋅ 2 L m L + m ∈ ( 0 , 1 ) \begin{aligned}\sqrt{1 - \alpha \cdot \frac{2\mathcal L m}{\mathcal L + m}}\end{aligned} \in (0,1) 1−α⋅L+m2Lm∈(0,1)恒成立。
二阶可微——梯度下降法在强凸函数的收敛性推论
-
如果函数 f ( ⋅ ) f(\cdot) f(⋅)向下有界,并且 f ( ⋅ ) f(\cdot) f(⋅)是 m m m-强凸函数,在其定义域内二阶可微。在凸函数 VS \text{VS} VS强凸函数中介绍的:根据强凸函数的二阶条件, f ( ⋅ ) f(\cdot) f(⋅)对应的 Hessian Matrix ⇒ ∇ 2 f ( ⋅ ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(\cdot) Hessian Matrix⇒∇2f(⋅)存在,并且必然有:
其中I \mathcal I I是单位矩阵。
∇ 2 f ( ⋅ ) ≽ m ⋅ I \nabla^2 f(\cdot) \succcurlyeq m \cdot \mathcal I ∇2f(⋅)≽m⋅I
也就是说: ∇ 2 f ( ⋅ ) − m ⋅ I ≽ 0 \nabla^2 f(\cdot) - m \cdot \mathcal I \succcurlyeq 0 ∇2f(⋅)−m⋅I≽0,即:矩阵 ∇ 2 f ( ⋅ ) − m ⋅ I \nabla^2 f(\cdot) - m \cdot \mathcal I ∇2f(⋅)−m⋅I是半正定矩阵。 -
继续观察条件:如果梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续,并且 f ( ⋅ ) f(\cdot) f(⋅)二阶可微,则有:
使用拉格朗日中值定理进行表示:∀ x , y ∈ R n , ∃ ξ ∈ ( x , y ) ⇒ ∣ ∣ ∇ 2 f ( ξ ) ∣ ∣ = ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ∣ ∣ x − y ∣ ∣ \begin{aligned}\forall x,y \in \mathbb R^n,\exist \xi \in (x,y) \Rightarrow ||\nabla^2 f(\xi)|| = \frac{||\nabla f(x) - \nabla f(y)||}{||x - y||}\end{aligned} ∀x,y∈Rn,∃ξ∈(x,y)⇒∣∣∇2f(ξ)∣∣=∣∣x−y∣∣∣∣∇f(x)−∇f(y)∣∣
∣ ∣ ∇ 2 f ( ⋅ ) ∣ ∣ ≤ L ||\nabla^2 f(\cdot)|| \leq \mathcal L ∣∣∇2f(⋅)∣∣≤L
将范数符号去掉,可表示为:
− L ⋅ I ≼ ∇ 2 f ( ⋅ ) ≼ L ⋅ I -\mathcal L \cdot \mathcal I \preccurlyeq \nabla^2 f(\cdot) \preccurlyeq\mathcal L \cdot \mathcal I −L⋅I≼∇2f(⋅)≼L⋅I
但又由于 f ( ⋅ ) f(\cdot) f(⋅)是 m m m-强凸函数的性质,因而 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)存在更强的下界: m ⋅ I ≥ − L ⋅ I m \cdot \mathcal I \geq -\mathcal L \cdot \mathcal I m⋅I≥−L⋅I,因而只需认知它的上界即可:
∇ 2 f ( ⋅ ) ≼ L ⋅ I \nabla^2 f(\cdot) \preccurlyeq\mathcal L \cdot \mathcal I ∇2f(⋅)≼L⋅I
也就是说: L ⋅ I − ∇ 2 f ( ⋅ ) ≽ 0 \mathcal L \cdot \mathcal I - \nabla^2 f(\cdot) \succcurlyeq 0 L⋅I−∇2f(⋅)≽0,即:矩阵 L ⋅ I − ∇ 2 f ( ⋅ ) \mathcal L \cdot \mathcal I - \nabla^2 f(\cdot) L⋅I−∇2f(⋅)是半正定矩阵。
将上述两个结论合并,有:
m ⋅ I ≼ ∇ 2 f ( ⋅ ) ≼ L ⋅ I m \cdot \mathcal I\preccurlyeq \nabla^2 f(\cdot) \preccurlyeq \mathcal L \cdot \mathcal I m⋅I≼∇2f(⋅)≼L⋅I
继续观察 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅),由于 ∇ 2 f ( ⋅ ) ≽ m ⋅ I \nabla^2 f(\cdot) \succcurlyeq m\cdot \mathcal I ∇2f(⋅)≽m⋅I且 m > 0 m > 0 m>0,因此 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)自身不仅是一个实对称矩阵,并且还是一个正定矩阵。因而可以对 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)进行特征值分解:
其中 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn表示 Hessian Matrix : [ ∇ 2 f ( ⋅ ) ] n × n \text{Hessian Matrix} :[\nabla^2 f(\cdot)]_{n \times n} Hessian Matrix:[∇2f(⋅)]n×n的 n n n个特征值。而 n n n表示特征空间维数,与 x , y ∈ R n x,y \in \mathbb R^n x,y∈Rn是同一个 n n n。
∇ 2 f ( ⋅ ) = Q Λ Q − 1 = Q ( λ 1 λ 2 ⋱ λ n ) Q − 1 \nabla^2 f(\cdot) = \mathcal Q \Lambda \mathcal Q^{-1} = \mathcal Q \begin{pmatrix} \lambda_1 &\quad&\quad&\quad \\ \quad &\lambda_2& \quad&\quad \\ \quad &\quad& \ddots&\quad \\ \quad & \quad& \quad & \lambda_n \end{pmatrix}\mathcal Q^{-1} ∇2f(⋅)=QΛQ−1=Q λ1λ2⋱λn Q−1
假设对角矩阵 Λ \Lambda Λ中的特征值按照大到小的顺序排列:
在降维——最大投影方差角度中对特征值的大小关系进行描述过。可以将 λ 1 \lambda_1 λ1对应的特征向量视作第一主成分,后续以此类推。
λ m a x = λ 1 ≥ λ 2 ≥ λ 3 ≥ ⋯ ≥ λ n = λ m i n \lambda_{max} = \lambda_1 \geq \lambda_2 \geq \lambda_3 \geq \cdots \geq \lambda_n = \lambda_{min} λmax=λ1≥λ2≥λ3≥⋯≥λn=λmin
- 观察矩阵: ∇ 2 f ( ⋅ ) − m ⋅ I \nabla^2 f(\cdot) - m\cdot \mathcal I ∇2f(⋅)−m⋅I,将特征值分解结果代入,有:
由于单位矩阵I = Q Q − 1 \mathcal I = \mathcal Q \mathcal Q^{-1} I=QQ−1,因此m ⋅ I = Q m Q − 1 m \cdot \mathcal I = \mathcal Q m \mathcal Q^{-1} m⋅I=QmQ−1
∇ 2 f ( ⋅ ) − m ⋅ I = Q Λ Q − 1 − Q m Q − 1 = Q ( λ 1 − m λ 2 − m ⋱ λ n − m ) Q − 1 \nabla^2 f(\cdot) - m\cdot \mathcal I = \mathcal Q \Lambda \mathcal Q^{-1} - \mathcal Q m \mathcal Q^{-1} = \mathcal Q\begin{pmatrix} \lambda_1-m &\quad&\quad&\quad \\ \quad &\lambda_2-m& \quad&\quad \\ \quad &\quad& \ddots&\quad \\ \quad & \quad& \quad & \lambda_n-m \end{pmatrix} \mathcal Q^{-1} ∇2f(⋅)−m⋅I=QΛQ−1−QmQ−1=Q λ1−mλ2−m⋱λn−m Q−1
由于矩阵 ∇ 2 f ( ⋅ ) − m ⋅ I \nabla^2 f(\cdot) - m\cdot \mathcal I ∇2f(⋅)−m⋅I是半正定矩阵,因而必然有:
λ i − m ≥ 0 i = 1 , 2 , ⋯ , n \lambda_i - m \geq 0 \quad i=1,2,\cdots,n λi−m≥0i=1,2,⋯,n
也就是说: λ m i n − m ≥ 0 ⇒ λ m i n ≥ m \lambda_{min} - m \geq 0 \Rightarrow \lambda_{min} \geq m λmin−m≥0⇒λmin≥m - 同理,观察矩阵: L ⋅ I − ∇ 2 f ( ⋅ ) \mathcal L \cdot \mathcal I - \nabla^2 f(\cdot) L⋅I−∇2f(⋅),必然有:
{ L ⋅ I − ∇ 2 f ( ⋅ ) = Q ( L − λ 1 L − λ 2 ⋱ L − λ n ) Q − 1 L − λ i ≥ 0 i = 1 , 2 , ⋯ , m L − λ m a x ≥ 0 ⇒ λ m a x ≤ L \begin{cases} \begin{aligned} & \mathcal L \cdot \mathcal I - \nabla^2 f(\cdot) = \mathcal Q\begin{pmatrix} \mathcal L - \lambda_1 &\quad&\quad&\quad \\ \quad &\mathcal L - \lambda_2& \quad&\quad \\ \quad &\quad& \ddots&\quad \\ \quad & \quad& \quad & \mathcal L - \lambda_n \end{pmatrix} \mathcal Q^{-1} \\ & \mathcal L - \lambda_i \geq 0 \quad i=1,2,\cdots,m \\ & \mathcal L - \lambda_{max} \geq 0 \Rightarrow \lambda_{max} \leq \mathcal L \end{aligned} \end{cases} ⎩ ⎨ ⎧L⋅I−∇2f(⋅)=Q L−λ1L−λ2⋱L−λn Q−1L−λi≥0i=1,2,⋯,mL−λmax≥0⇒λmax≤L
对上述大小关系进行整理,最终有:
0 < m ≤ λ m i n ≤ λ m a x ≤ L 0 < m \leq \lambda_{min} \leq \lambda_{max} \leq \mathcal L 0<m≤λmin≤λmax≤L
回顾上一节——梯度下降法在强凸函数上的收敛性证明过程中,关于辅助函数 G ( ⋅ ) \mathcal G(\cdot) G(⋅)的梯度 ∇ G ( ⋅ ) \nabla \mathcal G(\cdot) ∇G(⋅)满足余强制性时,有如下式子成立:
[ ∇ G ( x ) − ∇ G ( y ) ] T ( x − y ) ≥ 1 L − m ∣ ∣ ∇ G ( x ) − ∇ G ( y ) ∣ ∣ 2 [\nabla \mathcal G(x) - \nabla \mathcal G(y)]^T(x - y) \geq \frac{1}{\mathcal L - m} ||\nabla \mathcal G(x) - \nabla \mathcal G(y)||^2 [∇G(x)−∇G(y)]T(x−y)≥L−m1∣∣∇G(x)−∇G(y)∣∣2
当时我们对 L , m \mathcal L,m L,m之间的大小关系仅限于 L ≥ m \mathcal L \geq m L≥m,但一旦二阶可微的函数 f ( ⋅ ) f(\cdot) f(⋅)被确定,那么对应的 Hessian Matrix ⇒ ∇ 2 f ( ⋅ ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(\cdot) Hessian Matrix⇒∇2f(⋅)以及 λ m a x , λ m i n \lambda_{max},\lambda_{min} λmax,λmin都是被确定的。也就是说:关于常数 L , m \mathcal L,m L,m满足: 0 < m ≤ λ m i n ≤ λ m a x ≤ L 0 < m \leq \lambda_{min} \leq \lambda_{max} \leq \mathcal L 0<m≤λmin≤λmax≤L,才有该函数 f ( ⋅ ) f(\cdot) f(⋅)满足 L \mathcal L L-利普希兹连续,以及 m m m-强凸函数的条件。
如果令: m = λ m i n ; L = λ m a x ; α = 1 L \begin{aligned}m = \lambda_{min};\mathcal L = \lambda_{max};\alpha = \frac{1}{\mathcal L}\end{aligned} m=λmin;L=λmax;α=L1,这相当于对 L \mathcal L L-利普希兹连续、 m m m-强凸函数两个条件进行了更严苛的约束,继续对上述 Q \mathcal Q Q-线性收敛公式: ∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ 1 − α ⋅ 2 L m L + m \begin{aligned}\frac{||x_k - \alpha \cdot \nabla f(x_k) - x^*||}{||x_k- x^*||} \leq \sqrt{1 - \alpha \cdot \frac{2\mathcal L m}{\mathcal L + m}}\end{aligned} ∣∣xk−x∗∣∣∣∣xk−α⋅∇f(xk)−x∗∣∣≤1−α⋅L+m2Lm进行化简:
关于步长变量α \alpha α的取值,我们将L \mathcal L L-利普希兹连续条件下的最优步长 1 L \begin{aligned}\frac{1}{\mathcal L}\end{aligned} L1代入其中。关于最优步长的推导过程详见二次上界引理,这里不再赘述。
0 < 1 L = 2 L + L ≤ 2 L + m L > 0 ; L ≥ m \begin{aligned}0 < \frac{1}{\mathcal L} = \frac{2}{\mathcal L + \mathcal L} \leq \frac{2}{\mathcal L + m} \quad \mathcal L>0;\mathcal L\geq m\end{aligned} 0<L1=L+L2≤L+m2L>0;L≥m由于条件中自身存在关于步长的约束:α ∈ ( 0 , 2 L + m ) \begin{aligned}\alpha \in \left(0,\frac{2}{\mathcal L + m}\right)\end{aligned} α∈(0,L+m2),需要观察一下1 L \begin{aligned}\frac{1}{\mathcal L}\end{aligned} L1是否位于该范围内见上式~。
∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ 1 − α ⋅ 2 L m L + m = 1 − 1 L ⋅ 2 L m L + m = L − m L + m = λ m a x − λ m i n λ m a x + λ m i n \begin{aligned} \frac{||x_k - \alpha \cdot \nabla f(x_k) - x^*||}{||x_k- x^*||} & \leq \sqrt{1 - \alpha \cdot \frac{2\mathcal L m}{\mathcal L + m}} \\ & = \sqrt{1 - \frac{1}{\mathcal L} \cdot \frac{2 \mathcal L m}{\mathcal L + m}} \\ & = \sqrt{\frac{\mathcal L - m}{\mathcal L + m}} = \sqrt{\frac{\lambda_{max} - \lambda_{min}}{\lambda_{max} + \lambda_{min}}} \end{aligned} ∣∣xk−x∗∣∣∣∣xk−α⋅∇f(xk)−x∗∣∣≤1−α⋅L+m2Lm=1−L1⋅L+m2Lm=L+mL−m=λmax+λminλmax−λmin
将根号内分子、分母同时除以 λ m i n \lambda_{min} λmin:
其中λ m a x λ m i n \begin{aligned}\frac{\lambda_{max}}{\lambda_{min}}\end{aligned} λminλmax被称作Hessian Matrix ⇒ ∇ 2 f ( ⋅ ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(\cdot) Hessian Matrix⇒∇2f(⋅)的条件数 ( Condition Number ) (\text{Condition Number}) (Condition Number),记作K [ ∇ 2 f ( ⋅ ) ] \mathcal K[\nabla^2 f(\cdot)] K[∇2f(⋅)]。这里并不关注它的性质,仅从推倒的角度观察K [ ∇ 2 f ( ⋅ ) ] \mathcal K [\nabla^2 f(\cdot)] K[∇2f(⋅)]变化对收敛速度的影响。这里推荐一篇关于条件数的文章,见文章末尾链接。分子、分母同时除以K [ ∇ 2 f ( ⋅ ) ] \mathcal K[\nabla^2 f(\cdot)] K[∇2f(⋅)]。
∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ λ m a x λ m i n − 1 λ max λ m i n + 1 = K [ ∇ 2 f ( ⋅ ) ] − 1 K [ ∇ 2 f ( ⋅ ) ] + 1 = 1 − 1 K [ ∇ 2 f ( ⋅ ) ] 1 + 1 K [ ∇ 2 f ( ⋅ ) ] \begin{aligned}\frac{||x_k - \alpha \cdot \nabla f(x_k) - x^*||}{||x_k- x^*||} & \leq \sqrt{\frac{\frac{\lambda_{max}}{\lambda_{min}} - 1}{\frac{\lambda_{\max}}{\lambda_{min}} + 1}} \\ & = \sqrt{\frac{\mathcal K [\nabla^2 f(\cdot)] - 1}{\mathcal K[\nabla^2 f(\cdot)] + 1}} \\ & = \sqrt{\frac{1 - \frac{1}{\mathcal K [\nabla^2 f(\cdot)]}}{1 + \frac{1}{\mathcal K [\nabla^2 f(\cdot)]}}} \end{aligned} ∣∣xk−x∗∣∣∣∣xk−α⋅∇f(xk)−x∗∣∣≤λminλmax+1λminλmax−1=K[∇2f(⋅)]+1K[∇2f(⋅)]−1=1+K[∇2f(⋅)]11−K[∇2f(⋅)]1
通过观察可以发现:如果 K [ ∇ 2 f ( ⋅ ) ] \mathcal K[\nabla^2 f(\cdot)] K[∇2f(⋅)]充分大,有:
lim K [ ∇ 2 f ( ⋅ ) ] ⇒ ∞ 1 − 1 K [ ∇ 2 f ( ⋅ ) ] 1 + 1 K [ ∇ 2 f ( ⋅ ) ] = 1 − 0 1 + 0 = 1 \mathop{\lim}\limits_{\mathcal K[\nabla^2 f(\cdot)] \Rightarrow \infty}\sqrt{\frac{1 - \frac{1}{\mathcal K [\nabla^2 f(\cdot)]}}{1 + \frac{1}{\mathcal K [\nabla^2 f(\cdot)]}}} = \sqrt{\frac{1 - 0}{1 + 0}} = 1 K[∇2f(⋅)]⇒∞lim1+K[∇2f(⋅)]11−K[∇2f(⋅)]1=1+01−0=1
这意味着: ∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ 1 \begin{aligned}\frac{||x_k - \alpha \cdot \nabla f(x_k) - x^*||}{||x_k- x^*||} \leq 1\end{aligned} ∣∣xk−x∗∣∣∣∣xk−α⋅∇f(xk)−x∗∣∣≤1,而这意味着此时的收敛速度位于退化边缘。
如果上式取等的话,那么收敛速度会从 Q \mathcal Q Q-线性收敛退化至次线性收敛。
因而通常称条件数 K [ ∇ 2 f ( ⋅ ) ] \mathcal K[\nabla^2 f(\cdot)] K[∇2f(⋅)]过大的现象称作病态问题。
这也体现了梯度下降法的弊端:如果函数 f ( ⋅ ) f(\cdot) f(⋅)二阶可微,其对应 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)的条件数过大可能会导致梯度下降法收敛速度的退化。
而条件数的大小依赖 λ m a x λ m i n \begin{aligned}\frac{\lambda_{max}}{\lambda_{min}}\end{aligned} λminλmax,也就是说:它依赖 λ m a x \lambda_{max} λmax与 λ m i n \lambda_{min} λmin的差异性的大小。因而这个条件数仅取决于 f ( ⋅ ) f(\cdot) f(⋅)是否二阶可微这条性质上。而这条性质同样是 f ( ⋅ ) f(\cdot) f(⋅)的自身性质。一旦 f ( ⋅ ) f(\cdot) f(⋅)确定且二阶可微,那么其 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)确定,从而条件数确定。
相关参考:
【优化算法】梯度下降法-强凸函数的收敛性分析(下)
条件数、奇异值与海森矩阵
相关文章:
梯度下降法在强凸函数的收敛性分析)
机器学习笔记之优化算法(十七)梯度下降法在强凸函数的收敛性分析
机器学习笔记之优化算法——梯度下降法在强凸函数的收敛性分析 引言回顾:梯度下降法在强凸函数的收敛性二阶可微——梯度下降法在强凸函数的收敛性推论 引言 上一节介绍并证明了:梯度下降法在强凸函数上的收敛速度满足 Q \mathcal Q Q-线性收敛。 本节将…...
shell脚本中linux命令的特殊用法记录
shell脚本中linux命令的特殊用法记录 1、linux命令特殊参数选项1.1、sed -e1.2、echo -e 2、 shell 扩展2.1、[[ ]]支持用~进行正则匹配 3、特殊命令用法3.1、{} 变量替换 1、linux命令特殊参数选项 1.1、sed -e sed -e以严格模式执行脚本,在sed -e 后面的所有命令…...

Nvidia H100:今年55万张够用吗?
原文标题:Nvidia H100: Are 550,000 GPUs Enough for This Year? 作者:Doug Eadline August 17, 2023 The GPU Squeeze continues to place a premium on Nvidia H100 GPUs. In a recent Financial Times article, Nvidia reports that it expects to…...
)
【Vue2.0源码学习】生命周期篇-初始化阶段(initLifecycle)
文章目录 1. 前言2. initLifecycle函数分析3. 总结 1. 前言 在上篇文章中,我们介绍了生命周期初始化阶段的整体工作流程,以及在该阶段都做了哪些事情。我们知道了,在该阶段会调用一些初始化函数,对Vue实例的属性、数据等进行初始…...
Android开发基础知识总结(三)简单控件(上)
一.文本显示 考虑到结构样式相分离的思想,我们往往在XML中设置文本 <TextViewandroid:layout_width"342dp"android:layout_height"70dp"android:text"房价计算器"android:layout_gravity"center"android:textColor"…...
在Qt窗口中添加右键菜单
在Qt窗口中添加右键菜单 基于鼠标的事件实现流程demo 基于窗口的菜单策略实现Qt::DefaultContextMenuQt::ActionsContextMenuQt::CustomContextMenu信号API 基于鼠标的事件实现 流程 需要使用:事件处理器函数(回调函数) 在当前窗口类中重写鼠标操作相关的的事件处理器函数&a…...

Day8 智慧商城
项目演示 项目收获 创建项目 调整初始化目录 1.删components里的所有文件 2.删views里的所有文件 3.router/index.js 删路由 删规则 import Vue from vue import VueRouter from vue-routerVue.use(VueRouter)const router new VueRouter({routes: [] })export default route…...

LeetCode:Hot100python版本之回溯
回溯算法其实是纯暴力搜索。for循环嵌套是写不出的 组合:没有顺序 排列:有顺序 回溯法可以抽象为树形结构。只有在回溯算法中递归才会有返回值。 46. 全排列 排列是有顺序的。 组合类问题用startindex,排序类问题用used,来标…...
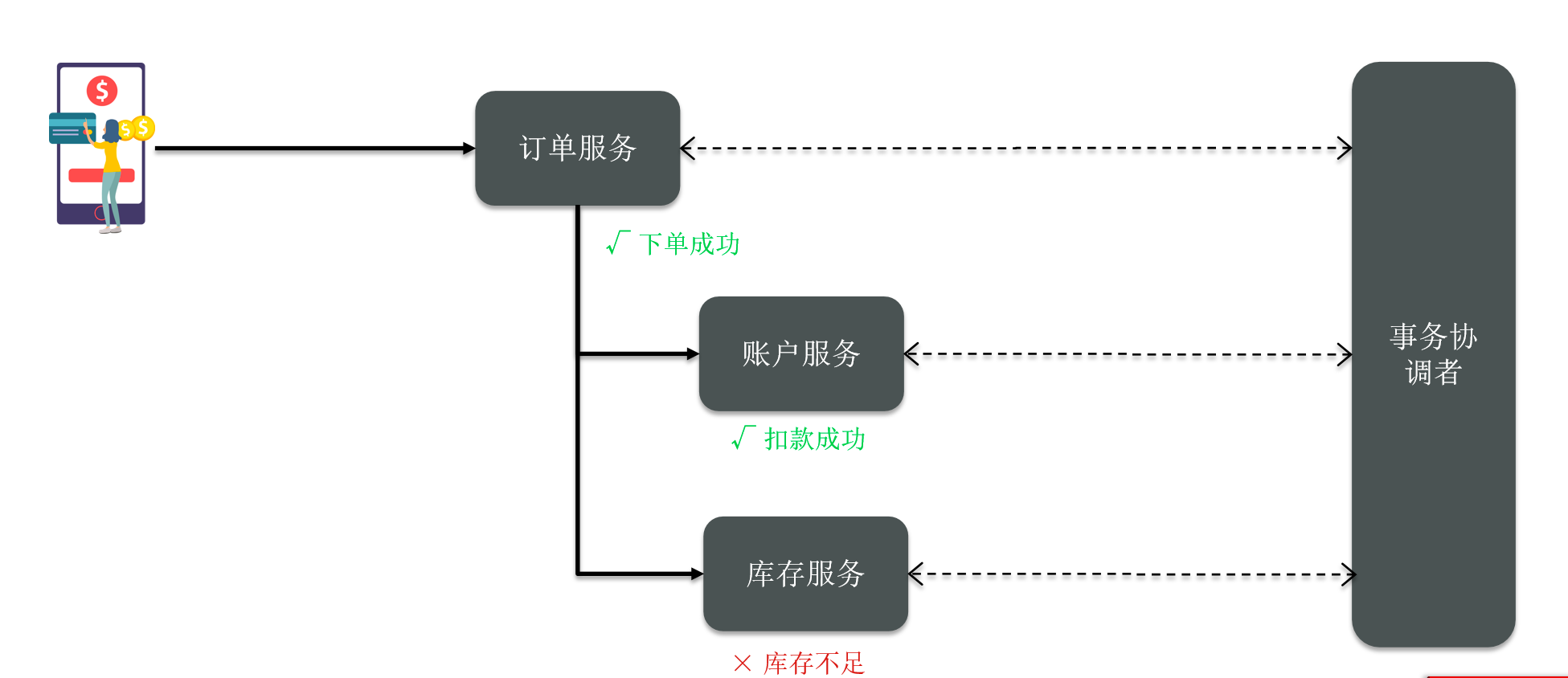
分布式事务理论基础
今天啊,本片博客我们一起来学习一下微服务中的一个重点和难点知识:分布式事务。 我们会基于Seata 这个框架来学习。 1、分布式事务问题 事务,我们应该比较了解,我们知道所有的事务,都必须要满足ACID的原则。也就是 …...

线性代数强化第三章
目录 一,关于A伴随,A逆与初等矩阵 二,分块矩阵 三,矩阵方程 一,关于A伴随,A逆与初等矩阵 如何证明行列式的值不能是0; 此秩为1. 法一: 法二: 不用看是列变换还是行变…...
---之配置)
搭建自己的私有 开源LoRaWAN 网络服务器(The ThingsStack)---之配置
介绍 这是使用 Docker 在您自己的硬件上安装 Things Stack Enterprise 或开源代码以运行您自己的私有 LoRaWAN 网络服务器的指南。 运行 The Things Stack 的方法有多种。 Things Stack 开源和企业发行版旨在在您自己的硬件上运行,本指南也对此进行了介绍。 对于具有高吞吐量的…...
多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测
多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测 目录 多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.SCNGO-CNN-Attention超前24步多变量回归预测算法。 程序平台:无Attention适…...

clickhouse的删除和更新
clickhouse不擅长更新和删除操作,更新操作很重,更新是重新创建一个分区,更新完后,太混之前的 ClickHouse提供了DELETE和UPDATE的能力,这类操作被称为Mutation查询,它可以看作ALTER语句的变种。虽然Mutation…...
微前端 - qiankun
qiankun 是一个基于 single-spa 的微前端实现库,旨在帮助大家能更简单、无痛的构建一个生产可用微前端架构系统。 本文主要记录下如何接入 qiankun 微前端。主应用使用 vue2,子应用使用 vue3、react。 一、主应用 主应用不限技术栈,只需要提…...

前端编辑页面修改后和原始数据比较差异
在软件研发过程中,会遇到很多编辑页面,有时编辑页面和新增页面长的基本上一样,甚至就是一套页面供新增和编辑共用。编辑页面的场景比较多,例如: 场景一、字段比较多,但实际只修改了几个字段,如…...

docker第一次作业
docker第一次作业 1.安装docker服务,配置镜像加速器 yum install -y yum-utils device-mapper-persistent-data lvm2 yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo sed -i sdownload.docker.commirrors.aliy…...

Springboot3.0.0+集成SpringDoc并配置knife4j的UI
环境:JDK17,Springboot3,springdoc2,knife4j 4 Springdoc本身也是集成了Swagger3,而knife4j美化了Swagger3的UI Knife4j官网: 快速开始 | Knife4j Springdoc官网 OpenAPI 3 Library for spring-boot 1.pom配置 由于此knife4j内依赖了S…...
电脑运行缓慢?4个方法,加速电脑运行!
“我电脑才用了没多久哎!怎么突然就变得运行很缓慢了呢?有什么方法可以加速电脑运行速度吗?真的很需要,看看我吧!” 电脑的运行速度快会让用户在使用电脑时感觉愉悦,而电脑运行缓慢可能会影响我们的工作效率…...

3.Docker 搭建 MySQL8.0
1、docker仓库搜索mysql docker search mysql2、docker仓库拉取mysql8.0 docker pull mysql:8.0 备注: docker pull mysql //默认拉取最新版本3、查看本地仓库镜像是否下载成功 docker images mysql:8.04、安装运行mysql8.0容器 docker run -p 3306:3306 --name…...

Mybatis的SqlSource SqlNode BoundSql
学习链接 MyBatis SqlSource解析 【Mybatis】Mybatis源码之SqlSource#getBoundSql获取预编译SQL Mybatis中SqlSource解析流程详解 Mybatis TypeHandler解析 图解 Mybatis的SqlSource&SqlNode - processon DynamicSqlSource public class DynamicSqlSource implement…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
