清风数学建模——拟合算法
拟合算法

文章目录
- 拟合算法
- 概念
- 确定拟合曲线
- 最小二乘法的几何解释
- 求解最小二乘法
- matlab求解最小二乘法
- 如何评价拟合的好坏
- 计算拟合优度的代码
概念
在前面的篇幅中提到可以使用插值算法,通过给定的样本点推算出一定的曲线从而推算出一些想要的值。但存在一些问题。一是若样本点过多,那么多项式的次数过高会造成龙格现象;二是为了避免龙格现象而通过分段的思想求得拟合曲线,但这样会导致曲线函数非常复杂。
针对以上问题,在拟合问题中,不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数(曲线),而该函数尽可能设置得较为简单,使得该曲线在某种准则下与所有的数据点最为接近,即只要保证误差足够小即可,(最小化损失函数),这就是拟合是思想。
确定拟合曲线
给定一组数据[x,y],找出y和x之间的拟合曲线

在matlab上通过画图得出这组数据对应的图像
plot(x,y,'o');
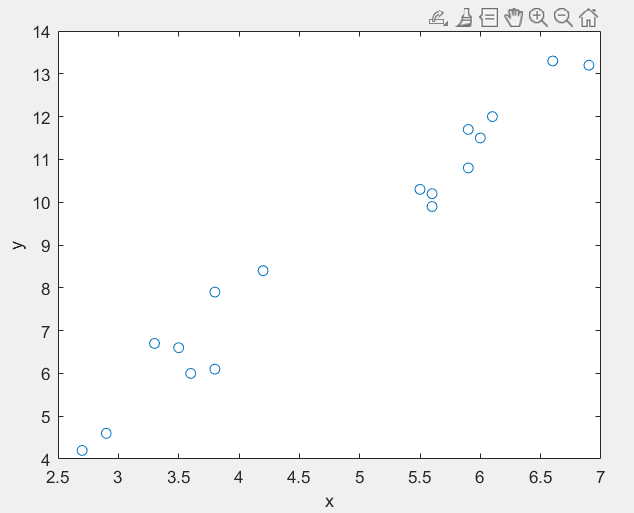
拟合一个曲线去接近样本点,这里我用一个简单的拟合曲线y=kx+b。现在的问题是,k和b取何值时,样本点和拟合曲线最接近。
最小二乘法的几何解释

- 第一种定义有绝对值,后续不容易求导,因此计算较复杂。所以我们往往使用第二种定义,这正是最小二乘法的思想
- 我们也不使用三次方,因为三次方计算样本点到拟合曲线的距离会出现负数,那么该距离就会正负抵消
- 我们也不使用四次方,使用4次方时,若出现某个异常值离曲线较远,那么该拟合曲线受到的影响较大
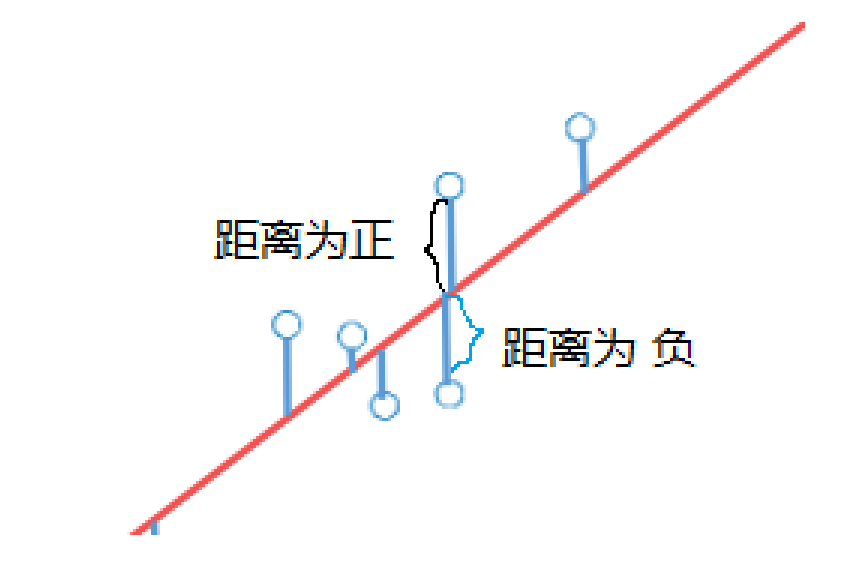
求解最小二乘法

最终落脚到的两个公式:k</sup>和b<sup>推导公式
- 该公式通过对k和b一介求导,然后分离系数所得
matlab求解最小二乘法
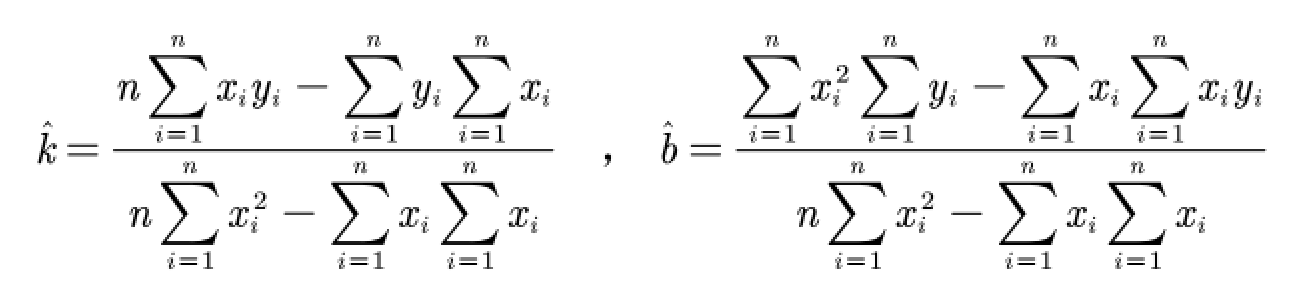
根据公式不难得出代码
plot(x,y,'o');
xlabel("x");
ylabel("y");
n=size(x,1);%% 数据的个数
k=(n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x));
b=(sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x));
hold on;%% 写上这句后续可以继续在之前的图形上画图形
grid on;%% 图形显示网格线
f=@(x) k*x+b; %% f=kx+b是匿名函数,该函数图形不需要另外传参数也能形成图形
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','southeast');
- f函数是匿名函数,该函数图形不需要另外传参数也能形成图形。在matlab中画出图形需要传参。比如正常情况下f函数需要传参x否则不能画出图形,而匿名函数系统会根据需求自己给出一定范围的参数以得画出图形
匿名函数的基本用法
handle = @(arglist) anonymous_function
-
其中handle为调用匿名函数时使用的名字。
-
arglist为匿名函数的输入参数,可以是一个,也可以是多个,用逗号分隔。
-
anonymous_function为匿名函数的表达式。
-
注意输入参数和表达式之间要用空格
- fplot可用于画出匿名一元函数的图形
基本用法
fplot(f,xinterval)
- 将匿名函数f在指定区间xinterval绘图。xinterval = [xmin xmax] 表示定义域的范围
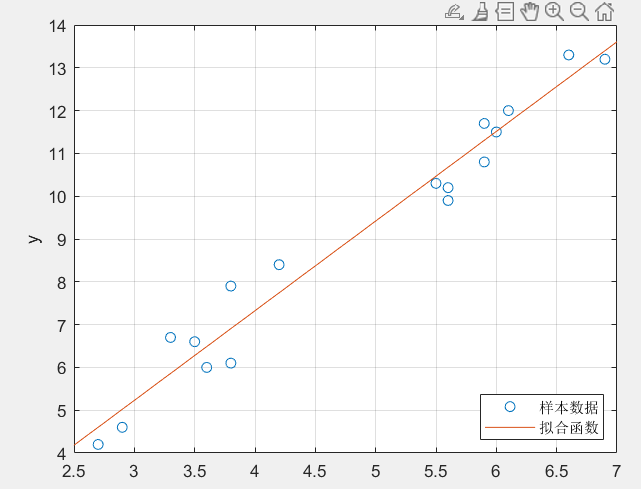
如何评价拟合的好坏

- 根据SST、SSE、SSR可以证明:
- SST=SSE+SSR
- 拟合优度:0<=1-SSE/SST<=1;而SSE误差平方和越小,拟合优度R2越接近1。误差越小说明拟合的越好
- 注意:拟合优度R2只能用于拟合函数是线性函数,若拟合函数是其他函数,直接看误差平方和即可,SSE越小,说明拟合度越好
- 线性函数是指在函数中,参数仅以一次方出现,且不能乘以或除以其他任何的参数,并不能出现参数的复合函数形式。该参数不是指自变量x。比如y=kx+b,该参数指的是区别于自变量x和因变量y以外的参数k和b。

计算拟合优度的代码
plot(x,y,'o');
xlabel("x");
ylabel("y");
n=size(x,1);%% 数据的个数
k=(n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x));
b=(sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x));
hold on;%% 写上这句后续可以继续在之前的图形上画图形
grid on;%% 图形显示网格线
f=@(x) k*x+b; %% f=kx+b是匿名函数,该函数图形不需要另外传参数也能形成图形
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','southeast');
y_hat=k*x+b;
SSR=sum((y_hat-mean(y)).^2); % 回归平方和
SSE=sum((y-y_hat).^2); % 误差平方和
SST=sum((y-mean(y)).^2); % 总体平方和
disp(SST-SSE-SSR);
R_2=SSR/SST; % 拟合优度
disp(R_2);

-
SST-SSE-SSR的结果不为0的原因是在matlab中浮点数做运算一定程度上结果不精准,但结果是5.6843^-14结果是非常小的即非常接近0
[外链图片转存中…(img-WkmLP3WM-1692188156893)] -
SST-SSE-SSR的结果不为0的原因是在matlab中浮点数做运算一定程度上结果不精准,但结果是5.6843^-14结果是非常小的即非常接近0
-
拟合度为0.9635非常接近1了,说明该拟合函数的拟合度较好
相关文章:

清风数学建模——拟合算法
拟合算法 文章目录 拟合算法概念 确定拟合曲线最小二乘法的几何解释求解最小二乘法matlab求解最小二乘法如何评价拟合的好坏计算拟合优度的代码 概念 在前面的篇幅中提到可以使用插值算法,通过给定的样本点推算出一定的曲线从而推算出一些想要的值。但存在一些问题…...

单片机 (一) 让LED灯 亮
一:硬件电路图 二:软件代码 #include "reg52.h"#define LED_PORT P2void main() {LED_PORT 0x01; // 0000 0001 D1 是灭的 } #include "reg52.h" 这个头文件的作用:包含52 系列单片机内部所有的功能寄存器 三&#…...

c++——单例模式
c单例模式 1、概念: 单例模式确保一个类只有一个实例,并提供一个全局访问点以获取该实例。这通常通过让类的构造函数为私有,以防止外部直接实例化,然后提供一个静态方法来获取实例。 2、实现方法: 实现单例模式的主…...
——FileStream、BinaryReader、MemorySream、SreamReader等之间的关系)
C# 流Stream详解(2)——FileStream、BinaryReader、MemorySream、SreamReader等之间的关系
【文件流】 电脑上的文件有很多,文本文件、音频文件、视频文件、图片文件等,这些文件会被持久化存储在磁盘上,其本质都是一堆二进制数据。 FileStream用于读取二进制文件。电脑上的所有文件,不管是文本、音频、视频还是其他任意…...
【JavaSE】详解final关键字
在Java中,final可以用来修饰类、方法和变量。final修饰类,表示该类无法被继承,并且此类的设计已被认为很完美而不需要进行修改或扩展。final修饰类中的方法,表示不可以被重写;也就是把该方法锁定了,以防止继…...

问道管理:机器人概念走势活跃,新时达涨停,拓斯达、丰立智能等大涨
机器人概念17日盘中走势活跃,到发稿,拓斯达大涨18%,昊志机电涨近16%,丰立智能涨超13%,步科股份、优德精细涨超10%,新时达涨停,天玑科技、兆龙互联、中大力德涨逾9%。 消息面上,8月16…...
elementui 修改日期选择器el-date-picker样式
1. 案例: 2. css /* 最外层颜色 */ .el-popper.is-pure {background: url("/assets/imgList/memuBG.png") no-repeat;border: none;background-size:100% 100%}/* 日期 1.背景透明 */ .el-date-picker{background: transparent; }/* 日期 2.标题、左右图…...
自己实现 SpringMVC 底层机制 系列之-实现任务阶段 6-完成控制器方法获取参数-@RequestParam
😀前言 自己实现 SpringMVC 底层机制 系列之-实现任务阶段 6-完成控制器方法获取参数-RequestParam 🏠个人主页:尘觉主页 🧑个人简介:大家好,我是尘觉,希望我的文章可以帮助到大家,…...

数据可视化:图表绘制详解
数据可视化是一种将抽象的数字和数据转化为直观图形的技术,使数据的模式、趋势和关系一目了然。本文将详细介绍如何绘制各种类型的图表,包括柱状图、折线图、饼图、散点图和热力图等。 第一部分:图表类型和选择 1. 柱状图 柱状图是用于比较类…...

【中危】Apache Ivy<2.5.2 存在XXE漏洞 (CVE-2022-46751)
漏洞描述 Apache Ivy 是一个管理基于 ANT 项目依赖关系的开源工具,文档类型定义(DTD)是一种文档类型定义语言,它用于定义XML文档中所包含的元素以及元素之间的关系。 Apache Ivy 2.5.2之前版本中,当解析自身配置、Ivy 文件或 Apache Maven 的 POM 文件…...
C#使用自定义的比较器对版本号(编码)字符串进行排序
给定一些数据,如下所示: “1.10.1.1.1.2”, “1.1”, “2.2”, “1.1.1.1”, “1.1.3.1”, “1.1.1”, “2.10.1.1.1”, “1.1.2.1”, “1.2.1.1”, “2.5.1.1”, “1.10.1.1”, “1.10.2.1”, “1.11.3.1”, “1.11.12.1”, “1.11.11.1”, “1.11.3.1”, “1”, “…...

AI在日常生活中的应用:从语音助手到自动驾驶
文章目录 AI的定义和发展AI在日常生活中的应用1. **智能语音助手**2. **智能家居**3. **智能医疗**4. **自动驾驶** 代码示例:使用Python实现基于机器学习的图片分类AI的未来前景结论 🎉欢迎来到AIGC人工智能专栏~探索AI在日常生活中的应用 ☆* o(≧▽≦…...
Windows10查看图片的分辨率
文章目录 查看方法 查看方法 鼠标悬停在想查看分辨率大小的图片上,稍等那么零点几秒,就会弹出图片的分辨率信息,如图所示:...

Spring事务和事务传播机制(2)
前言🍭 ❤️❤️❤️SSM专栏更新中,各位大佬觉得写得不错,支持一下,感谢了!❤️❤️❤️ Spring Spring MVC MyBatis_冷兮雪的博客-CSDN博客 在Spring框架中,事务管理是一种用于维护数据库操作的一致性和…...
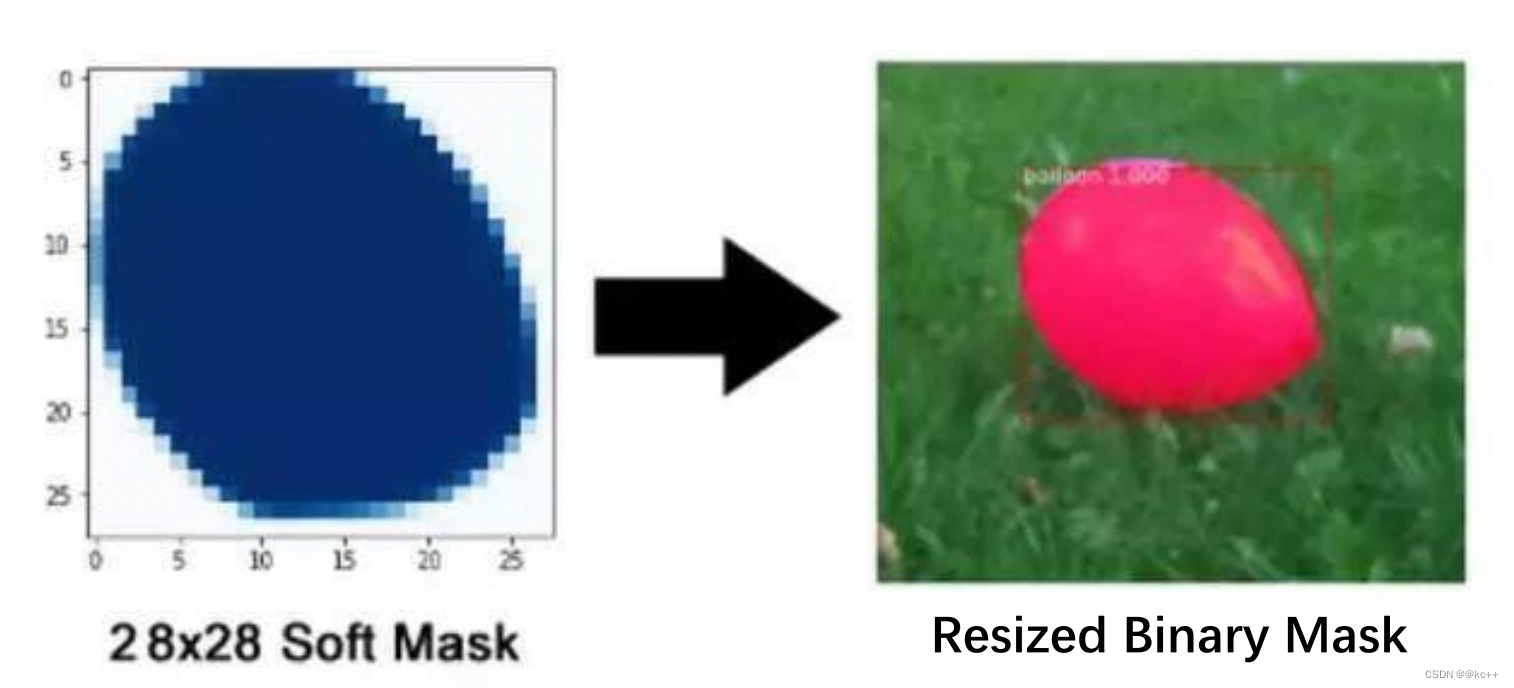
计算机视觉 -- 图像分割
文章目录 1. 图像分割2. FCN2.1 语义分割– FCN (Fully Convolutional Networks)2.2 FCN--deconv2.3 Unpool2.4 拓展–DeconvNet 3. 实例分割3.1 实例分割--Mask R-CNN3.2 Mask R-CNN3.3 Faster R-CNN与 Mask R-CNN3.4 Mask R-CNN:Resnet1013…...

ubuntu18.04复现yolo v8之CUDA与pytorch版本问题以及多CUDA版本安装及切换
最近在复现yolo v8的程序,特记录一下过程 环境:ubuntu18.04ros melodic 小知识:GPU并行计算能力高于CPU—B站UP主说的 Ubuntu可以安装多个版本的CUDA。如果某个程序的Pyorch需要不同版本的CUDA,不必删除之前的CUDA,…...

Redis三种模式——主从复制,哨兵模式,集群
目录 一、主从复制 1.1主从复制的概念 1.2Redis主从复制作用 1.2.1数据冗余 1.2.2故障恢复 1.2.3负载均衡 1.2.4高可用基石 1.3Redis主从复制流程 1.4部署Redis 主从复制 1.4.1.环境部署 1.4.2.所有服务器都先关闭防火墙 1.4.3.所有服务器都安装Redis 1.4.4修改Master主节点R…...

mysql8.0.31新增只读远程普通用户
在 MySQL 8.0.31 中,可以通过以下步骤新增只读远程普通用户: 1、使用 root 用户登录 MySQL 数据库。 mysql -u root -p 2、创建用户: CREATE USER username% IDENTIFIED WITH mysql_native_password BY password ; 其中,username…...

揭开路由协议隐藏的风险
路由协议在互联网和基于其的服务的运行中发挥着至关重要的作用。然而,许多这些协议的开发都没有考虑到安全问题。 例如,边界网关协议 (BGP) 最初并未考虑对等点之间发生攻击的可能性。过去几十年来,BGP 中的起源和路径验证已投入了大量工作。…...
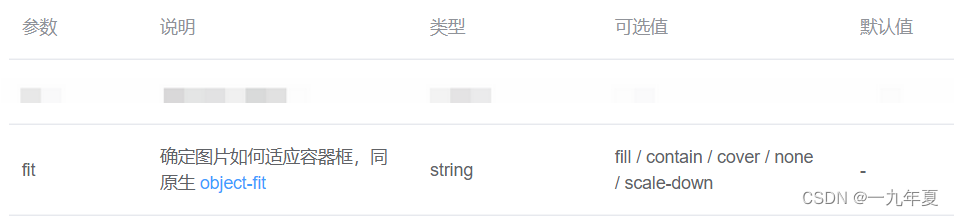
图片因固定宽高被拉伸了?object-fit:一个神奇的属性
一、问题产生的场景 近期在完成项目开发时,测试人员针对漫画长图上传后的展示提出了一个界面优化的点,因为其特点是长,但是我们展示图片的区域是固定的,如果我们按照正常思路将图片的宽高写死,确实占位大小的问题解决了…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
