5.7 汇编语言:汇编高效乘法运算
乘法指令是一种在CPU中实现的基本算术操作,用于计算两个数的乘积。在汇编语言中,乘法指令通常是通过mul(无符号乘法)和imul(有符号乘法)这两个指令实现的。由于乘法指令在执行时所消耗的时钟周期较多,所以编译器在优化代码时通常会尝试将乘法操作转换为更高效的加法、和移位操作。
-
对于较小的数,编译器可能会选择将乘法操作直接转换为加法操作。例如,将表达式
a * b转换为a + a + ... + a(b次相加)的形式。这种方式可以通过循环展开、代码向量化等技术来优化。 -
对于较大的数,编译器可能会使用位移和移位操作来代替乘法。例如,将表达式
a * b转换为a << n + a << m的形式,其中n和m为符合条件的位数。这种方式可以通过位移指令的高效性来加速运算。
当以上方式均无法进行优化时,编译器才会使用mul/imul指令来执行乘法操作。这两条指令可以对无符号数和有符号数进行乘法运算,即便这两条指令会使用更多的时钟周期,但乘法指令的计算效率相对于其他指令DIV来说仍然较低,因此在编写高效代码时,应尽可能地避免使用乘法操作,并结合使用上面提到的技巧进行优化。
7.1 使用IMUL指令完成乘法
要计算乘法在不考虑执行效率的情况下编译器通常会直接使用imul指令完成计算,imul指令在一些情况下可以比其他乘法指令(如mul指令)更快地执行乘法运算,但性能较低的原因主要是由于imul指令通常用于有符号数的乘法运算,并且在执行时需要处理符号位的扩展和溢出问题,这转换成了额外的指令和时钟周期的消耗。如果对于无符号整数或需要使用寄存器的低位或者高位结果的情况,使用imul指令可以提供一定的优势。
计算乘法时应遵循:
- 如果乘数与被乘数都是
8位则把AL做乘数,结果放在AX中 - 如果乘数与被乘数都是
16位将把AX做乘数,结果放在EAX中 - 如果乘数与被乘数都是
32位将把EAX做乘数,结果放在EDX:EAX中
乘法指令计算很简单,只需要累加乘数即可,如下所示则是一个简单的计算三个数相乘的汇编实现;
.datax DWORD ?y DWORD ?z DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],10mov dword ptr ds:[y],24mov dword ptr ds:[z],18; 计算 x * y * zmov eax,dword ptr ds:[x]imul eax,dword ptr ds:[y]imul eax,dword ptr ds:[z]invoke crt_printf,addr szFmt,eaxmain ENDP
END main
7.2 使用LEA指令替换乘法
在实际编程中,我们可以使用LEA指令来替代乘法操作,从而提高代码的执行效率。但读者需要注意,在使用LEA计算乘法时必须要保证乘数是2的次幂,并且乘数的范围必须是2/4/8这三个区间才可使用该指令,我们使用汇编来实现计算eax*8+2其汇编指令如下。
- 假设
eax=5计算eax * 8 + 2的结果,拆分过程如下: - 1.计算
lea ebx,dword ptr ds:[eax * 8 + 2]这就相当于计算ebx = (eax * 8) +2直接可得到结果。
第一个案例比较简单,可直接使用一条lea指令即可完成计算过程,只要保证被乘数是2的次幂即可。
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROC; 针对乘法的lea指令优化mov dword ptr ds:[x],5mov eax,dword ptr ds:[x] ; eax = xxor ebx,ebx ; ebx = 0lea ebx,dword ptr ds:[eax * 8 + 2] ; ebx = eax * 8 + 2invoke crt_printf,addr szFmt,ebxinvoke ExitProcess,0main ENDP
END main
7.3 使用LEA指令拆分计算
如果我们计算的乘法超出了2/4/8次幂范围,则需要对乘法进行拆分,拆分时也应遵循2的次幂原则,拆分后在分开来计算。
- 假设
eax=3计算15 * eax的结果,拆分过程如下: - 1.计算
lea edx,[eax * 4 + eax]这就相当于计算edx = (4 * eax) + eax = 5eax其中的每个edx就相当于5个eax - 2.计算
lea edx,[edx * 2 + edx]这就相当于计算edx = (5 * eax) * 2 + (5 * eax) - 3.计算
(5eax * 2) = 10eax接着计算(5 * eax) = 5eax最后得出10eax + 5eax - 4.经过该过程可得出
eax * 15 = 45最终计算3*15=45得到最终结果.
这个计算过程看似复杂,但如果将其转化为汇编指令那么只需要两条即可实现快速乘法运算。
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROC; 针对乘法的lea指令优化mov dword ptr ds:[x],3; 如果使用lea计算乘法,则乘数必须是2/4/8mov eax,dword ptr ds:[x] ; eax = 3lea edx,dword ptr ds:[eax * 4 + eax] ; edx = 4eax + eax 得出 5eax,也就是说每一个edx就代表5个eaxlea edx,dword ptr ds:[edx * 2 + edx] ; edx = (5eax * 2) + 5eax 最终得出 15eaxinvoke crt_printf,addr szFmt,edx ; edx = eax * 15 计算后得出 45invoke ExitProcess,0main ENDP
END main
7.4 使用LEA指令递减计算
如果计算乘法时乘数非2的次幂,这种情况下需要减去特定的值,例如当我们计算eax * 7时,由于7非二的次幂,我们无法通过lea指令进行计算,但我们可以计算eax * 8计算出的结果减去一个eax同样可以得到正确的值。
- 假设
eax=3计算eax * 7 + 10的结果,拆分过程如下: - 1.计算
lea edx,dword ptr ds:[eax * 8]这就相当于计算edx = (8 * eax) - 2.计算
sub edx,eax这就相当于计算edx = (8 * eax) - eax - 3.计算
add edx,10这就相当于计算edx = ( (8 * eax) - eax ) + 10 - 4.经过如上计算,我们就可以计算出
eax * 7 + 10的最终结果
这个计算过程看似复杂,但其实在汇编层面并不难构建,如下分别实现计算两个表达式求值过程。
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROC; 针对乘法的lea指令优化mov dword ptr ds:[x],3; 如果计算乘法时乘数非2的次幂,则此时需要减; 计算 edx = eax * 7 + 10mov eax,dword ptr ds:[x] ; eax = 3 => 计算 eax * 7 + 10lea edx,dword ptr ds:[eax * 8] ; edx = eax * 8sub edx,eax ; edx = edx - eaxadd edx,10 ; edx = edx + 10invoke crt_printf,addr szFmt,edx ; edx = eax * 7 + 10; 计算 edx = eax * 3 - 7mov eax,dword ptr ds:[x] ; eax = 3 => 计算 eax * 3 - 7lea edx,dword ptr ds:[eax * 2] ; edx = eax * 2add edx,eax ; edx = edx + eaxsub edx,7 ; edx = edx - 7invoke crt_printf,addr szFmt,edx ; edx = eax * 3 - 7invoke ExitProcess,0main ENDP
END main
7.5 使用SHL计算无符号乘法
通过使用逻辑左移同样可以实现2的次幂的高速乘法运算,但逻辑左移只能用于计算无符号乘法,且只能计算被乘数是2的次方的算式。
-
计算时我们需要参考次方表,这里我列举出几个常用的次方数值:
-
次方表: 1=>2 2=>4 3=>8 4=>16 5=>32 6=>64 7=>128
-
次方表: 8=>256 9=>512 10=>1024 11=>2048 12=>4096 13=>8192 14=>16384
-
假设
eax=3计算eax * 8 + 10的结果,拆分过程如下: -
1.计算
shl eax,3这就相当于计算eax = eax * 2 ^(次方) 3其公式相当于计算eax = eax * 8 -
2.计算
add eax,10这就相当于计算eax = (eax * 8) + 10 -
3.最终即可得到计算结果也就是
3*8+10得到34
通过使用逻辑左移,我们可以实现快速无符号乘法运算,如下代码是效率最高的一种。
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],3; 计算 eax = eax * 2 ^ 1 相当于计算 eax * 2mov eax,dword ptr ds:[x]shl eax,1invoke crt_printf,addr szFmt,eax; 计算 eax = eax * 2 ^ 2 相当于计算 eax * 4mov eax,dword ptr ds:[x]shl eax,2invoke crt_printf,addr szFmt,eax; 计算 eax = eax * 2 ^ 3 相当于计算 eax * 8mov eax,dword ptr ds:[x]shl eax,3add eax,10invoke crt_printf,addr szFmt,eaxinvoke ExitProcess,0main ENDP
END main
7.6 使用SAL计算有符号乘法
通过使用算数左移同样可以实现2的次幂的高速乘法运算,与逻辑左移不同,算术左移只能计算有符号乘法,且只能计算被乘数是2的次方的算式。
-
计算时我们需要参考次方表,这里我列举出几个常用的次方数值:
-
次方表: 1=>2 2=>4 3=>8 4=>16 5=>32 6=>64 7=>128
-
次方表: 8=>256 9=>512 10=>1024 11=>2048 12=>4096 13=>8192 14=>16384
-
假设
eax=-5,ebx=3计算(eax * 8) + (ebx * 4)的结果,拆分过程如下: -
1.计算
sal eax,3这就相当于计算eax = (eax * 2 ^ 3 )其公式相当于计算eax = eax * 8结果是一个有符号数 -
2.计算
shl ebx,2这就相当于计算ebx = (ebx * 2 ^2)其公式相当于计算ebx = ebx * 4结果是一个无符号数 -
3.最终将有符号与无符号数通过
add eax,ebx相加,即可得到(eax * 8) + (ebx * 4)的最终结果-28
如下是通过算数左移,实现2的次幂的高速乘法运算,我们可以将算数运算与逻辑运算相加通过此方式提高运算效率。
.datax DWORD ?y DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],-5mov dword ptr ds:[y],3; 计算 eax = eax * 2 ^ 1 相当于计算 eax * 2mov eax,dword ptr ds:[x]sal eax,1invoke crt_printf,addr szFmt,eax; 计算 eax = eax * 2 ^ 2 相当于计算 eax * 4mov eax,dword ptr ds:[x]sal eax,2invoke crt_printf,addr szFmt,eax; 计算 eax = (eax * 2 ^ 3 ) + (ebx * 2 ^2) 相当于计算 (eax * 8) + (ebx * 4)mov eax,dword ptr ds:[x]mov ebx,dword ptr ds:[y]sal eax,3 ; eax * 8 (有符号乘法)shl ebx,2 ; ebx * 4 (无符号乘法)add eax,ebx ; eax + ebxinvoke crt_printf,addr szFmt,eaxinvoke ExitProcess,0main ENDP
END main
乘法优化的知识点基本就这些,除了两个未知变量的相乘无法优化外,其他形式的乘法运算均可以进行优化,如果表达式中存在一个常量值,那编译器则会匹配各种优化策略,最后对不符合优化策略的运算进行调整,如果真的无法优化,则会使用原始乘法指令计算。
本文作者: 王瑞
本文链接: https://www.lyshark.com/post/ade8241c.html
版权声明: 本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
相关文章:

5.7 汇编语言:汇编高效乘法运算
乘法指令是一种在CPU中实现的基本算术操作,用于计算两个数的乘积。在汇编语言中,乘法指令通常是通过mul(无符号乘法)和imul(有符号乘法)这两个指令实现的。由于乘法指令在执行时所消耗的时钟周期较多&#…...

Graphql中的N+1问题
开篇 原文出处 Graphql 是一种 API 查询语言和运行时环境,可以帮助开发人员快速构建可伸缩的 API。然而,尽管 Graphql 可以提供一些优秀的查询性能和数据获取的能力,但是在使用 Graphql 的过程中,开发人员也会遇到一些常见问题&…...

mysql、oracle、sqlserver常见方法区分
整理了包括字符串与日期互转、字符串与数字互转、多行合并为一行、拼接字段等一些常用的函数,当然有些功能实现的方法不止一种,这里列举了部分常用的,后续会持续补充。 MySQLOracleSQL Server字符串转数字 CAST(123 as SIGNED) 或 CONVERT(12…...

AcWing 4382. 快速打字
原题链接:AcWing 4382. 快速打字 关键词:双指针、判断子序列 芭芭拉是一个速度打字员。 为了检查她的打字速度,她进行了一个速度测试。 测试内容是给定她一个字符串 I,她需要将字符串正确打出。 但是,芭芭拉作为一…...
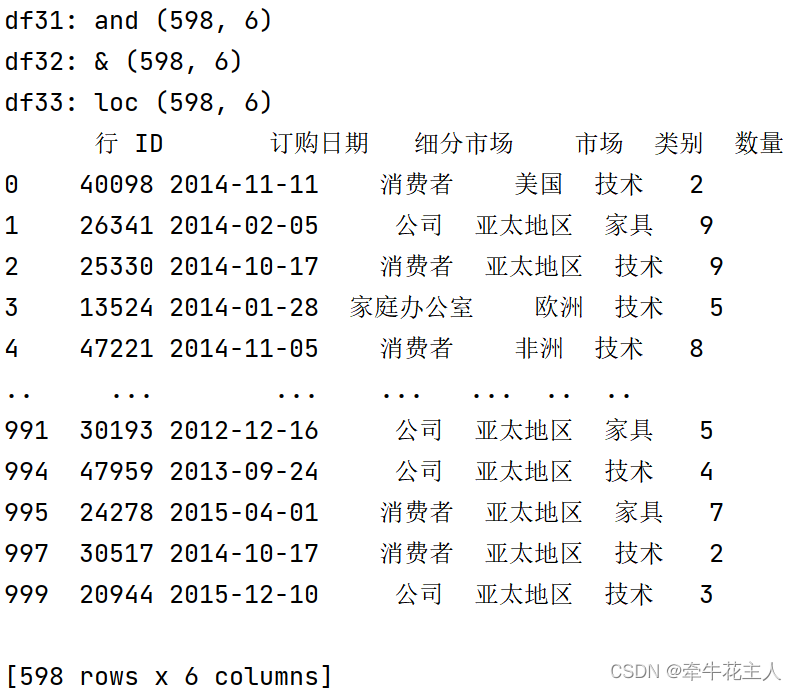
DataFrame.query()--Pandas
1. 函数功能 Pandas 中的一个函数,用于在 DataFrame 中执行查询操作。这个方法会返回一个新的 DataFrame,其中包含符合查询条件的数据行。请注意,query 方法只能用于筛选行,而不能用于筛选列。 2. 函数语法 DataFrame.query(ex…...

【C语言】美元名字和面额对应问题
题目 美元硬币从小到大分为1美分(penny)5美分(nickel)10美分(dime)25美分(quarter)和50美分(half-dollar),写一个程序实现当给出一个数字面额可以…...
)
uniapp隐藏底部导航栏(非自定义底部导航栏)
uniapp隐藏底部导航栏 看什么看,要多看uni官方文档,里面啥都有 看什么看,要多看uni官方文档,里面啥都有 uniapp官方网址:uni设置TabBar // 展示 uni.showTabBar({animation:true,success() {console.debug(隐藏成功)…...

CSS background 背景
background属性为元素添加背景效果。 它是以下属性的简写,按顺序为: background-colorbackground-imagebackground-repeatbackground-attachmentbackground-position 以下所有示例中的花花.jpg图片的大小是4848。 1 background-color background-col…...
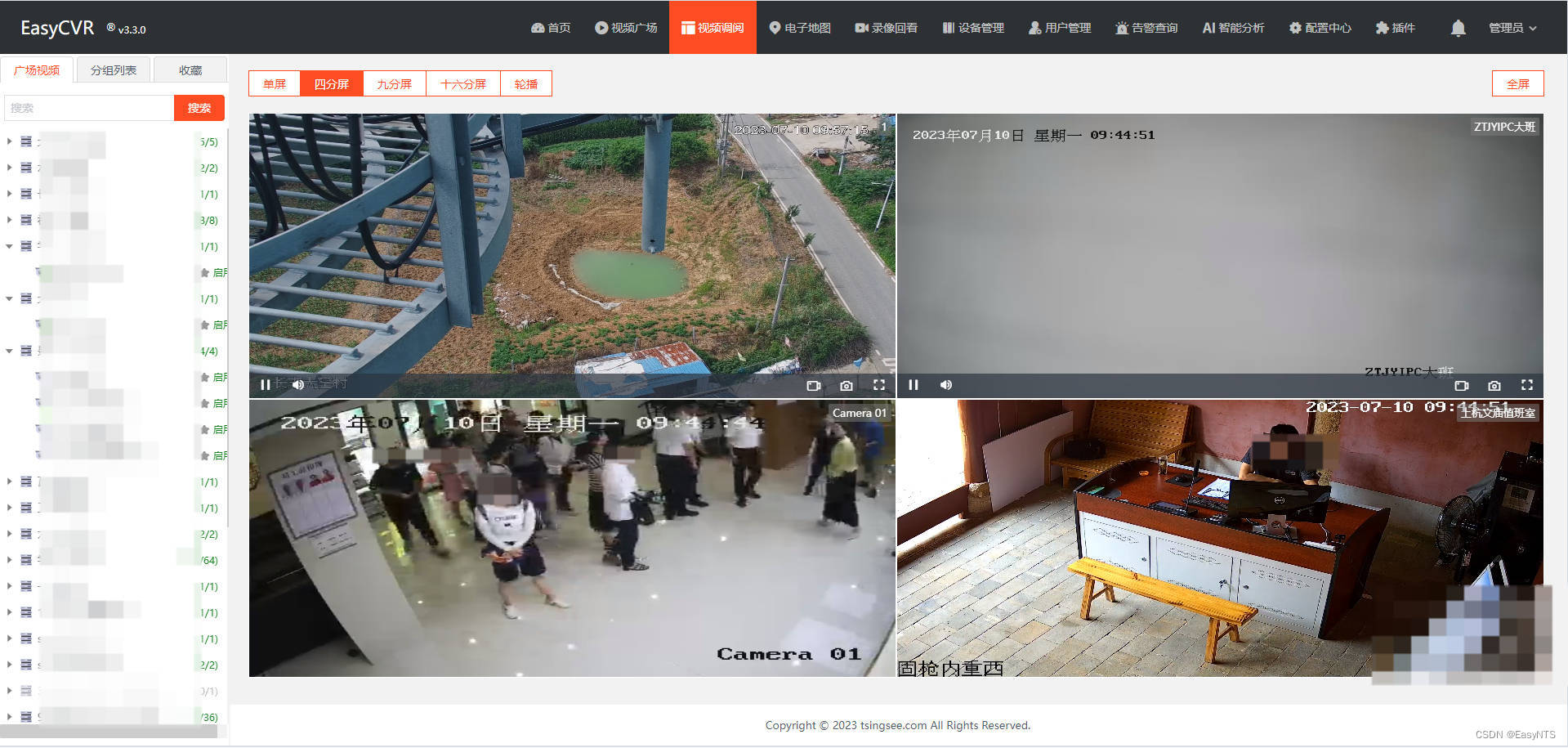
安防监控视频平台EasyCVR视频汇聚平台和税务可视化综合管理应用方案
一、方案概述 为了确保税务执法的规范性和高效性,国家税务总局要求全面推行税务系统的行政执法公示制度、执法全过程记录制度和重大执法决定法制审核制度。为此,需要全面推行执法全过程记录制度,并推进信息化建设,实现执法全过程的…...

深度学习实战50-构建ChatOCR项目:基于大语言模型的OCR识别问答系统实战
大家好,我是微学AI,今天给大家介绍一下深度学习实战50-构建ChatOCR项目:基于大语言模型的OCR识别问答系统实战,该项目是一个基于深度学习和大语言模型的OCR识别问答系统的实战项目。该项目旨在利用深度学习技术和先进的大语言模型,构建一个能够识别图像中文本,并能够回答与…...
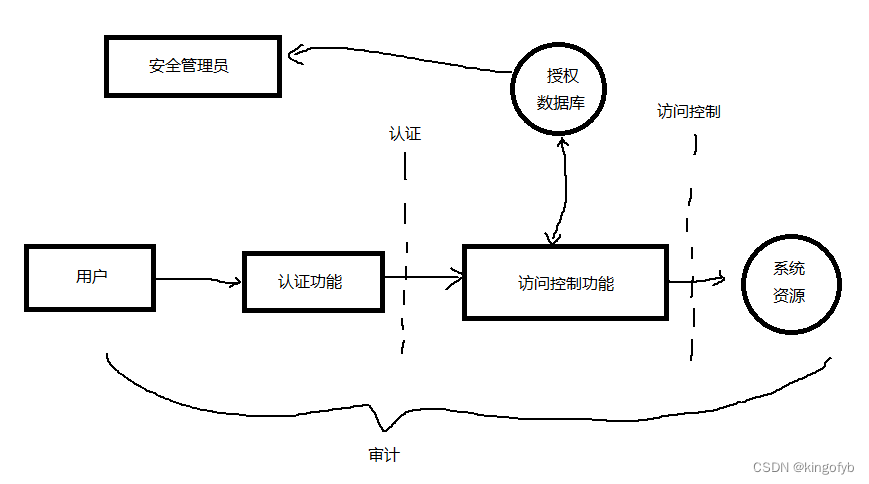
计算机安全学习笔记(I):访问控制安全原理
访问控制原理 从广义上来讲,所有的计算机安全都与访问控制有关。 RFC 4949: Internet Security Glossary, Version 2 (rfc-editor.org) RFC 4949 定义的计算机安全:用来实现和保证计算机系统的安全服务的措施,特别是保证访问控制服务的措施…...
Linux 虚拟机安装 hadoop
目录 1 hadoop下载 2 解压hadoop 3 为 hadoop 文件夹改名 4 给 hadoop 文件夹赋权 5 修改环境变量 6 刷新环境变量 7 在hadoop313目录下创建文件夹data 8 检查文件 9 编辑 ./core-site.xml文件 10 编辑./hadoop-env.sh文件 11 编辑./hdfs-site.xml文件 12 编辑./mapr…...

FxFactory 8 Pro Mac 苹果电脑版 fcpx/ae/motion视觉特效软件包
FxFactory pro for mac是应用在Mac上的fcpx/ae/pr视觉特效插件包,包含了成百上千的视觉效果,打包了很多插件,如调色插件,转场插件,视觉插件,特效插件,文字插件,音频插件,…...

解决问题:如何在 Git 中查看提交历史
可以使用以下命令查看 Git 中的提交历史: git log这将显示当前分支上的所有提交历史。每个提交的输出包括提交哈希(SHA-1 值)、作者、日期和提交注释。 您也可以添加一些选项,以获取更详细的提交历史: --oneline 显示…...
不同规模的测试团队分别适合哪些测试用例管理工具?测试用例管理工具选型指南
随着软件系统规模的持续增大,业务复杂度的持续增加,软件测试的复杂度也随之越来越大。软件测试工作的复杂性主要体现在测试用例的编写、维护、执行和管理方面。而创建易于阅读、维护和管理的测试用例能够显著减轻测试工作的复杂性。 本篇文章将较为系统的…...

服务器遭受攻击,CPU升高,流量升高,你一般如何处理
服务器遭受攻击,CPU升高,流量升高,你一般如何处理? 在什么情况下服务器遭受攻击,会导致CPU升高,流量升高 1.DDoS(分布式拒绝服务攻击):这是一种常见的网络攻击方式&…...

GPT生产实践之定制化翻译
GPT生产实践之定制化翻译 GPT除了能用来聊天以外,其实功能非常强大,但是我们如何把它运用到生产实践中去,为公司带来价值呢?下面一个使用案例–使用gpt做专业领域定制化翻译 思路: 定制化:有些公司词条的…...

SpringMVC入门笔记
一、SpringMVC简介 1. 什么是MVC MVC是一种软件架构的思想,将软件按照模型、视图、控制器来划分 M:Model,模型层,指工程中的JavaBean,作用是处理数据 JavaBean分为两类: 一类称为实体类Bean࿱…...

如何构建多域名HTTPS代理服务器转发
在当今互联网时代,安全可靠的网络访问是至关重要的。本文将介绍如何使用SNI Routing技术来构建多域名HTTPS代理服务器转发,轻松实现多域名的安全访问和数据传输。 SNI代表"Server Name Indication",是TLS协议的扩展,用于…...

【Java 高阶】一文精通 Spring MVC - 数据验证(七)
👉博主介绍: 博主从事应用安全和大数据领域,有8年研发经验,5年面试官经验,Java技术专家,WEB架构师,阿里云专家博主,华为云云享专家,51CTO 专家博主 ⛪️ 个人社区&#x…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
