SimpleCG绘图函数(9)--绘制各种线条
一、所有线段函数概述
可填充图形绘制函数都介绍完了,还有一些特殊线条的绘制将在本篇进行讲解。所有特殊线条函数如下所示,其中还有一个区域填充函数floodfill比较特殊,是配合线条函数使用的:
//绘制一系列折线段
//折线段以一组POINT表示的点坐标数组ptPoints为端点,nNum表示数组中的点数量
void polyline( const POINT *ptPoints, int nNum );//绘制一系列贝塞尔曲线
//数组中开始四个点表示贝塞尔曲线起点,控制点1,控制点2,终点
//其中终点将作为下一段塞尔曲线起点,然后是第二段控制点1,控制点2,终点,循环下去
//所以nNum最少有四个点,总共有3*n+1个点
void polybezier( const POINT *ptPoints, int nNum );//绘制一条曲线,nLength指定拉伸曲度
//绘制一条起点(nStartX, nStartY),到终点(nEndX, nEndY)的曲线,nLength越大曲线越弯曲
void curveline( int nStartX, int nStartY, int nEndX, int nEndY, int nLength );//绘制一系列曲线
//一系列曲线以一组POINT表示的点坐标数组ptPoints为端点,nNum表示数组中的点数量以及曲度pLength的元素数量,pLength的数量为nNum-1。
void polycurvelinevar( const POINT *ptPoints, int *pLength, int nNum );//画椭圆弧
//椭圆弧所在椭圆的外切矩形左上角坐标(left, top),右下角坐标(right, bottom),起始角度stangle,终止角度endangle,角度采用弧度表示,也就是单位圆的弧长度
void arc( int left, int top, int right, int bottom, double stangle, double endangle );//绘制一条波浪线
//绘制一条起点(nStartX, nStartY),到(nEndX, nEndY)波浪线,nLength指定拉伸曲度,nNumLine指定波浪数
void wavyline( int nStartX, int nStartY, int nEndX, int nEndY, int nLength, int nNumLine );//填充区域
//以点(nStartX, nStartY)为起点,开始填充区域,nFillType=enumFFT_BORDER时,填充nColor边线围成的区域。
//当nFillType=enumFFT_SURFACE时,填充nColor指定的一块颜色
void floodfill( int nStartX, int nStartY, COLORREF nColor, int nFillType );由于线条类型比较多,我们分别进行一一展示。
二、各个线段函数演示
1、首先看polyline
跟多边形绘制差不多,参数一致,不同的是polyline不对图形进行填充,只是绘制系列点连接的线段。看如下代码对比:
setfillcolor(RGB(220,240,255));POINT pt[]={{20,20},{300,20},{300,150},{20,150}};
fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));POINT pt1[]={{20,220},{300,220},{300,350},{20,350}};
polyline(pt1,sizeof(pt1)/sizeof(pt1[0]));运行效果如图:
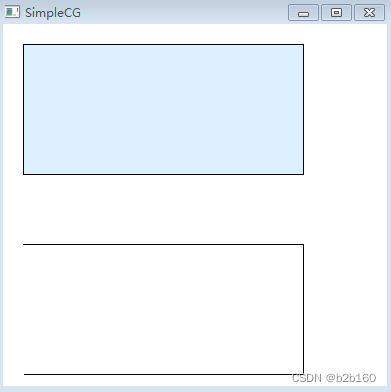
polyline只是单纯把数组中的点连接起来,并不会自动封闭图形。
2、然后是绘制系列贝塞尔曲线的函数polybezier
这是一个非常有用的函数,几乎可以拟合任何曲线,所以对于勾画图形非常重要。其中TrueType字体就是使用了贝塞尔曲线进行拟合,文字的笔画何其复杂,可想而知该函数的强大。当然掌握它也有一定难度。
先看看简单的只有两个端点,两个控制点的贝塞尔曲线演示
POINT pt[]={{20,100},{120,0},{200,200},{300,100}};
polybezier(pt,sizeof(pt)/sizeof(pt[0]));点(20,100)到点(300,100)的曲线,控制点分别在(120,0)和(200,200),两端点之间,而且一上一下,曲线如图所示

曲线如同橡皮筋,被拉向两个端点。
所以只要精确控制端点和控制点,就能绘制任意曲线。下面我们尝试利用它来绘制心形。
POINT pt[]={{20,100},{20,20},{150,20},{150,100},//左上半圆{150,20},{280,20},{280,100},//右上半圆{280,200},{180,200},{150,300},//右下心{120,200},{20,200},{20,100}};//左下心polybezier(pt,sizeof(pt)/sizeof(pt[0]));如图所示
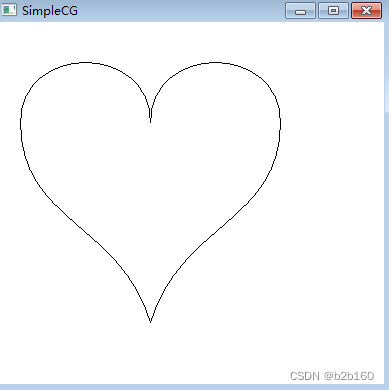
可以看到通过控制点的“拉扯”,很简单就能绘制出优美的符合预期的线条。不过绘制出的线条如果需要填充颜色则需要后面介绍的floodfill函数。
3、下面再看看简单曲线curveline的绘制
贝塞尔曲线需要确定两个控制点,有时一些简单曲线并不需要那么高的自由度,则可以选择curveline来绘制。它可以简单的定义两个端点及一个弯曲程度的参数就绘制出一个弯曲曲线,有时也是比较方便。例如如下代码
curveline(20,100,300,100, 40);就绘制出以下曲线

其中前面四个参数(20,100,300,100)定义了起点和终点,最后一个参数 int nLength,,在此处是40定义了弯曲程度,越大拉伸越厉害,当为正数时表示往终点方向的右侧拉伸,负数则往左拉伸。
4、用多个点绘制一条曲线polycurvelinevar。
上面的函数通过两个点绘制一条简单曲线,而polycurvelinevar则可以同时传入多个点,并以该系列点首尾连接,构成一条复杂的曲线,一系列曲线以一组POINT表示的点坐标数组ptPoints为端点,nNum表示数组中的点数量以及曲度pLength的元素数量,其中pLength的数量为nNum-1。
例如如下代码,用曲线模拟一个近似圆
POINT pt[]={{100,100},{200,100},{200,200},{100,200},{100,100}};//5个点围成一个正方形
int nLength[] = { -30,-30,-30,-30};//每条边往左边拉伸
polycurvelinevar(pt, nLength, sizeof(pt)/sizeof(pt[0]));运行如图所示

可以看出此函数比贝塞尔曲线更简单操控,只是自由度没那么高,要达到理想状态,需要定义更多的点。
5、再来看看椭圆弧绘制函数arc
函数如下
void arc( int left, int top, int right, int bottom, double stangle, double endangle );
参数说明请参考前面的代码,此函数与polyline类似,它的参数与形状函数扇形是一致的,只不过arc同样也只绘制线段。可通过下面的代码看看它们的区别:
setfillcolor(RGB(220,240,255));
fillpie( 20, 20, 300, 150, 0, -C_PI/3);arc( 20, 220, 300, 350, 0, -C_PI/3);绘制效果如图:

这个只绘制圆弧线段在一些情况下作用很大,例如前面绘制的奥运五环,就可以使用这个函数绘制圆圈的环环相扣效果。
6、绘制一条波浪线wavyline
void wavyline( int nStartX, int nStartY, int nEndX, int nEndY, int nLength, int nNumLine );
绘制一条起点(nStartX, nStartY),到(nEndX, nEndY)波浪线,nLength指定拉伸曲度,nNumLine指定波浪数。直接看如下演示代码:
wavyline( 20, 100, 320, 100, 6, 10 );
wavyline( 20, 100+100, 320, 100+100, 6, 20 );两个函数分别用不同的波浪数,同样的曲度,绘制了同样的长度两条波浪线,通过对比可以很容易掌握波浪线的绘制方法。
7、区域填充函数floodfill
void floodfill( int nStartX, int nStartY, COLORREF nColor, int nFillType );
需要注意的是有两种填充模式,分别如下:
nFillType=enumFFT_BORDER时,填充nColor边线围成的区域。
nFillType=enumFFT_SURFACE时,填充nColor指定的一块颜色。
可以通过如下代码演示他们的用法。我们先内外绘制大小两个正方形围成的图形。外围正方形我们用波浪线来绘制。
//以下四条波浪线围成一个大正方形wavyline( 20, 20, 320, 20, 6, 10 );wavyline( 320, 20, 320, 320, 6, 10 );wavyline( 320, 320, 20, 320, 6, 10 );wavyline( 20, 320, 20, 20, 6, 10 );//绘制一个红色正方形setlinecolor(RGB(255,0,0));rectangle( 120,120,220,220);然后分别用两种模式在同一个点进行填充。
setfillcolor(RGB(220,240,255));
floodfill(25, 25, RGB(0,0,0), enumFFT_BORDER );setfillcolor(RGB(220,240,255));
floodfill(25, 25, RGB(255,255,255), enumFFT_SURFACE );原始图形和填充效果如下所示:
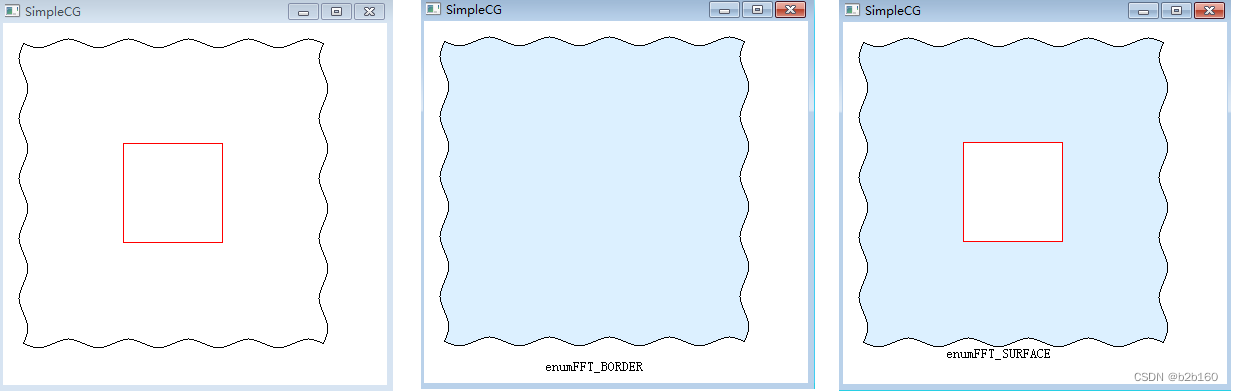
我们看到enumFFT_BORDER模式一直填满到遇到黑色边,所以整个大正方形都填满了。而enumFFT_SURFACE模式则只填充指定点周围白色区域,也就是中间的框。
三、总结及综合演示
以上将所有线段函数详细介绍完了,另外还介绍了一个与线段函数配合使用的floodfill函数。通过以上函数几乎可以模拟所有的矢量图形,前提是只要你能熟练掌握它们。与前面几篇介绍的基础图形绘制相比,本篇所述函数可以绘制生活中各种奇异形状,相比规则图形,也许奇异线条构成的图形更加常见,所以本篇内容在绘图中更加实用。下面就以一个哆啦A梦的绘制演示以上函数的运用。
代码如下:
// Curveline.cpp : 定义控制台应用程序的入口点。
//#include "../import/include/CGBoard.h"
#include "math.h"
#ifdef _DEBUG
#pragma comment(lib,"../import/lib/SimpleCG_MDd.lib")
#else
#pragma comment(lib,"../import/lib/SimpleCG_MD.lib")
#endif#define ADDCOLOR(x,y) ((x+y)>255?255:(x+y))
#define SUBCOLOR(x,y) ((x-y)<0?0:(x-y))int g_nWidth = 500; //画面宽度
int g_nHeight= 800; //画面高度void DrawDora( int nX, int nY )
{setlinewidth( 4 );//竹蜻蜓{POINT pt[]={ { 300, 35},{ 200, 20 },{ 190, 45},{ 290, 55},{ 300, 35}};int nLength[] = { 16, 12, 16, 12 };polycurvelinevar(pt, nLength, sizeof(pt)/sizeof(pt[0]));}curveline(235,30,204,35,4);curveline(242,37,225,38,2);curveline(250,47,266,46,2);curveline(245,55,286,50,4);setfillcolor(RGB(244,225,122));fillpie( 240, 40, 250, 140, 0, -C_PI );fillpie( 225, 90, 265, 127, 0, -C_PI );//头{POINT pt[]={ {235,107}, {264,107}, {325,109}, {367,156}, {409,203}, {398,314}, {376,349}, {354,384}, {350,387}, {340,398}, {330,409}, {161,414}, {125,385}, {89,356}, {57,314}, {66,239}, {75,164}, {151,107}, {237,107} };polybezier(pt, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(1,144,214));floodfill(235,117,0,enumFFT_BORDER);}//脸{POINT pt[]={{237,190}, {266,190}, {321,193}, {348,237}, {375,281}, {362,352}, {343,380}, {324,408}, {232,408}, {214,408}, {196,408}, {160,413}, {124,384}, {88,355}, {68,294}, {79,241}, {90,188}, {176,188}, {237,190} };polybezier(pt, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(255,255,255));floodfill(237,200,0,enumFFT_BORDER);}//嘴{POINT pt[]={{111,268}, {81,246}, {83,264}, {86,275}, {88,300}, {155,281}, {189,276}, {223,271}, {320,266}, {323,282}, {326,298}, {264,384}, {207,385}, {150,386}, {109,293}, {109,290} };polybezier(pt, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(232,47,37));floodfill(189,285,0,enumFFT_BORDER);}{POINT pt[]={{306,314}, {278,293}, {192,310}, {162,365}};int nLength[] = { 5, 12, 8 };polycurvelinevar(pt, nLength, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(232,65,28));floodfill(170,350,0,enumFFT_BORDER);}//眼睛setfillcolor(RGB(254,254,254));fillellipse(130,130,200,220);fillellipse(200,130,270,220);setfillcolor(0);fillellipse(160,187,170,205);fillellipse(230,190,240,205);//鼻子setfillcolor(RGB(239,40,35));fillcircle(186,230,18);setfillcolor(RGB(254,254,254));solidcircle(190,224,6);//胡子line(100,220,150,237);line(90,240,148,250);line(91,262,147,263);line(186,247,186,276);line(300,214,244,231);line(308,236,250,244);line(309,260,250,260);//脚{POINT pt[]={{315,568}, {340,564}, {325,563}, {348,564}, {363,571}, {347,639}, {299,639}, {251,639}, {249,603}, {244,575}};polybezier(pt, sizeof(pt)/sizeof(pt[0]));}{POINT pt[]={{427,472}, {455,468}, {464,502}, {472,519}, {480,536}, {483,598}, {439,606}, {395,614}, {387,591}, {377,570}};polybezier(pt, sizeof(pt)/sizeof(pt[0]));}//身体{POINT pt[]={{336,406}, {397,319}, {396,313}, {429,323}, {462,333}, {407,425}, {400,440}, {427,451}, {450,518}, {418,551}, {386,584}, {357,558}, {349,567}, {340,581}, {342,586}, {296,591}, {250,596}, {154,522}, {148,475}, {121,466}, {33,420}, {52,382}, {71,344}, {148,399}, {173,412}, {198,425}, {319,406}, {335,405}};polybezier(pt, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(1,144,214));floodfill(336,416,0,enumFFT_BORDER);}{POINT pt[]={{171,417}, {231,409}, {305,415}, {331,432}, {357,449}, {387,527}, {315,555}, {243,583}, {164,533}, {147,468}, {140,448},{151,427},{171,417}};polybezier(pt, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(254,254,254));floodfill(181,427,0,enumFFT_BORDER);}{POINT pt[]={{174,481}, {209,484}, {242,499}, {309,473}, {331,487}, {310,548}, {260,545}, {212,542}, {184,529}, {174,481}};polybezier(pt, sizeof(pt)/sizeof(pt[0]));}//铃铛{POINT pt[]={{132,392}, {224,408}, {352,382}, {342,403}, {222,426}, {132,408}, {132,392}};setfillcolor(RGB(232,47,37));fillpolygon(pt, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(248,216,24));fillcircle(225,436,25);setfillcolor(0);solidcircle(225,446,7);line(225,446,225,460);curveline(205, 423,243,423,-4);curveline(201, 430,247,430,-4);}//手setfillcolor(RGB(254,254,254));fillcircle(50,372,30);fillcircle(434,318,30);//尾巴{POINT pt[]={{403,432}, {430,425}, {430,450}, {420,463}};polybezier(pt, sizeof(pt)/sizeof(pt[0]));setfillcolor(RGB(232,47,37));floodfill(413,442,0,enumFFT_BORDER);}}
void DrawProcess()
{DrawDora(20,20);
}
int _tmain(int argc, _TCHAR* argv[])
{//初始化if( !ShowingBoard(g_nWidth,g_nHeight, DrawProcess))return 1;//关闭图库CloseBoard();return 0;
}运行效果如下:

可以看到此例子运用大量曲线绘制方法勾绘线条,用floodfill进行色彩填充.充分展示了线条绘制函数的使用方法。通过对这些函数的学习,一定能让你在电脑绘图上得心应手。
相关文章:

SimpleCG绘图函数(9)--绘制各种线条
一、所有线段函数概述 可填充图形绘制函数都介绍完了,还有一些特殊线条的绘制将在本篇进行讲解。所有特殊线条函数如下所示,其中还有一个区域填充函数floodfill比较特殊,是配合线条函数使用的: //绘制一系列折线段 //折线段以一组…...

RISCV 6 RISC-V加载存储指令
RISCV 6 RISC-V加载存储指令 1 RV32I Load and Store Instructions1.1 LOAD instructions1.1.1 加载指令的指令格式1.1.2 加载指令在使用时需要注意的点 1.2 STORE instructions1.2.1 存储指令的指令格式1.2.2 存储指令在使用时需要注意的点 2 RV64 Load and Store Instruction…...

木叶飞舞之【机器人ROS2】篇章_第二节、turtlebot3安装
没有真实小车的情况下,利用gazebo的仿真,操作小乌龟来学习ros2。废话不多说,直接上命令。 Install Gazebo sudo apt install ros-humble-gazebo-*Install Cartographer 假如前一节未安装源码版本的cartographer,那就安装apt版本…...
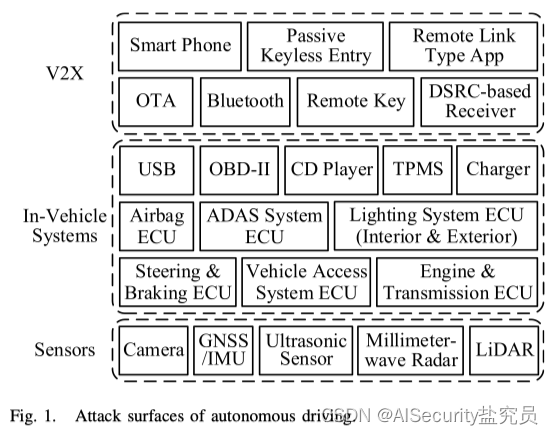
【论文阅读】自动驾驶安全的研究现状与挑战
文章目录 摘要1.引言1.1.自动驾驶安全1.2.攻击面1.3.内容和路线图 2.自动驾驶技术2.1.组成2.2.技术 3.传感器安全3.1.照相机3.2.GNSS(全球导航系统)/IMU(惯性测量单元)3.3.超声波传感器3.4.毫米波雷达3.5.激光雷达3.6.多传感器交叉…...
标签打印小工具 选择图片打印,按实际尺寸打印。可旋转图片
您可以尝试使用以下标签打印工具: 柯尼卡美能达标签打印机:功能齐全、易于使用的打印机,支持各种标签尺寸和类型。 赛门铁克标签打印机:高速打印、可靠性强的打印机,支持多种操作系统和软件。 齐柏林标签打印机&…...
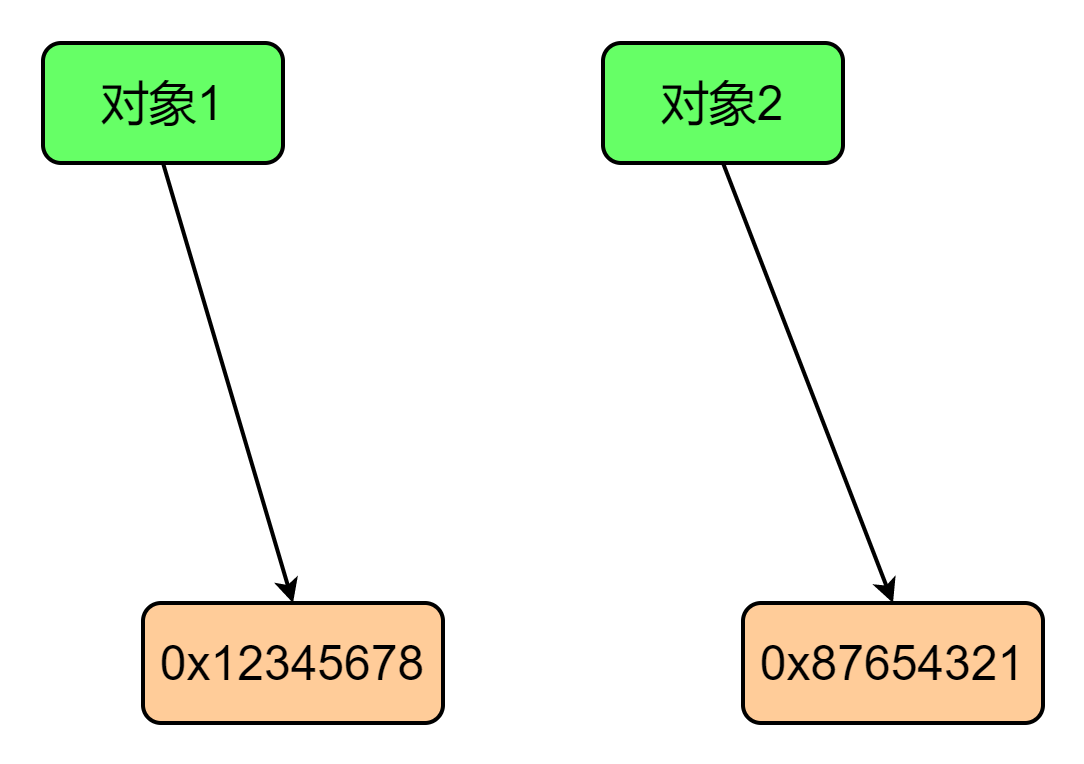
什么是深拷贝和浅拷贝?
面试回答 在计算机内存中,每个对象都有一个地址,这个地址指向对象在内存中存储的位置。当我们使用变量引用一个对象时,实际上是将该对象的地址赋值给变量。因此,如果我们将一个对象复制到另一个变量中国,实际上是将对象…...
安装docker服务及docker基本操作
一、docker安装(yum安装) 基于centos7 1.添加docker-ce 源信息 安装依赖包(yum-utils 提供了 yum-config-manager ,并且 device mapper 存储驱动程序需要device-mapper-persistent-data 和 lvm2) yum install yum-…...
)
【项目经验】:项目中下拉框数据太多造成页面卡顿(二)
一.项目需求 下拉框下拉列表数据是由后端返回的,而且他会变化,所以数据不是写死的而且数据量大。上一篇博客http://t.csdn.cn/sSNTa我们是用的数据懒加载的方式,这次我们使用远程搜索的方式解决这个问题。 二.用到的组件方法介绍 filterabl…...

Prompt本质解密及Evaluation实战(一)
一、基于evaluation的prompt使用解析 基于大模型的应用评估与传统应用程序的评估不太一样,特别是基于GPT系列或者生成式语言模型,因为模型生成的内容与传统意义上所说的内容或者标签不太一样。 以下是借用了ChatGPT官方的evaluation指南提出的对结果的具…...

linux 在系统已有python2版本下安装python3
方法一:使用包管理器安装 更新包索引: sudo apt update 安装Python3: sudo apt install python3 安装Python3的pip(如果你需要): sudo apt install python3-pip 验证Python 2和3的安装: pyt…...
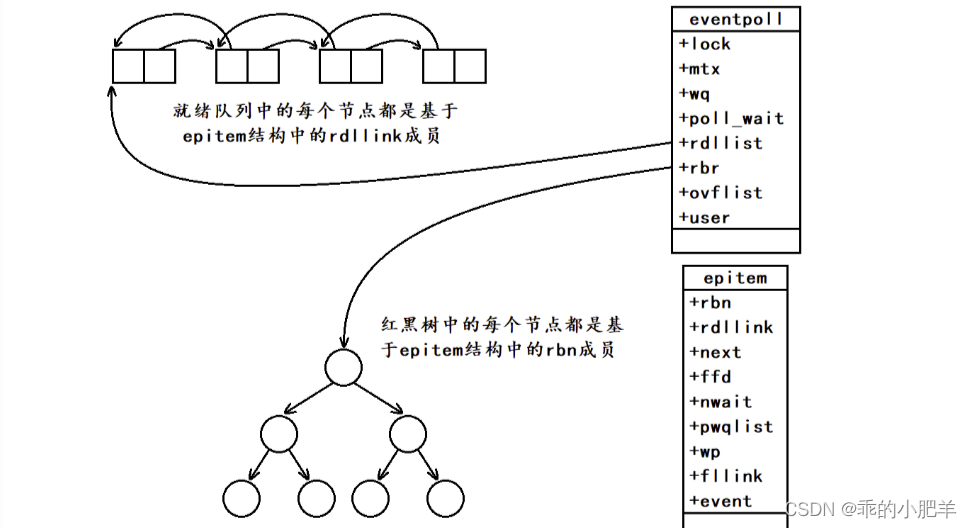
IO多路转接 ——— select、poll、epoll
select初识 select是系统提供的一个多路转接接口。 select系统调用可以让我们的程序同时监视多个文件描述符的上的事件是否就绪。 select的核心工作就是等,当监视的多个文件描述符中有一个或多个事件就绪时,select才会成功返回并将对应文件描述符的就绪…...
FPGA原理与结构——FIFO IP核原理学习
一、FIFO概述 1、FIFO的定义 FIFO是英文First-In-First-Out的缩写,是一种先入先出的数据缓冲器,与一般的存储器的区别在于没有地址线, 使用起来简单,缺点是只能顺序读写数据,其数据地址由内部读写指针自动加1完成&…...

【Linux操作系统】Linux中的信号回收:管理子进程的关键步骤
在Linux中,我们可以通过捕获SIGCHLD信号来实现对子进程的回收。当一个子进程终止时,内核会向其父进程发送SIGCHLD信号。父进程可以通过注册信号处理函数,并在处理函数中调用wait()或waitpid()函数来回收已终止的子进程。 文章目录 借助信号捕…...
Spark大数据分析与实战笔记(第一章 Scala语言基础-1)
文章目录 章节概要1.1 初识Scala1.1.1 Scala的概述1.1.2 Scala的下载安装1.1.3 在IDEA开发工具中下载安装Scala插件1.1.4 开发第一个Scala程序 章节概要 Spark是专为大规模数据处理而设计的快速通用的计算引擎,它是由Scala语言开发实现的,关于大数据技术…...

R语言03-R语言中的矩阵
概念 在R语言中,矩阵(Matrix)是一个二维的数据结构,由行和列组成,其中所有元素必须具有相同的数据类型。矩阵可以用于存储数值型数据,常用于线性代数运算、统计计算以及数据处理等领域。 代码示例 # 创建…...

“深入理解JVM:探索Java虚拟机的工作原理与优化技巧“
标题:深入理解JVM:探索Java虚拟机的工作原理与优化技巧 摘要:本文将深入探索Java虚拟机(JVM)的工作原理及优化技巧。我们将介绍JVM的架构和组成部分,解释JVM是如何将Java字节码转换为可执行代码的。我们还…...

SQL注入原理
SQL、SQL注入是什么? 结构化查询语言(Structured Query Language,SQL),是一种特殊的编程语言,用于数据库的标准数据查询。1986 年10 月美国国家标准协会对SQL 进行了规范后,以此作为关系型数据库系统的标准语言。1987 …...
PIL.Image和base64,格式互转
将PIL.Image转base64 ##PIL转base64 import base64 from io import BytesIOdef pil_base64(image):img_buffer BytesIO()image.save(img_buffer, formatJPEG)byte_data img_buffer.getvalue()base64_str base64.b64encode(byte_data)return base64_str将base64转PIL.Image …...
)
vue父子组件传值(v-model)
父组件使用v-model传值给子组件 <template><!-- 按钮 --> <el-button click"addMenu(new)">打开弹框</el-button><!-- 自定义组件,下面这两种写法都可以👇 --> <MediaDialog :name"name" v-model:visible&qu…...
Java接口详解
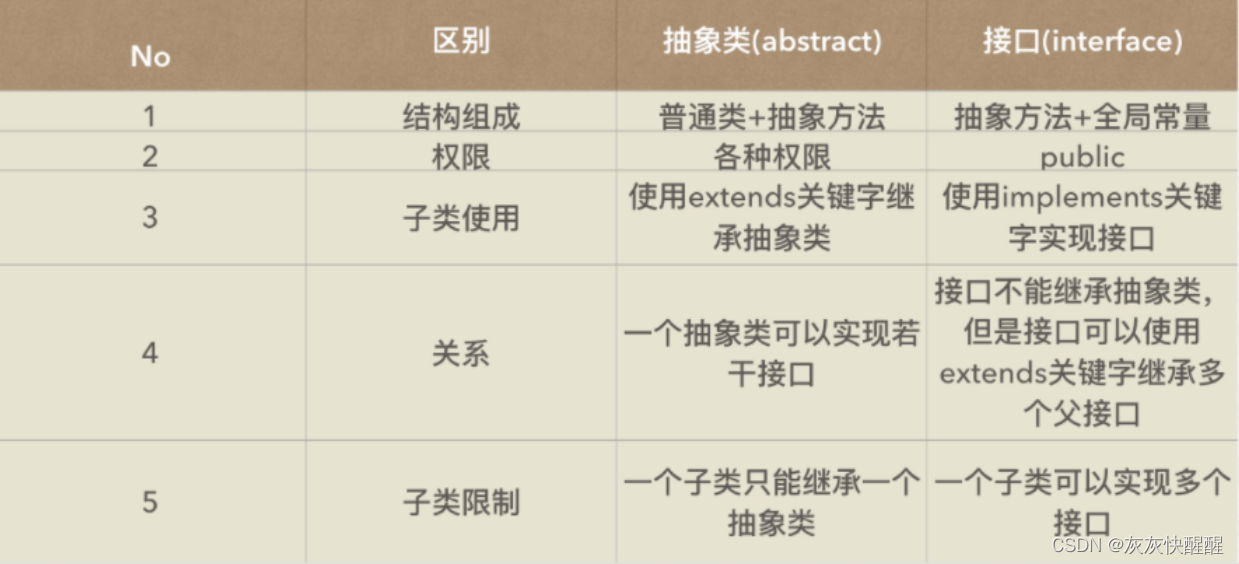
接口 接口的概念 在现实生活中,接口的例子比比皆是,比如:笔记本上的USB口,电源插座等。 电脑的USB口上,可以插:U盘,鼠标,键盘等所有符合USB协议的设备 电源插座插孔上,…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
