【线性DP】模型总结(terse版)
【线性DP】模型总结
最长上升子序列
DP法
dp[i]表示以i结尾的最长上升子序列的长度。
对于每个i,遍历j=1~i-1,若a[j] < a[i], 则dp[i] = max(dp[i], dp[j] + 1);
二分法
可以优化时间复杂度。
dp[]数组用来存储当前最长上升子序列。
若dp[]数组的最末尾的值小于当前原序列的值,则将这个值加入dp[]数组末尾。
否则,使用Lower_bound找到dp[]数组中第一个大于该值的元素,替换。
如果需要输出序列:定义s[]数组,记录下标,随dp[]数组更新。
最长公共子序列
定义dp[] []二维数组,表示a串以i结尾,b串以j结尾的最长公共子序列。
枚举i = 1 ~ a.size(), j = 1 ~ b.size().
若a[i - 1] == b[j - 1], dp[i] [j] = dp[i - 1] [j - 1] + 1;
否则 dp[i] [j] = max(dp[i - 1] [j], dp[i] [j - 1])。
最大子矩阵
首先遍历len=1~n,再将i从1遍历,确定j的值,得出一个len行n列的值,每一列对应相加,得到1行n列的序列,再求线性最大子段和。
得到的最大值就是Len行(从i到j)的最大子矩阵的值。
每次求都不断更新ans = max(ans, dp[i])。
最大正方形
给出一个01矩阵,求都是1的最大正方形的边长
dp[i] [j] 表示以x=i,y=j为右下角的最大正方形。 若a[i - 1] [j]、a[i] [j - 1]、a[i - 1] [ j - 1]均为1,则正方形的边长可以加一,即dp[i] [j] + 1。
否则,dp[i] [j] = min(dp[i - 1] [j]、dp[i] [j - 1]、dp[i - 1] [ j - 1])
题目:最大子矩阵
代码:AC代码
最大子段和
线性
定义dp[]一维数组,dp[i]表示以i结尾的最大字段和的值。
有两种情况:
1.独自成串:dp[i] = a[i];
2.与前一个元素连成串:dp[i] = dp[i - 1] + a[i];
合并得:dp[i] = max(dp[i - 1] + a[i], a[i])。
答案是dp[1~n]中最大值。
环形
依照上述方法,求出序列和、最大字段和、最小字段和。
答案 = max(和 - 最小字段和, 最大字段和)。
子集和问题
定义dp[] []bool类二维数组,dp[i] [j] 表示前i个数存在一个子集和等于j,答案就是dp[n] [M]。
s[]数组记录集合中元素。
若s[i] > j,则不能放入, dp[i] [j] = dp[i - 1] [j]。
否则, 放不放皆可,dp[i] [j] = (dp[i - 1] [j] || dp[i - 1] [j - s[i]])。
行走问题
类似于爬楼梯。
给出目标阶梯数和每步最多爬几层。
对于每个dp[i]表示走到第i层的步数总数,每次遍历j=i - k~i - 1,dp[i] += dp[j]。
答案就是dp[n]。
相关文章:
)
【线性DP】模型总结(terse版)
【线性DP】模型总结 最长上升子序列 DP法 dp[i]表示以i结尾的最长上升子序列的长度。 对于每个i,遍历j1~i-1,若a[j] < a[i], 则dp[i] max(dp[i], dp[j] 1); 二分法 可以优化时间复杂度。 dp[]数组用来存储当前最长上升子序列。 若dp[]数…...

conda 常用命令
conda 常用命令 一、创建环境二、删除环境三、环境重命名四 、查看环境列表五、进入某个虚拟环境六、退出当前环境七、查看当前虚拟环境下的所有安装包八、安装或卸载包(进入虚拟环境之后)九、分享虚拟环境十、源服务器管理十一、升级十二、卸载十三、卸载十四、pip…...

前端面试:【异步编程】Callback、Promise和Async/Await
嗨,亲爱的JavaScript探险家!在JavaScript开发的旅程中,你会经常遇到异步编程的需求。为了处理异步操作,JavaScript提供了多种机制,包括Callbacks、Promises和Async/Await。本文将深入介绍这些机制,让你能够…...
:Pandas的基础应用详解)
大数据(四):Pandas的基础应用详解
专栏介绍 结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来! 全部文章请访问专栏:《Python全栈教…...

计算机网络第3章(数据链路层)
计算机网络第3章(数据链路层) 3.1 数据链路层概述3.1.1 概述3.1.2 数据链路层使用的信道3.1.3 三个重要问题 3.2 封装成帧3.2.1 介绍3.2.2 透明传输3.2.3 总结 3.3 差错检测3.3.1 介绍3.3.2 奇偶校验3.3.3 循环冗余校验CRC(Cyclic Redundancy Check)3.3.…...

stm32之4.时钟体系
3.时钟体系(给单片机提供一个非常稳定的频率信号) ①可以使用三种不同的时钟源来驱动系统时钟(SYSCLK),CPU运行的频率为168MHZ; HSI(RC振荡器时钟,也就是高速内部时钟,一般来说很少用,因为精度…...
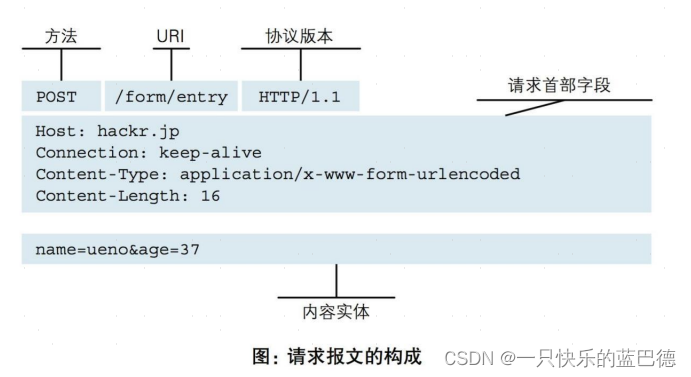
RPC和HTTP协议
RPC 全称(Remote Procedure Call),它是一种针对跨进程或者跨网络节点的应用之间的远程过程调用协议。 它的核心目标是,让开发人员在进行远程方法调用的时候,就像调用本地方法一样,不需要额外为了完成这个交…...

BUGFix:onnx -> TensorRT转换过程失败
先附上相关的onnx2trt的部分代码: def onnx2trt(onnx_path):logger trt.Logger(trt.Logger.ERROR)builder trt.Builder(logger)network builder.create_network(1 << int(trt.NetworkDefinitionCreationFlag.EXPLICIT_BATCH))parser trt.OnnxParser(netw…...

FFMPEG小白常用命令行
序列帧转H264视频 ffmpeg -r 60 -f image2 -s 1920x1080 -i fram%d.jpg -vcodec libx264 -crf 25 -pix_fmt yuv420p test.mp4 -vcodec h264 .\ffmpeg -r 60 -f image2 -s 1920x1080 -i %04d.jpeg -vcodec h264 test.mp4 %04d 表示用零来填充直到长度为4,i.e 000…...

个性定制还是纯粹简约:探寻界面选择背后的心理宇宙
在数码世界中,我们的界面选择成为了一张架起的桥梁,连接着个性的渴望与效率的追求。当我们面对个性化定制界面和极简版原装界面,我们仿佛站在了一座分岔路口,左右各有一片令人心驰神往的风景。究竟是走向五光十色的个性世界&#…...

【Java 高阶】一文精通 Spring MVC - 转发重定向(四)
👉博主介绍: 博主从事应用安全和大数据领域,有8年研发经验,5年面试官经验,Java技术专家,WEB架构师,阿里云专家博主,华为云云享专家,51CTO 专家博主 ⛪️ 个人社区&#x…...
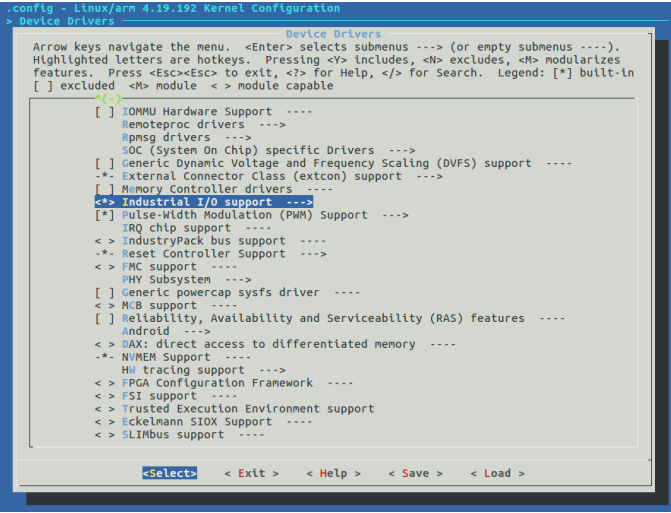
嵌入式Linux开发实操(十):ADC接口开发
#前言 ADC就是模数转换,可以用来接一些模拟量设备,所谓模拟量就是波形不是方波而是各种包络形状的波形的信号,比如电压、电流等电信号或压力、温度、湿度、位移、声音等非电信号,ADC就是将这些信号转换为数字方波信号,以便于信息传递的。 #ADC硬件设计 key按键连接了AD…...
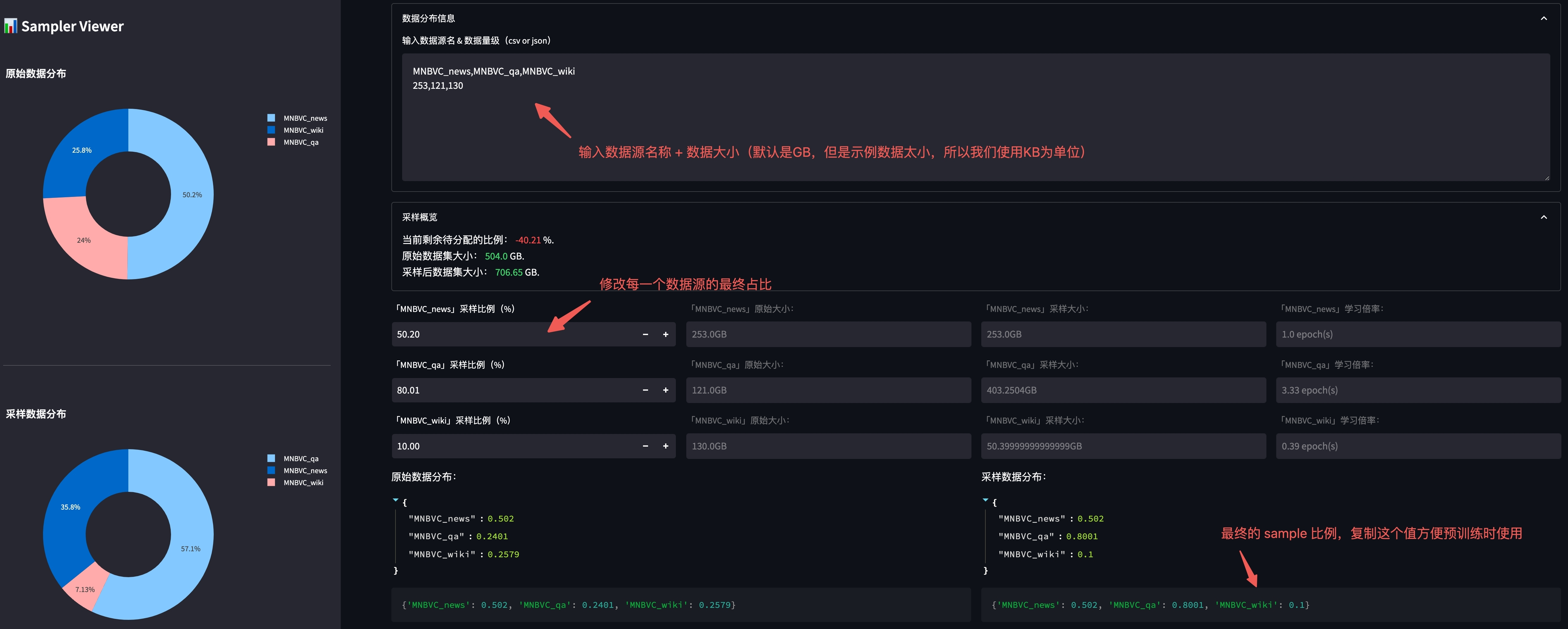
精进语言模型:探索LLM Training微调与奖励模型技术的新途径
大语言模型训练(LLM Training) LLMs Trainer 是一个旨在帮助人们从零开始训练大模型的仓库,该仓库最早参考自 Open-Llama,并在其基础上进行扩充。 有关 LLM 训练流程的更多细节可以参考 【LLM】从零开始训练大模型。 使用仓库之…...

数据采集:selenium 提取 Cookie 自动登陆
写在前面 工作需要,简单整理博文内容涉及 通过 selenium 实现自动登陆理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的&#x…...

[Go版]算法通关村第十三关黄金——数字数学问题之数论问题(最大公约数、素数、埃氏筛、丑数)
目录 题目:辗转相除法(求最大公约数)思路分析:辗转相除法(也叫欧几里得算法)gcd(a,b) gcd(b,a mod b)复杂度:时间复杂度 O ( n l o g ( m a x ) ) O(nlog(max)) O(nlog(max))、空间复杂度 O (…...
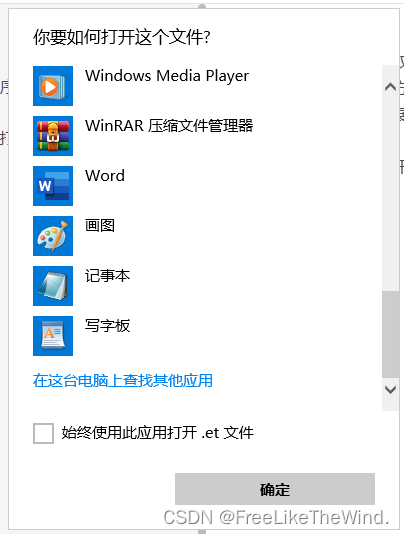
Qt双击某一文件通过自己实现的程序打开,并加载文件显示
双击启动 简述方法一方法二注意 简述 在Windows系统中,双击某类扩展名的文件,通过自己实现的程序打开文件,并正确加载及显示文件。有两种方式可以到达这个目的。 对于系统不知道的扩展名的文件,第一次打开时,需要自行…...

硬件产品的量产问题------硬件工程师在产线关注什么
前言: 产品开发测试无误,但量产缺遇到很多不良甚至DOA问题。 硬件开发过程中如何确保产线的治具、生产及硬件工程师在产线需要关注一些什么。 坚信:好的产品是要可以做出来的。 1、禁忌: 禁忌热插拔;禁忌测试不防呆…...
Vulnhub系列靶机--- Hackadmeic.RTB1
系列:Hackademic(此系列共2台) 难度:初级 信息收集 主机发现 netdiscover -r 192.168.80.0/24端口扫描 nmap -A -p- 192.168.80.143访问80端口 使用指纹识别插件查看是WordPress 根据首页显示的内容,点击target 点击…...
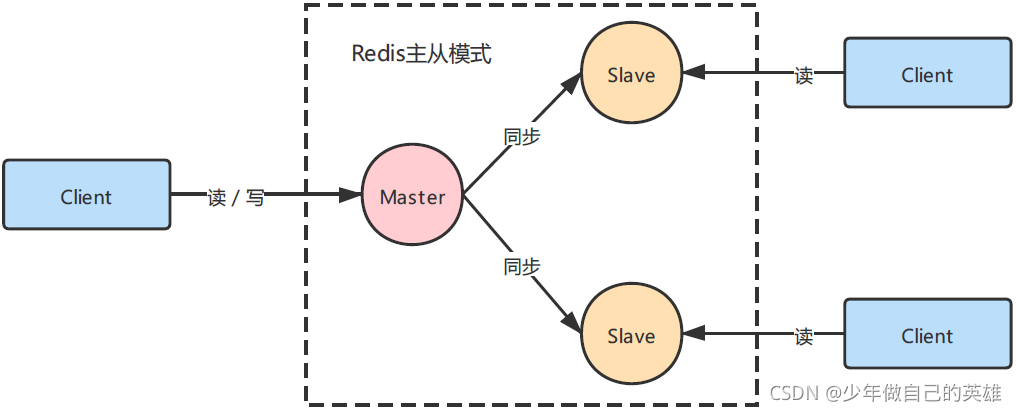
redis高级----------主从复制
redis的四种模式:单例模式;主从模式;哨兵模式,集群模式 一、主从模式 单例模式虽然操作简单,但是不具备高可用 缺点: 单点的宕机引来的服务的灾难、数据丢失单点服务器内存瓶颈,无法无限纵向扩…...

posgresql通过PL/pgSQL脚本统一修改某字段大小写
项目在做postgresql数据库适配时遇到了某些问题,需要统一将某个模式含id字段的全部表,将id字段由小写转换为大写,可以通过PL/pgSQL脚本实现。 先确保当前用户有足够的权限 DO $$ DECLARE current_table text;current_column text; BEGIN --…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
