20.图的遍历
目录
一. 深度优先遍历
二. 广度优先遍历
图的遍历算法和二叉树不同的是,图中可能存在回路,且图的任一顶点都可能与其它顶点相通,在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。为了避免重复访问,我们的解决思路是:设置辅助数组visited[n],用来标记每个被访问过的顶点。初始状态visited[i]都为0,当顶点i被访问,改visited[i]为1,防止被多次访问。
图的遍历算法主要有深度优先搜索(Depth_First Search——DFS)和广度优先搜索(Breadth_Frist Search———BFS)两种。
一. 深度优先遍历
基本思想:“一条道走到黑”,直到走不了往回退。
- 在访问图中某一起始顶点v后,由v出发,访问它的任一邻接顶点w_1(所以深度优先搜索操作实现可以不唯一);
- 再从w_1出发,访问与w_1邻接但还未被访问过的顶点w_2;
- 然后再从w_2出发,进行类似的访问,...
- 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点u为止。接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点。
- 如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;
- 如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止。
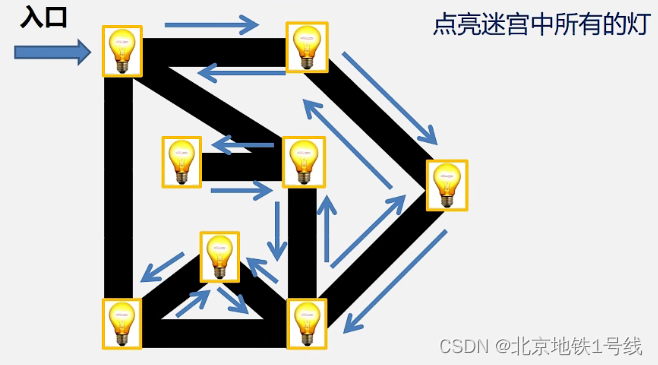

观察上面的访问路径,连通图的深度优先遍历类似于树的先根遍历。
下面讨论邻接矩阵表示的无向图深度优先遍历的实现:对无向图,邻接矩阵的每一行代表了这个点与其他点的连接情况。我们从左向右看哪一个元素不为零,且这个结点没被访问过(visited=0),就优先访问哪个结点,这样给定起点就能唯一确定一条深度优先的遍历路径。
void DFS(AMGraph G, int v){ //图G为邻接矩阵类型,v是起点cout<<v; visited[v] = true; //访问第v个顶点for(w = 0; w < G.vexnum; w++) //依次检查邻接矩阵v所在的行if((G.arcs[v][w]!=0)&&(!visited[w])) //路径存在,且w未被访问DFS(G, w); //w是v的邻接点,如果w未访问,则递归调用DFS
}
用邻接矩阵来表示图,遍历图中每一个顶点都要从头扫描该顶点所在的行,时间复杂度为O(n^2)。
用邻接表来表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n+e)。
结论:稠密图适于在邻接矩阵上进行深度遍历;稀疏图适于在邻接表上进行深度遍历。
二. 广度优先遍历
方法:从图的某一结点出发,首先依次访问该结点的所有邻接点Vi1, Vi2 ... Vin,再按这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点。重复此过程,直至所有顶点均被访问为止。

void BFS(Graph G, int v){ //按广度优先非递归遍历连通图G,起始点为vcout<<v; visited[v] = true; //访问第v个顶点InitQueue(Q); //辅助队列Q初始化,置空EnQueue(Q, v); //v进队while(!QueueEmpty(Q)){ //队列非空DeQueue(Q, u); //队头元素出队并置为ufor(w = FirstAdjVex(G,u); w>=0; w = NextAdjVex(G, u, w))if(!visited[w]){ //w为u的尚未访问的邻接顶点cout<<w; visited[w] = true;EnQueue(Q, w); //w进队}//if} //while
} //BFS
上述代码实现了广度优先搜索(Breadth First Search,BFS)算法。BFS是一种用于图的遍历算法,通过队列的方式依次访问图中的每个节点。
该代码中的BFS函数接受两个参数:图G和起始节点v。首先输出当前节点v的值,然后将该节点标记为已访问。接着,初始化一个队列Q,并将节点v入队。进入循环,直到队列Q为空为止。在循环中,从队列Q中出队一个节点u,然后遍历节点u的邻接节点w。如果节点w未被访问过,则输出节点w的值,将节点w标记为已访问,并将节点w入队。
在BFS函数中,visited数组用于记录每个节点是否已经被访问过。InitQueue(Q)用于初始化队列Q,EnQueue(Q, v)用于将节点v入队,DeQueue(Q, u)用于从队列Q中出队一个节点u。
FirstAdjVex(G,u)函数用于获取节点u的第一个邻接节点。它接受两个参数:图G和节点u。该函数会返回节点u的第一个邻接节点的索引值(或编号)。如果节点u没有邻接节点,则返回一个特定的标识值(比如-1)。而NextAdjVex(G, u, w)函数用于获取节点u在节点w之后的下一个邻接节点。它接受三个参数:图G、节点u和当前节点w。该函数会返回节点u在节点w之后的下一个邻接节点的索引值(或编号)。如果节点u在节点w之后没有更多的邻接节点,则返回一个特定的标识值(比如-1)。这两个函数的作用是帮助遍历节点u的邻接节点。通过调用FirstAdjVex(G,u)函数,可以获取节点u的第一个邻接节点,然后通过调用NextAdjVex(G, u, w)函数,可以获取节点u在当前邻接节点w之后的下一个邻接节点,以此类推,直到遍历完所有的邻接节点。
通过调用BFS函数,可以遍历图中所有与起始节点v连通的节点,且按照广度优先的顺序进行访问。
相关文章:

20.图的遍历
目录 一. 深度优先遍历 二. 广度优先遍历 图的遍历算法和二叉树不同的是,图中可能存在回路,且图的任一顶点都可能与其它顶点相通,在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。为了避免重复访问,我们的解决思…...

ARM DIY(一)电源、SD卡座、SOC 调试
文章目录 前言加热台焊接热风枪吹焊电烙铁补焊电源调试SD 卡座调试DRAM 电路调试串口电路调试SOC 调试成品 前言 之前打样的几块 ARM 板,一直放着没去焊接。今天再次看到,决定把它焊起来。 加热台焊接 为了提高焊接效率,先使用加热台焊接…...

数学建模知识之小白入门篇
数学建模知识--小白入门篇 一、数学模型的定义二、建立数学模型的方法和步骤1. 模型准备2. 模型假设3. 模型构成4. 模型求解5. 模型分析 三、数模竞赛出题的指导思想四、竞赛中的常见题型1. 实际问题背景2.若干假设条件3.要求回答的问题 五、提交一篇论文…...
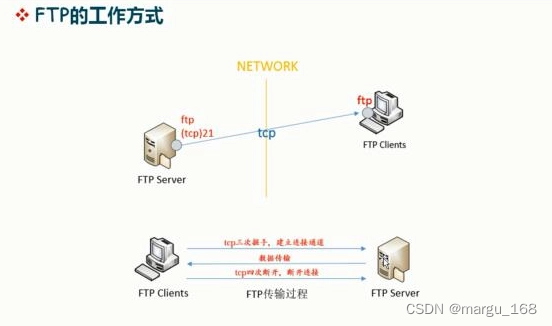
【日常积累】Linux下ftp服务安装
概述 FTP是一种在互联网中进行文件传输的协议,基于客户端/服务器模式,默认使用20、21号端口,其中端口20用于进行数据传输,端口21用于接受客户端发出的相关FTP命令与参数。FTP服务器普遍部署于内网中,具有容易搭建、方…...

确定了,TikTok将于9月12日正式关闭美国半闭环
外媒报道称,TikTok已对其官网的常见问题页面进行了更新。消息显示,其在美国和英国市场运营的半封闭模式将于9月12日正式结束,并将全力推进TikTok闭环小店业务。尽管我们早在本月初就获悉了这一消息,但实际得知后仍不免有些感慨。曾…...

ATFX汇评:英国7月零售销售年率大降,GBPUSD仍未升破1.3000
ATFX汇评:7月季调后零售销售年率,最新值-3.2%,前值-1.6%,降幅扩大;7月季调后核心零售销售年率,最新值-3.4%,前值-1.6%,降幅扩大。零售销售综合衡量除服务业外包括所有主要从事零售业…...
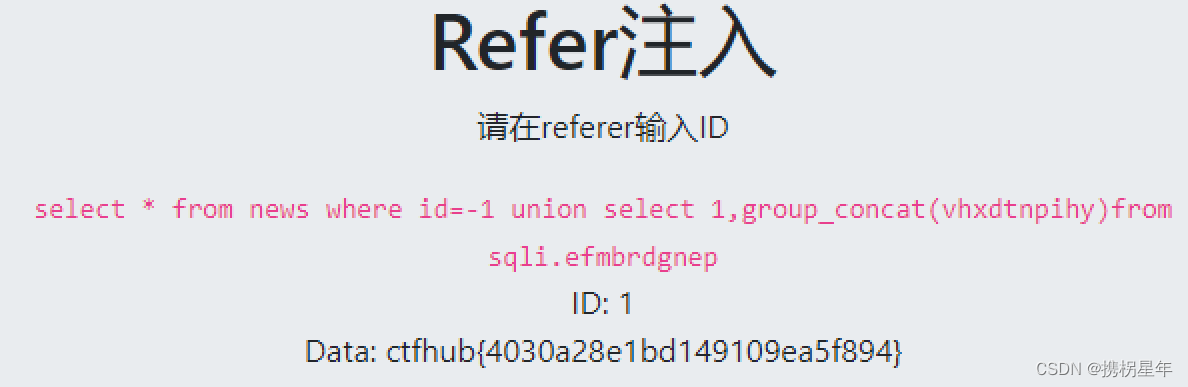
CTFhub-sqli注入-Referer注入
在最后添加 Referer: (注意 R 大写, Referer后面是 :,Content-Length: 与 Referer: 之间没有空行) 1 2 3 1 union select 1,database() -1 union select 1,database() -1 union select 1,group_concat(table_name)from information_sche…...
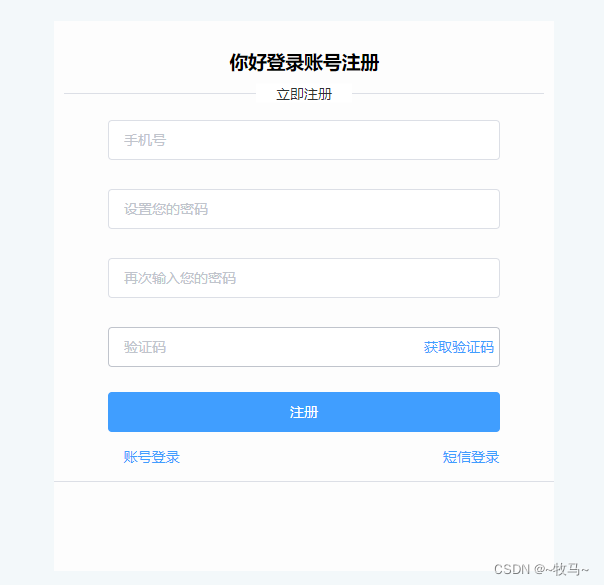
【案例】登录注册
<template><div class"loginhome"><Header :butShow"butShow"></Header><div class"formdiv"><div style"text-align:center;padding:10px;"><h3>你好登录账号{{ stauts 3? 注册:登录 }}…...
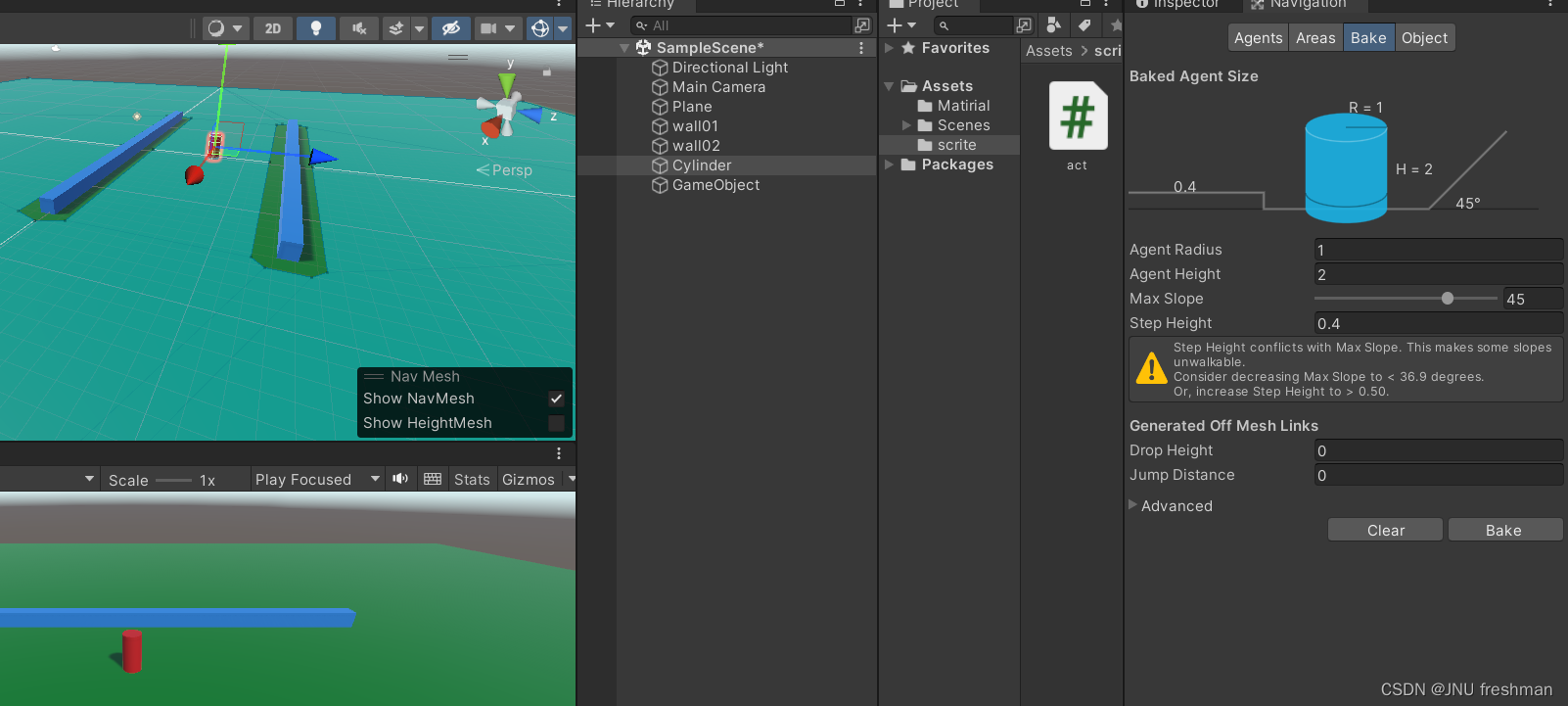
Unity 物体的运动之跟随鼠标
你想让鼠标点击哪里,你的运动的对象就运动到哪里吗? Please follow me ! 首先,你要先添加一个Plane ,以及你的围墙,你的移动的物体 想要实现跟随鼠标移动,我们先创建一个脚本 using System.Collections; using Syst…...
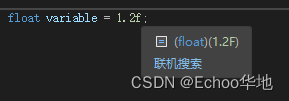
C++基础Ⅱ变量
目录儿 4 变量4.1 原始数据类型字符 char整型 short整型 int整型 long整型 long long单精度浮点型 float双精度浮点型 double布尔型 bool 4.2 sizeof 关键字 5 指针和引用 4 变量 4.1 原始数据类型 原始数据类型是构建C程序的最基础数据类型 所有数据都是基于这些原始数据类型…...

Linux管理SpringBoot应用shell脚本实现
Liunx系统如何部署和管理SpringBoot项目应用呢?最简单的方法就是写个shell脚本。 Spring Boot是Java的一个流行框架,用于开发企业级应用程序。下面我们将学习如何在Linux服务器上部署Spring Boot应用,并通过一个脚本实现启动、停止、重启等操…...

一篇搞懂浏览器的工作原理(万字详解)
摘要 本文是学习极客时间上的课程,进而整理出的浏览器工作原理。 第一部分:浏览器的进程和线程 (1)进程和线程的区别? 在浏览器中,各个进程负责处理自己的事情,而不同的进程中,也…...
)
C语言调用python训练的机器学习模型(项目需求轻体量)
问题描述 机器学习模型基本上都是python下的实现与使用,有关C如何调用训练好的模型或是C实现模型的相关教程相对较少 同时,项目需求整个模型大小尽可能小,大概在几十Kb 由于是表格类型的数据,因此主要考虑树模型 一般而言&#…...

get和post请求的区别以及post请求的url参数问题
1.主要区别 1.GET请求方法有以下几个特点: 默认的请求方法;GET请求通常用于获取信息,所以应该是安全的、幂等的;请求数据表现在URL上,以名称/值的形式发送。对请求的长度有限制;在IE和Opera等浏览器会产生…...

android NullPointerException externalCacheDir
先看代码: fun Context.getMyCacheDir(): String {return externalCacheDir!!.absolutePath "/my_cache" }如上代码,在某些手机可能会出现crash。 原因详细阅读api,注意他有一个大大的注解Nullable: Nullablepublic a…...
设计模式-过滤器模式(使用案例)
过滤器模式(Filter Pattern)或标准模式(Criteria Pattern)是一种设计模式,这种模式允许开发人员使用不同的标准来过滤一组对象,通过逻辑运算以解耦的方式把它们连接起来。这种类型的设计模式属于结构型模式…...
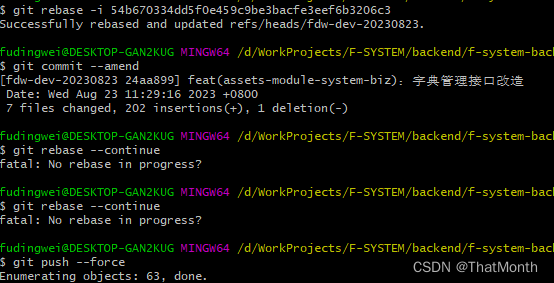
成功解决修改已经push到远程git仓库的commit message
1.使用 Git 命令行进入要修改的项目目录。 2.运行 git log 命令查看提交历史,找到要修改的提交的哈希值(commit hash)。 3.运行 git rebase -i <commit hash> 命令,将 <commit hash> 替换为要修改的提交的哈希值。这将…...

Ubuntu18.04 交叉编译openssl-1.1.1
源码下载地址: openssl 此处使用的是openssl-1.1.1-pre5.tar.gz 解压: $tar -zxvf openssl-1.1.1-pre5.tar.gz $cd openssl-1.1.1-pre5/ 执行配置生成Makefile: $./config no-asm shared --prefix$PWD/__install 或者 $./config no-asm shared no-…...

七夕学算法
目录 P1031 [NOIP2002 提高组] 均分纸牌 原题链接 : 题面 : 思路 : 代码 : P1036 [NOIP2002 普及组] 选数 原题链接 : 题面 : 思路 : 代码 : P1060 [NOIP2006 普及组] 开心的金明 原题链接 : 题面 : 思路 : 01背包例题 : 代码 : P1100 高低位交换 原题…...
)
在C++中利用rapidjson实现Python中的字典(Dict)
python 中的dict如下: Dicts = {"Stain":{"ResultType": "Physics","Results": [{"Key": "KeyPoints","Title": "瑕疵区域","Unit": "","Value": stainlist…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
