2023 CCPC 华为云计算挑战赛 hdu7399 博弈,启动!(图上博弈/枚举+逆向有向图sg函数)
题目
给定t(t<=200)组样例,
每次给定一个n(n<=300)个左边的点m(m<=300)个右边的点的二分图,图无重边
所有边总量不超过5e5
初始时棋子可以被放置在任意一个点上,
若被放置在左边,则Alice先走;被放置在右边,则Bob先走
每次可以选择一个当前点有出边的点,走到那个点上,如果当前点没有出边,则游戏结束
Alice想访问所有点无数次,Bob想阻止Alice这么做,双方均采取最优策略
问Alice是否有必胜策略(Alice可以指定起点在哪里)
思路来源
heltion+蔡老师
题解
问题等价于,
只要Bob能找到一个点,使Alice不能无限次经过,则Bob胜,否则Alice胜
称这样的点为防御点,
n=300,所以考虑枚举防御点
对于枚举的防御点,先判断一下可达性,如果有点到不了防御点,则Alice全局必败
防御点是一个终态点,如果Alice不能到防御点,则Bob不能去指向防御点的点,以此类推…
已知终态不知起始态,其实与期望dp类似,启发我们建反图后从防御点拓扑排序
然后考虑类似拓扑排序的更新流程,实际就是sg函数的思想,
初始时,将防御点放入队列,
对二分图上的点,每个点计算一个dp值,
如果防御点位于左侧,则Alice到这个点就视为(在只考虑这个防御点时)获胜,置dp值为1
如果防御点位于右侧,则Bob到这个点就视为失败,置dp置为0
如果一个点的所有下游(反图的上游)都是对方的必胜点,则这个点是必败点
如果一个点的所有下游(反图的上游)存在对方的必败点,则这个点是必胜点
如果一个点确定了必胜/必败态,就将这个点放入队列,直至更新完所有点
跑完这一轮后,Alice必败&Bob必胜的起点需要被排除
此时,有一些点可能是没被更新过的,即拓扑排序中的环,
这些点的特性是:
1. 不存在下游是对方的必败点
2. 存在一部分下游点是对方的必胜点,
3. 另一部分下游是状态未确定的点
那如果Alice和Bob在这些点上玩的话,都只会走向状态未确定的点,使Alice永远走不到防御点
所以这些状态未确定的点,也需要被过滤排除
枚举完一个防御点就会过滤掉一些点,
枚举完所有点后,没被过滤掉的点,就是Alice的必胜起点,若不存在则Bob必胜
其实感觉是很典的拓扑图上sg问题
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,ll> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=605;
int T,n,m,u,v,k,c,dp[N],deg[N],d[N];
bool no[N],can[N];
vector<int>e[N];
void add(int u,int v){e[v].pb(u);deg[u]++;
}
bool L(int x){return x<n;
}
bool sol(int s){memset(dp,-1,sizeof dp);for(int i=0;i<n+m;++i)can[i]=0,d[i]=deg[i];queue<int>q;q.push(s);dp[s]=L(s);//点s表示GG想走到这里YY不想走到这里,位于左侧GG赢,位于右侧YY输can[s]=1;while(!q.empty()){int u=q.front();q.pop();for(auto &v:e[u]){can[v]=1;--d[v];if(~dp[v])continue;if(dp[u]==0)dp[v]=1;if(dp[u]==1 && !d[v])dp[v]=0;if(~dp[v])q.push(v);}}for(int i=0;i<n+m;++i){if(!can[i])return 0;if(L(i) && dp[i]==0)no[i]=1;if(!L(i) && dp[i]==1)no[i]=1;if(dp[i]==-1)no[i]=1;}return 1;
}
bool solve(){for(int i=0;i<n+m;++i){if(!deg[i])return 0;}memset(no,0,sizeof no);for(int i=0;i<n+m;++i){if(!sol(i))return 0;}for(int i=0;i<n+m;++i){if(!no[i])return 1;}return 0;
}
int main(){scanf("%d",&T);while(T--){scanf("%d%d",&n,&m);for(int i=0;i<n+m;++i){e[i].clear();deg[i]=0;}for(int i=0;i<n;++i){scanf("%d",&k);for(int j=1;j<=k;++j){scanf("%d",&v);add(i,n+v);}}for(int i=0;i<m;++i){scanf("%d",&k);for(int j=1;j<=k;++j){scanf("%d",&v);add(n+i,v);}}puts(solve()?"Yes":"No");}return 0;
}相关文章:
)
2023 CCPC 华为云计算挑战赛 hdu7399 博弈,启动!(图上博弈/枚举+逆向有向图sg函数)
题目 给定t(t<200)组样例, 每次给定一个n(n<300)个左边的点m(m<300)个右边的点的二分图,图无重边 所有边总量不超过5e5 初始时棋子可以被放置在任意一个点上, 若被放置在左边,则Alice先走;被放置在右边&a…...

Unity之 Vector3 的详细介绍以及方法的介绍
文章目录 总的介绍小试牛刀相关的描述的参数看个小例子 总的介绍 当涉及到Unity中的Vector3类时,以下是一些常用的方法和操作: magnitude 方法:返回向量的长度。 float length vector.magnitude;sqrMagnitude 方法:返回向量的平…...
Postgresql部署及简单操作
目录 1、介绍 2、什么是PostgreSQL 3、PostgreSQL 的特点 4、数据库定为 5、环境准备 6、编译安装 6.1 安装依赖包 6.2 下载安装包 6.3 创建用户 6.4 创建 postgresql数据目录并授权 6.5 上传压缩包并解压 6.6 编译postgresql源码 6.7 配置环境变量 6.8 初始化数…...

rabbitmq集群搭建
升级步骤 1.升级包上传 1.1上传erlang、rabbitmq安装包 创建对应升级目录 将安装包otp_src_22.1.7.tar.gz上传到新创建的目录下 将安装包rabbitmq-server-generic-unix-3.8.9.tar.xz上传到新创建的目录下 1.2 执行解压命令tar -zxvf otp_src_22.1.7.tar.gz xz -d rabbitmq-s…...

C++ 二叉搜索树的概念特性
1. 二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树 ,或者是具有以下性质的二叉树 : 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 若它的右子树不为空,则右子树上所有节点的值都大…...
7、Spring_AOP
一、Spring AOP 简介 1.概述 对于spring来说,有三大组件,IOC,ID,AOP aop概述:AOP(Aspect Oriented Programming)面向切面编程。 作用:不改变原有代码设计的基础上实现功能增强 例子 传统打印日志 使用…...
QChart:数据可视化(用图像形式显示数据内容)
1、数据可视化的图形有:柱状/线状/条形/面积/饼/点图、仪表盘、走势图,弦图、金字塔、预测曲线图、关系图、数学公式图、行政地图、GIS地图等。 2、在QT Creator的主页面,点击 欢迎》示例》右侧输入框 输入Chart,即可查看到QChar…...
【python】Leetcode(primer-set)
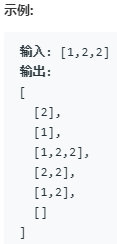
文章目录 78. 子集(集合的所有子集)90. 子集 II(集合的所有子集) 更多 leetcode 题解可参考:【Programming】 78. 子集(集合的所有子集) 给定一组不含重复元素的整数数组 nums,返回…...
【LVS集群】
目录 一、集群概述 1.负载均衡技术类型 2.负载均衡实现方式 二、LVS结构 1.三层结构 2.架构对象 三、LVS工作模式 四、LVS负载均衡算法 1.静态负载均衡 2.动态负载均衡 五、ipvsadm命令详解 1. -A 2. -D 3. -L 4. -a 5. -d 6. -l 7. -t 8. -s 9. -r 10. -…...

软考高级系统架构设计师系列之:论文题目类型、论文考试大纲、历年考试论文真题汇总、论文写作原则、论文写作常见问题、论文评分标准
软考高级系统架构设计师系列之:论文题目类型、论文考试大纲、历年考试论文真题汇总、论文写作原则、论文写作常见问题、论文评分标准 一、论文写作概述二、论文题目类型三、论文考试大纲1.系统建模2.软件架构设计3.系统设计4.分布式系统设计5.系统的可靠性分析与设计6.系统的安…...

完整的application.xml
<!-- 资源文件配置 --><beans profile"dev"><bean class"com.ningpai.util.CustomPropertyPlaceholderConfigurer"><property name"locations"><list><value>classpath:/com/ningpai/web/config/dev/jdbc.p…...

C语言:运算符优先级
一、优先级(常使用的运算符) 见表格 二、注意 总体原则:算术运算符 > 关系运算符 > 逻辑运算符 > 赋值运算符 同一级别下的运算符的运算次序由表达式的结合方向决定 运算符注释级别( )圆括号1[ ]数组下标1后置后置2后置--后置--2前置…...

Android GreenDao数据库升级(附Demo)
前言 大家好久不见,一转眼马上八月份下旬了,最近由于工作比较忙,没时间给大家更新博文。百忙之中抽出时间,给大家来更新一篇关于GreenDao3数据库的升级。 关于GreenDao的详细介绍以及一些逻辑性的增、删、改、查等,可以…...

剑指 Offer 32 - III. 从上到下打印二叉树 III
目录 使用函数实现 使用双端队列实现 请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。 例如: 给定二叉树: [3,9,20,nu…...
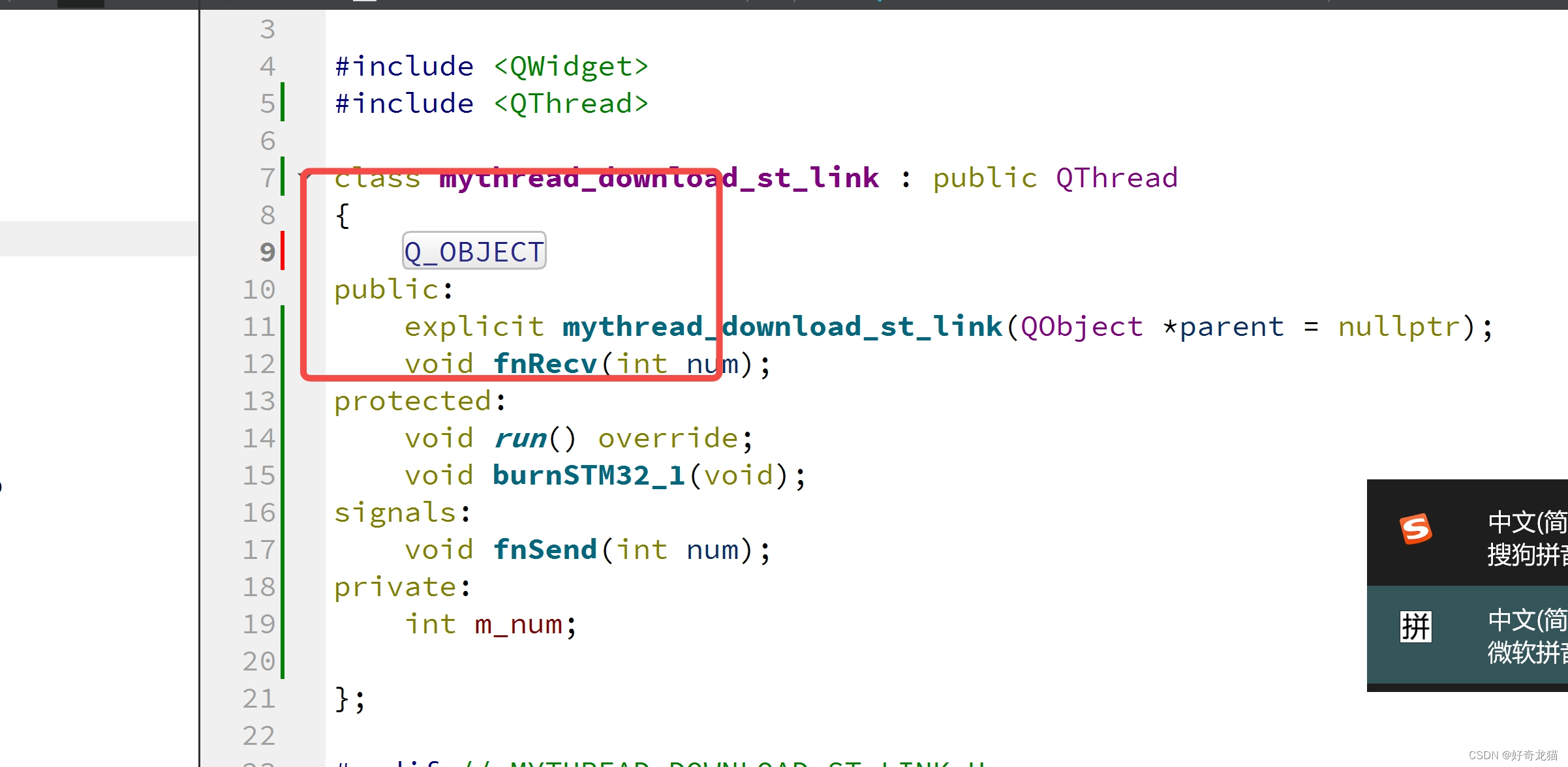
【QT5-自我学习-线程qThread移植与使用-通过代码完成自己需要功能-移植小记3】
【QT5-自我学习-线程qThread移植与使用-通过代码完成自己需要功能-移植小记3】 1、前言2、实验环境3、自我总结(1)文件的编写(2)信号与槽的新理解(3)线程数据的传递 4、移植步骤第一步:添加新文…...
后端开发12.商品模块
概述 简介 商品模块这个设计的非常复杂 效果图 数据库...

/usr/bin/containerd: Operation not permitted
问题 今天在重启docker程序的时候一直启动不起来,通过systemctl status docker和jourctl -xu docker也没有发现什么有用的报错信息,无奈只好查看/var/log/message,发现以下错误提示: Started containerd container runtime Start…...
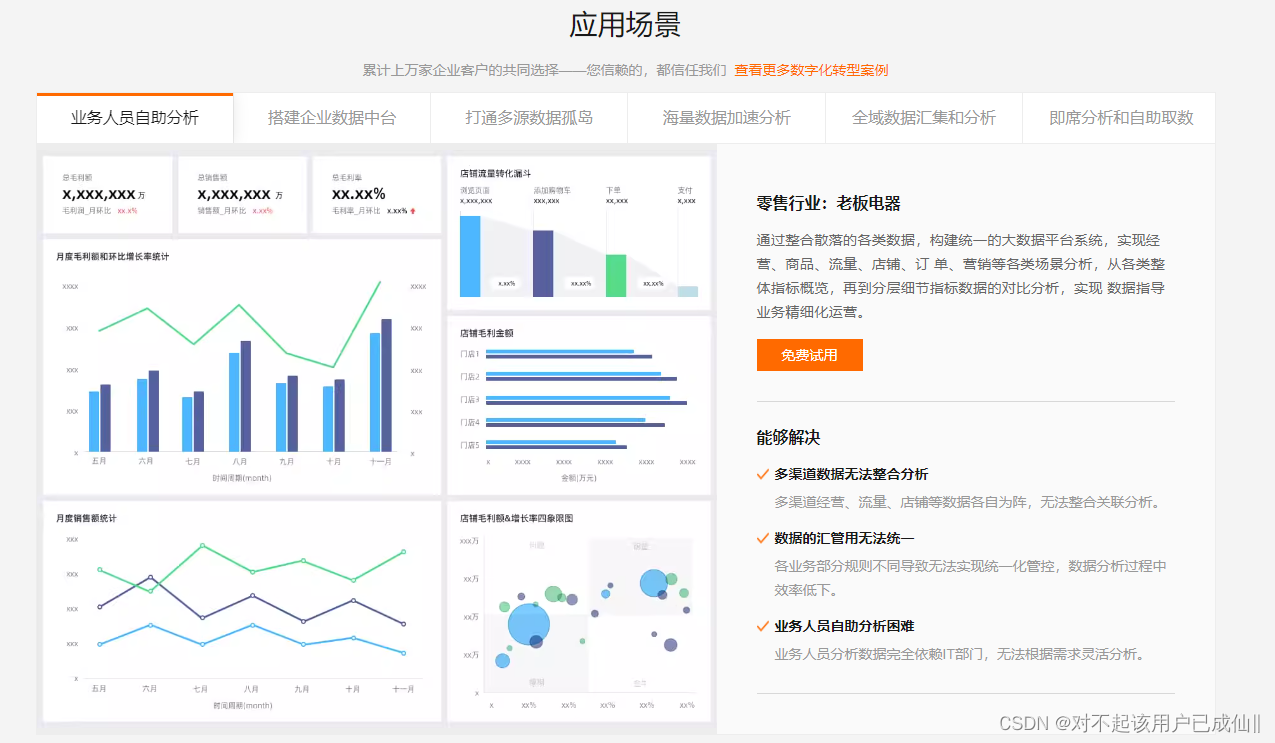
分析商务报表使用什么工具?
传统的BI分析商务报表存在的问题 随着数字化转型的深入推进,企业面临着海量数据的挑战和机遇。数据是企业的重要资产,能够帮助企业洞察市场动态、优化业务流程、提升客户满意度、创造竞争优势。然而,传统的BI(商业智能࿰…...

nginx文件配置
在部署前后端分离项目时,当前端和后端不在一个服务器上时,需要在前端服务器上下载nginx并配置 #hkdp-front-test 前端服务器 xxx.xxx.x.69 前端项目端口号9528,监听文件夹 /home/apps/vue/hkdp-manager 配置如下 server{ …...

视频云存储/安防监控EasyCVR视频汇聚平台如何通过角色权限自行分配功能模块?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。音视频流媒体视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
