(AcWing) 任务安排(I,II,III)
任务安排I:
有 N 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这 N 个任务分成若干批,每一批包含连续的若干个任务。
从时刻 0 开始,任务被分批加工,执行第 i 个任务所需的时间是 Ti。
另外,在每批任务开始前,机器需要 S 的启动时间,故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 Ci。
请为机器规划一个分组方案,使得总费用最小。
输入格式
第一行包含整数 N。
第二行包含整数 S。
接下来 N 行每行有一对整数,分别为 Ti 和 Ci,表示第 i 个任务单独完成所需的时间 Ti 及其费用系数 Ci。
输出格式
输出一个整数,表示最小总费用。
数据范围
1≤N≤5000,
0≤S≤50,
1≤Ti,Ci≤100
输入样例:
5
1
1 3
3 2
4 3
2 3
1 4
输出样例:
153#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N = 5010;
ll sumt[N],sumc[N],f[N];
//sumt[N]时间前缀和
//sumc[N]费用前缀和
//f[N]是将前i个任务处理完的所有方案的集合
ll n,s;int main()
{cin>>n>>s;for(int i=1;i<=n;i++){int t,c;cin>>t>>c;sumt[i] = t + sumt[i-1];sumc[i] = c + sumc[i-1];}memset(f,0x3f,sizeof f);//预防下面求最小值出错,先初始化为无穷大f[0] = 0;//前0个任务处理完的方案数自然为0for(int i=1;i<=n;i++){for(int j=0;j<i;j++){f[i] = min(f[i],f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]));}}cout<<f[n]<<endl;return 0;
} 
AcWing 300. 任务安排1【线性DP+费用提前计算思想】 - AcWing
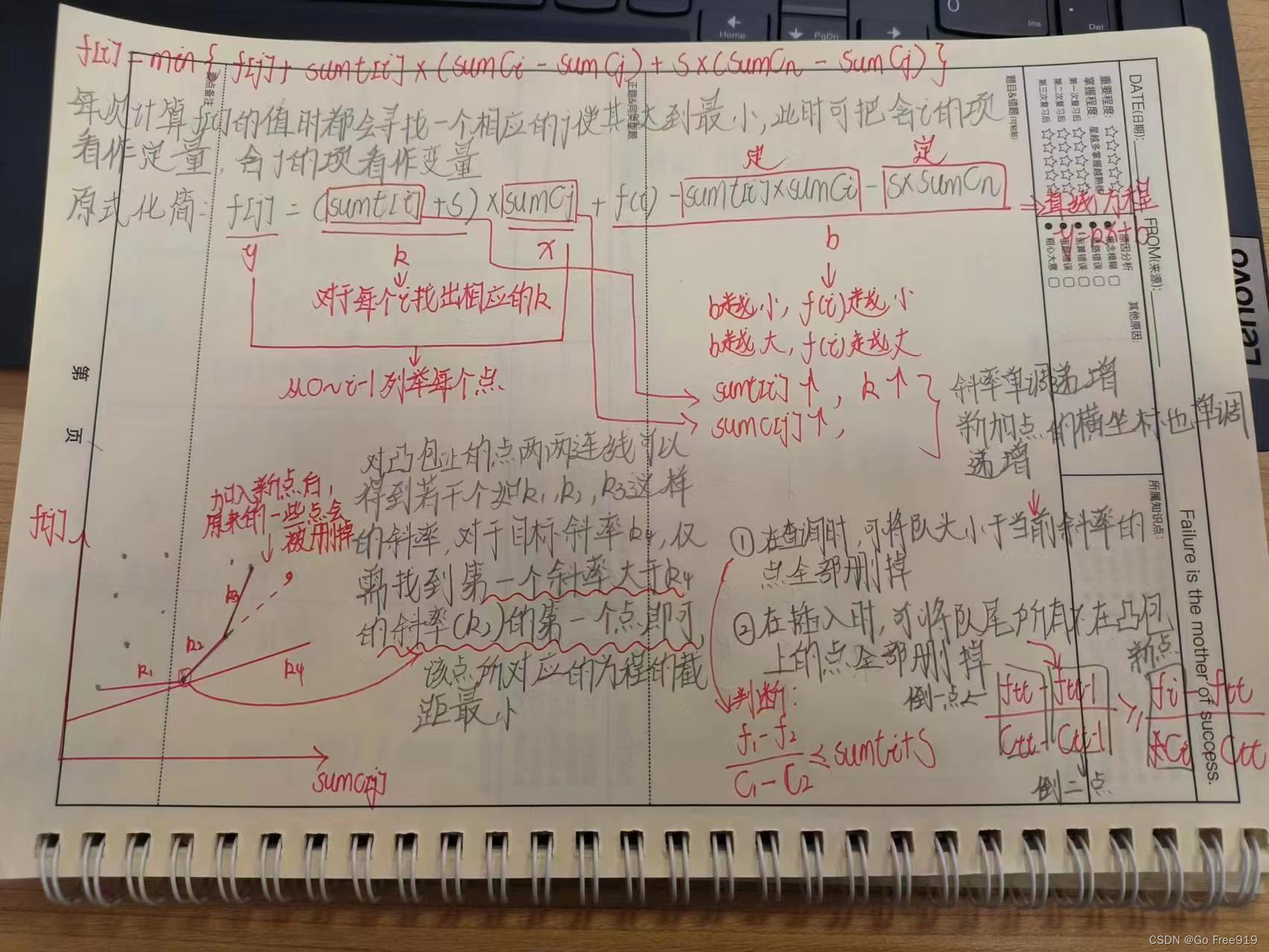
任务安排II:斜率优化DP
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;typedef long long ll;
const int N = 300010;
int n,s;
ll c[N],t[N],f[N],q[N];int main()
{cin>>n>>s;//读入数据计算时间和代价的前缀和for(int i=1;i<=n;i++){int a,b;cin>>a>>b;c[i] = c[i-1]+b;t[i] = t[i-1]+a;}int hh=0,tt=0; //hh是队头,tt的队尾q[0] = 0; //数组q表示的是队列,队列一开始存在(0,0)点for(int i=1;i<=n;i++){//将小于等于目标斜率的点全部删掉 (删除的是组成斜率的两个点中的第一个点)while(hh<tt&&(f[q[hh+1]]-f[q[hh]])<=(t[i]+s)*(c[q[hh+1]]-c[q[hh]])) hh++;//对头的元素就是我们所求的f[i]最小的点int j = q[hh];//代入公式f[i] = f[j] - (t[i]+s)*c[j]+t[i]*c[i] + s*c[n];//计算完后插入新的点,插入前应该将队尾所有不在凸包上的点均删掉while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]])) tt--;q[++tt] = i;}cout<<f[n]<<endl;
}
AcWing 301. 任务安排2【斜率优化DP模板】 - AcWing
相关文章:

(AcWing) 任务安排(I,II,III)
任务安排I: 有 N 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。 机器会把这 N 个任务分成若干批,每一批包含连续的若干个任务。 从时刻 0 开始,任务被分批加工,执行第 i 个任务所需的时间是 Ti。 另外&#x…...

Excel筛选后复制粘贴不连续问题的解决
一直以来都没好好正视这个问题认真寻求解决办法 终于还是被需求逼出来了,懒人拯救世界[doge] 一共找到两个方法,个人比较喜欢第二种,用起来很方便 Way1:CtrlG定位可见单元格后使用vlookup解决(感觉不定位直接公式向下…...

【SCSS变量】$ | | var | @for | @include | @function | @each 等常用方法使用
SCSS优点:编写清晰、无冗余、语义化的CSS,减少不必要的重复工作 1、变量声明($)和使用2、使用 & 代替父元素3、在HTML中使用 :style{--name: 动态值}自定义属性,在SCSS中用var(--name)函数绑定动态变量值ÿ…...

iOS 17 及 Xcode 15.0 Beta7 问题记录
1、iOS 17 真机调试问题 iOS 17之后,真机调试Beta版本必须使用Beta版本的Xcode来调试,用以前复制DeviceSupport 方式无法调试,新的Beta版本Xcode中,已经不包含 iOS 17目录。如下图: 解决方案: 1&#x…...
docker-maven-plugin直接把镜像推到私有仓库
接着上篇 推送到本地docker 我们已经把服务做成镜像推到docker,也可以通过docker login 私有地址,去push。麻烦 直接上代码 1、pom改动 <properties><docker.registry>eco-registry.XXX.com</docker.repostory><docker.registry…...

2023年机器学习项目—布匹缺陷检测
2023年机器学习项目———布匹缺陷检测 测试环境: CPU : 12th Gen Intel Core™ i7-12700H 2.70 GHz GPU : NVIDIA RTX3070Ti RAM : 32GB Matlab R2020a (Deep Learning Tools) 注 :Data文件过大 未上传 一.神经网络概述 1. 卷积神经网络概念 人工神经网络(Artific…...
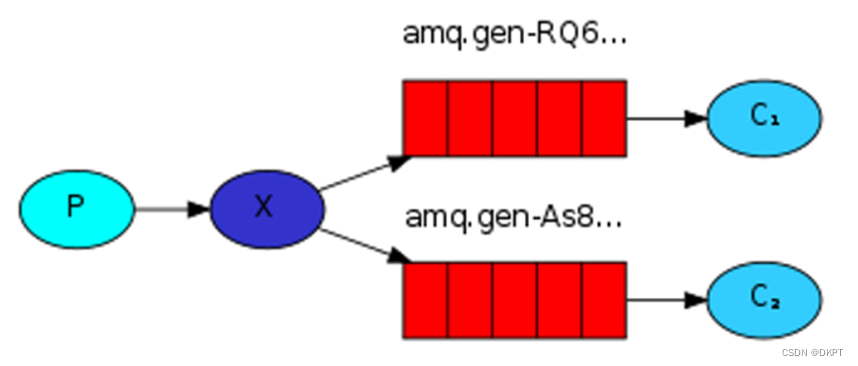
RabbitMQ---订阅模型分类
订阅模型分类 在之前的模式中,我们创建了一个工作队列。 工作队列背后的假设是:每个任务只被传递给一个工作人员。 在这一部分,我们将做一些完全不同的事情 - 我们将会传递一个信息给多个消费者。 这种模式被称为“发布/订阅”。 订阅模型示意…...
pycharm添加虚拟环境以及虚拟环境安装pytorch
file、settings、interpreter、add interpreter、add local interpreter 记住不要勾选inherit,不然会把主环境的东西继承到虚拟环境。 创建前可以先点existing看看有没有已经建好的虚拟环境 有的时候pycharm有问题,创建了虚拟环境没有显示。找一个.py文…...

Git企业开发控制理论和实操-从入门到深入(三)|分支管理
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...
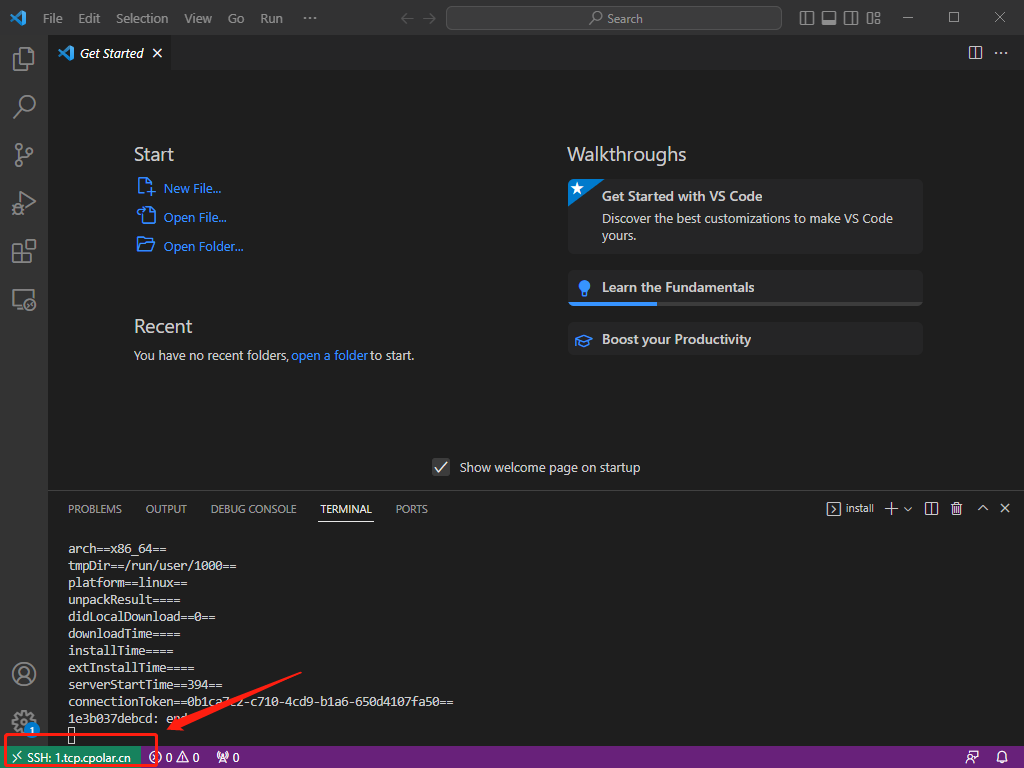
【VsCode】SSH远程连接Linux服务器开发,搭配cpolar内网穿透实现公网访问(1)
文章目录 前言1、安装OpenSSH2、vscode配置ssh3. 局域网测试连接远程服务器4. 公网远程连接4.1 ubuntu安装cpolar内网穿透4.2 创建隧道映射4.3 测试公网远程连接 5. 配置固定TCP端口地址5.1 保留一个固定TCP端口地址5.2 配置固定TCP端口地址5.3 测试固定公网地址远程 前言 远程…...
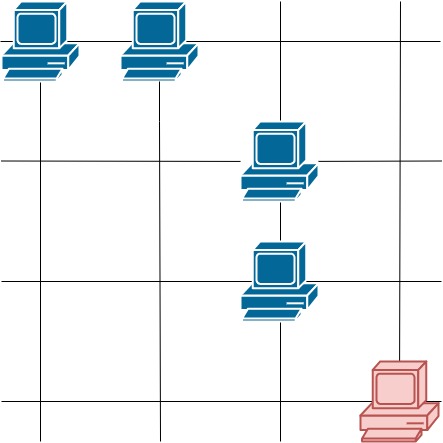
LC-1267. 统计参与通信的服务器(枚举 + 计数)
1267. 统计参与通信的服务器 中等 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。 请…...
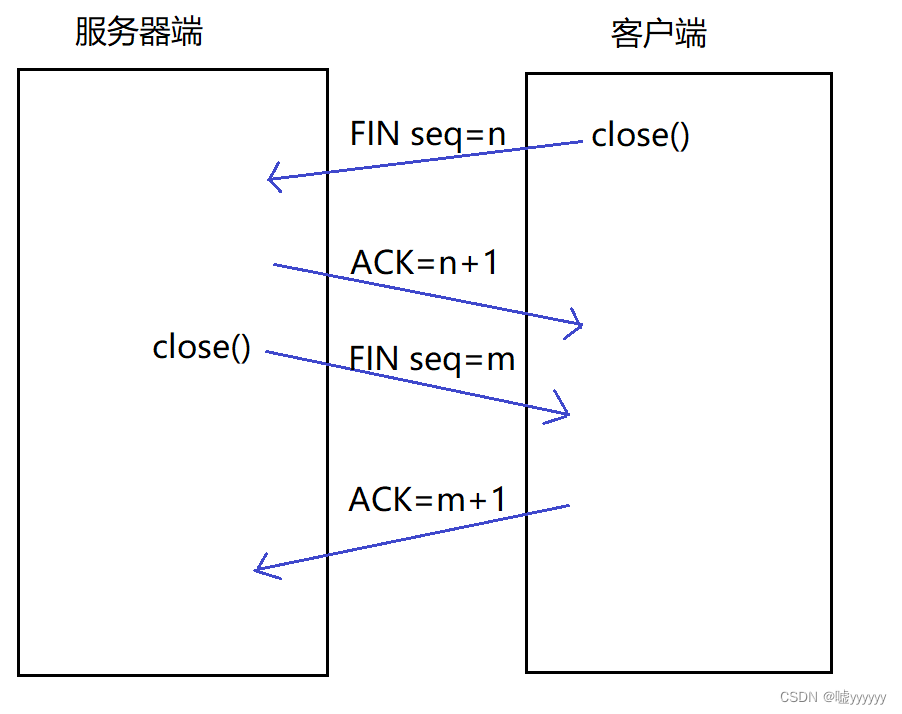
Linux TCP协议——三次握手,四次挥手
一、TCP协议介绍 TCP协议是可靠的、面向连接的、基于字节流的传输层通信协议。 TCP的头部结构: 源/目的端口号: 表示数据是从哪个进程来, 到哪个进程去;(tcp是传输层的协议,端与端之间的数据传输,在TCP和UDP协议当中不会体现出I…...
人机对抗智能-部分可观测异步智能体协同(POAC)
环境链接:数据中心-人机对抗智能 (ia.ac.cn)http://turingai.ia.ac.cn/data_center/show/10 1.环境配置 Ubuntu 20.04 Anaconda python版本3.6 1.1 安装torch0.4.1失败 参考文章: 安装torch0.4.1的神坑_torch0.4.1_DEMO_Tian的博客-CSDN博客 co…...
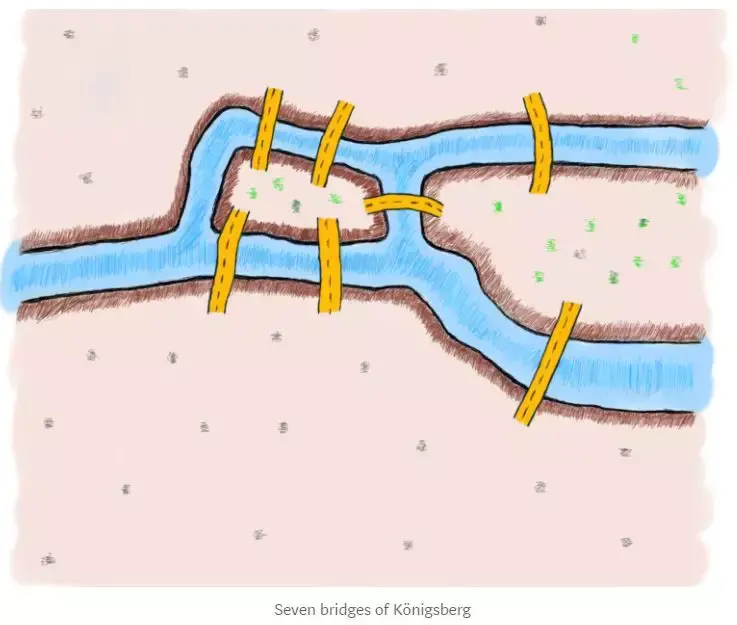
数学——七桥问题——图论
当涉及数学,有很多不同的话题可以讨论。你是否有特定的数学领域、概念或问题想要了解更多?以下是一些常见的数学领域和主题,你可以选择一个或者告诉我你感兴趣的具体内容,我将很乐意为你提供更多信息: 代数学ÿ…...

python 模块lxml 处理 XML 和 HTML 数据
xpath:https://blog.csdn.net/randy521520/article/details/132432903 一、安装 XPath (XML Path Language) 是一门在 HTML\XML 文档中查找信息的语言,可用来在 HTML\XML 文档中对元素和属性进行遍历。 pip install lxml二、使用案例 from lxml impo…...

SpringBoot 统⼀功能处理
统⼀功能处理 1. 拦截器2. 统⼀异常处理3. 统⼀数据返回格式 1. 拦截器 Spring 中提供了具体的实现拦截器:HandlerInterceptor,拦截器的实现分为以下两个步骤: 创建⾃定义拦截器,实现 HandlerInterceptor 接⼝的 preHandle&…...

hadoop 报错 java.io.IOException: Inconsistent checkpoint fields
背景: 使用了格式化,导致首重了新的集群ID org.apache.hadoop.hdfs.server.common.InconsistentFSStateException: Directory /work1/home/hadoop/dfs/data/current/BP-1873526852-172.16.21.30-1692769875005 is in an inconsistent state: namespaceID is incompatible with …...
workbench连接MySQL8.0错误 bad conversion 外部组件 异常
阿里云搭建MySQL实用的版本是8.0 本地安装的版本是: workbench 6.3 需要升级到: workbench 8.0 https://dev.mysql.com/downloads/workbench/...
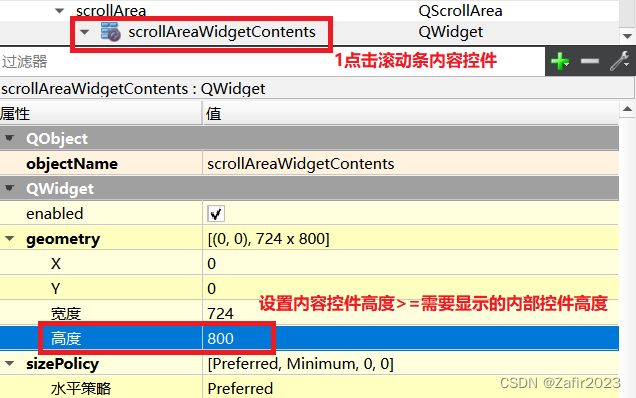
Qt Scroll Area控件设置,解决无法显示全部内容,且无法滚动显示问题。
前言,因为要显示很多条目的内容,原来是用Vertical Layout控件里面嵌套Horizontal layout显示了很多行控件,发现最简单的方法就是使用滚动条控件,但是无论如何调整需要滚动的控件高度,始终无法滚动显示内容。也就是说添…...
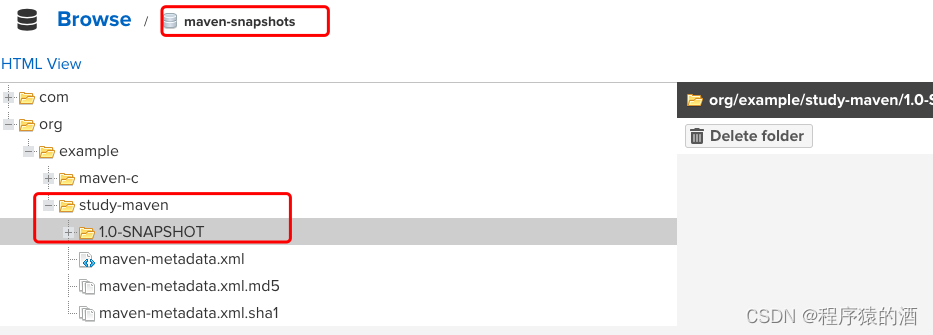
【Java架构-包管理工具】-Maven私服搭建-Nexus(三)
本文摘要 Maven作为Java后端使用频率非常高的一款依赖管理工具,在此咱们由浅入深,分三篇文章(Maven基础、Maven进阶、私服搭建)来深入学习Maven,此篇为开篇主要介绍Maven私服搭建-Nexus 文章目录 本文摘要1. Nexus安装…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
