数学——七桥问题——图论
当涉及数学,有很多不同的话题可以讨论。你是否有特定的数学领域、概念或问题想要了解更多?以下是一些常见的数学领域和主题,你可以选择一个或者告诉我你感兴趣的具体内容,我将很乐意为你提供更多信息:
-
代数学: 包括代数方程、多项式、群论、环论等。
-
几何学: 从欧几里得几何到非欧几何,涉及空间、形状、位置等。
-
微积分: 研究变化率和积分,是分析学的基础。
-
概率与统计: 研究随机事件的概率和数据的分析。
-
数论: 研究整数的性质,包括素数、同余、数的分解等。
-
线性代数: 研究向量、矩阵、线性方程组等。
-
微分方程: 研究包含导数的方程,用于建模自然现象。
-
数学逻辑与集合论: 探讨命题、证明、集合的性质等。
-
离散数学: 包括图论、组合数学、逻辑等离散结构的研究。
-
应用数学: 数学在科学、工程、经济等领域的应用。
-
数学史: 探索数学的历史、数学家的贡献等。
历史背景
七桥问题源自欧拉(Leonhard Euler)在18世纪的研究。他在1736年首次提出了这个问题,通过解决这一问题,他为图论领域的创立奠定了基础。欧拉是瑞士数学家,以其在多个数学分支上的贡献而闻名,而七桥问题是他在图论领域最具影响力的作品之一。
问题描述
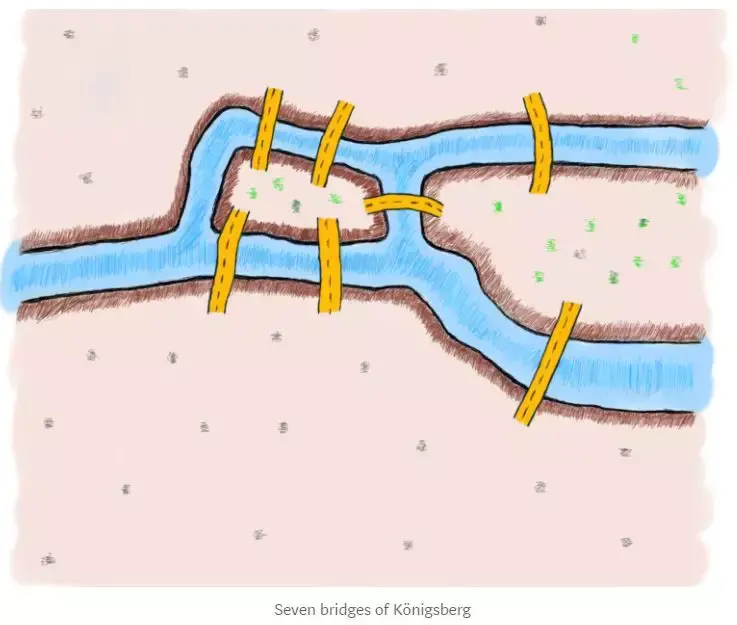
七桥问题的背景是庞特赫特里(现俄罗斯城市库尤比希夫)。这座城市由一座小岛和四个大陆组成,这些陆地和岛屿之间由七座桥连接。问题是,是否可能通过这些桥,恰好经过一次每座桥,将所有的陆地和岛屿连接起来,并且回到出发点,即起点。
解法与图论
欧拉通过抽象建模将七桥问题转化为图论问题,这是一种描述关系网络的数学方法。他将桥视为图中的边,陆地和岛屿视为图中的节点。这样,问题就变成了在图中找到一条路径,该路径通过每条边一次且仅一次,连接所有节点,并回到起点。
欧拉证明了,如果一个图中的节点的度数(连接边的数量)为奇数的节点数量是0或2,那么这个图可以有一个“欧拉路径”,即一条通过每条边一次且仅一次的路径。如果奇数度节点的数量超过2,那么没有欧拉路径。在七桥问题中,每个节点的度数都是奇数,因此无法找到满足条件的路径。
这一结论不仅解决了七桥问题,还奠定了图论领域的基础。欧拉路径和欧拉回路这些概念被广泛应用于电路设计、网络规划、交通优化等许多实际问题中。
影响与应用
七桥问题的解决对数学和其他领域产生了深远影响。首先,它标志着图论作为数学分支的诞生,图论成为了一种独立的数学领域,用于研究各种实际问题的抽象模型。其次,七桥问题展示了抽象建模和逻辑推理在解决复杂问题中的强大力量,这一思维方式在数学和科学研究中得到广泛应用。
此外,七桥问题也在教育领域有重要作用。它被广泛用作教学案例,帮助学生理解抽象数学概念和解决问题的方法。通过解决这个问题,学生能够培养逻辑思维、抽象建模和问题求解的能力。
总之,七桥问题不仅仅是数学史上的经典问题,更是一个启发性的故事,展示了数学思维如何在解决实际问题中发挥关键作用,以及如何为新的数学领域铺平道路。它在数学、教育和应用领域都具有重要意义。
当涉及图论时,我们在数学和计算机科学领域中遇到了一个有趣而重要的主题。图论研究的是图(Graph)这种抽象结构,它由节点(顶点)和连接节点的边组成。以下是一些图论的基本概念、应用和相关领域的介绍:
基本概念
-
图(Graph): 图是由一组节点和连接这些节点的边组成的抽象结构。图可以分为有向图和无向图,根据边是否有方向性。
-
顶点(Vertex): 图中的节点也被称为顶点,它们通常用来表示实体或对象。
-
边(Edge): 两个顶点之间的连接被称为边,边可以带有权重来表示节点间的关系强度。
-
度数(Degree): 对于无向图,一个顶点的度数是与它相连的边的数量。对于有向图,分为出度和入度,分别是从该顶点出发的边和指向该顶点的边的数量之和。
常见问题和概念
-
路径(Path): 顶点序列的一个序列,其中每个顶点通过一条边连接到下一个顶点。
-
环(Cycle): 至少包含三个顶点的路径,第一个和最后一个顶点相同,形成一个环。
-
连通性(Connectivity): 判断图中是否存在路径连接任意两个顶点。
-
最短路径(Shortest Path): 两个顶点之间的最短路径,可以通过各种算法找到,如迪杰斯特拉算法、弗洛伊德算法等。
应用领域
图论在许多领域都有广泛应用,包括但不限于:
-
网络分析: 用于分析社交网络、通信网络、互联网等的结构和关系。
-
交通规划: 优化道路、航班、列车线路等的设计和规划。
-
电路设计: 用于设计电子电路中的连接和布线。
-
排程问题: 解决任务分配、工作流程优化等问题。
-
生物学: 用于研究分子交互、蛋白质相互作用等。
-
优化问题: 在各种实际问题中,如资源分配、最优路径等。
相关领域
图论与许多其他数学和计算机科学领域紧密相关,包括:
-
组合数学: 图论中的许多问题涉及组合学的概念,如排列、组合等。
-
算法设计: 许多图论问题需要有效的算法来解决,如图的遍历、最短路径等。
-
计算机科学: 图数据结构在数据库、图数据库、编译器等领域有广泛应用。
相关文章:

数学——七桥问题——图论
当涉及数学,有很多不同的话题可以讨论。你是否有特定的数学领域、概念或问题想要了解更多?以下是一些常见的数学领域和主题,你可以选择一个或者告诉我你感兴趣的具体内容,我将很乐意为你提供更多信息: 代数学ÿ…...

python 模块lxml 处理 XML 和 HTML 数据
xpath:https://blog.csdn.net/randy521520/article/details/132432903 一、安装 XPath (XML Path Language) 是一门在 HTML\XML 文档中查找信息的语言,可用来在 HTML\XML 文档中对元素和属性进行遍历。 pip install lxml二、使用案例 from lxml impo…...

SpringBoot 统⼀功能处理
统⼀功能处理 1. 拦截器2. 统⼀异常处理3. 统⼀数据返回格式 1. 拦截器 Spring 中提供了具体的实现拦截器:HandlerInterceptor,拦截器的实现分为以下两个步骤: 创建⾃定义拦截器,实现 HandlerInterceptor 接⼝的 preHandle&…...

hadoop 报错 java.io.IOException: Inconsistent checkpoint fields
背景: 使用了格式化,导致首重了新的集群ID org.apache.hadoop.hdfs.server.common.InconsistentFSStateException: Directory /work1/home/hadoop/dfs/data/current/BP-1873526852-172.16.21.30-1692769875005 is in an inconsistent state: namespaceID is incompatible with …...
workbench连接MySQL8.0错误 bad conversion 外部组件 异常
阿里云搭建MySQL实用的版本是8.0 本地安装的版本是: workbench 6.3 需要升级到: workbench 8.0 https://dev.mysql.com/downloads/workbench/...
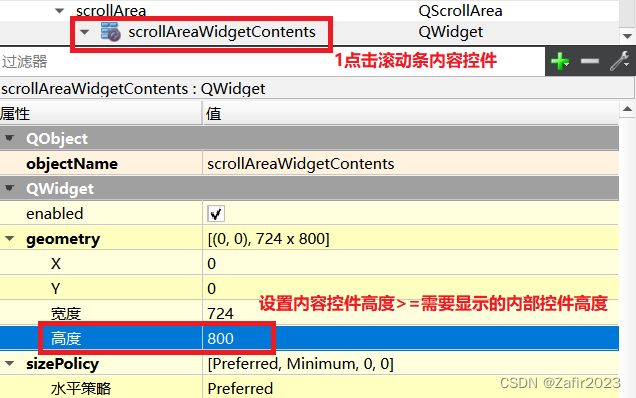
Qt Scroll Area控件设置,解决无法显示全部内容,且无法滚动显示问题。
前言,因为要显示很多条目的内容,原来是用Vertical Layout控件里面嵌套Horizontal layout显示了很多行控件,发现最简单的方法就是使用滚动条控件,但是无论如何调整需要滚动的控件高度,始终无法滚动显示内容。也就是说添…...
【Java架构-包管理工具】-Maven私服搭建-Nexus(三)
本文摘要 Maven作为Java后端使用频率非常高的一款依赖管理工具,在此咱们由浅入深,分三篇文章(Maven基础、Maven进阶、私服搭建)来深入学习Maven,此篇为开篇主要介绍Maven私服搭建-Nexus 文章目录 本文摘要1. Nexus安装…...

守护进程(精灵进程)
目录 前言 1.如何理解前台进程和后台进程 2.守护进程的概念 3.为什么会存在守护进程 4.如何实现守护进程 5.测试 总结 前言 今天我们要介绍的是关于守护进程如何实现,可能有小伙伴第一次听到守护进程这个概念,感觉很懵,知道进程的概念&…...
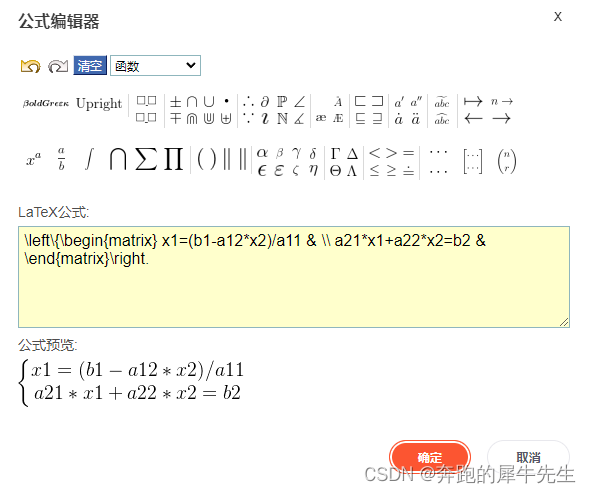
csdn冷知识:如何在csdn里输入公式或矩阵
目录 1 输入公式 2 输入矩阵 3 如何输入复杂公式 4 如何修改,已经生成的公式 1 输入公式 进入编辑模式点击右边的菜单:公式然后进入公式编辑器,选择右边的 ... 可以选择大括号等,右边还有矩阵符号选择后你需要创建几行几列的…...

【前端】CSS技巧与样式优化
目录 一、前言二、精灵图1、什么是精灵图2、为什么需要精灵图3、精灵图的使用①、创建CSS精灵图的步骤1)、选择合适的图标2)、合并图片3)、设置背景定位 ②、优化CSS精灵图的技巧1)、维护方便2)、考虑Retina屏幕3&…...
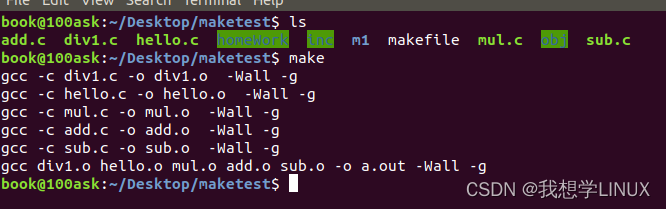
Linux下的系统编程——makefile入门
前言: 或许很多Winodws的程序员都不知道这个东西,因为那些Windows的IDE都为你做了这个工作,但我觉得要作一个好的和professional的程序员,makefile还是要懂。这就好像现在有这么多的HTML的编辑器,但如果你想成为一个专…...

redis常用五种数据类型详解
目录 前言: string 相关命令 内部编码 应用场景 hash 相关命令 内部编码 应用场景 list 相关命令 内部编码 应用场景 set 相关命令 内部编码 应用场景 Zset 相关命令 内部编码 应用场景 渐进式遍历 前言: redis有多种数据类型&…...

Python代理池健壮性测试 - 压力测试和异常处理
大家好!在构建一个可靠的Python代理池时,除了实现基本功能外,我们还需要进行一系列健壮性测试来确保其能够稳定运行,并具备应对各种异常情况的能力。本文将介绍如何使用压力测试工具以及合适的异常处理机制来提升Python代理池的可…...

回文子串-中心拓展
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不…...

2023.8各大浏览器11家对比:Edge/Chrome/Opera/Firefox/Tor/Vivaldi/Brave,安全性,速度,体积,内存占用
测试环境:全默认设置的情况下,均在全新的系统上进行测试,系统并未进行任何改动,没有杀毒软件,浏览器进程全部在后台,且为小窗模式,小窗分辨率均为浏览器厂商默认缩放大小(变量不唯一)࿰…...
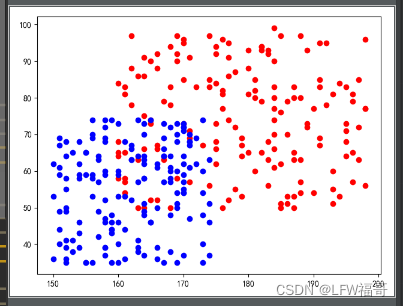
python中的matplotlib画散点图(数据分析与可视化)
python中的matplotlib画散点图(数据分析与可视化) import numpy as np import pandas as pd import matplotlib.pyplot as pltpd.set_option("max_columns",None) plt.rcParams[font.sans-serif][SimHei] plt.rcParams[axes.unicode_minus]Fa…...
2023前端面试笔记 —— HTML5
系列文章目录 内容链接2023前端面试笔记HTML5 文章目录 系列文章目录前言一、HTML 文件中的 DOCTYPE 是什么作用二、HTML、XML、XHTML 之间有什么区别三、前缀为 data- 开头的元素属性是什么四、谈谈你对 HTML 语义化的理解五、HTML5 对比 HTML4 有哪些不同之处六、meta 标签有…...

【LeetCode】面试题总结 消失的数字 最小k个数
1.消失的数字 两种思路 1.先升序排序,再遍历并且让后一项与前一项比较 2.转化为数学问题求等差数列前n项和 (n的大小为数组的长度),将根据公式求得的应有的和数与数组中实际的和作差 import java.util.*; class Solution {public …...
)
导入功能importExcel (现成直接用)
1. 实体类字段上加 Excel(name "xxx"), 表示要导入的字段 Excel(name "用户名称")private String nickName; 2. controller (post请求) /*** 导入用户数据** param file 文件* param updateSupport 是否更新支持,如果已存在,则进…...

cvc-complex-type.2.4.a: 发现了以元素 ‘base-extension‘ 开头的无效内容。应以 ‘{layoutlib}‘ 之一开头
不能飞的猪只是没用的猪。 —— 宫崎骏 《红猪》 常见的1种case 记录一下,新电脑安装android studio导入公司那些gradle还是5.5左右的工程以后,各种不适应。编译问题出现了。老电脑都是好好的。 cvc-complex-type.2.4.a: 发现了以元素 ‘base-extensi…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
