n-皇后问题(DFS)
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
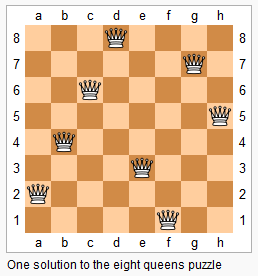
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..这题的难度就在于对于斜边的判定处理,解释放在代码里,这里直接给出代码
代码如下:
1.第一种方式(在看懂题意下可以知道每行只能放一个皇后,这样写代码更简单时间复杂度,推荐)
//第一种搜索方式
#include<iostream>
using namespace std;
const int N=20;
int n;
char g[N][N];
//由于国际象棋皇后的十字方向以及斜方向都能走,因此每行只能放一个皇后,定义一个行数组xiaochou,正斜线xie,反斜线fxie
bool xiaochou[N],xie[N],fxie[N];void dfs(int u)//u表示遍历到数组第u行
{if(u==n)//当遍历到第n-1行时已经进行完成,等于n直接输出{for(int i=0;i<u;i++) puts(g[i]);puts("");return;}for(int i=0;i<n;i++){if(!xiaochou[i]&&!xie[u+i]&&!fxie[n-u+i])//这里运用到一个数学知识,正对角线该点为u+i,其交叉对于的反对角线为n-u+i{g[u][i]='Q';xiaochou[i]=xie[u+i]=fxie[n-u+i]=true;dfs(u+1);xiaochou[i]=xie[u+i]=fxie[n-u+i]=false;//记得回溯g[u][i]='.';}}
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++) g[i][j]='.';}dfs(0);return 0;
}2.第二种方式(一个格子一个格子去枚举判断,比较容易理解,但时间复杂度要大一点)
#include<iostream>
using namespace std;
const int N=20;
int n;
char g[N][N];
//由于国际象棋皇后的十字方向以及斜方向都能走,第二种方法就是把每个格子都枚举一遍
//设置row行数组,col列数组以及两个对角线数组,来判断皇后能不能放
bool row[N],col[N],xie[N],fxie[N];void dfs(int x,int y,int s)//x和y分别表示枚举该数组到啥位置的行列坐标,s表示已经放了几个皇后
{if(y==n) y=0,x++;//每行列举完最后一列的时候,跳到下一行的第一列if(x==n){if(s==n){for(int i=0;i<n;i++) puts(g[i]);puts("");}return;}//不放皇后dfs(x,y+1,s);//放皇后if(!row[x]&&!col[y]&&!xie[x+y]&&!fxie[x-y+n]){g[x][y]='Q';row[x]=col[y]=xie[x+y]=fxie[x-y+n]=true;dfs(x,y+1,s+1);row[x]=col[y]=xie[x+y]=fxie[x-y+n]=false;g[x][y]='.';}
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++) g[i][j]='.';}dfs(0,0,0);return 0;
}
难点总结:
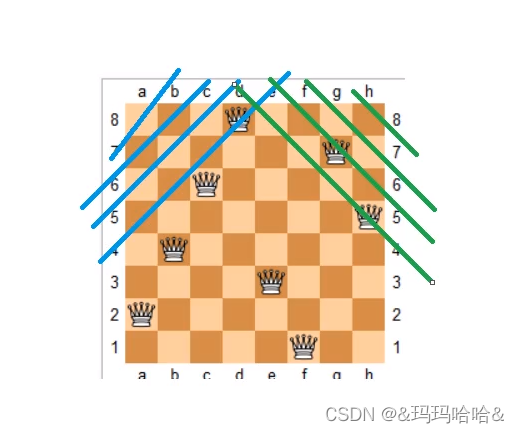
这题需要补充的知识点就是关于对角线如何处理的问题,这里设置正对角线数组和反对角线数组来处理,正对角线为蓝色下标从左上角开始,反对角线为绿色下标从右上角开始,这里因为只要对角线中有一个皇后剩下的都不能放,所以可以看成一个bool类型的一维数组,而难处也在于bool数组的下标应该如何设置,
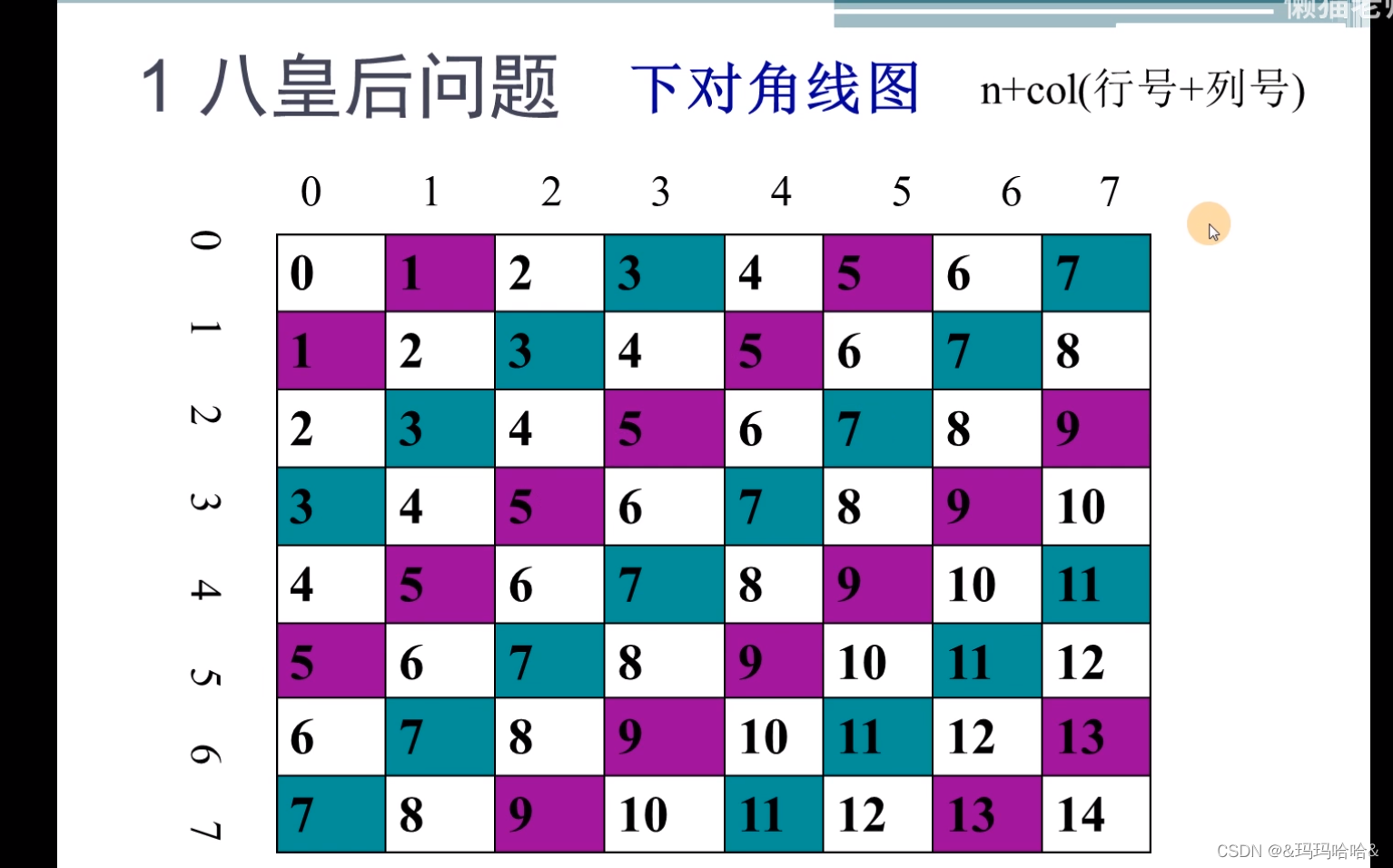
对于正对角线(如下图),规律就是其对角线格子横坐标加上纵坐标相等,因此代码中为x+y,
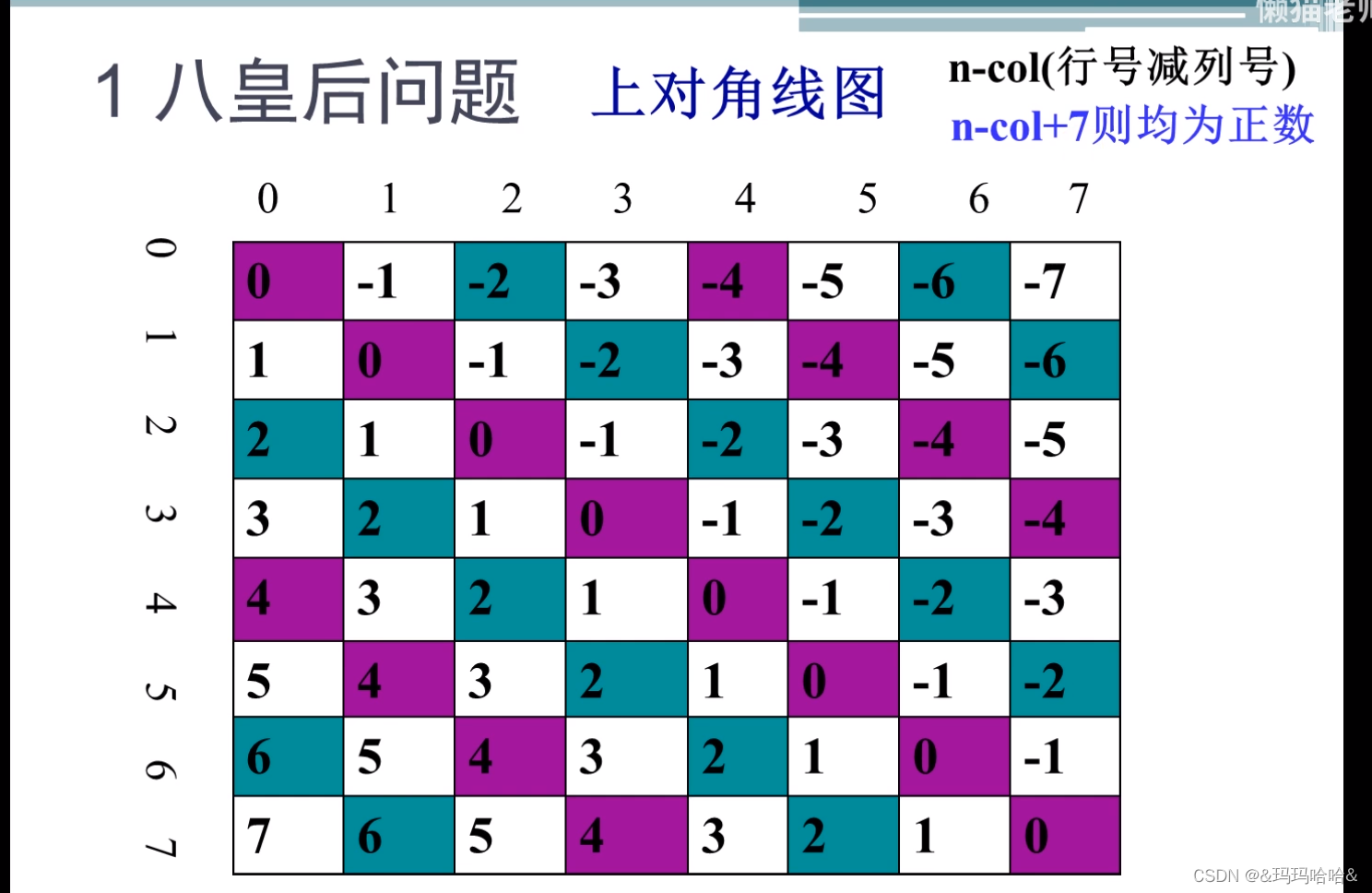
对于反对角线,为x-y+n,这里加n是为了不出现负数
相关文章:

n-皇后问题(DFS)
n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 输入格式 共一行,包含整数 n。 输出…...

漏洞利用和权限提升
使用Kali Linux进行漏洞利用和权限提升是渗透测试过程中的一部分,用于评估系统的安全性。 漏洞利用: 选择目标: 首先,确定 要进行漏洞利用的目标系统。这可能是一个具有已知漏洞的应用程序、服务或操作系统。 收集信息ÿ…...

开源网安受邀参加软件供应链安全沙龙,推动企业提升安全治理能力
8月23日下午,合肥软件行业软件供应链安全沙龙在中安创谷科技园举办。此次沙龙由合肥软件产业公共服务中心联合中安创谷科技园公司共同主办,开源网安软件供应链安全专家王晓龙、尹杰受邀参会并带来软件供应链安全方面的精彩内容分享,共同探讨…...

回归分析扫盲:为什么非线性模型不能直接用最优子集选择法
最近有人给我发了篇文章: 一个问题有一堆变量,我们要选取哪些变量来建模呢?我们来看看这篇文章是怎么做的: 这个方法简单来说就是:对于这一堆变量,我们每次尝试剔除其中一个变量,然后用剩下的变…...

单例模式简介
概念: 单例模式(Singleton Pattern)是一种创建型设计模式,它确保一个类只有一个实例,并提供全局访问点。单例模式的核心思想是限制某个类只能创建一个对象实例,并提供对该实例的全局访问。这样可以避免多个…...
WPF自定义命令及属性改变处理
1、项目建构 2、自定义命令 namespace WpfDemo.Base {public class MyCommand : ICommand{Action executeAction;public MyCommand(Action action){executeAction action;}public event EventHandler? CanExecuteChanged;public bool CanExecute(object? parameter){retu…...

macbook m1 docker中使用go
已经有一个centos8的镜像,本来打算在centos8中安装go 安装方法: # 1.下载go的安装包 mkdir install && cd install # 任意创建个文件夹 wget https://go.dev/dl/go1.20.2.linux-amd64.tar.gz# 2. 解压 tar -C xzf go1.20.2.linux-amd64.tar.g…...
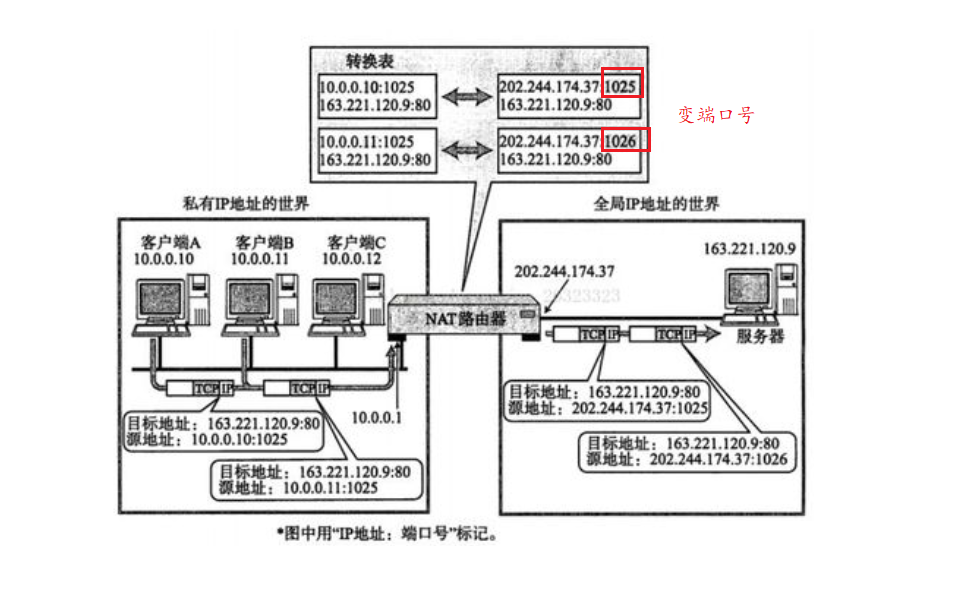
【Hello Network】DNS协议 NAT技术 代理服务器
本篇博客简介:介绍DNS协议 NAT技术和代理服务器 网络各协议补充 DNSDNS背景DNS介绍DNS总结域名简介 NAT技术NAT技术背景NAT IP转换过程NAPTNAT技术缺陷NAT和代理服务器 网络协议总结应用层传输层网络层数据链路层 DNS DNS是一整套从域名映射到IP的系统 DNS背景 为…...
Android 使用模拟器模拟Linux操作系统
1. 简介 在Android手机上使用模拟器模拟ubuntu等操作系统,便于测试 2. 软件准备 Termux:是一款 Android 终端模拟器和 Linux 环境应用程序,无需 root 或设置即可直接运行。虽然酷安和谷歌菜市场都能下载,但这些渠道都很久没更新…...

机器学习基础之《分类算法(5)—朴素贝叶斯算法原理》
一、朴素贝叶斯算法 1、什么是朴素贝叶斯分类方法 之前用KNN算法,分类完直接有个结果,但是朴素贝叶斯分完之后会出现一些概率值,比如: 这六个类别,它都有一定的可能性 再比如,对文章进行分类:…...

# Go学习-Day6
文章目录 Go学习-Day6封装继承接口 Go学习-Day6 个人博客:CSDN博客 封装 类似java的类的封装,这里我们利用大小写和工厂模式来实现封装的功能略过 继承 相似的类具有相似的方法,反复绑定相同的方法,代码冗余,所以引…...
分布式 - 服务器Nginx:一小时入门系列之 HTTPS协议配置
文章目录 1. HTTPS 协议2. 生成 SSL 证书和私钥文件3. 配置 SSL 证书和私钥文件4. HTTPS 协议优化 1. HTTPS 协议 HTTPS 是一种通过计算机网络进行安全通信的协议。它是HTTP的安全版本,通过使用 SSL 或 TLS 协议来加密和保护数据传输。HTTPS的主要目的是确保在客户…...

探秘Linux系统性能监控神器!Linux和Python技术持续学习者必看!
引言 作为Linux运维工程师,我们经常需要对服务器的性能进行监控和调优。而Python作为一门强大的脚本语言,可以帮助我们轻松实现各种系统性能监控任务。本文将介绍几个实用的Python库和工具,帮助我们监控Linux系统的CPU、内存、磁盘和网络等性…...

文心一言续写太监小说《名侦探世界的巫师》
《名侦探世界的巫师》是我的童年回忆,总是想着续写一下,但是又没有时间和文笔,文心一言出了,由于目前大模型貌似可以联网,可以尝试搞一波~ 目录 文章1【前六个故事还能看,后面就是在重复】故事2【辣眼睛】…...
)
Solidity 合约安全,常见漏洞(第三篇)
Solidity 合约安全,常见漏洞(第三篇) ERC20 代币问题 如果你只处理受信任的 ERC20 代币,这些问题大多不适用。然而,当与任意的或部分不受信任的 ERC20 代币交互时,就有一些需要注意的地方。 ERC20&#…...
Linux安装Redis数据库,无需公网IP实现远程连接
文章目录 1. Linux(centos8)安装redis数据库2. 配置redis数据库3. 内网穿透3.1 安装cpolar内网穿透3.2 创建隧道映射本地端口 4. 配置固定TCP端口地址4.1 保留一个固定tcp地址4.2 配置固定TCP地址4.3 使用固定的tcp地址连接 Redis作为一款高速缓存的key value键值对的数据库,在…...

智慧政务,长远布局——AIGC引领,加速推进数字化政府建设
在人工智能、虚拟现实等领域迅猛发展且日益成熟的背景下,AI行业正迈向蓬勃发展的全新阶段,市场规模持续扩张。与此同时,数字服务也正在蓬勃兴起,新一代信息技术为数字政府构建了坚实支撑,重塑了政务信息化管理、业务架…...
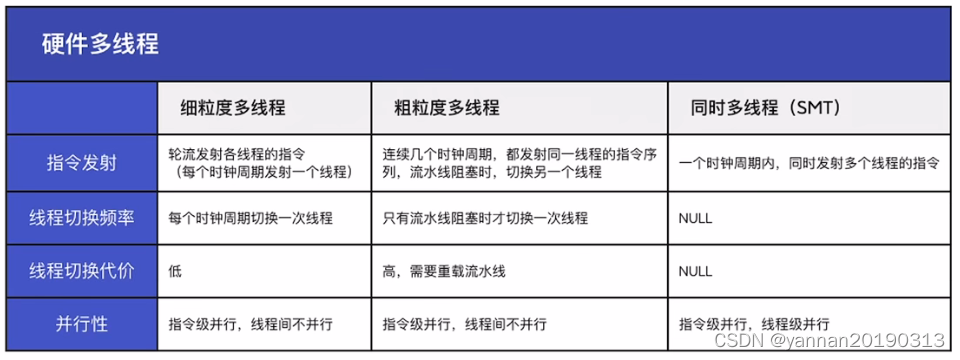
中央处理器(CPU):组成、指令周期、数据通路、控制方式、控制器、指令流水线,补充(多处理器系统、硬件多线程)
中央处理器(CPU,Central Processing Unit),计算机控制和运算的核心,是信息处理和程序运行的执行单元。 CPU主要功能:处理指令、执行操作、控制时间、处理中断、处理数据。 其中,处理指令、执行…...

开源微服务如何选型?Spring Cloud、Dubbo、gRPC、Istio 详细对比
作者:刘军 不论您是一名开发者、架构师、CTO, 如果您曾深度参与在微服务开发中,那么相信您一定有过开源微服务框架或体系选型的疑问:Apache Dubbo、Spring Cloud、gRPC 以及 Service Mesh 体系产品如 Istio,到底应该选…...

Nginx的HTTPS部署与安全性能优化
Nginx作为一款高性能的Web服务器和反向代理服务器,被广泛用于应用部署和负载均衡。在安全环保意识的逐渐提高下,HTTPS也成为现代Web应用中必不可少的一环。本篇文章将重点介绍Nginx的HTTPS部署和安全性能优化。 一、Nginx的HTTPS部署 证书申请 首先需要去…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
