算法leetcode|73. 矩阵置零(rust重拳出击)
文章目录
- 73. 矩阵置零:
- 样例 1:
- 样例 2:
- 提示:
- 进阶:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
73. 矩阵置零:
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
样例 1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]输出:[[1,0,1],[0,0,0],[1,0,1]]
样例 2:

输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
- m == matrix.length
- n == matrix[0].length
- 1 <= m, n <= 200
- -231 <= matrix[i][j] <= 231 - 1
进阶:
- 一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
- 一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
- 你能想出一个仅使用常量空间的解决方案吗?
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 要遍历整个矩阵是肯定的了,所以时间复杂度上似乎没什么大的技巧,重点在空间复杂度上。
- 不使用额外空间,直接在遍历中就将行和列置0,会导致还没有遍历到的值丢失。
- 可以将原矩阵整体拷贝一份作为备份,然后遍历这个备份的矩阵,去直接将原矩阵置0,这样会使用 O(mn) 的额外空间。
- 一个简单的改进方案是使用两个额外的数组,存储每一行是否出现过0,和每一列是否出现过0,然后再利用这两个额外的标记数组将原矩阵置0,这样会使用 O(m + n) 的额外空间。
- 可以进一步优化,我们可以用矩阵的第一行和第一列代作为标记数组。但这样会导致原数组的第一行和第一列被修改,无法记录它们是否原本包含 0。因此我们需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0,这样仅仅需要 O(1) 的额外空间。
题解:
rust:
impl Solution {pub fn set_zeroes(matrix: &mut Vec<Vec<i32>>) {let (m, n) = (matrix.len(), matrix[0].len());let (mut flag_row0, mut flag_col0) = (false, false);// 第一行是否有0for i in 0..n {if matrix[0][i] == 0 {flag_row0 = true;break;}}// 第一列是否有0for i in 0..m {if matrix[i][0] == 0 {flag_col0 = true;break;}}// 标记(1..m).for_each(|i| {(1..n).for_each(|j| {if matrix[i][j] == 0 {matrix[i][0] = 0;matrix[0][j] = 0;}});});// 置0(1..m).for_each(|i| {(1..n).for_each(|j| {if matrix[i][0] == 0 || matrix[0][j] == 0 {matrix[i][j] = 0;}});});// 第一行置0if flag_row0 {for i in 0..n {matrix[0][i] = 0;}}// 第一列置0if flag_col0 {for i in 0..m {matrix[i][0] = 0;}}}
}
go:
func setZeroes(matrix [][]int) {m, n := len(matrix), len(matrix[0])row0, col0 := false, false// 第一行是否有0for _, v := range matrix[0] {if v == 0 {row0 = truebreak}}// 第一列是否有0for _, r := range matrix {if r[0] == 0 {col0 = truebreak}}// 标记for i := 1; i < m; i++ {for j := 1; j < n; j++ {if matrix[i][j] == 0 {matrix[i][0] = 0matrix[0][j] = 0}}}// 置0for i := 1; i < m; i++ {for j := 1; j < n; j++ {if matrix[i][0] == 0 || matrix[0][j] == 0 {matrix[i][j] = 0}}}// 第一行置0if row0 {for i := 0; i < n; i++ {matrix[0][i] = 0}}// 第一列置0if col0 {for _, r := range matrix {r[0] = 0}}
}
c++:
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {const int m = matrix.size(), n = matrix[0].size();bool flag_row0 = false, flag_col0 = false;// 第一行是否有0for (int i = 0; i < n; ++i) {if (!matrix[0][i]) {flag_row0 = true;break;}}// 第一列是否有0for (int i = 0; i < m; ++i) {if (!matrix[i][0]) {flag_col0 = true;break;}}// 标记for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {if (!matrix[i][j]) {matrix[i][0] = matrix[0][j] = 0;}}}// 置0for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {if (!matrix[i][0] || !matrix[0][j]) {matrix[i][j] = 0;}}}// 第一行置0if (flag_row0) {for (int i = 0; i < n; ++i) {matrix[0][i] = 0;}}// 第一列置0if (flag_col0) {for (int i = 0; i < m; ++i) {matrix[i][0] = 0;}}}
};
python:
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""m, n = len(matrix), len(matrix[0])# 第一行是否有0flag_row0 = any(matrix[0][i] == 0 for i in range(n))# 第一列是否有0flag_col0 = any(matrix[i][0] == 0 for i in range(m))# 标记for i in range(1, m):for j in range(1, n):if matrix[i][j] == 0:matrix[i][0] = matrix[0][j] = 0# 置0for i in range(1, m):for j in range(1, n):if matrix[i][0] == 0 or matrix[0][j] == 0:matrix[i][j] = 0# 第一行置0if flag_row0:for j in range(n):matrix[0][j] = 0# 第一列置0if flag_col0:for i in range(m):matrix[i][0] = 0java:
class Solution {public void setZeroes(int[][] matrix) {final int m = matrix.length, n = matrix[0].length;boolean flagRow0 = false, flagCol0 = false;// 第一行是否有0for (int i = 0; i < m; ++i) {if (matrix[i][0] == 0) {flagCol0 = true;break;}}// 第一列是否有0for (int i = 0; i < n; ++i) {if (matrix[0][i] == 0) {flagRow0 = true;break;}}// 标记for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {if (matrix[i][j] == 0) {matrix[i][0] = matrix[0][j] = 0;}}}// 置0for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {if (matrix[i][0] == 0 || matrix[0][j] == 0) {matrix[i][j] = 0;}}}// 第一行置0if (flagRow0) {for (int i = 0; i < n; ++i) {matrix[0][i] = 0;}}// 第一列置0if (flagCol0) {for (int i = 0; i < m; ++i) {matrix[i][0] = 0;}}}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
相关文章:

算法leetcode|73. 矩阵置零(rust重拳出击)
文章目录 73. 矩阵置零:样例 1:样例 2:提示:进阶: 分析:题解:rust:go:c:python:java: 73. 矩阵置零: 给定一个 m x n 的矩…...

axios 二次封装
axios 二次封装 基本上每一个项目开发,都必须要二次封装 axios。主要是为了减少重复性工作,不可能每一次发起新请求时,都要重新配置请求域名、请求头 Content-Type、Token 等信息。所以需要把公用的部分都封装成一个函数,每次调用…...

Rust安全之数值
文章目录 数值溢出 数值溢出 编译通过,运行失败 cargo run 1 fn main() {let mut arg std::env::args().skip(1).map(|x| x.parse::<i32>().unwrap()).next().unwrap();let m_i i32::MAX - 1;let a m_i arg;println!("{:?}", a); }thread main panicked…...

4种方法实现html 页面内锚点定位及跳转
使用scrollIntoView进行锚点定位效果 不知道你有没有遇到这样的需求:锚点定位?进入页面某个元素需要出现在可视区?…这一类的需求归根结底就是处理元素与可视区域的关系。我接触了很多前端小伙伴,实现的方式有各种各样的ÿ…...

gitlab配置备忘
版本 gitlab 14.6.2 gitlab备份上传到阿里云oss ### Backup Settings ###! Docs: https://docs.gitlab.com/omnibus/settings/backups.html# gitlab_rails[manage_backup_path] true # gitlab_rails[backup_path] "/var/opt/gitlab/backups"###! Docs: https://…...

基于Centos搭建k8s仓库
系统环境: Red Hat Enterprise Linux 9.1 (Plow) Kernel: Linux 5.14.0-162.6.1.el9_1.x86_64 主机名地址master192.168.19.128node01192.168.19.129node02192.168.19.130 目录 1、关闭防火墙,关闭SElinxu ,开启时间同步服务 2、关…...
浅谈泛在电力物联网发展形态与技术挑战
安科瑞 华楠 摘 要:泛在电力物联网是当前智能电网发展的一个方向。首先,总结了泛在电力物联网的主要作用和价值体现;其次,从智能电网各个环节概述了物联网技术在电力领域的已有研究和应用基础;进而,构思并…...

git reset --soft 用法
git reset --soft 是 Git 命令中的一个选项,它用于取消之前的提交,并将取消的更改保留在暂存区。这允许您重新组织提交历史或将更改合并到一个新的提交中,而不影响暂存区和工作目录中的更改。 这个命令的语法是: git reset --so…...

哪些测试仪器可以用于检测静电中和设备的性能
静电设备性能测试通常需要使用一些专门的仪器来进行。以下是一些常见的静电设备性能测试仪器: 1. 静电电压测试仪:用于测量物体表面的静电电压。它通常可以测量正负电压,并具有高精度和快速响应的特点。 2. 静电电荷仪:用于测量物…...

浅析 GlusterFS 与 JuiceFS 的架构异同
在进行分布式文件存储解决方案的选型时,GlusterFS 无疑是一个不可忽视的考虑对象。作为一款开源的软件定义分布式存储解决方案,GlusterFS 能够在单个集群中支持高达 PiB 级别的数据存储。自从首次发布以来,已经有超过十年的发展历程。目前&am…...
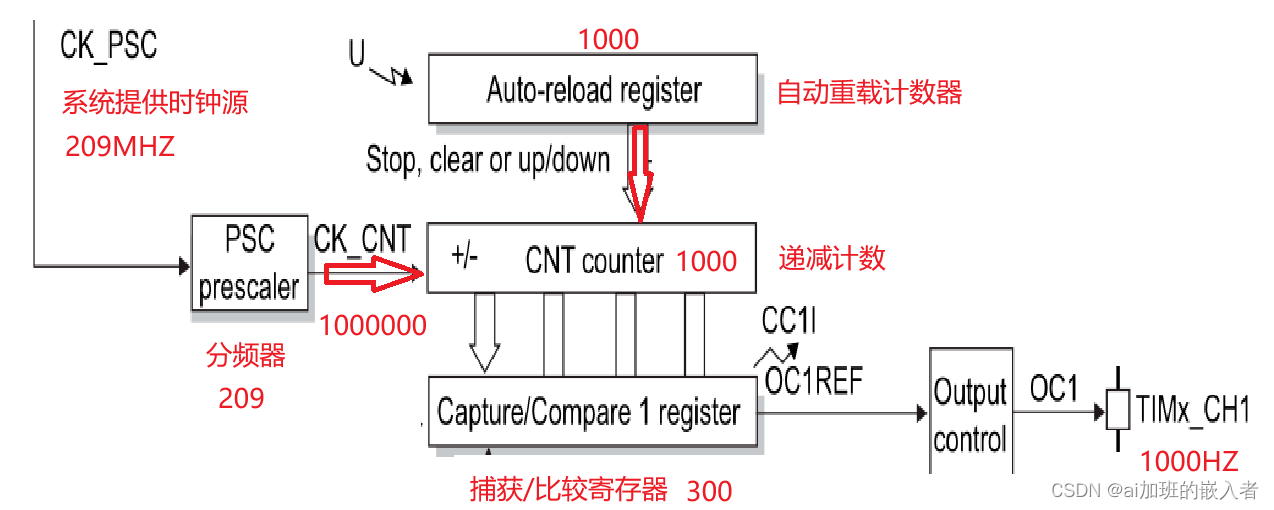
ARM开发,stm32mp157a-A7核PWM实验(驱动蜂鸣器,风扇,马达工作)
1.分析框图; 2.比较捕获寄存器(产生PWM方波); 工作原理: 1、系统提供一个时钟源209MHZ,需要通过分频器进行分频,设置分频器值为209分频; 2、当定时器启动之后,自动重载…...
|消费者需求研究方案)
群狼调研(长沙眼镜店神秘顾客)|消费者需求研究方案
本文由群狼调研(长沙品牌调研)出品,欢迎转载,请注明出处。消费者需求研究方案是在开展研究之前制定的计划,用于指导研究的设计、实施和分析。以下是一个可能的消费者需求研究方案的大致框架: 1. 研究目标和问题: • …...

电脑入门:宽带路由器常见故障排除技巧
宽带路由器在企业网络中的应用是相当广泛的,在运行的过程中出现故障是在所难免的,虽然故障现象多种多样,引起故障发生的原因也不尽相同,但从大体上可以把这些故障分为硬件故障和软件故障,具体来说就是一些网络连接性问题、配置文件选项问题以及网络协议问题等。 由于路由器…...

基于云原生网关的流量防护实践
作者:涂鸦 背景 在分布式系统架构中,每个请求都会经过很多层处理,比如从入口网关再到 Web Server 再到服务之间的调用,再到服务访问缓存或 DB 等存储。在下图流量防护体系中,我们通常遵循流量漏斗原则进行流量防护。…...

开源与云计算:新的合作模式
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
前端需要理解的跨平台知识
混合开发是指使用多种开发模开发App的一种开发模式,涉及到两大类技术:原生 Native、Web H5。原生 Native 主要指 iOS(Objective C)、Android(Java),原生开发效率较低,开发完成需要重…...

《基于 Vue 组件库 的 Webpack5 配置》3.将 CSS 提取到单独的文件
使用 webpack 插件 mini-css-extract-plugin 需要额外安装 npm i mini-css-extract-pluginlatest -D; 同时打包 js 和 css 文件时,可参考 entry 高级用法; package.json 的配置如下 const { VueLoaderPlugin } require(vue-loader); // 可…...

2023CCF图形学启明星计划夏令营感想记录
这篇就是纯日记了,想记录一下参加这个夏令营的感想,中间的一些过程,毕竟这对我来说算是一段难忘的经历。 一、了解到的渠道 我个人是比较喜欢图形渲染的,之前也学过GAMES的课程,然后偶然的一天,GAMES101里…...

如何解决“缺失msvcp110.dll”错误,msvcp110.dll丢失要怎样才能修复
今天,我将为大家分享关于电脑提示msvcp110.dll丢失的3种修复方法。希望这些方法能帮助到正在遇到这个问题的朋友们。 首先,我们来了解一下msvcp110.dll文件的作用。msvcp110.dll是Microsoft Visual C 2010 Redistributable Package的一部分,…...

激活函数总结(二十):激活函数补充(SQNL、PLU)
激活函数总结(二十):激活函数补充 1 引言2 激活函数2.1 Square nonlinearity (SQNL)激活函数2.2 Piecewise Linear Unit (PLU)激活函数 3. 总结 1 引言 在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PR…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
