2022年03月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试

第1题:拦截导弹
某国为了防御敌国的导弹袭击, 发展出一种导弹拦截系统。 但是这种导弹拦截系统有一个缺陷: 虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。 某天, 雷达捕捉到敌国的导弹来袭。 由于该系统还在试用阶段, 所以只有一套系统, 因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于 30000 的正整数) , 计算这套系统最多能拦截多少导弹。
时间限制: 1000
内存限制: 65536
输入
第一行是一个整数 N(不超过 15) , 表示导弹数。 第二行包含 N 个整数, 为导弹依次飞来的高度(雷达给出的高度数据是不大于 30000的正整数) 。
输出
一个整数, 表示最多能拦截的导弹数。
样例输入
8
389 207 155 300 299 170 158 65
样例输出
6
要解决拦截导弹的问题,可以使用动态规划的方法。
以下是使用C语言实现的代码:
#include <stdio.h>#define MAX_MISSILES 15int max(int a, int b) {return (a > b) ? a : b;
}int missileInterception(int missiles[], int n) {int dp[MAX_MISSILES] = {0};int maxInterceptions = 0;for (int i = 0; i < n; i++) {dp[i] = 1;for (int j = 0; j < i; j++) {if (missiles[i] <= missiles[j]) {dp[i] = max(dp[i], dp[j] + 1);}}maxInterceptions = max(maxInterceptions, dp[i]);}return maxInterceptions;
}int main() {int n;scanf("%d", &n);int missiles[MAX_MISSILES];for (int i = 0; i < n; i++) {scanf("%d", &missiles[i]);}int maxInterceptions = missileInterception(missiles, n);printf("%d\n", maxInterceptions);return 0;
}
该代码使用一个一维数组dp来保存状态,其中dp[i]表示以第i个导弹为结尾的最大拦截导弹数。
首先,初始化dp数组的所有元素为1,表示每个导弹都可以单独拦截。然后,遍历导弹数组,对于每个导弹missiles[i],在之前的导弹中查找高度小于等于当前导弹的导弹missiles[j],如果找到,则更新dp[i]为dp[j]+1,表示以导弹missiles[i]结尾的最大拦截导弹数。最后,找到dp数组中的最大值即为所求的最多能拦截的导弹数。
第2题:神奇的数列
一个正整数数列, 可以将它切割成若干个数据段, 每个数据段由值相同的相邻元素构成。 该数列的神奇之处在于, 每次切除一个数据段后,该数据段前后的元素自动连接在一起成为邻居。 例如从数列“2 8 9 77 6 9 4” 中切除数据段“7 7 ” 后, 余下的元素会构成数列“2 8 9 6 94”
请问若要将该数列切割成若干个数据段, 则至少会切出来几个数据段?
样例: 按下列顺序切割数列“2 8 9 7 7 6 9 4” , 只要切割成 6 段
切割出“7 7” , 余下 “2 8 9 6 9 4”
切割出 “6” , 余下 “2 8 9 9 4”
切割出 “9 9” , 余下 “2 8 4”
切割出 “2” , 余下 “8 4”
切割出 “8” , 余下 “4”
时间限制: 1000
内存限制: 65536
输入
第一行是一个整数, 示共有多少组测试数据。 每组测试数据的输入包括两行: 第一行是整数 N, N<=200,表示数列的长度, 第二行是 N 个正整数。
输出
每个测试案例的输出占一行, 是一个整数。 格式是: Case n: x n 是测试数据组编号, x 是答案
样例输入
2
8
2 8 9 7 7 6 9 4
16
2 8 9 7 7 6 9 4 4 2 8 4 2 7 6 9
样例输出
Case 1: 6
Case 2: 11
要解决神奇的数列问题,可以使用贪心算法。
以下是使用C语言实现的代码:
#include <stdio.h>#define MAX_LENGTH 200int min(int a, int b) {return (a < b) ? a : b;
}int countSegments(int sequence[], int n) {int segments = 1;for (int i = 1; i < n; i++) {if (sequence[i] != sequence[i - 1]) {segments++;}}return segments;
}int main() {int t;scanf("%d", &t);for (int i = 1; i <= t; i++) {int n;scanf("%d", &n);int sequence[MAX_LENGTH];for (int j = 0; j < n; j++) {scanf("%d", &sequence[j]);}int segments = countSegments(sequence, n);printf("Case %d: %d\n", i, segments);}return 0;
}
该代码使用一个循环遍历数列,对于每个数列元素sequence[i],如果它与前一个元素sequence[i-1]不相等,则将段数segments加1。最后,segments的值即为所求的切割数据段的数量。
第3题:硬币
宇航员 Bob 有一天来到火星上, 他有收集硬币的习惯。 于是他将火星上所有面值的硬币都收集起来了, 一共有 n 种, 每种只有一个: 面值分别为 a1,a2… an。 Bob 在机场看到了一个特别喜欢的礼物, 想买来送给朋友 Alice, 这个礼物的价格是 X 元。 Bob 很想知道为了买这个礼物他的哪些硬币是必须被使用的, 即 Bob 必须放弃收集好的哪些硬币种类。 飞机场不提供找零, 只接受恰好 X 元。
时间限制: 1000
内存限制: 262144
输入
第一行包含两个正整数 n 和 x。 (1 <= n <= 200, 1 <= x <= 10000) 第二行从小到大为 n 个正整数 a1, a2, a3 … an (1 <= ai <= 10000)
输出
第一行是一个整数, 即有多少种硬币是必须被使用的。 第二行是这些必须使用的硬币的面值(从小到大排列) 。
样例输入
5 18
1 2 3 5 10
样例输出
2
5 10
提示
输入数据将保证给定面值的硬币中至少有一种组合能恰好能够支付 X元。 如果不存在必须被使用的硬币, 则第一行输出 0, 第二行输出空行。
要解决硬币问题,可以使用动态规划的方法。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <stdbool.h>#define MAX_COINS 200
#define MAX_AMOUNT 10000bool dp[MAX_AMOUNT + 1] = {false};void findCoins(int coins[], int n, int amount) {dp[0] = true;for (int i = 0; i < n; i++) {for (int j = amount; j >= coins[i]; j--) {if (dp[j - coins[i]]) {dp[j] = true;}}}
}int main() {int n, amount;scanf("%d %d", &n, &amount);int coins[MAX_COINS];for (int i = 0; i < n; i++) {scanf("%d", &coins[i]);}findCoins(coins, n, amount);int count = 0;for (int i = 1; i <= amount; i++) {if (dp[i]) {count++;}}printf("%d\n", count);for (int i = 1; i <= amount; i++) {if (dp[i]) {printf("%d ", i);}}printf("\n");return 0;
}
该代码使用一个布尔数组dp来保存状态,其中dp[i]表示是否存在一种硬币组合,可以凑出金额i。
首先,将dp[0]设置为true,表示金额为0时不需要使用任何硬币。然后,遍历硬币数组coins,对于每个硬币coins[i],从amount向前遍历到coins[i],如果存在一种硬币组合可以凑出金额j-coins[i],则说明存在一种硬币组合可以凑出金额j,将dp[j]设置为true。
最后,统计dp数组中为true的元素个数,即为必须被使用的硬币种类的数量。并输出这些必须使用的硬币面值。
第4题:公共子序列
我们称序列 Z = < z1, z2, …, zk >是序列 X = < x1, x2, …, xm >的子序列当且仅当存在 严格上升 的序列< i1, i2, …, ik >, 使得对 j = 1, 2, … ,k, 有xij = zj。 比如 Z = < a, b, f, c > 是 X = < a, b, c, f, b, c >的子序列。 现在给出两个序列 X 和 Y, 你的任务是找到 X 和 Y 的最大公共子序列, 也就是说要找到一个最长的序列 Z, 使得 Z 既是 X 的子序列也是 Y 的子序列。
时间限制: 3000
内存限制: 65536
输入
输入包括多组测试数据。 每组数据包括一行, 给出两个长度不超过200 的字符串, 表示两个序列。 两个字符串之间由若干个空格隔开。
输出
对每组输入数据, 输出一行, 给出两个序列的最大公共子序列的长度。
样例输入
abcfbc abfcab
programming contest
abcd mnp
样例输出
4
2
0
要解决最大公共子序列问题,可以使用动态规划的方法。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <string.h>#define MAX_LENGTH 200int max(int a, int b) {return (a > b) ? a : b;
}int longestCommonSubsequence(char X[], char Y[], int m, int n) {int dp[MAX_LENGTH + 1][MAX_LENGTH + 1];for (int i = 0; i <= m; i++) {for (int j = 0; j <= n; j++) {if (i == 0 || j == 0) {dp[i][j] = 0;} else if (X[i - 1] == Y[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[m][n];
}int main() {char X[MAX_LENGTH + 1];char Y[MAX_LENGTH + 1];while (scanf("%s %s", X, Y) != EOF) {int m = strlen(X);int n = strlen(Y);int length = longestCommonSubsequence(X, Y, m, n);printf("%d\n", length);}return 0;
}
该代码使用一个二维数组dp来保存状态,其中dp[i][j]表示序列X的前i个字符和序列Y的前j个字符的最大公共子序列的长度。
首先,将dp[i][0]和dp[0][j]都设置为0,表示当一个序列的长度为0时,最大公共子序列的长度为0。
然后,从1到m和1到n的循环遍历,如果X[i-1]等于Y[j-1],则说明X的第i个字符和Y的第j个字符相同,将dp[i][j]设置为dp[i-1][j-1]的值加1,表示当前字符可以加入最大公共子序列。
如果X[i-1]不等于Y[j-1],则说明X的第i个字符和Y的第j个字符不相同,需要在X的前i-1个字符和Y的前j个字符的最大公共子序列和X的前i个字符和Y的前j-1个字符的最大公共子序列之间取最大值,即dp[i-1][j]和dp[i][j-1]的最大值。
最后,dp[m][n]即为X和Y的最大公共子序列的长度。
相关文章:

2022年03月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:拦截导弹 某国为了防御敌国的导弹袭击, 发展出一种导弹拦截系统。 但是这种导弹拦截系统有一个缺陷: 虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。 某天, 雷达捕捉到敌国的…...
)
五公里场地训练笔记(完整版)
由于考研和口罩等原因,停跑了比较长的时间。中长距离就是这样,修为尽失,大概是要从头开始了,不过还是要乐观的面对,CHEER UP! 翻看咕咚软件,以前的PB是21:12,在2017年9月…...
【电能质量扰动】基于ML和DWT的电能质量扰动分类方法研究(Matlab实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

使用 OpenAI GPT 模型的最佳实践
推荐:使用NSDT场景编辑器助你快速搭建可二次编辑的3D应用场景 为了帮助用户获得最佳输出,OpenAI 提供了使用 GPT 模型的最佳实践。这来自体验,因为许多用户不断尝试使用此模型并找到了最有效的方法。 在本文中,我将总结使用 Ope…...
解除用户账户控制提醒
解决用户账户控制提醒 1. 前言2. 解决用户账户控制提醒2.1 控制面板2.2 注册表2.3 UAC服务 结束语 1. 前言 当我们使用电脑时,有时进行安装应用或者打开应用时,总会弹出一个提示框,要选择点击是否允许程序运行; 系统经常弹出用户…...
行业追踪,2023-08-23
自动复盘 2023-08-23 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...

算法修炼Day60|● 84.柱状图中最大的矩形
LeetCode:84.柱状图中最大的矩形 84. 柱状图中最大的矩形 - 力扣(LeetCode) 1.思路 双指针思路,以当前数组为中心,借助两个数组存放当前数柱左右两侧小于当前数柱高度的索引,进行h*w的计算。注意首尾节点的左侧索引…...
)
前端面试题css(一)
题目 盒子垂直水平居中如何实现text-align:center vertical-align: middle水平垂直居中布局positionmargin水平垂直居中布局 grid栅格化布局及其兼容性介绍一下BFC触发 BFC 的条件包括:常见的用途包括: 写过的动画效果overflow有哪些属性visible&#x…...

.NETCORE中关于swagger的分组
有些时候我们的项目接口过多,就希望对应的swagger能够执行分组,网络上的几乎是千篇一律的分组方法,会累死! 这里提供一个更加高效的分组方法,比如你可以说哪些模块分到哪个组,哪些权限分到哪个组ÿ…...

4.1011
目录 四次挥手中收到乱序的FIN包会如何处理? 在 TIME_WAIT 状态的 TCP 连接,收到 SYN 后会发生什么? 四次挥手中收到乱序的FIN包会如何处理? 如果FIN报文比数据包先道道客户端,此时FIN是一个乱序报文,此时…...

uniapp中引入axios的错误?
场景 在unaipp中使用axios npm i axios 下载完成后 然后在页面中使用 axios.get(“http://3000/searchS”) 然后报错 Adapter http’ is not available in the build 原因 在 UniApp 中使用 Axios 发送 HTTP 请求时,如果出现错误 “Adapter http’ is not available…...

Discuz!论坛发帖标题字数限制80字符可以修改吗?修改发帖标题字数的方法
Discuz!论坛发帖标题字数限制80字符修改方法 1.数据库修改2.修改JS验证字符数文件3.修改模板中写死的字符限制数4.修改函数验证文件5.修改语言包文件6.更新缓存 Discuz X3.4论坛网站帖子标题字数限制80字符,当我们想使用长标题的时候就得一删再删,实在是…...
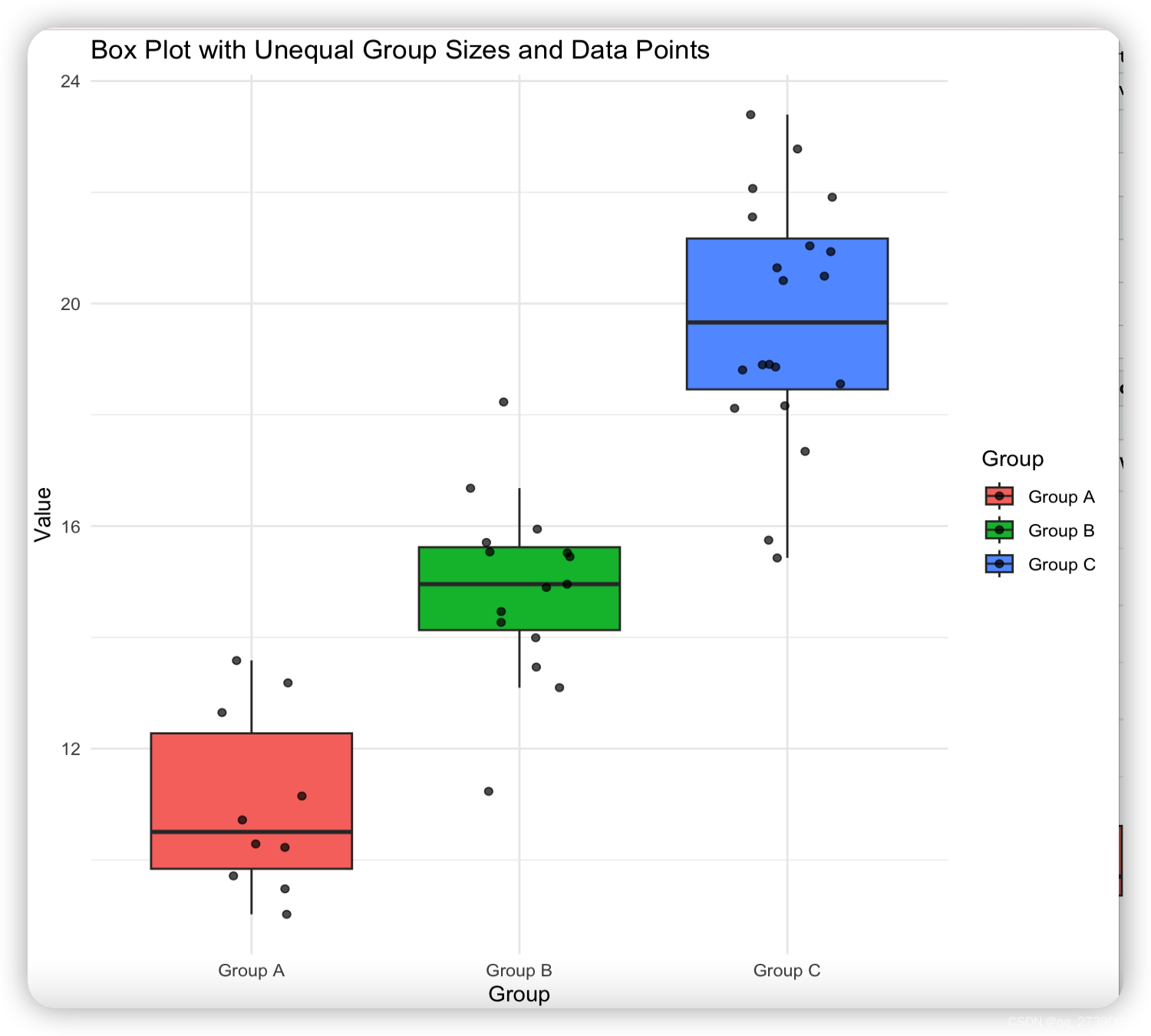
R语言画样本不均衡组的箱线图
# 导入 ggplot2 包 library(ggplot2)# 示例数据框,包含数值数据和分组信息 data <- data.frame(Group c(rep("Group A",10), rep("Group B",15),rep("Group C",20)),Value c(rnorm(10, mean 10, sd 2),rnorm(15, mean 15, sd…...
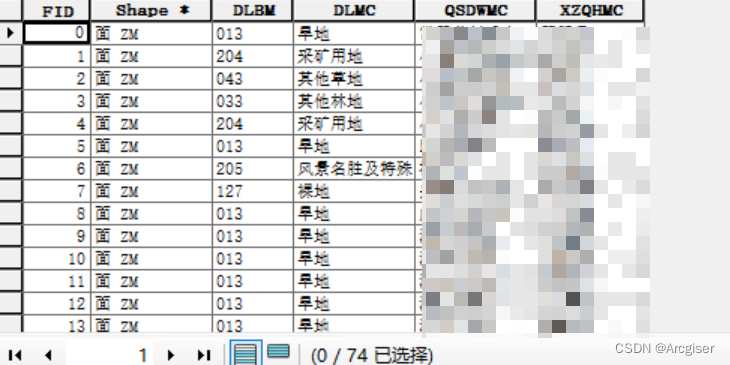
ArcGIS学习总结(19)——要素转点与空间连接(属性表字段映射)
1.在新创建的面矢量数据的属性表中没有对应的字段信息,为了能够和有属性信息的数据进行匹配,使其具有对应字段的信息。 2.需要匹配的矢量文件属性表信息。 3.对新创建的矢量文件执行要素转点:数据管理工具→要素→要素转点。 4.选择分析工…...

【每日一题Day306】LC228汇总区间 | 双指针
汇总区间【LC228】 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区间范…...
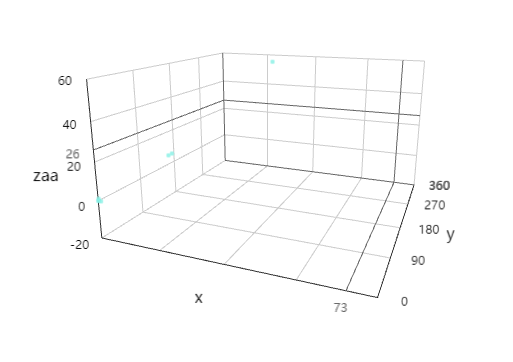
vue中实现echarts三维散点图
需要安装 echarts 同时引入 echarts-gl 我安装的版本: "echarts": "^5.3.2", "echarts-gl": "^2.0.9", import Vue from "vue"; import * as echarts from "echarts"; Vue.prototype.$echarts echa…...

多头自注意力机制的代码实现
文章目录 1、自注意力机制2、多头注意力机制 transformer的整体结构: 1、自注意力机制 自注意力机制如下: 计算过程: 代码如下: class ScaledDotProductAttention(nn.Module):def __init__(self, embed_dim, key_size, value_…...

抽象工厂模式
目录 了解抽象工厂模式前的前置知识 什么是抽象工厂模式? 为什么要提出抽象工厂模式? 抽象工厂模式中的四大角色? 抽象工厂模式的优缺点? 抽象工厂模式的适用场景? 了解抽象工厂模式前的前置知识 在讲抽象工厂模式…...
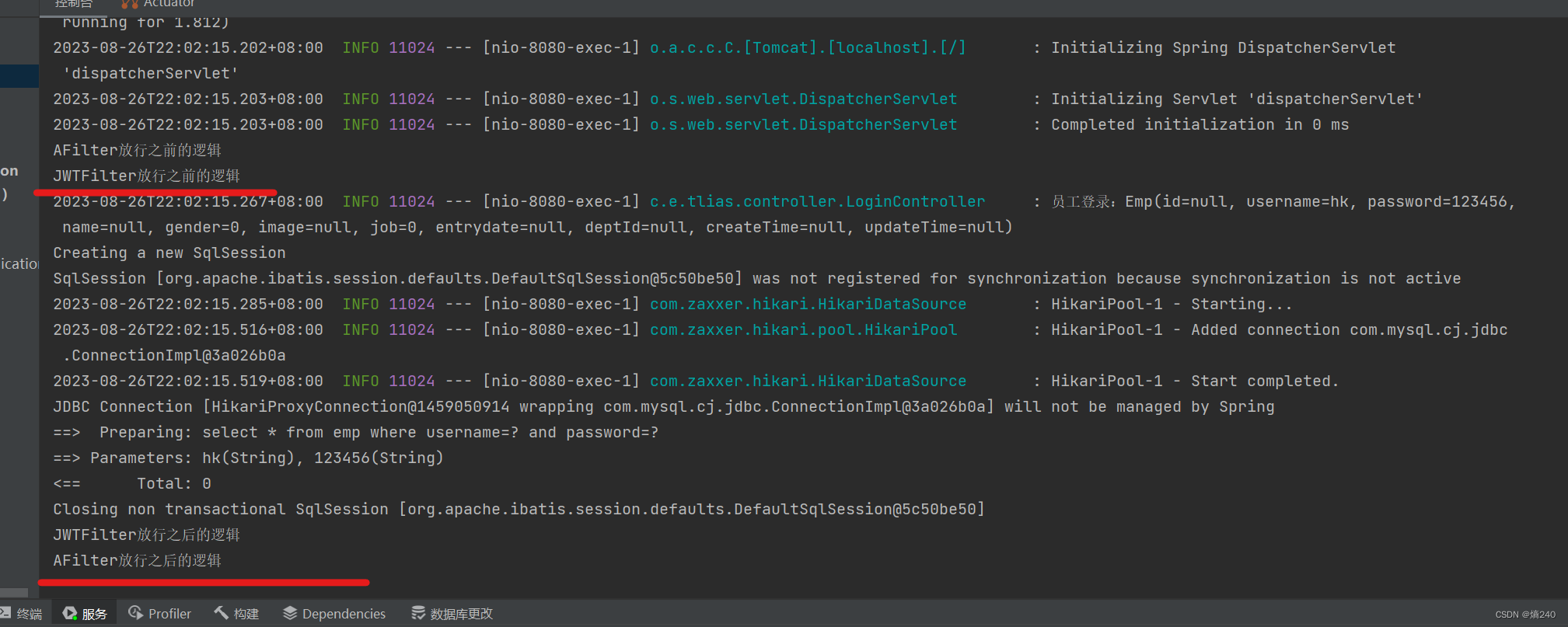
登录校验-Filter-详解
目录 执行流程 拦截路径 过滤器链 小结 执行流程 过滤器Filter拦截到请求之后,首先执行方放行之前的逻辑,然后执行放行操作(doFilter),然后会访问对应的Web资源(对应的Controller类)&#…...

堆栈方法区笔记记录
成员变量分两种: 1)实例变量:没有static修饰,属于对象,存储在堆中,有几个对象就有几份,通过对象点来访问 2)静态变量:由static修饰,属于类,存储在方法区中,只有一份,通过类名点来访…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
