并查集(种类并查集,带权并查集)
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
题目描述
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B,B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是“1 X Y”,表示X和Y是同类。
第二种说法是“2 X Y”,表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1≤N≤50,000)和K句话(0≤K≤100,000),输出假话的总数。
输入描述:
第一行是两个整数N和K,以一个空格分隔。 以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。 若D=1,则表示X和Y是同类。 若D=2,则表示X吃Y。
输出描述:
只有一个整数,表示假话的数目。
种类并查集
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
ll n;
ll fa[150004];
ll find(ll x)
{return x==fa[x]?x:fa[x]=find(fa[x]);
}
void merge(ll a,ll b)
{a=find(a),b=find(b);fa[a]=b;
}
void solve()
{ll n,k;cin>>n>>k;ll ans=0;for(ll i=1;i<=150003;i++){fa[i]=i;}ll op,x,y;for(ll i=0;i<k;i++){cin >> op >> x >> y;if (x > n || y > n || (op == 2 && x == y)) {ans++;continue;}if (op == 1) {if (find(x) == find(y + n) || find(x) == find(y + 2 * n)) {ans++;}else {merge(x, y);merge(x + n, y + n);merge(x + 2 * n, y + 2 * n);}}else {if (find(x) == find(y) || find(x) == find(y + 2 * n)) {ans++;}else {merge(x, y + n);merge(x + n, y + 2 * n);merge(x + 2 * n, y);}}}cout<<ans<<'\n';
}int main(){ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);ll t=1;while(t--)solve();return 0;}带权并查集
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
ll n;
ll fa[50004];
ll re[50004];
ll find(ll x)
{if(x!=fa[x]){ll t=fa[x];fa[x]=find(fa[x]);re[x]=(re[x]+re[t])%3;}return fa[x];
}
void merge(ll a,ll b,ll k)//012,同类,捕食,被捕食
{ll x=find(a),y=find(b);if(a!=b){fa[x]=y;re[x]=(k+re[b]-re[a]+3)%3;}
}
void solve()
{for(ll i=1;i<=50002;i++){fa[i]=i;re[i]=0;}ll n,k;cin>>n>>k;ll nums=0;for(ll i=1;i<=k;i++){ll d,x,y;cin>>d>>x>>y;ll a=find(x),b=find(y);if(x>n||y>n||(d==2&&x==y)){nums++;}else if(d==1){if(a!=b){merge(x,y,0);}else if(re[x]!=re[y]){nums++;}}else{if(a!=b){merge(x,y,1);}else if((re[x]-re[y]+3)%3!=1){nums++;}}}cout<<nums;
}int main(){ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);ll t=1;while(t--)solve();return 0;}相关文章:
)
并查集(种类并查集,带权并查集)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B,B吃C,C吃A。 现有N个动物,以1-N编号。每个动物都…...

飞天使-k8s基础组件分析-控制器
文章目录 控制器含义解释pod的标签与注释ReplicaControllerReplicaSetDeploymentsDaemonSetJobCronjob参考文档 控制器含义解释 空调遥控器知道吧ReplicationController: ReplicationController确保在任何时候都运行指定数量的pod副本。换句话说,一个ReplicationCo…...
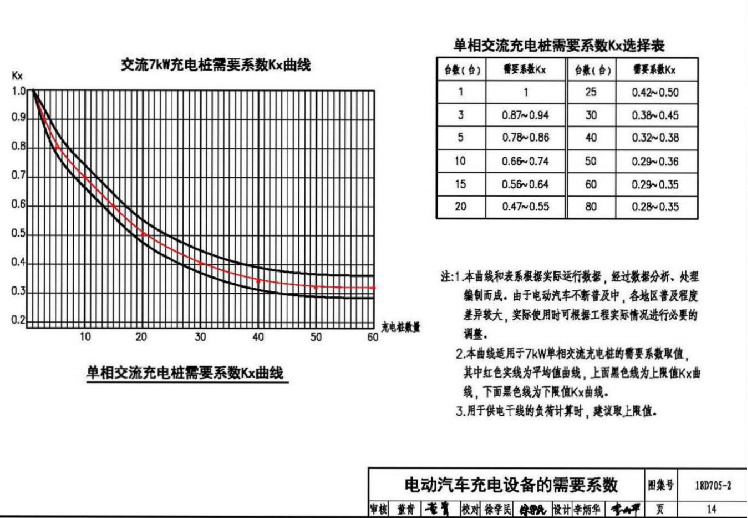
有序充电运营管理平台是基于物联网和大数据技术的充电设施管理系统-安科瑞黄安南
随着我国能源战略发展以及低碳行动的实施,电动汽车已逐步广泛应用,而电动汽车的应用非常符合当今社会对环保意识的要求,以及有效节省化石燃料的消耗。 由于其没有污染排放的优点以及政府部门的关注,电动汽车将成为以后出行的重要…...

LeetCode-227-基本计算器Ⅱ
题目描述: 给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。 整数除法仅保留整数部分。 你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。 注意:不允许使用任何将字符串作为数学表达式计…...

dart 学习列表 List
List 列表 在 Dart 编程语言中,List 是一种有序的集合数据类型,用于存储一系列项目。它允许您在单个变量中存储多个项目,并提供了许多操作来管理列表中的数据。以下是关于 Dart 中的 List 的一些重要信息: 创建 List: …...
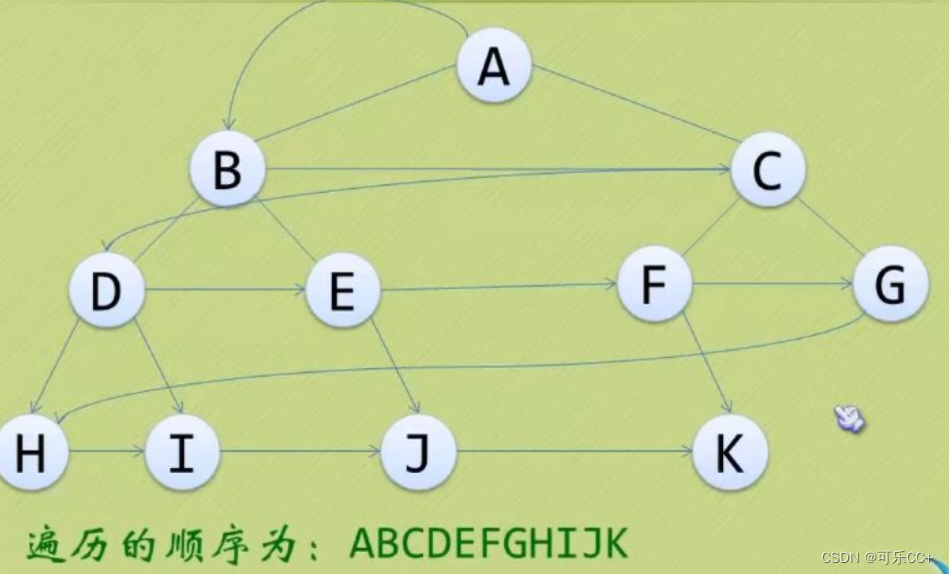
数据结构--树4.2.1(二叉树)
目录 一、二叉树的存储结构 二、二叉树的遍历 一、二叉树的存储结构 顺序存储结构:二叉树的顺序存储结构就是用一维数组存储二叉树中的各个结点,并且结点的存储位置能体现结点之间的逻辑关系。 链式存储结构:二叉树每个结点最多只有两个孩…...
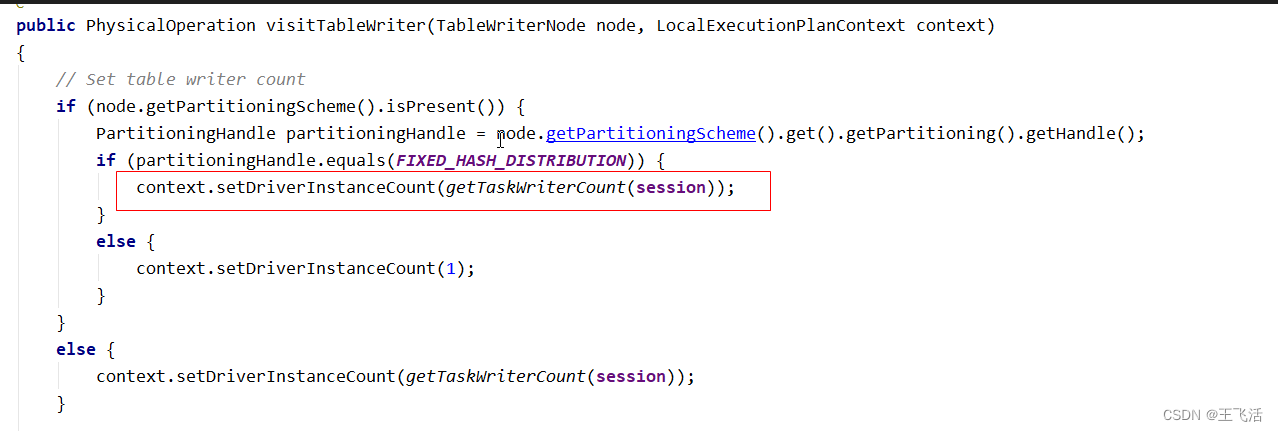
Presto之Driver个数
一. 前言 在Presto的Stage Performace中,每个Operator中都会有Driver个数的显示,如下图所示。本文主要介绍Presto中是如何决定Driver的个数的。 二. Driver个数 在Presto中,一个pipeline中启动多少个Driver,是由此Pipeline处理的S…...

R语言响应面(RSM)、线性模型lm分析生产过程影响因素可视化
全文链接:https://tecdat.cn/?p33499 响应面(Response Surface Methodology,RSM)分析是一种常用的统计方法,用于研究和优化生产过程中的影响因素。通过建立数学模型来描述因素与响应之间的关系,RSM可以帮助…...

剑指Offer --- 字符串篇
剑指Offer — 字符串篇 — 剑指的题解K神已经写的已经非常详细了,并且Github上开源的电子书目前热度也非常高,这个12天12个模块系列就当作自己的秋招刷题汇总了,欢迎大家交流。 剑指 Offer 05. 替换空格 思路 **(线性扫描) ** O(n) 这个…...
7.elasticsearch同步工具-logstah
1.logstah Logstash 是一个用于数据处理和转换的开源工具,它可以将来自不同源头的数据收集、转换、过滤,并将其发送到不同的目标。Logstash 是 ELK(Elasticsearch、Logstash 和 Kibana)技术栈的一部分,通常与 Elastics…...
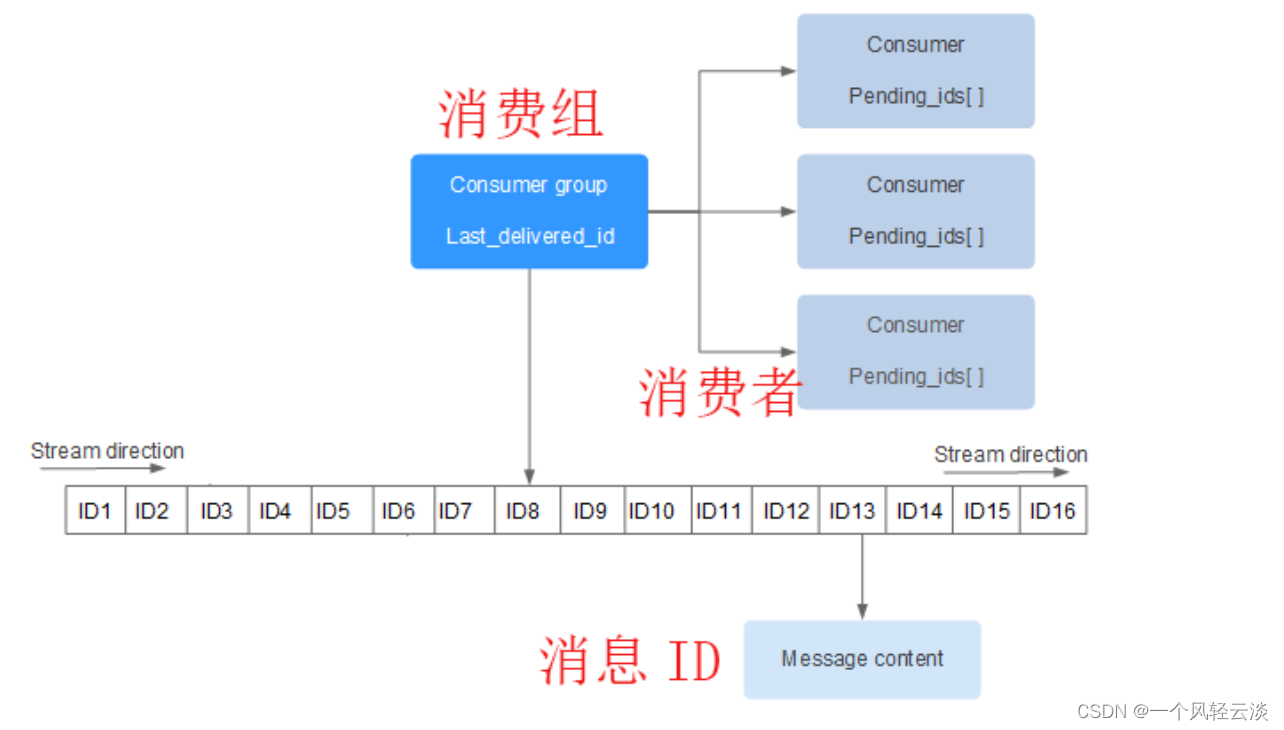
Redis之stream类型解读
目录 基本介绍 数据结构 消息 消费组 消费者 基本使用命令 概述 xadd 命令 xtrim 命令 xdel 命令 xlen 命令 xrange 命令 xread 命令 xgroup 命令 xreadgroup 命令 xack 命令 基本介绍 Redis stream(流)是一种数据结构,其…...
C++ 网络编程项目fastDFS分布式文件系统(九)总结
1. Location语法 1. 语法规则 location [ |~|~ * |^~ ] /uri/ { … } 正则表达式中的特殊字符 : - . () {} [] * ? 2. Location 优先级说明 在 nginx 的 location 和配置中 location 的顺序没有太大关系。 与 location 表达式的类型有关。 相同类型的表达式&a…...
第五章 树与二叉树 一、树的定义与考点
一、定义 1.树是由n (n > 0) 个节点组成的有限集合。 2.当n0时,称为空树。 3.在非空树中,有且仅有一个节点没有前驱,其他节点都有且仅有一个前驱,称为根节点。 4.每个节点有零个或多个子节点,而每个子节点又有零…...
C语言基础之——指针(下)
前言:本篇文章将继续讲解有关指针的剩余基础知识。 学无止境,一起加油叭!! 目录 一.指针运算 1.指针 - 整数 2.指针的关系运算 3.指针 - 指针 二.指针与数组 三.二级指针 四.指针数组 总结 一.指针运算 指针运算包括以下三…...
小研究 - JVM 的类装载机制
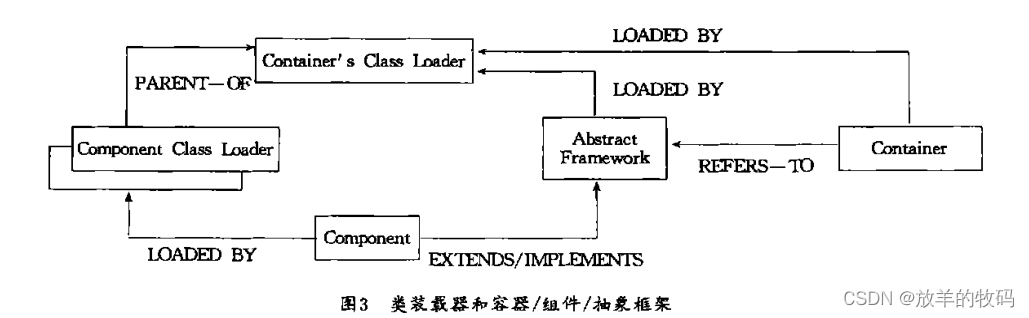
本文通过对一个类装载实例的分析,阐明了 Java虚拟机的类装载的代理机制和由此定义的命名空间,指出了类装载机制在容器/组件/抽象框架结构中的作用。 目录 1 引言 2 实例 3 分析 3.1 类装载的代理机制 3.2 Java的命名空间 3.3 解决问题 4 应…...
项目---日志系统
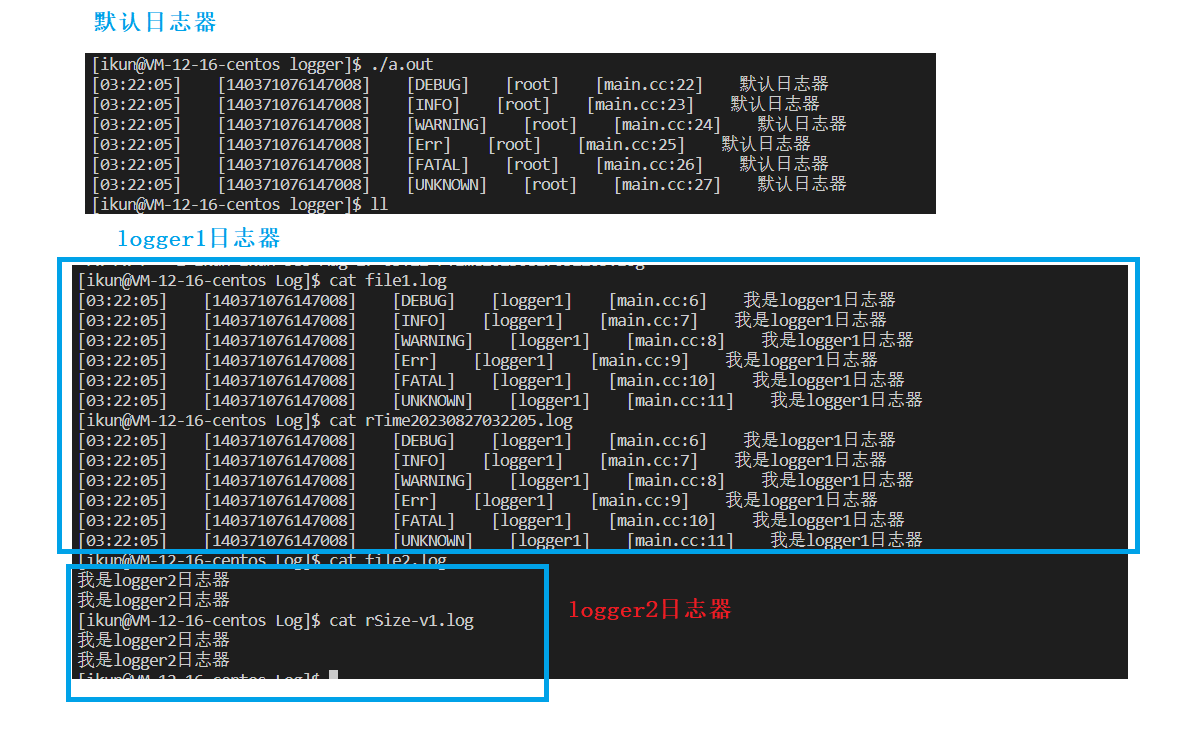
目录 项目系统开发环境核心技术日志系统介绍为什么需要日志系统? 日志系统框架设计日志系统模块划分代码实现通用工具实现日志等级模块实现日志消息模块实现格式化模块实现落地模块实现日志器模块同步日志器异步日志器缓冲区实现异步工作器实现 回归异步日志器模块建造者模式日…...

设计模式--建造者模式(Builder Pattern)
一、什么是建造者模式 建造者模式(Builder Pattern)是一种创建型设计模式,它关注如何按照一定的步骤和规则创建复杂对象。建造者模式的主要目的是将一个复杂对象的构建过程与其表示分离,从而使同样的构建过程可以创建不同的表示。…...
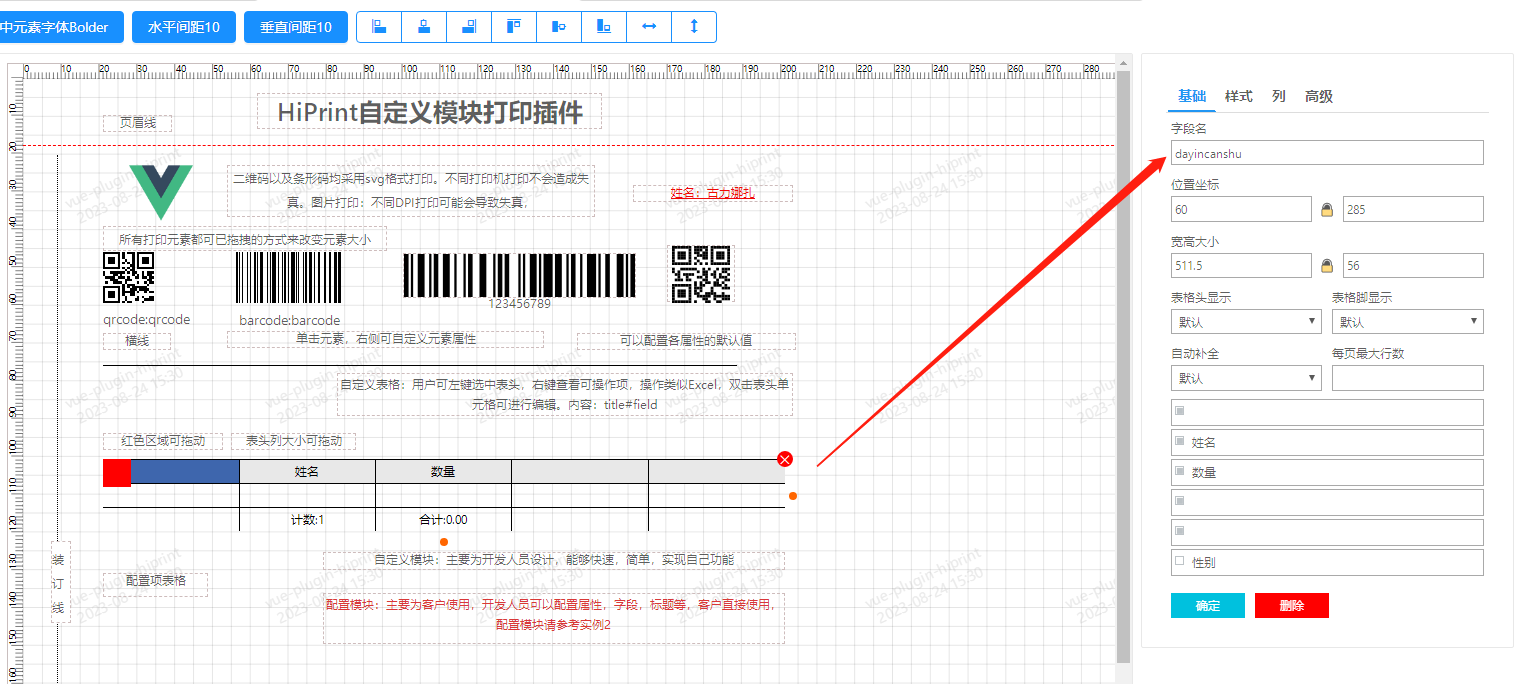
若依vue打印的简单方法
像我们后端程序员做前端的话,有时候真不需要知道什么原理,直接塞就好了 我们选用基于hiprint 的vue-plugin-hiprint来打印 目的是为了实现点击某些行的数据,然后点击某个按钮直接弹出下面的打印 此链接 大佬是原创,我拿来总结梳理一下 插件进阶功能请移步: 链接 插件模板制作页…...

Rust 基础语法学习
Rust 基础语法学习 文章目录 Rust 基础语法学习hello world变量数据类型整数类型进制表示方法浮点数类型布尔类型字符类型字符串复合类型元组结构体元组结构体 切片类型字符串切片数组切片 不可变变量与可变变量常量注释函数语句与表达式 流程控制语句if else条件判断while循环…...

iOS开发Swift-函数
1.函数的定义和调用 func greet(person: String) -> String { // 函数名 传入值 传入值类型 返回值类型let greeting "Hello" personreturn greeting } print( greet(person: "Anna") ) //调用2.函数的参数与返回值 (1)无参函数 func sayHe…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
