【图论】缩点的综合应用(一)
一.缩点的概念
![]()
缩点,也称为点缩法(Vertex Contraction),是图论中的一种操作,通常用于缩小图的规模,同时保持了图的某些性质。这个操作的目标是将图中的一些节点合并为一个超级节点,同时调整相关边,以便保持图的连通性和其他性质。
具体步骤如下:
-
选择一个要缩点的节点:选择图中的一个节点,将它合并到另一个节点上。
-
合并节点:将选定的节点合并到另一个节点上,形成一个新的超级节点。通常情况下,选择入度或出度较小的节点进行合并,以减小新图的规模。
-
调整边:将与被合并节点相邻的边重新连接到新的超级节点上。注意要避免重复边和自环。
-
重复步骤1~3:继续选择节点进行缩点,直到不满足合并条件为止。
缩点操作通常用于算法设计和图分析中,有时可以用来简化图的复杂性,减少问题的规模。在一些情况下,缩点操作可能会破坏某些图的属性,因此在使用时需要谨慎考虑。此外,缩点操作后的图可能不再是原始问题的精确表示,可能会导致问题的近似解。
二.缩短的作用
把一个环缩为一个超级点,可以由有环图-->DAG,从而更好的解决问题。
总之就是我们不想要环,直接缩为一个点,我们可以更好地解决问题,就就可以使用缩点法。
三.模板题
P3387 【模板】缩点 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
四.思路
1.求点权之和最大,我们可以想到什么?最小生成树。
2.但这只需要解决一条路径的点权值最大,那可以怎么解决?拓扑+DP。
3.但是...拓扑只能解决DAG,这有环啊!!! 我们把环缩成一个超级点,然后再建一个新图不就行了吗?理论通过,实践开始!
五.实践
(1)tarjan缩点
主函数部分:
scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&p[i]);}for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);add(u,v);}for(int i=1;i<=n;i++){if(!dfn[i]) tarjan(i);}tarjan:
void tarjan(int u){dfn[u]=low[u]=++num;sta[++top]=u;ins[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(!dfn[v]){tarjan(v);low[u]=min(low[u],low[v]);}else if(ins[v]){low[u]=min(low[u],dfn[v]);}}if(dfn[u]==low[u]){int j=0;while(1){j=sta[top--];ins[j]=0;h[j]=u; //j从此属于u if(j==u) break;p[u]+=p[j]; //点权值合并到第一个点(u点)上 }}
}(2)重新建图
for(int i=1;i<=m;i++){int u=h[edge[i].u],v=h[edge[i].v];if(u!=v){ //不在一个环 add2(u,v);in[v]++; //入度++,拓扑用 }}(3)拓扑排序+DP
int topu(){queue<int> q;for(int i=1;i<=n;i++){ if(!in[i] && i==h[i]){q.push(i); //这是这条路径的起点 dp[i]=p[i]; //记得赋值 } }//拓扑基础 while(!q.empty()){int k=q.front(); q.pop();for(int i=head2[k];i;i=ed[i].next){int v=ed[i].v;dp[v]=max(dp[v],dp[k]+p[v]);in[v]--;if(!in[v]) q.push(v);}}//找最大值,不一定n就最大,毕竟不止一条路 int ans=0;for(int i=1;i<=n;i++){ans=max(ans,dp[i]);}return ans;
}六.参考代码(完整代码)
#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
int p[maxn];
struct Edge{int u,v,next;
}edge[maxn],ed[maxn];
int head[maxn],head2[maxn],cnt,cnt2;
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
void add2(int u,int v){ed[++cnt2]=(Edge){u,v,head2[u]}; head2[u]=cnt2;
}
int dfn[maxn],low[maxn],num;
int sta[maxn],ins[maxn],top;
int lg,h[maxn]; //环的个数,成员属于哪个环
void tarjan(int u){dfn[u]=low[u]=++num;sta[++top]=u;ins[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(!dfn[v]){tarjan(v);low[u]=min(low[u],low[v]);}else if(ins[v]){low[u]=min(low[u],dfn[v]);}}if(dfn[u]==low[u]){int j=0;while(1){j=sta[top--];ins[j]=0;h[j]=u; //j从此属于u if(j==u) break;p[u]+=p[j]; //点权值合并到第一个点(u点)上 }}
}
int in[maxn],dp[maxn];
int topu(){queue<int> q;for(int i=1;i<=n;i++){ if(!in[i] && i==h[i]){q.push(i); //这是这条路径的起点 dp[i]=p[i]; //记得赋值 } }//拓扑基础 while(!q.empty()){int k=q.front(); q.pop();for(int i=head2[k];i;i=ed[i].next){int v=ed[i].v;dp[v]=max(dp[v],dp[k]+p[v]);in[v]--;if(!in[v]) q.push(v);}}//找最大值,不一定n就最大,毕竟不止一条路 int ans=0;for(int i=1;i<=n;i++){ans=max(ans,dp[i]);}return ans;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&p[i]);}for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);add(u,v);}for(int i=1;i<=n;i++){if(!dfn[i]) tarjan(i);}for(int i=1;i<=m;i++){int u=h[edge[i].u],v=h[edge[i].v];if(u!=v){ //不在一个环 add2(u,v);in[v]++; //入度++,拓扑用 }}cout<<topu();return 0;
}相关文章:

【图论】缩点的综合应用(一)
一.缩点的概念 缩点,也称为点缩法(Vertex Contraction),是图论中的一种操作,通常用于缩小图的规模,同时保持了图的某些性质。这个操作的目标是将图中的一些节点合并为一个超级节点,同时调整相关…...

C++—纯虚函数
一、前言 定义一个函数为虚函数,不代表函数为不被实现的函数。 定义函数为虚函数是为了允许用基类的指针来调用子类的这个函数。 定义一个函数为纯虚函数,才代表函数没有被实现。 定义纯虚函数是为了实现一个接口,起到一个规范的作用&…...

经过卷积神经网络之后的图片的尺寸如何计算
经过卷积神经网络(Convolutional Neural Network,CNN)处理后,图片的尺寸会发生变化,这是由于卷积层、池化层等操作引起的。计算图片经过卷积神经网络后的尺寸变化通常需要考虑卷积核大小、步幅(stride&…...
,修改maven)
Java升级JDK17(更高版本同理),修改maven
记住三个网址就行:下面这个是oracle的 Java Platform, Standard Edition 17 ReferenceImplementations https://www.oracle.com/java/technologies/downloads/#jdk17-windows 另外一个 redhat旗下的:这个是开源的(推荐这个!&am…...
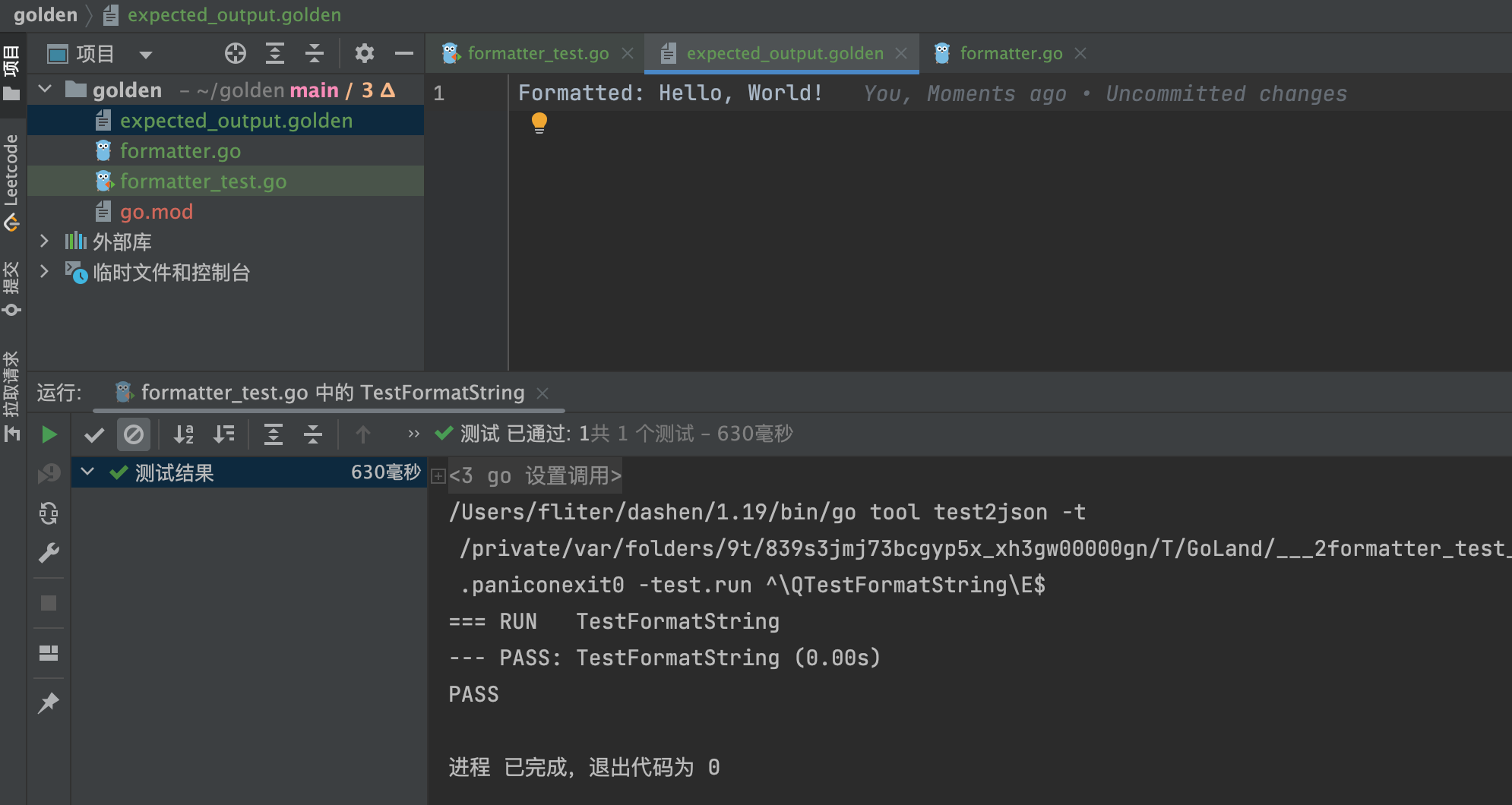
Go测试之.golden 文件
Go测试中的.golden 文件是干什么用的?请举例说明 在Go语言中,.golden文件通常用于测试中的黄金文件(golden files)。黄金文件是在测试期间记录预期输出结果的文件。测试用例运行时,黄金文件用于比较实际输出与预期输出…...

回归预测 | MATLAB实现GA-RF遗传算法优化随机森林算法多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现GA-RF遗传算法优化随机森林算法多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现GA-RF遗传算法优化随机森林算法多输入单输出回归预测(多指标,多图)效果一览基本介绍程…...
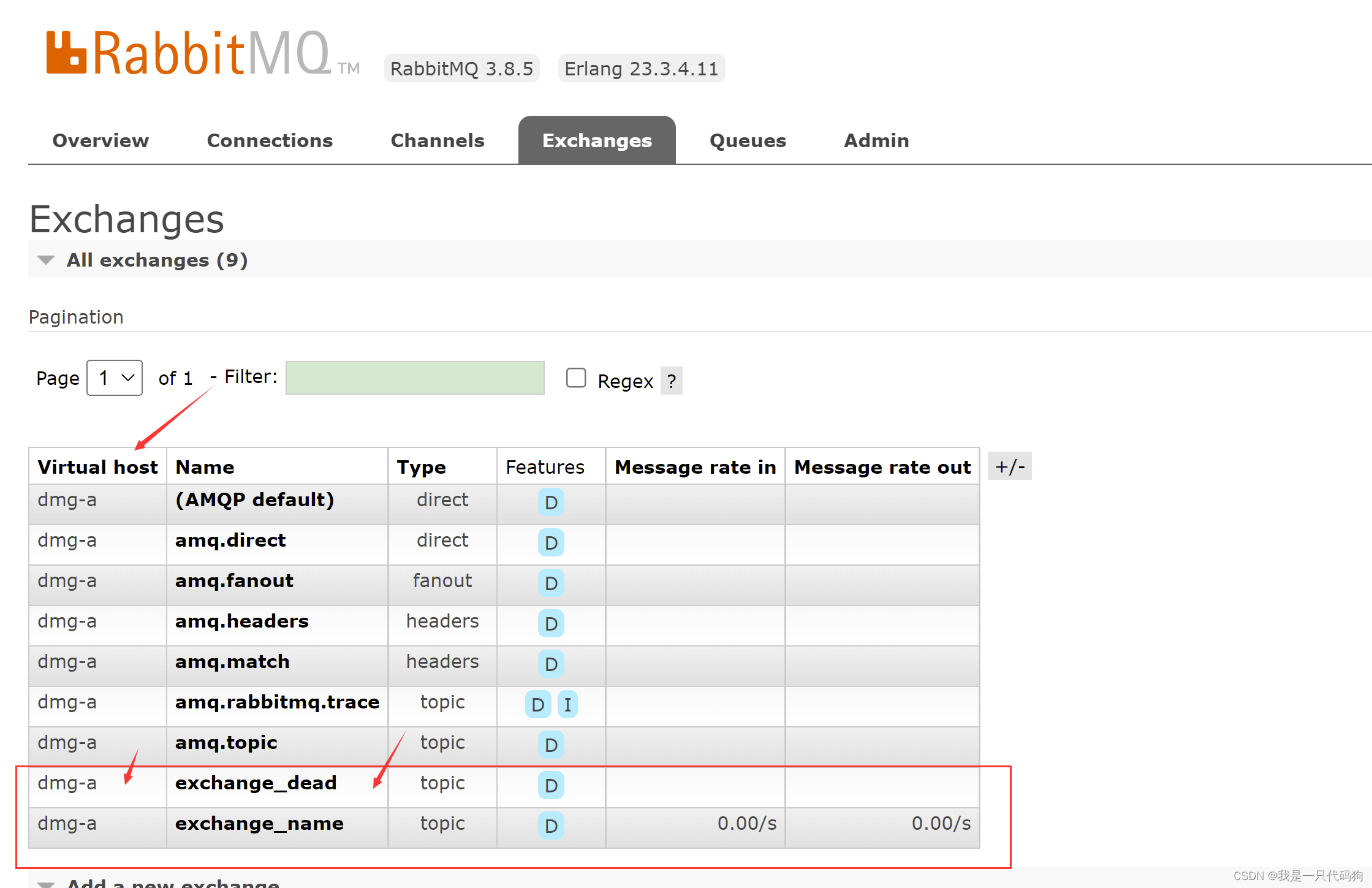
springboot整合rabbitmq死信队列
springboot整合rabbitmq死信队列 什么是死信 说道死信,可能大部分观众大姥爷会有懵逼的想法,什么是死信?死信队列,俗称DLX,翻译过来的名称为Dead Letter Exchange 死信交换机。当消息限定时间内未被消费,…...
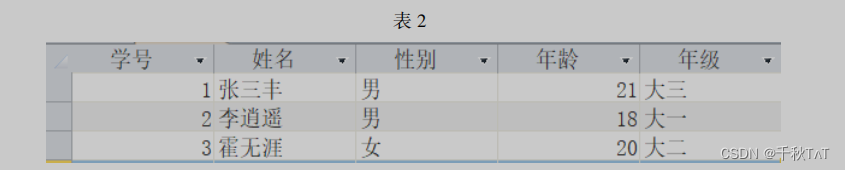
高中信息技术教资考试模拟卷(22下)
2022 年下半年全国教师资格考试模考卷一 (高中信息技术) 一、单项选择题(本大题共 15 小题,每小题 3 分,共 45 分) 1.2006 年 10 月 25 日,深圳警方成功解救出一名被网络骗子孙某…...

Linux中shadow及passwd格式内容解析
/etc/passwd文件包括Linux账号信息,示例如下: root:x:0:0:root:/root:/bin/bash bin:x:1:1:bin:/bin:/sbin/nologin daemon:x:2:2:daemon:/sbin:/sbin/nologin adm:x:3:4:adm:/var/adm:/sbin/nologin 具体格式 用户名࿱…...

计算机视觉 – Computer Vision | CV
计算机视觉为什么重要? 人的大脑皮层, 有差不多 70% 都是在处理视觉信息。 是人类获取信息最主要的渠道,没有之一。 在网络世界,照片和视频(图像的集合)也正在发生爆炸式的增长! 下图是网络上…...
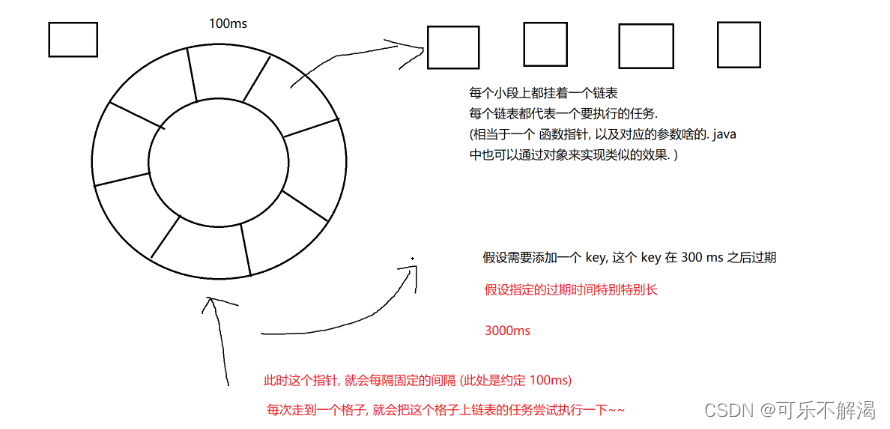
2.Redis 通用命令
Redis 中最核心的两个命令: set 作用:设置 key 对应的 value 值并存储进去。若key已包含一个值,则无论其类型如何,都会覆盖该值。在SET操作成功时,将丢弃与密钥相关联的任何先前生存时间。 对于上述这里的 key和val…...

【学习FreeRTOS】第18章——FreeRTOS软件定时器
1.软件定时器的简介 定时器:从指定的时刻开始,经过一个指定时间,然后触发一个超时事件,用户可自定义定时器的周期硬件定时器:芯片本身自带的定时器模块,硬件定时器的精度一般很高,每次在定时时…...

C++--两个数组的dp问题(2)
1.交错字符串 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给定三个字符串 s1、s2、s3,请判断 s3 能不能由 s1 和 s2 交织(交错) 组成。 两个字符串 s 和 t 交织 的定义与过程如下,其中每个字符串都…...

利用人工智能彻底改变库存管理:综合指南
通过本指南了解人工智能如何增强库存管理,为希望简化运营的管理者和企业主提供帮助。 库存管理是任何销售实物产品的企业的重要组成部分。它包括跟踪库存水平,预测未来需求,并确保始终有足够的产品来满足客户需求,但又不会因库存过多而浪费金钱。有效的库存管理可以显着降…...

连接器信号完整性仿真教程 七
本将介绍微带线及差分微带线仿真。做连接器信号完整性仿真时,有时后没法将激励端口直接设置到连接器端子上,这就需画出连接器PCB PAD,将激励端口设置在PAD的端面上,或者用引线连接PAD,将引线引出到适当的位置ÿ…...
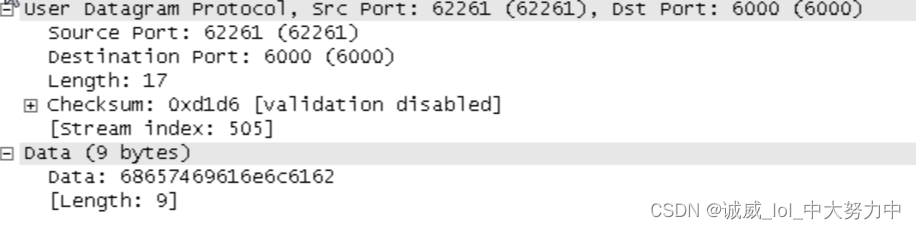
Wireshark数据抓包分析之UDP协议
一、实验目的: 通过使用wireshark对UDP数据包的抓取分析UDP协议的内容 二、预备知识: UDP协议的概念:UDP使用底层的互联网协议来传送报文,同IP一样提供不可靠的无连接传输服务。它也不提供报文到达确认、排序及流量控制等功能。 …...
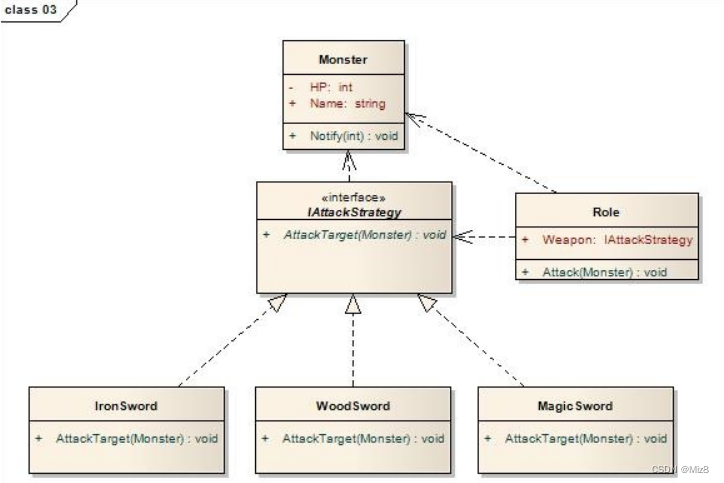
Java小游戏
一、需求 二、思路一 HP当然是怪物的一个属性成员,而武器是角色的一个属性成员,类型可以使字符串,用于描述目前角色所装备的武器。角色类有一个攻击方法,以被攻击怪物为参数,当实施一次攻击时,攻击方法被调…...
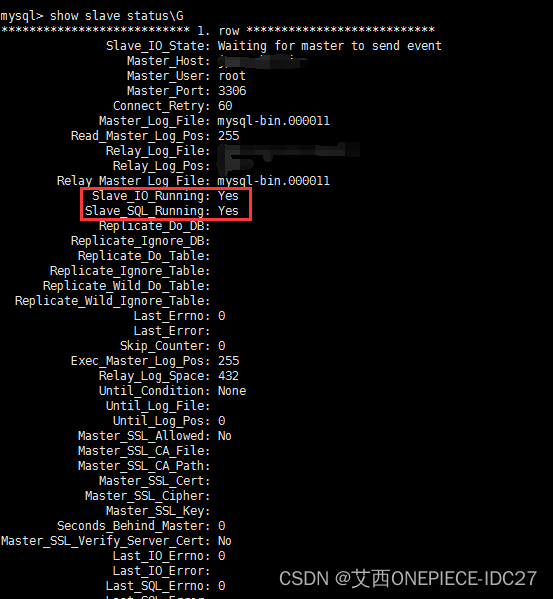
服务器Linux系统配置mysql数据库主从自动备份
服务器Linux系统配置mysql数据库主从自动备份 当数据内容越来越多的时候,数据库也变得越来越大了。如果不小心误删了,或者被黑主机了,那就什么都没有了。所以数据库的数据怎么能让它不丢失做到万无一失变得尤为重要! 我是艾西&a…...

Java通过PowerMockito和Mokito进行单元测试
PowerMockito和Mokito的概念 PowerMockito和Mockito都是Java语言中的测试框架,用于进行单元测试和集成测试。它们中的每一个都有不同的功能和应用。 Mockito是一个基于模拟的测试框架。它允许你模拟对象,在测试中隔离被测代码的依赖项。使用Mockito&am…...
数字化技术无限延伸,VR全景点亮智慧生活
随着互联网的发展,我们无时无刻不再享受着互联网给我们带来的便利,数字化生活正在无限延伸,各行各业也开始积极布局智能生活。要说智慧生活哪个方面应用的比较多,那应该就是VR全景了,目前VR全景已经被各个行业广泛应用…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
