二、数学建模之整数规划篇
1.定义
2.例题
3.使用软件及解题
一、定义
1.整数规划(Integer Programming,简称IP):是一种数学优化问题,它是线性规划(Linear Programming,简称LP)的一个扩展形式。在线性规划中,优化目标和约束条件都是线性的,而在整数规划中,除了这些线性约束外,变量还被限制为整数值。在整数规划问题中,我们需要在给定一组变量和一组线性约束条件的情况下,找到满足这些约束条件的整数值变量,使得一个特定的线性目标函数达到最大或最小。整数规划在实际问题中具有广泛的应用,例如生产调度、资源分配、物流规划、项目排程等。
2.与线性规划相比
整数规划问题更为复杂,因为整数变量引入了离散性,使得问题的解空间不再是连续的。这导致整数规划问题通常更难以求解,因为搜索整数解的空间相对于连续解的空间更大且不连续。
求解整数规划问题,需要使用专门的算法和工具,如分支定界法、割平面法、混合整数线性规划求解器等。这些方法通常会尝试在搜索整数解的过程中通过一系列的策略来逐渐缩小解空间,以找到最优的整数解。
3.整数规划分类(根据不同的特性和约束条件)
(1) 0-1整数规划:在这种问题中,变量被限制为取值为0或1,表示是否选择某个决策。这类问题的典型应用包括装载问题、投资决策问题等。
(2) 混合整数线性规划:在这类问题中,除了一部分变量可以取连续值外,还有一部分变量需要取整数值。MILP问题广泛应用于生产计划、物流网络优化等领域。
(3) 纯整数规划:所有的变量都必须取整数值,没有连续变量。这类问题在排产、任务分配等领域中常见。
(4) 多目标整数规划:在这种问题中,有多个优化目标需要同时考虑。这样的问题在多目标决策中很有用,例如平衡成本和资源利用率。
(5) 分支限界整数规划:这是一种常用的求解整数规划问题的方法。它通过逐步分解问题,并在每个分支上进行线性规划求解,然后根据解的上下界限制来确定是否进一步探索该分支。
(6) 割平面整数规划:在这种方法中,通过添加一系列的割平面约束来逐步缩小整数解空间,以逼近最优解。割平面法常用于求解MILP问题。
(7) 约束编程:这是一种用于求解离散优化问题的方法,它不仅适用于整数规划,还适用于更广泛的约束满足问题。在约束编程中,问题的变量和约束条件都可以具有不同的性质,如整数、集合等。
4.整数规划问题一般求解过程步骤
1.建立数学模型:
(1)确定决策变量:确定需要优化的变量,以及这些变量的含义和范围。
(2)确定目标函数:定义需要最大化或最小化的目标函数,通常是线性组合的形式。
(3)确定约束条件:列出问题的约束条件,这些条件限制了变量之间的关系。
2.线性规划求解:
(1)将整数规划问题转化为相应的线性规划问题,即将所有变量视为连续变量。
(2)使用线性规划求解器(如单纯形法、内点法等)求解得到线性规划的最优解。
3.检查解的整数性:
(1)如果线性规划的最优解是整数,那么整数规划问题的解已经找到,问题解决。
(2)如果线性规划的最优解不是整数,就需要继续进行下面的步骤。
4.分支定界法:
(1)选择一个分支变量:选择一个在线性规划解中取非整数值的变量作为分支变量。
(2)拆分问题:将问题分为两个子问题,一个限制该分支变量为下取整,另一个限制为上取整。
(3)对每个子问题重复求解的过程,直到找到整数解或者发现问题无解为止。
(4)在每次求解子问题时,可以使用割平面、启发式等方法来改善求解效率。
5.终止条件:
(1)当找到整数解时,检查是否比当前最优解更优,更新最优解。
(2)**当发现所有分支问题都没有整数解,或者问题的最优解已经被找到,终止求解过程。
6.输出结果:
返回找到的最优整数解或者近似整数解作为问题的解决方案。
5.求解方法分类及定义
(1))分枝定界法一可求纯或混合整数线性规划
对有约束条件的最优化问题(其可行解为有限数)的所有可行解空间恰当地进行系统搜索,这就是分枝与定界内容。通常,把全部可行解空间反复地分割为越来越小的子集,称为分枝;并且对每个子集内的解集计算一个目标下界(对于最小值问题),这称为定界。在每次分枝后,凡是界限超出已知可行解集目标值的那些子集不再进一步分枝,这样,许多子集可不予考虑,这称剪枝。
(2)割平面法—可求纯或混合整数线性规划。
(3)隐枚举法—求解0-1”整数规划。
过滤隐枚举法
分枝隐枚举法
(4)匈牙利法一解决指派问题(“0-1"规划特殊情形)。
(5)蒙特卡洛法—求解各种类型规划。
二、例题
1.分枝定界法




三、使用软件及解题
1.matlab求解
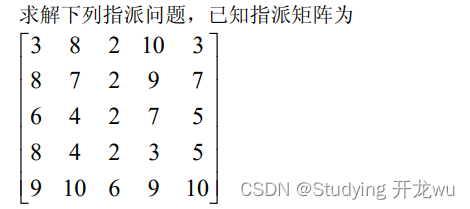
解法一:编写 Matlab 程序如下:
c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 58 4 2 3 5;9 10 6 9 10];
c=c(:);
a=zeros(10,25);
for i=1:5a(i,(i-1)*5+1:5*i)=1;a(5+i,i:5:25)=1;
end
b=ones(10,1);
[x,fval]=bintprog(c,[],[],a,b);
x=reshape(x,[5,5]), fval2.1.LINGO求解
求解法二:的LINGO程序如下
model:
sets:
var/1..5/;
link(var,var):c,x;
endsets
data:
c=3 8 2 10 38 7 2 9 76 4 2 7 58 4 2 3 59 10 6 9 10;
enddata
min=@sum(link:c*x);
@for(var(i):@sum(var(j):x(i,j))=1);
@for(var(j):@sum(var(i):x(i,j))=1);
@for(link:@bin(x));
end相关文章:

二、数学建模之整数规划篇
1.定义 2.例题 3.使用软件及解题 一、定义 1.整数规划(Integer Programming,简称IP):是一种数学优化问题,它是线性规划(Linear Programming,简称LP)的一个扩展形式。在线性规划中&…...

C语言日常刷题 4
文章目录 题目答案与解析123456 题目 1、设变量已正确定义,以下不能统计出一行中输入字符个数(不包含回车符)的程序段是( ) A: n0;while(chgetchar()!‘\n’)n; B: n0;while(getchar()!‘\n’)n; C: for(n0;getchar()…...
MyBatis plus 多数据源实现
1. 项目背景 最近写文章发布到【笑小枫】小程序和我的个人网站上,因为个人网站用的是halo框架搭建,两边数据结构不一致,导致我每次维护文章都需要两边维护,这就很烦~ 于是,本文就诞生了。通过项目连接这两个数据库&a…...

k-近邻算法概述,k-means与k-NN的区别对比
目录 k-近邻算法概述 k-近邻算法细节 k值的选取 分类器的决策 k-means与k-NN的区别对比 k-近邻算法概述 k近邻(k-nearest neighbor, k-NN)算法由 Cover 和 Hart 于1968年提出,是一种简单的分类方法。通俗来说,就是给定一个…...

node 项目搭建
1. 初始化项目 cmd 执行 cnpm init -y 创建README.md 依赖安装 1. 数据库 和 框架 mysql express cnpm install mysql express --save 2. 后端跨域 cors cnpm i cors 3. 安装 body-parser 声明引用 用于接收前端 post 过来的数据 cnpm install --save body-parser 4…...
CSS 属性值计算过程
目录 例子1,确定声明值2,层叠冲突2.1,比较源重要性2.2,比较优先级2.3,比较源次序 3,使用继承4,使用默认值其他 例子 我们来举例说明<h1> 标签最终的样式: <div><h1…...

QT版权查询
文章目录 QT工具版权QT模块版权查询 根据条件自动筛选: Qt Features, Framework Essentials, Modules, Tools & Add-Ons QT工具版权 Licensing QT模块版权查询 在 All Modules 中点击进入每个模块,在详细内容中一般有Lisence相关内容。 Licens…...

【leetcode 力扣刷题】双指针///原地扩充线性表
双指针///原地扩充线性表 剑指 Offer 05. 替换空格定义一个新字符串扩充字符串,原地替换思考 剑指 Offer 05. 替换空格 题目链接:剑指 Offer 05. 替换空格 题目内容: 这是一道简单题,理解题意,就是将字符串s中的空格…...

第八章,帖子列表
8.1添加帖子列表 <script> import { mapState } from vuex . . . </script> computed: {...mapState([auth,user,articles]) }, <Message :sh...

netty与websockt实现聊天
配置websockt: import lombok.Data; import org.springframework.boot.context.properties.ConfigurationProperties; import org.springframework.context.annotation.Configuration;/*** websocket配置*/ Data Configuration ConfigurationProperties(prefix &qu…...
21.2 CSS 三大特性与页面布局
1. 开发者工具修改样式 使用开发者工具修改样式, 操作步骤如下: * 1. 打开开发者工具: 在浏览器中右键点击页面, 然后选择检查或者使用快捷键(一般是 F12 或者 CtrlShiftI)来打开开发者工具.* 2. 打开样式编辑器: 在开发者工具中, 找到选项卡或面板, 一般是Elements或者Elemen…...

MySQL 特殊语法时间格式以及Greadb连接
一、时间语法 DATE_FORMAT和to_char() select to_char(now(),%Y-%m-%d %H:%i:%s) from dual; select DATE_FORMAT(now(),%Y-%m-%d %H:%i:%s) from dual; 2.to_date() 和STR_TO_DATE(#{date},%Y-%m-%d ) select to_date(now(),yyyy-mm-dd hh24:mi:ss) from dual;...
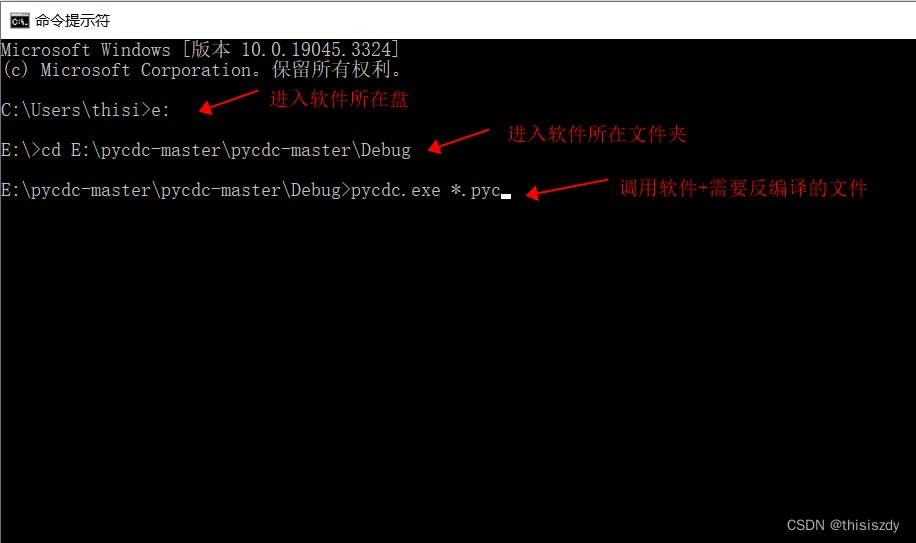
Python(.pyc)反编译:pycdc工具安装与使用
本文将介绍如何将python的.pyc文件反编译成源码,以便我们对源码的学习与改进。pycdc工具安装 下载地址: 1、Github地址:https://github.com/zrax/pycdc ,下载后需要使用CMake进行编译。 2、已下载好及编译好的地址:ht…...
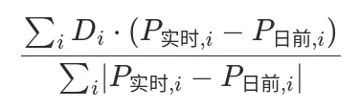
山西电力市场日前价格预测【2023-08-28】
日前价格预测 预测明日(2023-08-28)山西电力市场全天平均日前电价为319.70元/MWh。其中,最高日前电价为371.80元/MWh,预计出现在19: 15。最低日前电价为278.59元/MWh,预计出现在13: 00。 价差方向预测 1: …...

python3/pip3 SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed
环境: mac os 背景: 电脑之前安装的是python3.9 , 现在升级到python3.10。 从python官网下载macos版本的python3.10 pkg。 双击安装。 程序使用aiohttp访问ebay 。 出错: aiohttp.client_exceptions.ClientConnectorCertifi…...

Python中的迭代器与生成器
文章目录 1、迭代器2、生成器3、列表推导式和生成器表达式4、enumerate() 在Python中,迭代器(Iterator)和生成器(Generator)是两种用于处理可迭代对象的重要工具。而可迭代对象包括列表,元组,字…...
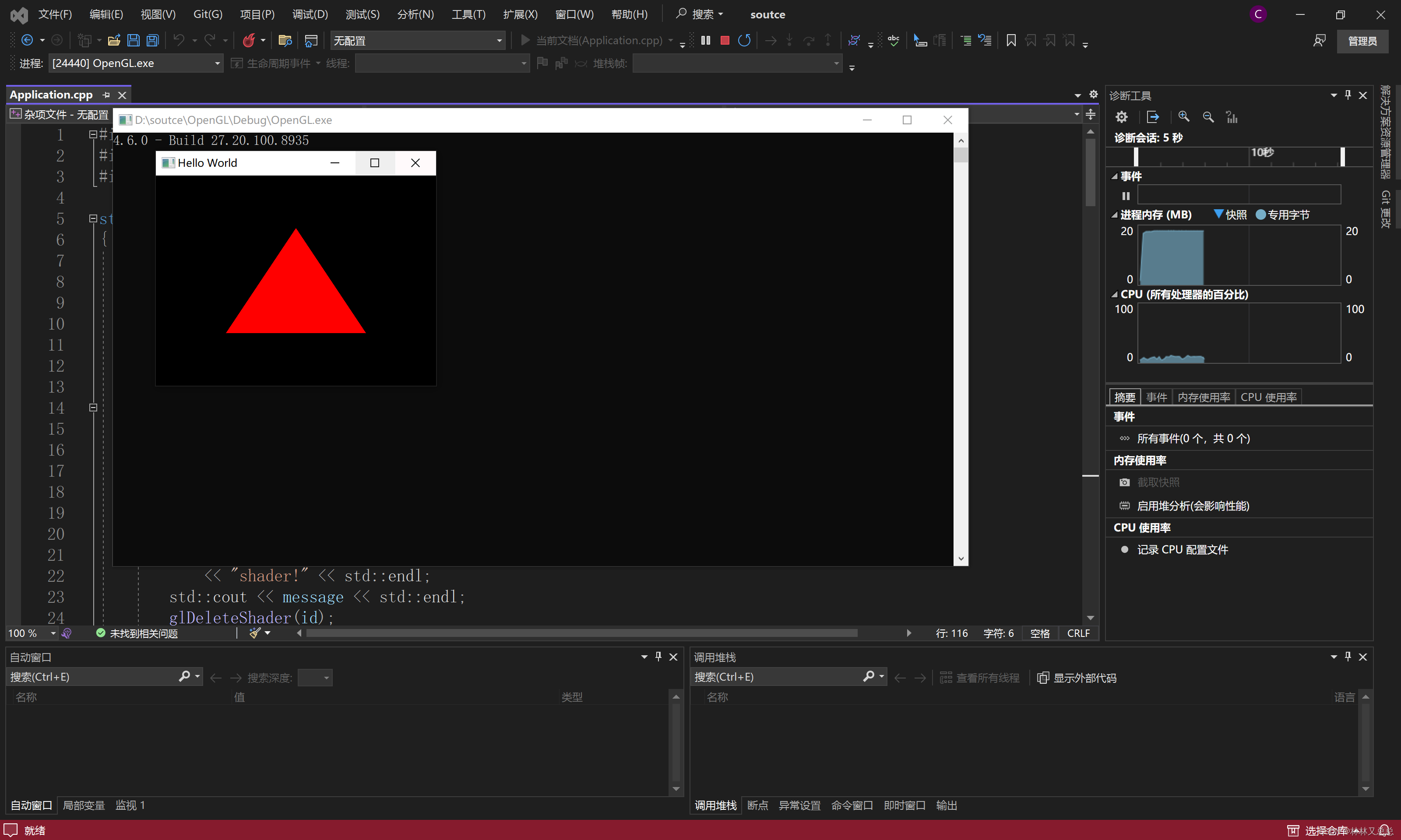
简单着色器编写(下)
函数部分介绍完了,最后来介绍一下main函数中的部分。 std::string vertexShader "#version 330 core\n" "\n" "layout(location0)in vec4 position;" "\n" "void main()\n" "{\n&…...

go并发编程基础
go并发编程 1waitgroup WaitGroup就是等待所有的goroutine全部执行完毕,add方式和Down方法要配套使用 package mainimport ("fmt""sync" )func main() {var wq sync.WaitGroupwq.Add(100) //监控多少个goroutine执行结束for i: 0;i<100;…...

PHP之 导入excel表格时,获取日期时间变成浮点数
读取到的时间 float(0.20833333333333) 原格式 15:00:00 代码 if (Request::isPost()) {$file_url input(upfile); // 本地上传文件地址// 读取文件内容$local_file_url __dir__./../../../public.$file_url;// $spreadsheet new Spreadsheet();// $sheet $spreadsheet-…...

学习 Java 报表技术导入 Maven 依赖出错:jacob 无法下载、jasperreports 依赖错误
发生缘由 最近在做一个可视化项目,用到了 Java 报表技术。在跟着「黑马」课程导入 pom.xml 文件的时候提示下载依赖错误。 com.jacob 包无法下载Failed to read artifact descriptor for com.lowagie:itext:jar:2.1.7.js6 运行环境 电脑系统版本:Win…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
