11 Advanced CNN
文章目录
- GoogLeNet
- Inception Module
- 1x1 Conv
- 计算效果
- 代码实现
- 总结
- ResNet (残差网络)
- 问题引入
- 梯度消失
- 与传统神经网络的比较
- 代码实现
课程来源: 链接
对于前篇中所提到问题,设计出的是一种类似于LeNet5的线性结构,而对于大多数问题,简单的卷积神经网络无法满足需求,因此需要对其进行改进,使之成为一种更加复杂的网络。
GoogLeNet
GoogLeNet包括卷积(Convolution),池化(Pooling)、全连接(Softmax)以及连接(Other)四个部分。
而为了减少代码的冗余,将由以上四个模块所组成的相同的部分,封装成一个类/函数,在GoogLeNet中,这样的部分被称为Inception Module。
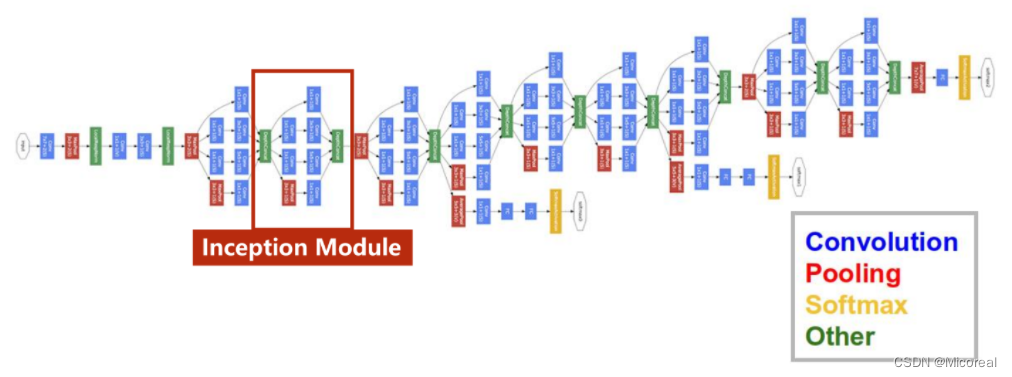
Inception Module
实际上Inception Module以及GoogLeNet自身只是一种基础的网络结构,他的出现是为了解决构造网络时的部分超参数难以确定的问题。
以卷积核大小(kernel_size)为例,虽然无法具体确定某问题中所应使用的卷积核的大小。但是往往可以有几种备选方案,因此在这个过程中,可以利用这样的网络结构,来将所有的备选方案进行计算,并在后续计算过程中增大最佳方案的权重,以此来达到确定超参数以及训练网络的目的。
其中的具体成分可以根据问题进行调整,本文中所详细介绍的Inception Module也仅用作参考。
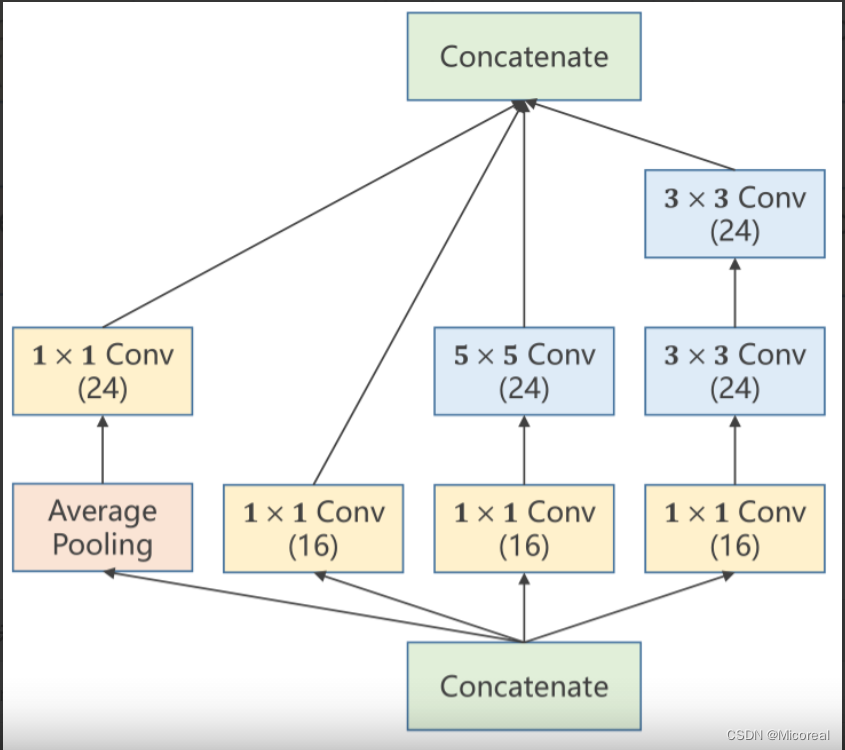

在上述四个路径(四种方法)中,最终的输出图必须仍然保持相同的W(图像宽度)以及H(图像高度),不然无法再次进行拼接传输到下一层模块中。
1x1 Conv
在1×11\times11×1卷积中,每个通道的每个像素需要与卷积中的权重进行计算,得到每个通道的对应输出,再进行求和得到一个单通道的总输出,以达到信息融合的目的。即将同一像素位置的多个通道信息整合在同位置的单通道上。
若需要得到多通道的总输出,以M个通道为例,则需M组的卷积进行计算再进行堆叠拼接。此处和前篇中的多通道卷积是一样的。
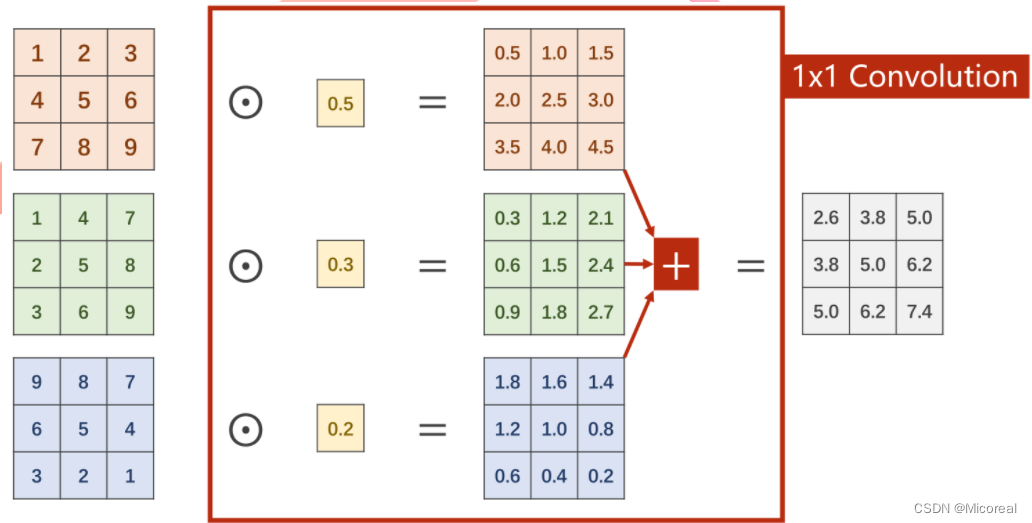
计算效果
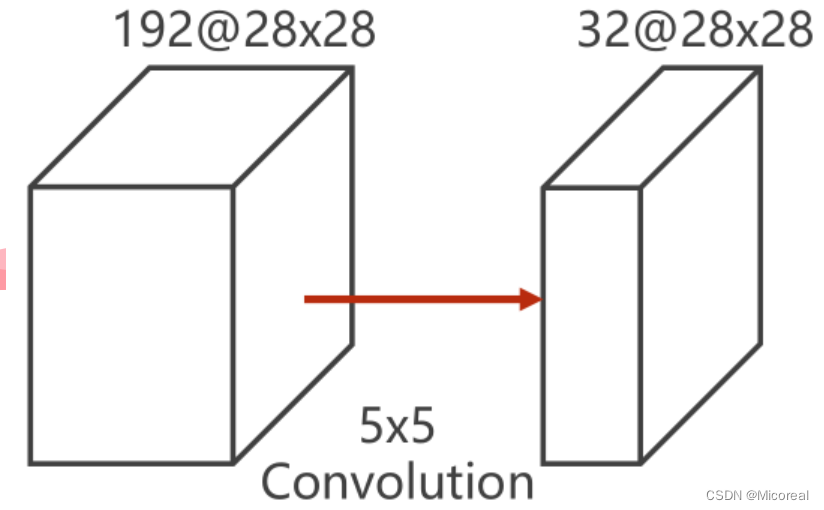
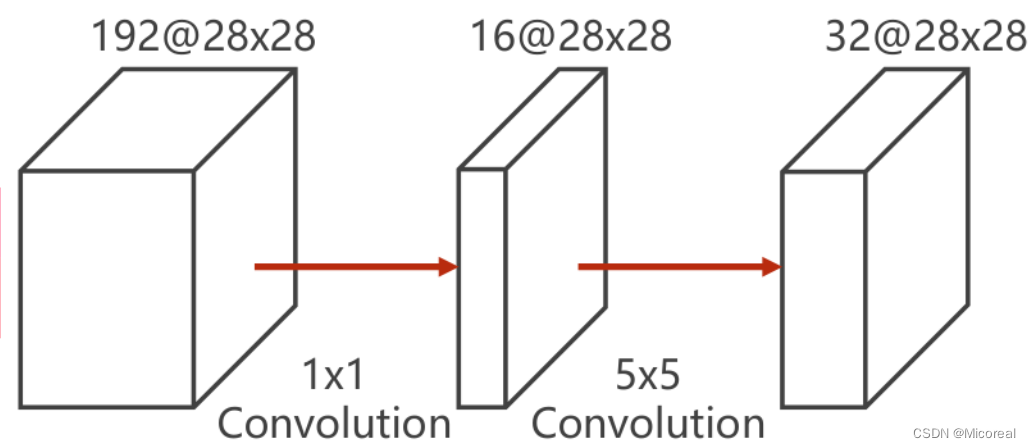
为说明1×11 \times 11×1 卷积的效用,举例原图为192×28×28192 \times 28 \times 28192×28×28的图像,即192个通道,宽高皆为28的图像。输出为32×28×2832 \times 28 \times 2832×28×28的图像,即32个通道,宽高皆为28的图像。为保证前后大小一致,需要使每个像素都在卷积核的中央,即对原图进行padding操作。
若单纯利用一个5×55 \times 55×5的卷积核进行卷积,此时对于每一次卷积,需要计算525^252次,对于每一个通道需要计算28228^2282次卷积,而原图中一共有128个通道,则需要再计算128轮次,此时得到一个单通道的28×2828 \times 2828×28的的输出,因此需要重复上述计算32次,才能得到一个32×28×2832 \times 28 \times 2832×28×28的输出。
即需要计算一亿两千万次以上
52×282×192×32=1204224005^2 \times 28^2 \times 192 \times 32 = 120422400 52×282×192×32=120422400
而对于添加1×11 \times 11×1卷积核的结构,按照上述过程进行计算,仅需要计算一千两百万次左右,整体耗费已经缩减到了原先的十分之一。
12×282×192×16+52×282×16×16=124336481^2 \times 28^2 \times 192 \times 16 + 5^2 \times 28^2 \times 16 \times 16 = 12433648 12×282×192×16+52×282×16×16=12433648
代码实现
为了便于代码说明,此处将原Inception Module模块计算图进行了标注,并对模块中的每一个标注进行单独的代码补充,详解写在代码中
其中主要分为两部分,即对于每一条计算路径上的每一个子模块都包括init定义以及forward计算两部分组成。
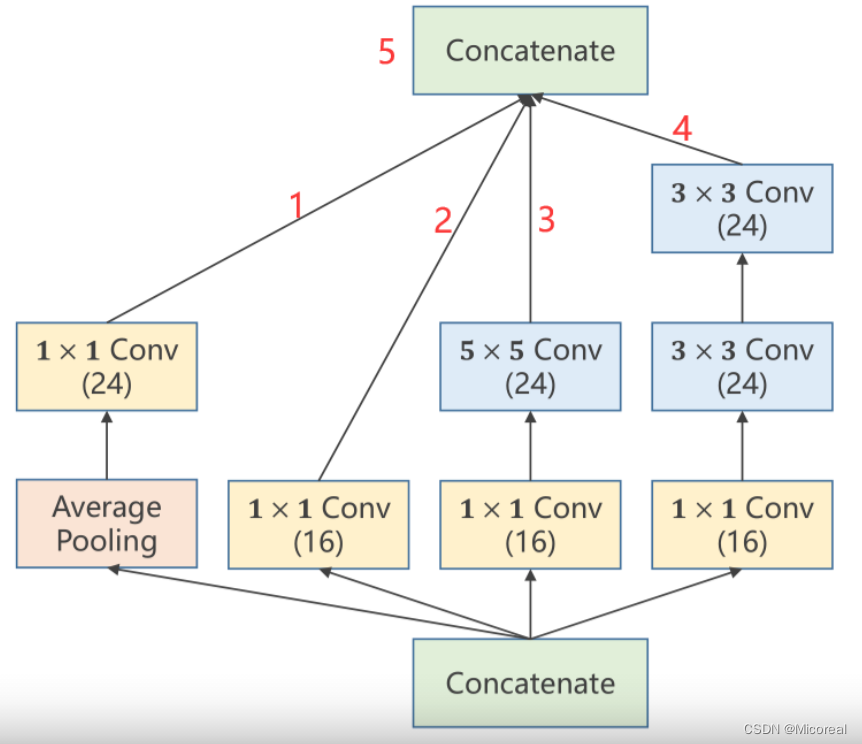
第一部分是由一个均值池化层以及一个输出通道为24的1×11 \times 11×1的卷积构成
#init内定义1x1卷积(输入通道 输出通道 卷积核大小)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)#forward内的方法
#avg_pool2d->均值池化函数 stride以及padding需要手动设置以保持图像的宽度和高度不变
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
#括号内branch_pool的是池化后的结果,括号外的branch_pool是定义的1x1卷积,赋值给对象branch_pool
branch_pool = self.branch_pool(branch_pool)
第二部分是一个输出通道为16的单一的1×11 \times 11×1的卷积
#init中的定义
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)#将元数据直接用于卷积
branch1x1 = self.branch1x1(x)
第三部分包括一个输出通道为16的1×11 \times 11×1的卷积,以及一个输出通道为24的5×55 \times 55×5的卷积
#init定义
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
#设置padding是为了保持图像宽高不变
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)#按照计算图的顺序进行forward嵌套运算
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
第四部分包括一个输出通道为16的1×11 \times 11×1的卷积和两个输出通道为24的3×33 \times 33×3的卷积
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)branch3x3 = self.branch5x5_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
此时经过计算后,会得到各自通道数目不一但图像大小一致的四组图,再利用Concatenate按通道维度方向进行拼接即可得到输出图像
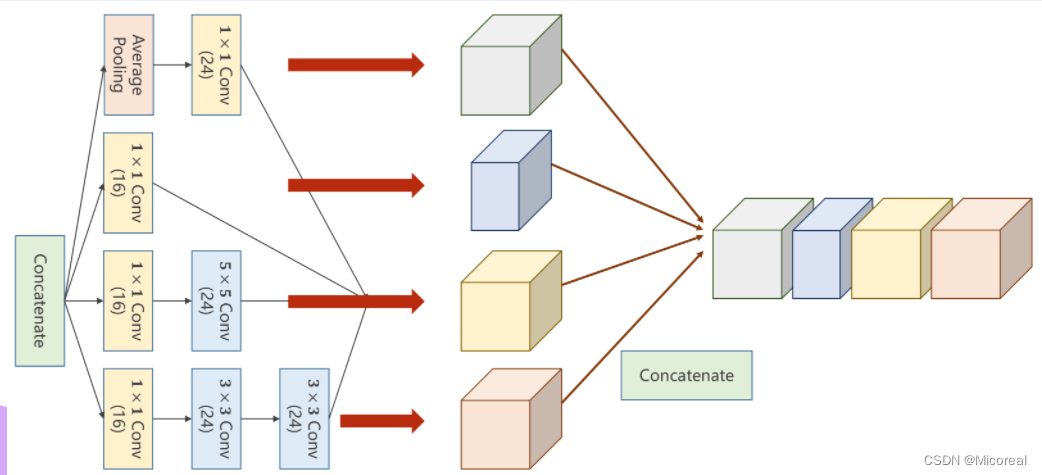
这一过程的步骤如下。
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
#dim=1 意味着按下标为1的维度方向拼接,在图像中即暗指通道(B,C,W,H)
return torch.cat(outputs, dim=1)
代码整理:
class InceptionA(nn.Module):#仅是一个模块,其中的输入通道数并不能够指明def __init__(self, in_channels):super(InceptionA,self).__init__()self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)def forward(self, x):branch1x1 = self.branch1x1(x)branch5x5 = self.branch5x5_1(x)branch5x5 = self.branch5x5_2(branch5x5)branch3x3 = self.branch5x5_1(x)branch3x3 = self.branch3x3_2(branch3x3)branch3x3 = self.branch3x3_3(branch3x3)branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)branch_pool = self.branch_pool(branch_pool)outputs = [branch1x1, branch5x5, branch3x3, branch_pool]return torch.cat(outputs, dim=1)class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 10, kernel_size=5)# 在Inception的定义中,拼接后的输出通道数为24+16+24+24=88个self.conv2 = nn.Conv2d(88, 20, kernel_size=5)self.incep1 = InceptionA(in_channels=10)self.incep2 = InceptionA(in_channels=20)self.mp = nn.MaxPool2d(2)#关于1408:#每次卷积核是5x5,则卷积后原28x28的图像变为24x24的#再经过最大池化,变为12x12的#以此类推最终得到4x4的图像,又inception输出通道88,则转为一维后为88x4x4=1408个self.fc = nn.Linear(1408, 10)def forward(self,x):in_size = x.size(0)x = F.relu(self.mp(self.conv1(x)))x = self.incep1(x)x = F.relu(self.mp(self.conv2(x)))x = self.incep2(x)x = x.view(in_size, -1)x = self.fc(x)return x
总结
GooLeNet在于强调去把网络做得更加深层,借此使网络变得更为复杂。
ResNet (残差网络)
问题引入
若将某个大小固定的卷积核进行反复迭代,会不会得到更好的结果。
但事实上,以CIFAR-10为例,对于3×33 \times 33×3的卷积而言,20层的训练效果要优于56层。由图中可以明显看出,在训练集以及测试集中,20层的误差是更小的。
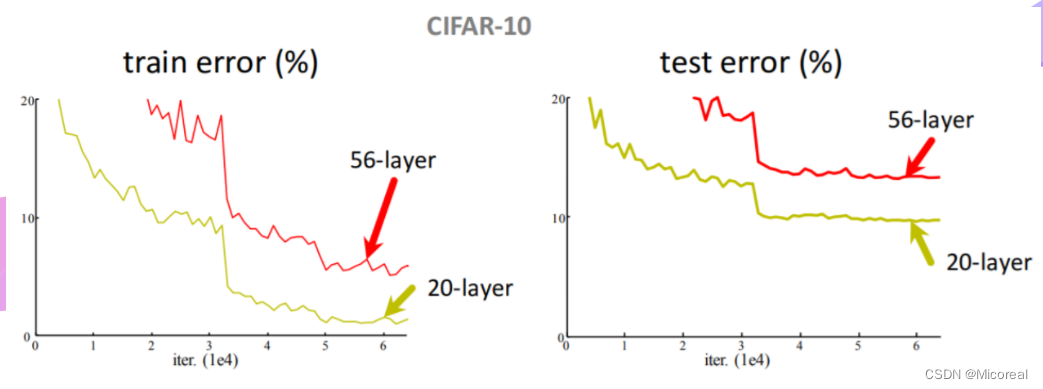
其中最可能的原因是梯度消失问题。
梯度消失
由于在梯度计算的过程中是用的反向传播,所以需要利用链式法则来进行梯度计算,是一个累乘的过程。若每一个地方梯度都是小于1的,即
∂cost∂ω<1\frac{\partial cost}{\partial \omega} < 1 ∂ω∂cost<1
,则累乘之后的总结果应趋近于0,即
∂Cost∂Ω→0\frac{\partial Cost}{\partial \Omega} \to 0 ∂Ω∂Cost→0
由原先权重更新公式
ω=ω−α∂cost∂ω\omega = \omega - \alpha \frac{\partial cost}{\partial \omega} ω=ω−α∂ω∂cost
可知,∂cost∂ω\frac{\partial cost}{\partial \omega}∂ω∂cost趋近于0,则ω\omegaω不会再进行进一步的更新。由于深度学习的网络层数较多,为了解决梯度消失问题,从而产生了ResNet。
与传统神经网络的比较
在Residual Net中引入了跳链接,即让输入在N(一般N=2N=2N=2)层连接后并入第N层的输出,实现如图所示的
H(x)=F(x)+xH(x) = F(x) + x H(x)=F(x)+x
之后再进行relu激活,以此来得到输出。
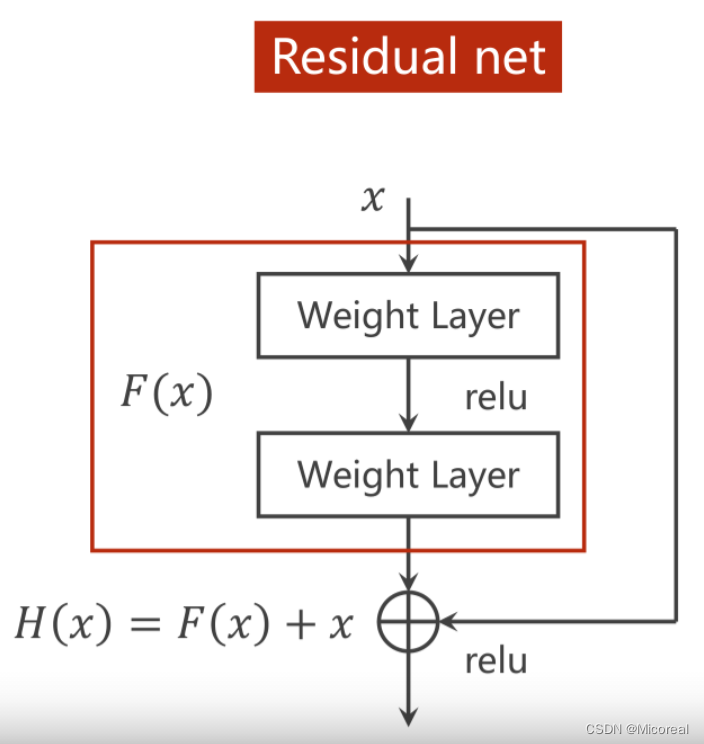
在这样的结构中,以上图为例,如果要进行H(x)H(x)H(x)对xxx的求导,则会有
∂H(x)∂x=∂F(x)∂x+1\frac{\partial H(x)}{\partial x} = \frac{\partial F(x)}{\partial x} + 1 ∂x∂H(x)=∂x∂F(x)+1
即,若存在梯度消失现象,即存在某一层网络中的∂F(x)∂x→0\frac{\partial F(x)}{\partial x} \to 0∂x∂F(x)→0,由于上式存在,则会使得在方向传播过程中,传播的梯度会保持在1左右,即∂H(x)∂x→1\frac{\partial H(x)}{\partial x} \to 1∂x∂H(x)→1.如此,离输入较近的层也可以得到充分的训练。
代码实现
由于在ResNet中,跳链接需要实现一个权重层结果与输入相加的操作,则需要保证权重层的输出结果,与输入的维度是相同的。即等宽等高等通道数。

上图中标问号的红色块是残差块,其输入以及输出层的大小应当保持一致。
class RsidualBlock(nn.Module):def __init__(self, in_channels):super(RsidualBlock, self).__init__()#保持输出和输入一致self.channels = in_channelsself.conv1 = nn.Conv2d(in_channels, in_channels, kernel_size=3, padding=1)self.conv2 = nn.Conv2d(in_channels, in_channels, kernel_size=3, padding=1)def forward(self, x):y = F.relu(self.conv1(x))#第二层先求和再激活y = self.conv2(y)return F.relu(x+y)
结构代码:
class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 16, kernel_size=5)self.conv2 = nn.Conv2d(16, 32, kernel_size=5)self.mp - nn.MaxPool2d(2)self.rblock1 = ResiduleBlock(in_channels=16)self.rblock2 = ResidualBlock(in_channels=32)self.fc = nn.Linear(512, 10)def forward(self,x):in_size = x.size(0)x = self.mp(F.relu(self.conv1(x)))x = self.rblock1(x)x = self.mp(F.relu(self.conv2(x)))x = self.rblock2(x)x = x.view(in_size, -1)x = self.fc(x)return x
相关文章:

11 Advanced CNN
文章目录GoogLeNetInception Module1x1 Conv计算效果代码实现总结ResNet (残差网络)问题引入梯度消失与传统神经网络的比较代码实现课程来源: 链接对于前篇中所提到问题,设计出的是一种类似于LeNet5的线性结构,而对于大多数问题,简…...

亿级高并发电商项目---万达商城项目搭建(二)
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...

UML术语标准和分类
一、UML术语标准 1.中文UML术语标准 中国软件行业协会(CSIA)与日本UML建模推进协会(UMTP)共同在中国推动的UML专家认证,两个协会共同颁发认证证书、两国互认,CSIA与UMTP共同推出了UML中文术语…...

LeetCode 刷题系列 -- 151. 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。注意:输入字符串 s中可能会存在前导空格、尾随空格或…...
二十二、Gtk4-ListView
GTK 4添加了新的列表对象GtkListView、GtkGridView和GtkColumnView。这个新特性在Gtk API参考—列表小构件概述中有描述。 GTK 4还有其他实现列表的方法。它们是GtkListBox和GtkTreeView,它们是从GTK 3接管的。在Gtk开发博客中有一篇关于Matthias Clasen所写的列表…...
ASP.NET Core3.1实战教程---基于Jquery单文件上传
这个必须记录一下费劲啊!废了我2天的时间,昔日的net快速已经没落....就文件上传都这么费劲。 先说下要求(在线apk文件上传实现手机端整包更新): 1、为了简化需求文件上传和数据提交分开执行 2、选完文件后按钮变成上…...
10 卷积神经网络CNN(基础篇)
文章目录全连接CNN过程卷积过程下采样过程全连接层卷积原理单通道卷积多通道卷积改进多通道总结以及课程代码卷积改进PaddingStride下采样过程大池化层(Max Pooling)简单卷积神经网络的实现课程代码本篇课程来源: 链接部分文本来源参考&#…...

Windows下LuaBridge2.8的环境配置及简单应用
Windows下LuaBridge2.8的环境配置及简单应用 LuaBridge2.8下载链接: https://github.com/vinniefalco/LuaBridge/tags 关于Lua的环境配置可参考以下链接(这里不做简述): https://ufgnix0802.blog.csdn.net/article/details/125341…...

每天10个前端小知识 【Day 10】
前端面试基础知识题 1. es5 中的类和es6中的class有什么区别? 在es5中主要是通过构造函数方式和原型方式来定义一个类,在es6中我们可以通过class来定义类。 class类必须new调用,不能直接执行。 class类执行的话会报错,而es5中…...

【LeetCode】1223. 掷骰子模拟
1223. 掷骰子模拟 题目描述 有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。 不过我们在使用它时有个约束,就是使得投掷骰子时,连续 掷出数字 i 的次数不能超过 rollMax[i](i 从 1 开始编号)。 现在,…...

SPSS数据分析软件的安装与介绍(附网盘链接)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
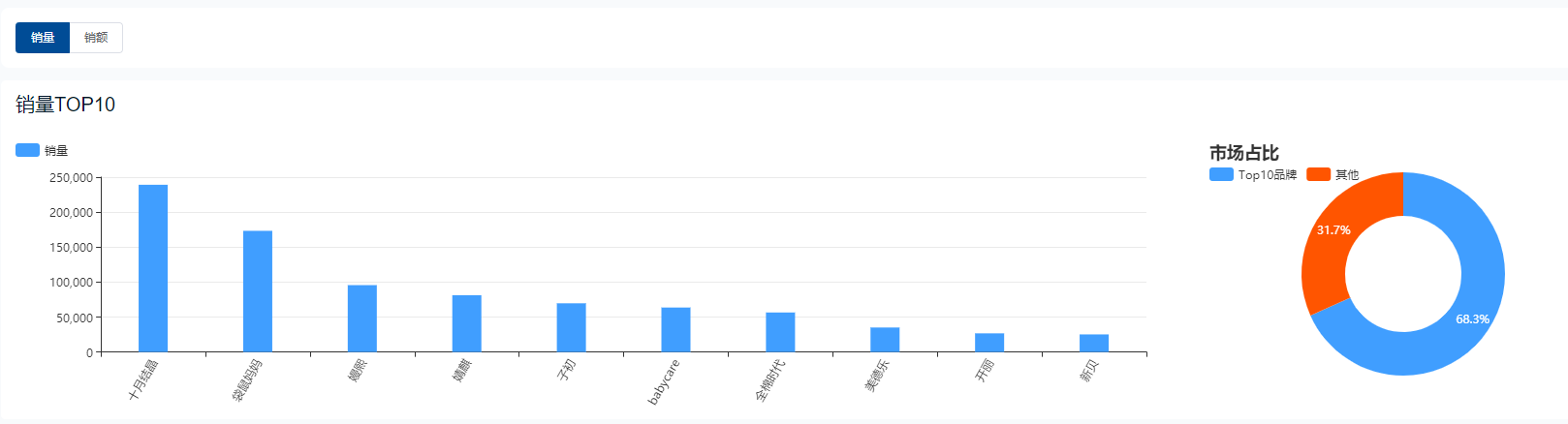
2022年38女神节大促美妆、珠宝、母婴、保健电商数据回顾
近期,我们陆续接收到了品牌商家朋友们对于2022年女神节大促期间部分品类的数据需求,希望能对今年的大促活动有一个更宏观的认知、更精准的预测,从而拿到更好的数据效果。 为此,在距离大促开启一个月的备货阶段,鲸参谋决…...

Java笔记-线程同步
目录线程的同步---以三个窗口售票100张为例方式一:同步代码块方式二:同步方法使用同步机制的作用:线程的同步—以三个窗口售票100张为例 (1)问题:卖票的过程出现重票和错票 (2)原因…...
通过python 调用OpenAI api_key提交问题解答
通过python 调用OpenAI api_key提交问题解答✨可以通过网页版的jupyter notebook调用,也可以通过spyder窗口等IDE窗口. 🌼通过python 调用OpenAI api_key接口,可以避免国内网页不能访问的问题。前提是需要自己已经注册了OpenAI帐号ÿ…...
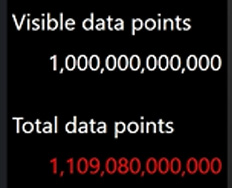
图表控件LightningChart .NET再破世界纪录,支持实时可视化 1 万亿个数据点
LightningChart.NET SDK 是一款高性能数据可视化插件工具,由数据可视化软件组件和工具类组成,可支持基于 Windows 的用户界面框架(Windows Presentation Foundation)、Windows 通用应用平台(Universal Windows Platfor…...
什么是响应性?
响应性: 这个术语在今天的各种编程讨论中经常出现,但人们说它的时候究竟是想表达什么意思呢?本质上,响应性是一种可以使我们声明式地处理变化的编程范式。一个经常被拿来当作典型例子的用例即是 Excel 表格: 这里单元…...
黑马】后台管理176-183
一、新建订单管理的分支二、创建一个订单管理的vue文件进行组件页面的路由配置import Order from ../components/order/Order.vue{path:/orders,component:Order},注意上面的components不要忘记少加一个s!三,获取后台数据面包屑导航粘贴过来文本输入框&a…...
通俗易懂详细教程)
Typescript - 类型守卫(typeof / in / instanceof / 自定义类型保护的类型谓词)通俗易懂详细教程
前言 类型守卫用于获取变量类型信息,通常使用在条件块语句中。类型守卫是返回布尔值的常规函数,接受一个类型并告诉 TypeScript 是否可以缩小到更具体的类型。类型守卫具有唯一的属性,可以确保测试的值返回的是布尔值类型。 TypeScript 使用了…...

6.8 左特征向量
特征值很复杂,除了普通的特征向量外,还有左特征向量和广义特征向量。先说说比较容易的左特征向量吧。它是这样定义的,AAA是一个矩阵,λ\lambdaλ是它的一个特征值,下面的向量yyy就是矩阵关于特征值的左特征向量left ei…...
10个自动化测试框架,测试工程师用起来
软件行业正迈向自主、快速、高效的未来。为了跟上这个高速前进的生态系统的步伐,必须加快应用程序的交付时间,但不能以牺牲质量为代价。快速实现质量是必要的,因此质量保证得到了很多关注。为了满足卓越的质量和更快的上市时间的需求…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
