每日一题:leetcode 1267 统计参与通信的服务器
这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。
如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。
请你统计并返回能够与至少一台其他服务器进行通信的服务器的数量。
示例 1:
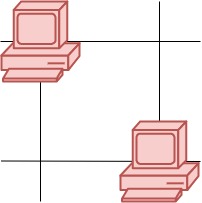
输入:grid = [[1,0],[0,1]] 输出:0 解释:没有一台服务器能与其他服务器进行通信。
示例 2:
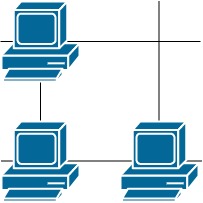
输入:grid = [[1,0],[1,1]] 输出:3 解释:所有这些服务器都至少可以与一台别的服务器进行通信。
示例 3:
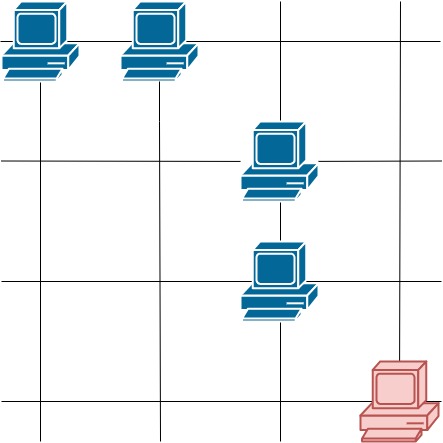
输入:grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]] 输出:4 解释:第一行的两台服务器互相通信,第三列的两台服务器互相通信,但右下角的服务器无法与其他服务器通信。
提示:
m == grid.lengthn == grid[i].length1 <= m <= 2501 <= n <= 250grid[i][j] == 0 or 1
思路:
暴力遍历。。。。(我这种肯定不是最优的)
先按行遍历,如果出现第一个,先记录位置,然后看看有没有第二个的出现。
ac code:
class Solution {public int countServers(int[][] grid) {int ans = 0;int n = grid.length;int m = grid[0].length;boolean[][] vis = new boolean[n][m];for (int i = 0;i<n;i++) {int flag = 0;int firstX = -1;int firstY = -1;for (int j =0;j<m;j++) {if (grid[i][j] == 1) {if (flag > 1) {ans += 1;vis[i][j] = true;} else if (flag == 1) {ans += 2;vis[i][j] = true;vis[firstX][firstY] = true;} else {firstX = i;firstY = j;}flag += 1;}}}for (int i=0;i<m;i++) {int flag = 0;int firstX = -1;int firstY = -1;for (int j=0;j<n;j++) {if (grid[j][i] == 1) {if (flag > 1) {ans += (vis[j][i] ? 0 : 1);vis[j][i] = true;} else if (flag == 1) {ans += (vis[j][i] ? 0 : 1);ans += (vis[firstX][firstY] ? 0 : 1);vis[j][i] = true;vis[firstX][firstY] = true;} else {firstX = j;firstY = i;}flag += 1;}}}return ans;}
}还有更优的,比如可以通过hashmap去记录行列是否出现,或者是通过一维数组+一个变量去记录,放一个更优的解法。
class Solution:def countServers(self, grid: List[List[int]]) -> int:m,n=len(grid),len(grid[0])col_alone=[-1]*nans=0for i in range(m):row_alone=-1for j in range(n):if grid[i][j]==0:continueif row_alone==-1 and col_alone[j]==-1:##同行同列没有服务器row_alone=jcol_alone[j]=ielse:if row_alone>=0:ans+=1col_alone[row_alone]=-2ans+=(col_alone[j]>=0)+1row_alone=-2col_alone[j]=-2return ans
相关文章:

每日一题:leetcode 1267 统计参与通信的服务器
这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。 请你统计并返回能够与至少一台其他服务…...
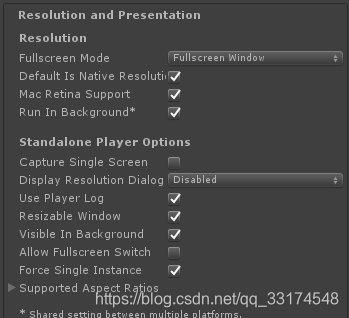
Unity打包Windows程序,概率性出现无法全屏或分辨率不匹配
排除代码和Resolution and Presentation面板设置问题 如果程序还是不能按照预期的分辨率运行,应该是系统注册表记录了对应的设置。 解决方案: 打开注册表,使用快捷键“Win” "R"组合快捷键。在打开后面键入命令:Rege…...

消息中间件 介绍
MQ简介 MQ,Message queue,消息队列,就是指保存消息的一个容器。具体的定义这里就不类似于数据库、缓存等,用来保存数据的。当然,与数据库、缓存等产品比较,也有自己一些特点,具体的特点后文会做详细的介绍。 现在常用…...

JAVA-字符串长度
给定一行长度不超过 100 的非空字符串,请你求出它的具体长度。 输入格式 输入一行,表示一个字符串。注意字符串中可能包含空格。 输出格式 输出一个整数,表示它的长度。 数据范围 1≤字符串长度≤100 字符串末尾无回车 输入样例: …...
[oneAPI] 基于BERT预训练模型的SWAG问答任务
[oneAPI] 基于BERT预训练模型的SWAG问答任务 基于Intel DevCloud for oneAPI下的Intel Optimization for PyTorch基于BERT预训练模型的SWAG问答任务数据集下载和描述数据集构建问答选择模型训练 结果参考资料 比赛:https://marketing.csdn.net/p/f3e44fbfe46c465f4d…...
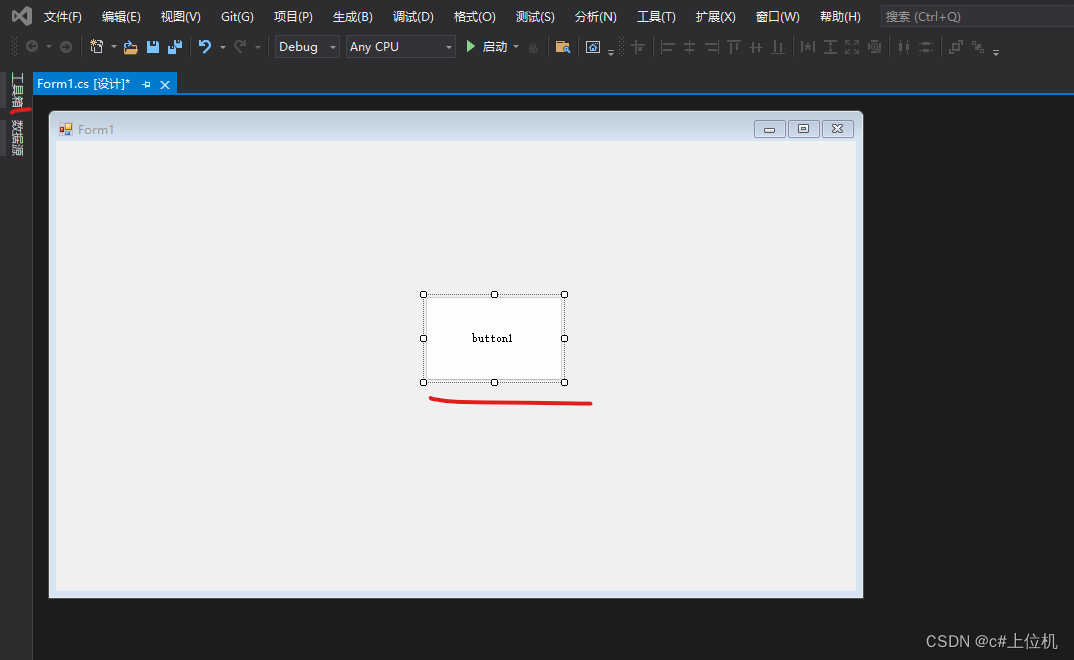
如何为winform控件注册事件
有很多winform的初学者不知道如何为winform注册的事件代码,本篇博文就是以button控件为例子,为winform注册单击事件,如下: 1、新建一个winform 以visual studio 2019 社区版为例子,新建一个winform程序,如下: 关于visual studio 2019 社区版下载方式点击这里:手把手教…...

【LeetCode-面试经典150题-day15】
目录 104.二叉树的最大深度 100.相同的树 226.翻转二叉树 101.对称二叉树 105.从前序与中序遍历序列构造二叉树 106.从中序与后序遍历序列构造二叉树 117.填充每个节点的下一个右侧节点指针Ⅱ 104.二叉树的最大深度 题意: 给定一个二叉树 root ,返回其…...

git查看和修改项目远程仓库地址
git查看和修改项目远程仓库地址 一、背景 项目代码仓库迁移,需要本地更新远程仓库地址,进行代码同步与提交。 二、查看项目的远程仓库地址 # 查看远程地址 git remote -v # 查看远程仓库信息(分支、地址等) git remote show origin三、修…...
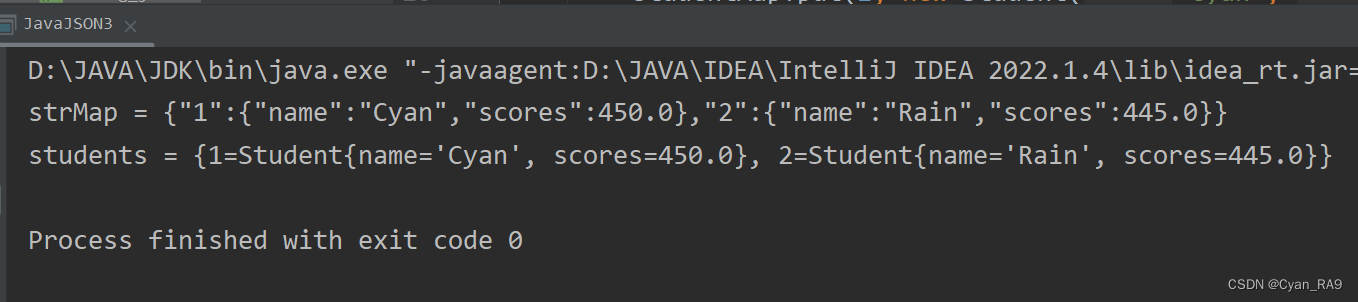
JavaWeb 速通JSON
目录 一、JSON快速入门 1.基本介绍 : 2.定义格式 : 3.入门案例 : 二、JSON对象和字符串的相互转换 1.常用方法 : 2.应用实例 : 3.使用细节 : 三、JSON在Java中的使用 1.基本说明 : 2.应用场景 : 2.1 JSON <---> JavaBean 2.2 JSON <---> List 2.3 JSON …...
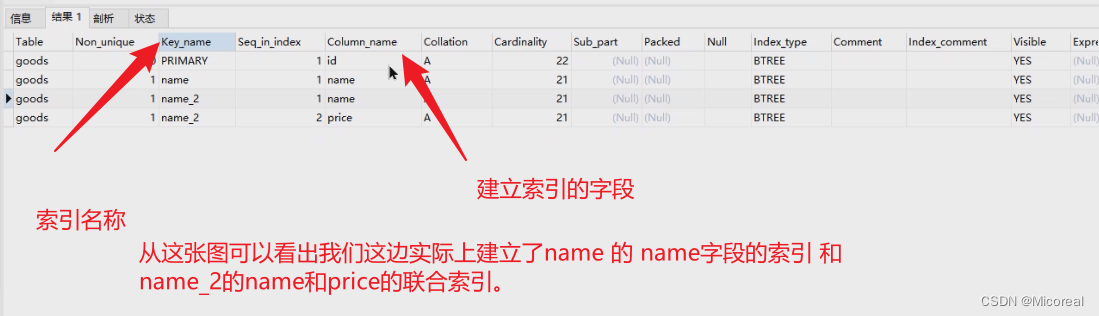
20 MySQL(下)
文章目录 视图视图是什么定义视图查看视图删除视图视图的作用 事务事务的使用 索引查询索引创建索引删除索引聚集索引和非聚集索引影响 账户管理(了解非DBA)授予权限 与 账户的相关操作 MySQL的主从配置 视图 视图是什么 通俗的讲,视图就是…...
测试圈的网红工具:Jmeter到底难在哪里?!
雨果的公司最近推出了一款在线购物应用,吸引了大量用户。然而随着用户数量的增加,应用的性能开始出现问题。用户抱怨说购物过程中页面加载缓慢,甚至有时候无法完成订单,小欧作为负责人员迫切需要找到解决方案。 在学习JMeter之前…...
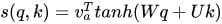
深度学习10:Attention 机制
目录 Attention 的本质是什么 Attention 的3大优点 Attention 的原理 Attention 的 N 种类型 Attention 的本质是什么 Attention(注意力)机制如果浅层的理解,跟他的名字非常匹配。他的核心逻辑就是「从关注全部到关注重点」。 Attention…...
)
简单着色器编写(中下)
这篇我们来介绍另一部分函数。 static unsigned int CreateShader(const std::string& vertexShader, const std::string& fragmentShader) {unsigned int program glCreateProgram();unsigned int vs CompileShader(GL_VERTEX_SHADER,vertexShader);unsigned int f…...
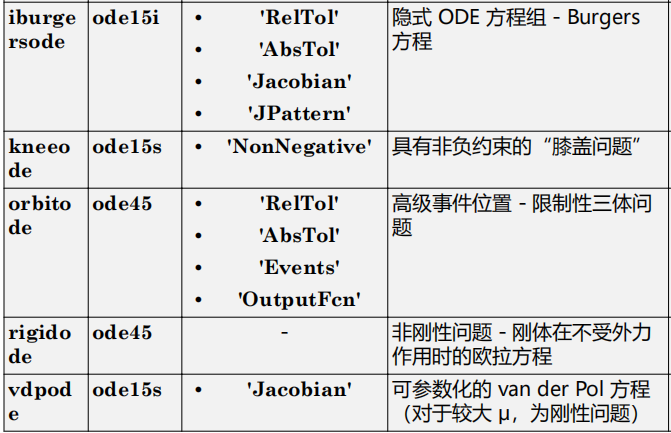
matlab使用教程(24)—常微分方程(ODE)求解器
1.常微分方程 常微分方程 (ODE) 包含与一个自变量 t(通常称为时间)相关的因变量 y 的一个或多个导数。此处用于表示 y 关于 t 的导数的表示法对于一阶导数为 y ′ ,对于二阶导数为 y ′′,依此类推。ODE 的阶数等于 y 在方程中…...

企业级数据共享规模化模式
数据共享正在成为企业数据战略的重要元素。对于公司而言,Amazon Data Exchange 这样的亚马逊云科技服务提供了与其他公司共享增值数据或从这些数据获利的途径。一些企业希望有一个数据共享平台,他们可以在该平台上建立协作和战略方法,在封闭、…...
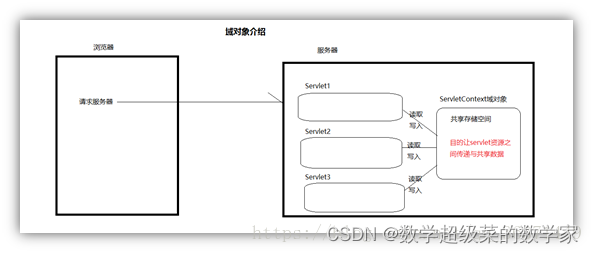
Web服务器-Tomcat详细原理与实现
Tomcat 安装与使用 :MAC 安装配置使用Tomcat - 掘金 安装后本计算机就相当于一台服务器了!!! 方式一:使用本地安装的Tomcat 1、将项目文件移动到Tomcat的webapps目录下。 2、启动Tomcat 3、在浏览器输入想要加载的…...
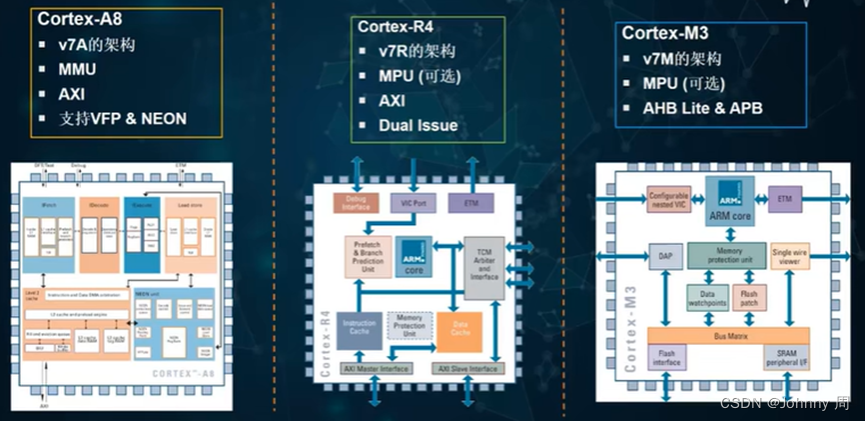
ARM处理器核心概述
一、基于ARM处理器的嵌入式系统 ARM核深度嵌入SOC中,通过JTAG口进行外部调试。计通常既有外部内存又有内部内存,从而支持不通的内存宽度、速度和大小。一般会包含一个中断控制器。可能包含一些Primece外设,需要从ARM公司取得授权。总线使用A…...
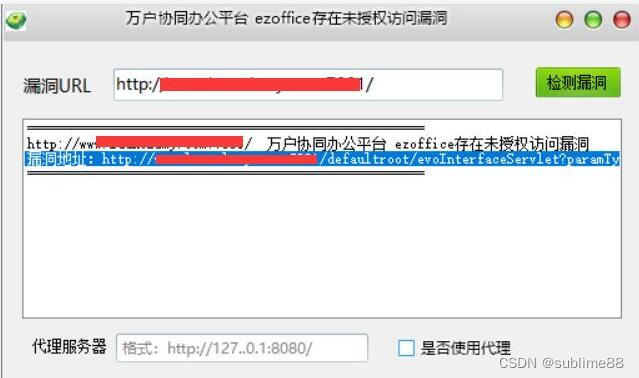
万户协同办公平台 ezoffice存在未授权访问漏洞 附POC
文章目录 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC1. 万户协同办公平台 ezoffice简介2.漏洞描述3.影响版本4.fofa查询语句5.漏洞复现6.POC&EXP7.整改意见8.往期回顾 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC 免责声明:请勿利用文章内的相…...
使用ctcloss训练矩阵生成目标字符串
首先我们需要明确 c t c l o s s ctcloss ctcloss是用来做什么的。比如说要生成的目标字符串长度为 l l l,而这个字符串包含 s s s个字符,字符串允许的最大长度为 L L L,这里认为一个位置是一个时间步,就是一拍,记为 T…...
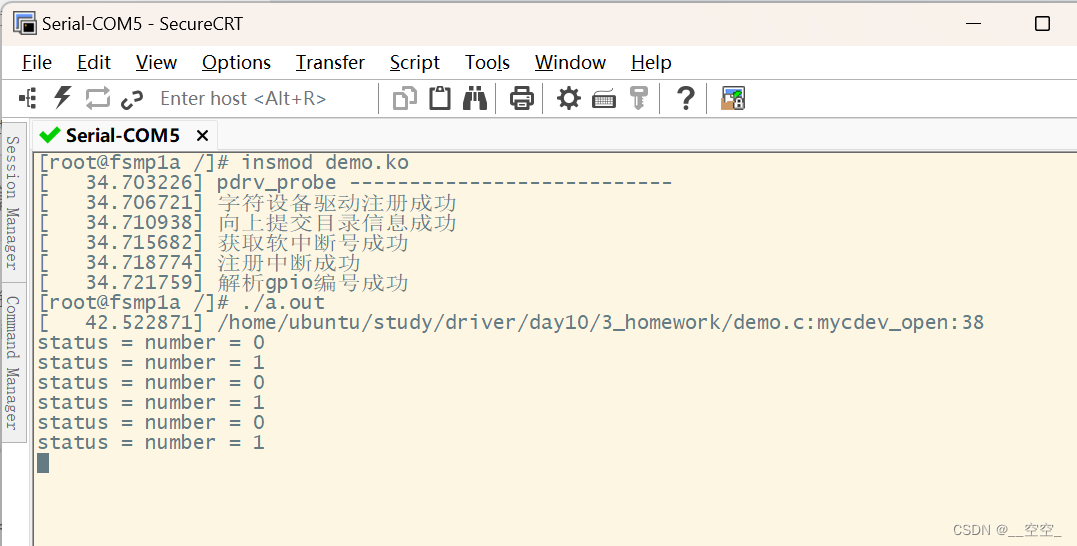
驱动 - 20230829
练习 基于platform实现 在根节点下,增加设备树 myplatform {compatible"hqyj,myplatform";interrupts-extended<&gpiof 9 0>, <&gpiof 7 0>, <&gpiof 8 0>;led1-gpio<&gpioe 10 0>;reg<0x12345678 59>;}…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
