【数据结构与算法篇】手撕八大排序算法之快排的非递归实现及递归版本优化(三路划分)

👻内容专栏: 《数据结构与算法篇》
🐨本文概括: 利用数据结构栈(Stack)来模拟递归,实现快排的非递归版本;递归版本测试OJ题时,有大量重复元素样例不能通过,导致性能下降,优化快速排序通过将数组划分为三个区域,可以更有效地处理重复元素。
🐼本文作者: 阿四啊
🐸发布时间:2023.8.28
快速排序(非递归)
1.为什么要学习非递归版本?
前面我们使用了三个版本实现快速排序,但都是属于递归类型算法,函数调用会建立函数栈帧,递归深度取决于函数调用的次数。栈空间内存有限,在处理大规模数据集时,递归深度的增加可能导致栈溢出的情况,所以在我们学会了递归版本之后,需要继续强化学习非递归版本,利用之前学习的数据结构栈(Stack)来模拟实现。
2.基本思想
我们知道,我们在写递归版本的时候,快速排序主要处理的是数组的不同区间,将问题分解为较小的子问题并在每个子问题上递归地应用相同的排序算法来完成排序。

那么我们如何使用栈(Stack)来模拟实现呢?
核心思想是使用一个栈来存储待排序的子数组的起始和结束下标。在每次循环中,从栈中弹出一个子数组并执行分区操作(根据基准值(
key),划分区间,这一步骤即递归版本写的Partition函数),选然后根据分区结果将未处理的左右子数组的下标压入栈中,直到栈为空为止。
3.算法分析
👇①:
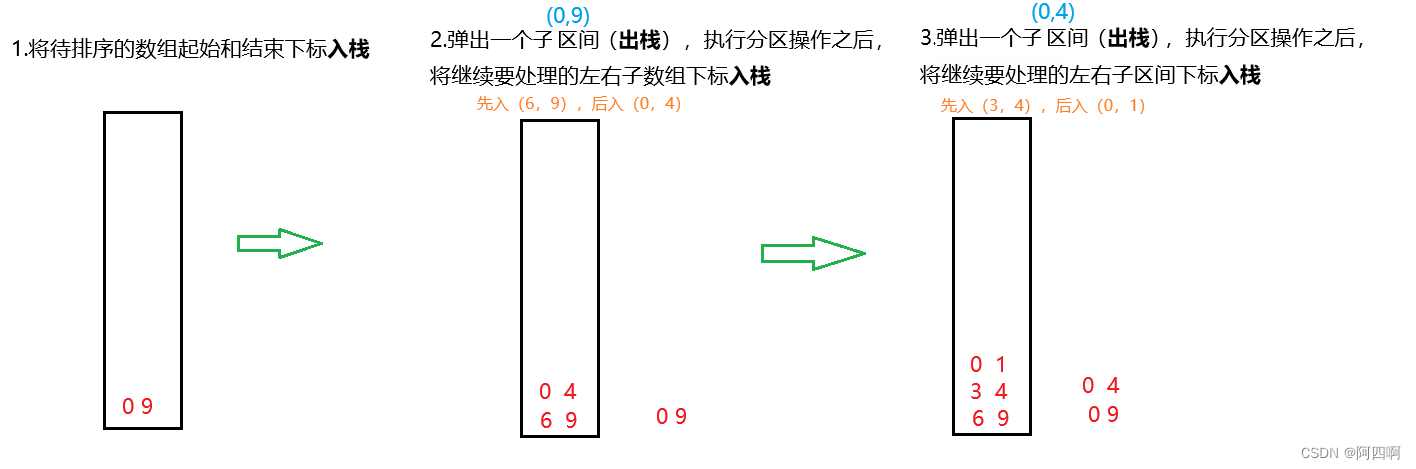
👇②:
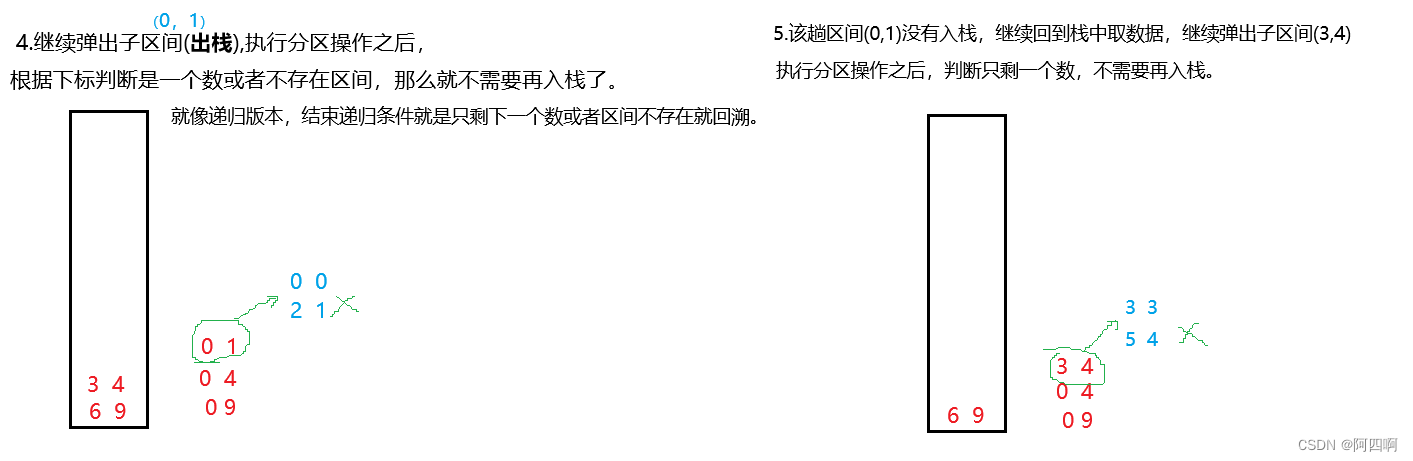
👇③:继续重复以上步骤,直到栈中的数据为空。
4.代码实现
因为涉及到使用栈,而本篇数据结构基于C语言讲解,所以讲自己实现的栈的文件源代码也顺便放在这。
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
//hoare版本
int Partition1(int* a, int left, int right)
{int keyi = left;while (left < right){//注意: 要加上left < right 否则会出现越界//若不判断等于基准值,也会出现死循环的情况//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}void QuicksortNonR(int* a, int begin, int end)
{Stack st;StackInit(&st);//注意栈的顺序是后进先出,需要倒着放进去,正着拿出来//将排序数组的起始和末端下标入栈StackPush(&st, end);StackPush(&st, begin);//栈不为空一直循环while (!StackEmpty(&st)){//弹出子区间(左右两个下标)int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);//执行分区操作int keyi = Partition1(a, left, right);//[left,keyi - 1] keyi [keyi + 1, right]//注意只剩一个数或区间不存在则停止入栈if (keyi + 1 < right){StackPush(&st,right);StackPush(&st,keyi + 1);}if (left < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, left);}}}
void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}
int main()
{int a[] = { 9,6,7,1,4,5,5,2,10,1,6,3,7 };QuicksortNonR(a, 0, sizeof a / sizeof(int) - 1);PrintArray(a, sizeof a / sizeof(int));
}
栈
相关函数声明:
#pragma once
#include <stdio.h>
#include <stdbool.h>
#include <assert.h>
#include <stdlib.h>
typedef int DataType;
typedef struct Stack
{DataType* a;int top;int capacity;}Stack;//栈的初始化
void StackInit(Stack* pst);
//入栈
void StackPush(Stack* pst,DataType x);
//出栈
void StackPop(Stack* pst);
//栈的销毁
bool StackEmpty(Stack* pst);
//获取栈顶元素
DataType StackTop(Stack* pst);
//获取栈元素个数
int StackSize(Stack* pst);
//栈的销毁
void StackDestroy(Stack* pst);
相关函数实现:
#define _CRT_SECURE_NO_WARNINGS
#include "stack.h"
//栈的初始化
void StackInit(Stack* pst)
{assert(pst);pst->a = NULL;//pst->top = -1;//栈顶元素的位置pst->top = 0;//栈顶元素的下一个位置pst->capacity = 0;
}
//入栈
void StackPush(Stack* pst,DataType x)
{if (pst->top == pst->capacity){int newCapacity = pst->capacity == 0 ? 4 : (pst->capacity) * 2;DataType* tmp = (DataType*)realloc(pst->a, sizeof(DataType) * newCapacity);if (tmp == NULL){perror("realloc fail\n");return;}else{pst->a = tmp;pst->capacity = newCapacity;}}pst->a[pst->top++] = x;
}
//出栈
void StackPop(Stack* pst)
{assert(pst);pst->top--;
}
//判断栈是否为空
bool StackEmpty(Stack* pst)
{assert(pst);return pst->top == 0;
}
//获取栈顶元素
DataType StackTop(Stack* pst)
{return pst->a[pst->top - 1];
}
//获取栈元素个数
int StackSize(Stack* pst)
{return pst->top;
}
//栈的销毁
void StackDestroy(Stack* pst)
{assert(pst);free(pst->a);pst->a = NULL;pst->top = pst->capacity = 0;
}
总结
时间复杂度:O(N*logN)
空间复杂度:O(logN)
⚠️注意:尽管使用栈实现了递归过程,但栈的使用本质上是在模拟递归调用栈。这种方法可以避免递归深度过大导致栈溢出的问题,并且在一些情况下比递归版本更有效。
递归版本优化(三路划分)
1.缺陷问题:
下面给出一道力扣OJ题:👉传送链接:912.排序数组
题目要求就是给定一些数据,将乱序的数组排列为升序。我们用希尔排序、归并排序、堆排序……一般效率较高的都可以跑过,但是唯独快排用递归、非递归都不能跑过!就很离谱,因为快排有名,也就是这题故意针对快排,下面利用写出的递归版本的快排去跑这个OJ。
/*** Note: The returned array must be malloced, assume caller calls free().*/void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//三数取中
int GetMidIndax(int* a,int left, int right)
{int mid = left + (rand() % (right - left));if (a[mid] > a[left]){if (a[right] > a[mid]) return mid;else if (a[right] > a[left]) return right;else return left;}else //a[mid] < a[left]{if (a[right] < a[mid]) return mid;else if (a[right] < a[left]) return right;else return left;}}//hoare版本
int Partition1(int* a, int left, int right)
{int midi = GetMidIndax(a, left, right);Swap(&a[left],&a[midi]);int keyi = left;while (left < right){//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}//快排(递归版本)
void QuickSort(int* a, int begin, int end)
{if (begin >= end) return;int keyi = Partition1(a, begin, end);//前序遍历//递归基准值左边的区间QuickSort(a, begin, keyi - 1);//递归基准值右边的区间QuickSort(a, keyi + 1, end);
}int* sortArray(int* nums, int numsSize, int* returnSize){QuickSort(nums, 0, numsSize - 1);*returnSize = numsSize;return nums;
}
我们发现这题一共21个测试用例,只通过了17个,显示超出时间限制,并且nums里出现了很多2,因为有大量重复元素样例不能通过,这样的基准值key一直是处于数组第一个位置,导致性能下降,出现了最坏的情况,时间复杂度为O(N2)
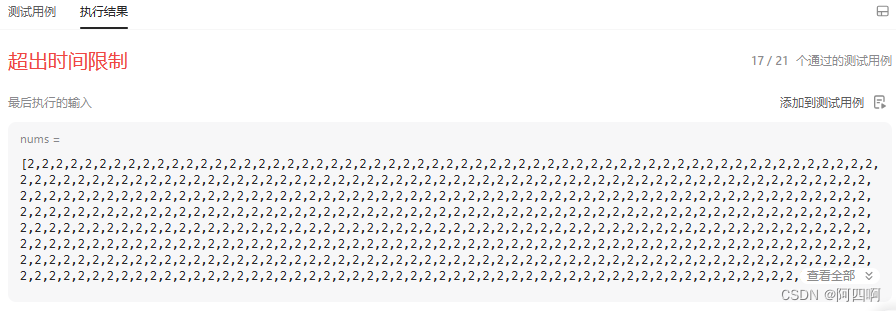
2.解决方案:
- [----------------------------------------------------------------------------------------------------------------------------------------]
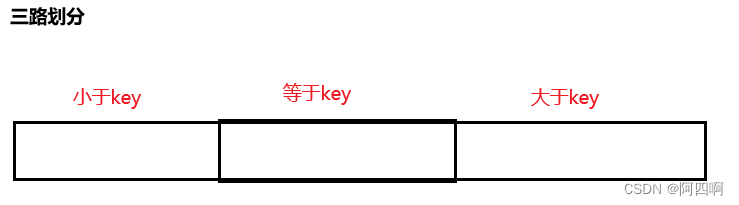
基本思想:三路划分通过将数组划分为三个部分来解决这个问题:小于、等于和大于基准值的元素。
- 用随机值三数取中法选择一个基准值
key。- 定义三个指针变量:
left、cur、right,left的初始值为区间的起始位置,cur指针的初始值为left + 1,right指针的初始值为区间的末尾位置。- 遍历数组,通过与基准值的比较将元素分成三部分:
- 如果当前元素小于
key,将它与left指针所指的位置交换,然后将left指针和cur指针都向右移动。- 如果当前元素等于
key,将cur指针向右移动。- 如果当前元素大于
key,将它与right指针所指的位置交换,然后将right指针向左移动。left指针和right指针之间的区域(包含left和right)即为与key相等的所有元素,然后前序遍历,对left指针左边区域进行递归,right指针右边区域进行递归。- 最终,数组会被划分为三个区域:小于
key区域 、等于key区域 和大于key区域。
3.代码参考
/*** Note: The returned array must be malloced, assume caller calls free().*/
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
int GetMidIndax(int* a,int left, int right)
{int mid = left + (rand() % (right - left));if (a[mid] > a[left]){if (a[right] > a[mid]) return mid;else if (a[right] > a[left]) return right;else return left;}else //a[mid] < a[left]{if (a[right] < a[mid]) return mid;else if (a[right] < a[left]) return right;else return left;}}
//三路分割 左 l r 右
void QuickSort(int* a, int begin, int end)
{if (begin >= end) return;int left = begin;int right = end;int cur = left + 1;int mid = GetMidIndax(a, begin, end);Swap(&a[mid],&a[left]);int key = a[left];while (cur <= right){if (a[cur] < key){Swap(&a[cur], &a[left]);left++;cur++;}else if (a[cur] > key){Swap(&a[cur], &a[right]);right--;}else //a[cur] == key{cur++;}}// [begin left- 1],[left,right],[right + 1,end]QuickSort(a, begin, left - 1);QuickSort(a, right + 1, end);
}int* sortArray(int* nums, int numsSize, int* returnSize){srand(time(NULL));QuickSort(nums, 0, numsSize - 1);*returnSize = numsSize;return nums;
}
相关文章:

【数据结构与算法篇】手撕八大排序算法之快排的非递归实现及递归版本优化(三路划分)
👻内容专栏: 《数据结构与算法篇》 🐨本文概括: 利用数据结构栈(Stack)来模拟递归,实现快排的非递归版本;递归版本测试OJ题时,有大量重复元素样例不能通过,导致性能下降࿰…...
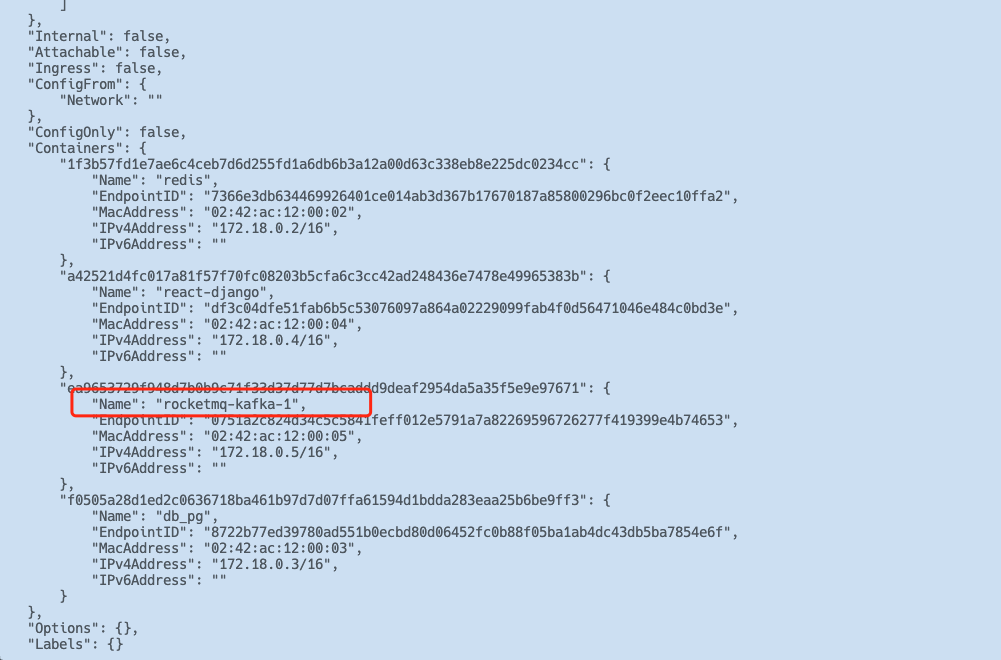
docker network
docker network create <network>docker network connect <network> <container>docker network inspect <network>使用这个地址作为host即可 TODO:添加docker-compose...
回归预测 | MATLAB实现DBN-ELM深度置信网络结合极限学习机多输入单输出回归预测
回归预测 | MATLAB实现DBN-ELM深度置信网络结合极限学习机多输入单输出回归预测 目录 回归预测 | MATLAB实现DBN-ELM深度置信网络结合极限学习机多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现DBN-ELM深度置信网络结合极限学习…...

新亮点!安防视频监控/视频集中存储/云存储平台EasyCVR平台六分屏功能展示
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...

深入解析SNMP协议及其在网络设备管理中的应用
SNMP(Simple Network Management Protocol,简单网络管理协议)作为一种用于网络设备管理的协议,在实现网络设备的监控、配置和故障排除方面发挥着重要的作用。本文将深入解析SNMP协议的工作原理、重要概念和功能,并探讨…...

【SA8295P 源码分析】86 - AIS Camera Device 设备初始化 之 AisProcChainManager 模块初始化源码分析
【SA8295P 源码分析】86 - AIS Camera Device 设备初始化 之 AisProcChainManager 模块初始化源码分析 一、AisProcChainManager::CreateInstance()二、AisPProcIsp::Create()三、AisPProcGpu::Create()系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接…...

十五、pikachu之CSRF
文章目录 一、CSRF概述二、CSRF实战2.1 CSRF(get)2.2 CSRF之token 一、CSRF概述 Cross-site request forgery 简称为“CSRF”,在CSRF的攻击场景中攻击者会伪造一个请求(这个请求一般是一个链接),然后欺骗目标用户进行点击…...
C语言网络编程:实现自己的高性能网络框架
一般生产环境中最耗时的其实是业务逻辑处理。所以,是不是可以将处理业务逻辑的代码给拆出来丢到线程池中去执行。 比如像下面这样: 我们事先创建好一堆worker线程,主线程accepter拿到一个连接上来的套接字,就从线程池中取出一个…...

hive表向es集群同步数据20230830
背景:实际开发中遇到一个需求,就是需要将hive表中的数据同步到es集群中,之前没有做过,查看一些帖子,发现有一种方案挺不错的,记录一下。 我的电脑环境如下 软件名称版本Hadoop3.3.0hive3.1.3jdk1.8Elasti…...

五、Kafka消费者
目录 5.1 Kafka的消费方式5.2 Kafka 消费者工作流程1、总体流程2、消费者组原理3、消费者组初始化流程4、消费者组详细消费流程 5.3 消费者API1 独立消费者案例(订阅主题)2 独立消费者案例(订阅分区)3 消费者组案例 5.4 生产经验—…...

类 中下的一些碎片知识点
判断下面两个函数是否能同时存在 void Print(); void Pirnt() const 答:能同时存在,因为构成函数重载(注意函数的返回值不同是不能构成函数重载的)。 const 对象能调用 非const 成员函数吗 答:不能,因为权…...

JVM第二篇 类加载子系统
JVM主要包含两个模块,类加载子系统和执行引擎,本篇博客将类加载子系统做一下梳理总结。 目录 1. 类加载子系统功能 2. 类加载子系统执行过程 2.1 加载 2.2 链接 2.3 初始化 3. 类加载器分类 3.1 引导类加载器 3.2 自定义加载器 3.2.1 自定义加载器实…...
火爆全网!HubSpot CRM全面集成,引爆营销业绩!
HubSpot CRM是什么?它是一款强大的客户关系管理工具,专为企业优化销售、服务和市场营销流程而设计。它在B2B行业中扮演着极为重要的角色,让我来告诉你为什么吧! HubSpot CRM不仅拥有用户友好的界面和强大的功能,还能够…...
远程调试环境
一、远程调试 1.安装vscode 2.打开vscode,下载插件Remote-SSH,用于远程连接 3.安装php debug 4.远程连接,连接到远端服务器 注:连接远程成功后,在远程依然要进行安装xdebug,刚才只是在vscode中进行的安装。 5.配置la…...
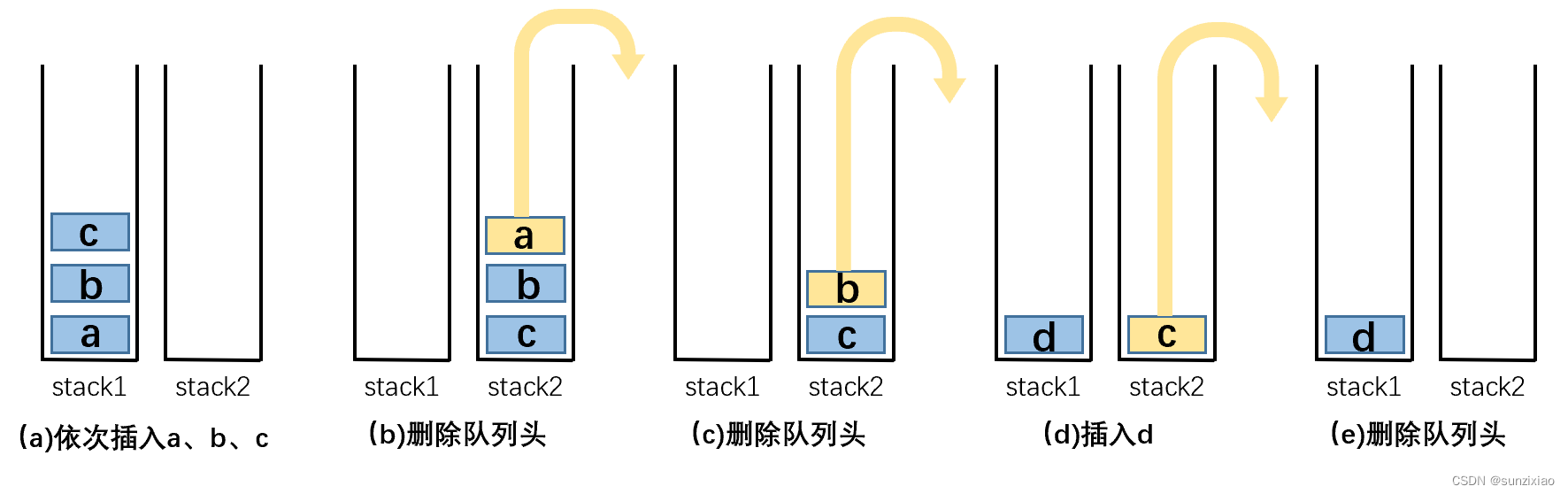
Java面试之用两个栈实现队列
文章目录 题目一、什么是队列和栈?1.1队列1.2栈 二、具体实现2.1 思路分析2.2代码实现 题目 用两个栈实现一个队列,实现在队列尾部插入节点和在队列头部删除节点的功能。 一、什么是队列和栈? 1.1队列 队列是一种特殊的线性表,…...

Python-实用的文件管理及操作
本章,来说说,个人写代码过程中,对于文件管理常用的几种操作。 三个维度 1、指定文件的路径拼接2、检查某文件是否存在3、配置文件的路径管理 1、指定文件的路径拼接 这个操作可以用来管理文件路径也就是上述中的第三点。但是,这里…...
Mysql 事物与存储引擎
MySQL事务 MySQL 事务主要用于处理操作量大,复杂度高的数据。比如说,在人员管理系统中, 要删除一个人员,即需要删除人员的基本资料,又需要删除和该人员相关的信息,如信箱, 文章等等。这样&#…...

java.lang.classnotfoundexception: com.android.tools.lint.client.api.vendor
Unity Android studio打包报错修复 解决方式 java.lang.classnotfoundexception: com.android.tools.lint.client.api.vendor 解决方式 在 launcherTemplate 目录下找到 Android/lintOptions 选项 加上 checkReleaseBuilds false lintOptions { abortOnError false checkRelea…...

pytest fixture夹具,@pytest.fixture
fixture 是pytest 用于测试前后进行预备,清理工作的代码处理机制 fixture相对于setup 和teardown: fixure ,命名更加灵活,局限性比较小 conftest.py 配置里面可以实现数据共享,不需要import 就能自动找到一些配置 setu…...

YOLOv7源码解析
YOLOv7源码解析 YAML文件 YAML文件 以yolov7 cfg/yolov7-w6-pose.yaml为例: # parametersnc: 1 # number of classes nkpt: 4 # number of key points depth_multiple: 1.0 # model depth multiple width_multiple: 1.0 # layer channel multiple dw_conv_kpt:…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
