动态规划(Dynamic programming)讲解(线性 DP 篇)
文章目录
- 动态规划(Dynamic Programing)
- 第一关:线性DP
- 第一战: C F 191 A . D y n a s t y P u z z l e s \color{7F25DF}{CF191A.\space Dynasty\enspace Puzzles} CF191A. DynastyPuzzles
- 题目描述
- 难度: ☆☆☆ \color{blue}{☆☆☆} ☆☆☆
- 题目大意
- 题目描述
- 输入
- 输出
- 思路
- 状态的定义:
- 转移的推导
- 边界的确定
- 结果的输出
- 一首小诗作为总结:
- 时间复杂度: O ( n ) \color{blue}{O(n)} O(n)
- 代码
- 恭喜您,成功战胜了 C F 191 A . D y n a s t y P u z z l e s \color{7F25DF}{CF191A.\space Dynasty\enspace Puzzles} CF191A. DynastyPuzzles,奖励怪兽等级一份:
- 第二战: C F 455 A . B o r e d o m \color{F9E55D}{CF455A. \enspace Boredom} CF455A.Boredom
- 题目描述
- 难度: ☆☆ \color{blue}{☆☆} ☆☆
- 题目大意
- 输入
- 输出
- 思路
- 状态的定义:
- 转移的推导
- 边界的确定
- 结果的输出
- 一首小诗总结一下
- 时间复杂度: O ( n ) \color{blue}{O(n)} O(n)
- 代码
- 恭喜您,成功战胜了 C F 455 A . B o r e d o m \color{F9E55D}{CF455A. \enspace Boredom} CF455A.Boredom,奖励继续看题(嘿嘿)
- 第三战: C F 1061 C . M u l t i p l i c i t y \color{7F25DF}{CF1061C. \enspace Multiplicity} CF1061C.Multiplicity
- 题目描述
- 难度: ☆☆☆ \color{blue}{☆☆☆} ☆☆☆
- 题目大意
- 思路
- 状态的定义:
- 转移的推导
- 边界的确定
- 结果的输出
- 动归的优化
- 一首小诗总结一下
- 时间复杂度: O ( n n ) \color{blue}{O(n\sqrt{n})} O(nn)
- 代码
- 恭喜您,成功战胜了 C F 1061 C . M u l t i p l i c i t y \color{7F25DF}{CF1061C. \enspace Multiplicity} CF1061C.Multiplicity,奖励一次问而必答的机会,验证码
6AZ70(~~好像没什么用~~ )+简单题讲解。 - 第四战: A B C 311 E − D e f e c t f r e e S q u a r e s \color{F9E55D}{ABC311E - Defect\ free\ Squares} ABC311E−Defect free Squares
- 题目描述
- 题目大意
- 思路
- 状态的定义
- 转移的推导(难点)
- 边界的确定
- 结果的输出
- 一首小诗总结一下
- 代码
- 时间复杂度: O ( n m ) O(nm) O(nm)
- 恭喜你,成功战胜了 A B C 311 E − D e f e c t f r e e S q u a r e s \color{F9E55D}{ABC311E - Defect\ free\ Squares} ABC311E−Defect free Squares,奖励继续看题~~~
- 第五战: C S E S − 1638 G r i d P a t h s \color{97EF6A}{CSES-1638\ Grid\ Paths} CSES−1638 Grid Paths
- 题目描述
- 题目大意
- 思路
- 状态的定义:
- 转移的推导
- 边界的确定
- 结果的输出
- 一首小诗总结一下
- 代码
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 恭喜您,成功战胜了 C S E S − 1638 G r i d P a t h s \color{97EF6A}{CSES-1638\ Grid\ Paths} CSES−1638 Grid Paths,奖励无:
动态规划(Dynamic Programing)
动态规划就是通过记住过去所算过的值,来防止重复计算所带来的弊端。这就是为什么动态规划也可以写成记忆化搜索的形式。
下面,我们通过 DP 的题目,假设我们对其的感悟!(大家可以边看边做一下这几道题,都是很好的题目)
第一关:线性DP
第一战: C F 191 A . D y n a s t y P u z z l e s \color{7F25DF}{CF191A.\space Dynasty\enspace Puzzles} CF191A. DynastyPuzzles
题目描述
难度: ☆☆☆ \color{blue}{☆☆☆} ☆☆☆
题目大意
题目描述
有一个王朝,他们国王的名字用姓氏的简写来标记每一代。为了保证王朝的稳定,现在这个王朝的继承人的名字需要满足继承者名字的第一个字母要和前代名字最后一个字母相同。然后拼接起来的名字,第一个字母和最后一个字母相同。现在有一个考古博士,知道了这个王朝国王和亲戚的名字。问你这个王朝所能够得到的最长字符串。
输入
第一行一个整数 n n n ( 1 ≤ n ≤ 5 ⋅ 1 0 5 1≤n≤5·10^5 1≤n≤5⋅105),接下来 n n n行,每行一个非空字符串,全由小写字母组成,字符串长度不超过 10 10 10。
输出
最长满足要求的长度,如果没有输出 0 0 0。
思路
动态规划莫过于 4 4 4 步:
- 状态的定义
- 转移的推导
- 边界的确定
- 结果的输出
状态的定义:
可以设 f i , j f_{i, j} fi,j 表示当前名字的第一个字母为 i i i,最后一个字母为 j j j 的最长串。
但是,字母不容易开数组,所以我们可以将其压缩成 0 ∼ 26 0\sim26 0∼26 的整数。
转移的推导
之后,我们不难想到对于每一个长度为 n n n 字符串 S S S, f j , S n = m a x ( f j , S n , f j , S 1 + n ) f_{j, S_n}=max(f_{j, S_n}, f_{j, S_1} + n) fj,Sn=max(fj,Sn,fj,S1+n)。
注意,如果这是我们所拼接的第一个串,那么 f S 1 , S n = n f_{S_1, S_n} = n fS1,Sn=n,不能在通过上面的转移方式转移,因为第一个字母只能是 S 1 S_1 S1
边界的确定
因为,我们要确定每一个串是否是我们拼接的第一个串,所以我们上来要把 f f f 数组全部赋值为 i n t int int 的最小值。
结果的输出
那么这道题最终他的名字其实就是首位字母相同的串,故所有串中首位相同的最长串即为答案!
r e s = m a x ( f i , i ) res=max(f_{i, i}) res=max(fi,i)
一首小诗作为总结:
名字首 i i i 最后 j j j,状态设为 f i , j f_{i, j} fi,j
方程转移枚举头,加入 i i i 串转移透。
边界一定要注意,设小为保第一串。
最后结果首尾同,即为最值 f i , i f_{i,i} fi,i
时间复杂度: O ( n ) \color{blue}{O(n)} O(n)
代码
#include <bits/stdc++.h>
#define int long longusing namespace std;const int N = 30;int n;
string name;
int f[N][N];signed main()
{cin >> n;memset(f, -0x3f, sizeof f);for (int i = 1; i <= n; i ++){cin >> name;int len = name.size(), l = name[0] - 'a', r = name.back() - 'a';for (int j = 0; j < 26; j ++)f[j][r] = max(f[j][r], f[j][l] + len);f[l][r] = max(f[l][r], len); //初始所有值都是-0x3f3f3f3f,所以取个max就能够让第一个串赋值}int res = 0;for (int k = 0; k < 26; k ++)res = max(res, f[k][k]);cout << res << endl;return 0;
}
恭喜您,成功战胜了 C F 191 A . D y n a s t y P u z z l e s \color{7F25DF}{CF191A.\space Dynasty\enspace Puzzles} CF191A. DynastyPuzzles,奖励怪兽等级一份:
B r o n z e M o n s t e r \color{97EF6A}{Bronze\enspace Monster} BronzeMonster
U n u s u a l M o n s t e r \color{F9E55D}{Unusual\enspace Monster} UnusualMonster
E p i c M o n s t e r \color{7F25DF}{Epic\enspace Monster} EpicMonster
L e g e n d a r y M o n s t e r \color{CC1D26}{Legendary\enspace Monster} LegendaryMonster
第二战: C F 455 A . B o r e d o m \color{F9E55D}{CF455A. \enspace Boredom} CF455A.Boredom
题目描述
难度: ☆☆ \color{blue}{☆☆} ☆☆
题目大意
给定一个有 n n n 个元素的序列 { a n } \{a_n\} {an}。你可以做若干次操作。在一次操作中我们可以取出一个数(假设他为 x x x)并删除它,同时删除所有的序列中值为 x + 1 x+1 x+1 和 x − 1 x-1 x−1 的数。这一步操作会给玩家加上 x x x 分。
输入
输入格式 第一行一个整数 n ( 1 ≤ n ≤ 1 0 5 ) n(1\le n\le 10^5) n(1≤n≤105),说明这个序列有多少数。 第二行 n n n 个整数,分别表示 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an。
输出
一个整数,表示玩家最多能获得多少分
思路
动态规划 4 4 4 步:
- 状态的定义
- 转移的推导
- 边界的确定
- 结果的输出
状态的定义:
首先我们会想到设 f i , 0 / 1 f_{i, 0/1} fi,0/1 表示 a i a_i ai删除或者是不删除,但是发现不是很好转移,于是我们可以
嘿嘿,才怪。故而,我们再想一想,他前后删除的是所有值,所以设 f i , 0 / 1 f_{i, 0/1} fi,0/1 表示前 i i i 个数中,数字 i i i 删除还是不删除会不会简单一些呢?

转移的推导
不难想到,设 c n t i cnt_i cnti 为 i i i 出现的次数,
{ f i , 1 = m a x ( f i − 2 , 0 , f i − 2 , 1 ) + c n t i × i f i , 0 = m a x ( f i − 1 , 1 , f i − 1 , 0 ) \begin{cases} & f_{i, 1} = max(f_{i - 2, 0}, f_{i - 2, 1})+cnt_i\times i\\ & f_{i, 0} = max(f_{i - 1, 1}, f_{i - 1, 0}) \end{cases} {fi,1=max(fi−2,0,fi−2,1)+cnti×ifi,0=max(fi−1,1,fi−1,0)
因为,如果选了数 i i i,那么贡献就是 c n t i × i cnt_i\times i cnti×i,那么 i − 1 i - 1 i−1 也一定不能选。但是 i − 2 i - 2 i−2 是可以选的呀!如果不选数 i i i,那么就考虑 i − 1 i - 1 i−1选不选。
边界的确定

结果的输出
不难想,就是 m a x ( f m x , 0 , f m x , 1 ) max(f_{mx, 0}, f_{mx, 1}) max(fmx,0,fmx,1), m x mx mx表示序列中最大的元素。
因为,我们考虑了前面所有的元素,最终就是这两个取其一!
一首小诗总结一下
这题状态要小心,不设下标却设数。
转移若选找前 2 2 2,如果不选看前值。
边界确定仔细想,貌似根本不需要。
最终结果找 m x mx mx,选或不选取个 m a x max max。
时间复杂度: O ( n ) \color{blue}{O(n)} O(n)
代码
#include <bits/stdc++.h>
#define int long longusing namespace std;const int N = 1e5 + 10;int n;
int a[N], f[N][2], cnt[N];signed main()
{cin >> n;int mx = 0;for (int i = 1; i <= n; i ++)cin >> a[i], cnt[a[i]] ++, mx = max(mx, a[i]);for (int i = 1; i <= mx; i ++){f[i][1] = max(f[i - 2][1], f[i - 2][0]) + cnt[i] * i;f[i][0] = max(f[i - 1][1], f[i - 1][0]);}cout << max(f[mx][1], f[mx][0]) << endl;return 0;
}
恭喜您,成功战胜了 C F 455 A . B o r e d o m \color{F9E55D}{CF455A. \enspace Boredom} CF455A.Boredom,奖励继续看题(嘿嘿)
第三战: C F 1061 C . M u l t i p l i c i t y \color{7F25DF}{CF1061C. \enspace Multiplicity} CF1061C.Multiplicity
题目描述
难度: ☆☆☆ \color{blue}{☆☆☆} ☆☆☆
题目大意
从序列 { a 1 , a 2 , . . , a n } \{a_1,\ a_2,\ ..\ ,\ a_n\} {a1, a2, .. , an} 中选出非空子序列 { b 1 , b 2 , . . , b k } \{b_1,\ b_2,\ ..\ ,\ b_k\} {b1, b2, .. , bk},一个子序列合法需要满足 ∀ i ∈ [ 1 , k ] , i ∣ b i \forall\ i \in [1,\ k],\ i\ |\ b_i ∀ i∈[1, k], i ∣ bi。求有多少互不相等的合法子序列,答案对 1 0 9 + 7 10^9 + 7 109+7 取模。
序列 { 1 , 1 } \{1,\ 1\} {1, 1} 有 2 2 2 种选法得到子序列 { 1 } \{1\} {1},但 1 1 1 的来源不同,认为这两个子序列不相等。
思路
动态规划需要 5 5 5 步了:
- 状态的定义
- 转移的推导
- 边界的确定
- 结果的输出
- 动归的优化
状态的定义:
由于题意中设计到了第 i i i 个数必须被 i i i整除,所以我们可以想到长度,于是可以考虑用 f i , j f_{i, j} fi,j 表示对于前 i i i 个数来说,长度为 j j j 的方案数。
转移的推导
{ f i , j = f i , j + f i − 1 , j j ∣ a i f i , j = f i − 1 , j o t h e r w i s e \begin{cases} & f_{i, j} = f_{i, j} + f_{i - 1, j} &j\mid a_i\\ & f_{i, j} = f_{i-1,j} &otherwise \end{cases} {fi,j=fi,j+fi−1,jfi,j=fi−1,jj∣aiotherwise
因为,如果 a i a_i ai 是 j j j 的倍数,那么就可以加入序列中,所以可以加上前一个长度。反之,不可以,不能加入,所以长度不减 1 1 1。
边界的确定
起初,长度为 0 0 0 时规定有一种转移方式,即 f 0 , 0 = 1 f_{0, 0}=1 f0,0=1。
结果的输出
最终的结果就是所有可能长度之和,即 r e s = ∑ i = 1 n f n , i res=\sum\limits_{i=1}^{n}f_{n, i} res=i=1∑nfn,i
动归的优化
这道题涉及到了动态规划的优化,因为我们会发现,两维的状态根本开不出来,会炸!
所以,这时候,细心地我们发现转移的时候只用到了 i − 1 i-1 i−1,那么我们就可以仿照01背包的方式,用个滚动数组把第一维滚掉,当然这样在枚举长度的时候要倒着枚举!
OK,数组是开下了,可是时间呢?还是炸,我们不妨算一下,#^&%!$# ……*&%¥&@,时间复杂度 O ( n 2 ) O(n^2) O(n2)!完了,芭比球了!
没事,不要慌,慌你就输了。我们再细心的观察一下,就会发现,咦好像只有在 j ∣ a i j\mid a_i j∣ai的时候才可以转移,所以我们就能够先把 a i a_i ai 的约数列出来( O ( n ) O(\sqrt{n}) O(n)),然后进行转移( O ( n ) O\sqrt(n) O(n))。
诶?好像可以了诶,时间复杂度到了 O ( n n ) O(n\sqrt{n}) O(nn),这样就可以跑过去了!
一首小诗总结一下
状态无妨设两维,之后再用滚动压。
转移只当 j ∣ a j\mid a j∣a,所以可以找约数。
边界 0 0 0 长设为 1 1 1,之后才可好转移。
最后求和所有长,直接输出 A C AC AC 现。
时间复杂度: O ( n n ) \color{blue}{O(n\sqrt{n})} O(nn)
代码
#include <bits/stdc++.h>
#define int long longusing namespace std;const int N = 1e6 + 10, mod = 1e9 + 7;int n;
int a[N];
int f[N];
vector<int> gt;signed main()
{cin >> n;f[0] = 1;for (int i = 1; i <= n; i ++){cin >> a[i];gt.clear();for (int j = 1; j <= a[i] / j; j ++)if (a[i] % j == 0){gt.push_back(j);if (a[i] / j != j) gt.push_back(a[i] / j);}sort(gt.begin(), gt.end(), greater<int>());for (auto c : gt)f[c] = (f[c] + f[c - 1]) % mod;}int res = 0;for (int i = 1; i <= n; i ++)res = (res + f[i]) % mod;cout << res << endl;return 0;
}
恭喜您,成功战胜了 C F 1061 C . M u l t i p l i c i t y \color{7F25DF}{CF1061C. \enspace Multiplicity} CF1061C.Multiplicity,奖励一次问而必答的机会,验证码6AZ70(好像没什么用 )+简单题讲解。
第四战: A B C 311 E − D e f e c t f r e e S q u a r e s \color{F9E55D}{ABC311E - Defect\ free\ Squares} ABC311E−Defect free Squares
题目描述
题目大意
给出一个 H × W H\times W H×W 的矩阵,每个位置要么有洞,要么没洞,问有多少个每个元素均为正整数的三元组 ( x , y , n ) (x,y,n) (x,y,n),满足:
x + n − 1 ≤ H x+n-1\le H x+n−1≤H, y + n − 1 ≤ W y+n-1\le W y+n−1≤W,以 ( x , y ) (x,y) (x,y) 为左上角、 ( x + n − 1 , y + n − 1 ) (x+n-1,y+n-1) (x+n−1,y+n−1) 为右下角的矩阵每个位置都没有洞。
H , W ≤ 3000 H,W\le 3000 H,W≤3000,洞的个数不超过 1 0 5 10^5 105。
思路
动态规划 4 4 4 步:
- 状态的定义
- 转移的推导
- 边界的确定
- 结果的输出
状态的定义
我们不难想到设 f i , j f_{i, j} fi,j 表示以 ( i , j ) (i, j) (i,j) 正方形右下角的方案数。(这并不是本题的难点)
转移的推导(难点)
对于每一个 f i , j f_{i, j} fi,j,我们考虑他的推导:
- 如果 A i , j A_{i, j} Ai,j 为洞,那么不会有合法的正方形,故 f i , j = 0 f_{i, j}=0 fi,j=0
- 如果 A i , j A_{i, j} Ai,j 不为洞,那么考虑从三个方向转移:
- 那么 f i , j = min ( f i − 1 , j , f i , j − 1 , f i − 1 , j − 1 ) + 1 f_{i, j} = \min(f_{i - 1, j}, f_{i, j - 1}, f_{i - 1, j - 1}) + 1 fi,j=min(fi−1,j,fi,j−1,fi−1,j−1)+1,首先,这里的 + 1 +1 +1 就是会多出 i , j i, j i,j 自己作为一个正方形,对于取 min \min min 的段落,就是通过 3 3 3 个点来确定出从 ( i , j ) (i, j) (i,j) 这个点可以向外延伸多长,下面有几个误区澄清一下:
- 误区1:有些人会考虑取最大值
- 这是不对的,考虑设 x 1 x_1 x1 为以 i − 1 , j i - 1, j i−1,j 为右下角的合法正方形的最大边长, x 2 x_2 x2 为以 i − 1 , j − 1 i - 1, j - 1 i−1,j−1 为右下角的合法正方形的最大边长, x 3 x_3 x3 为以 i − 1 , j − 1 i - 1, j - 1 i−1,j−1 为右下角的合法正方形的最大边长。其实 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 就是我们的 f i − 1 , j , f i , j − 1 , f i − 1 , j − 1 f_{i - 1, j}, f_{i, j - 1}, f_{i - 1, j - 1} fi−1,j,fi,j−1,fi−1,j−1,因为如果边长为 x 1 x_1 x1的正方形是合法的,那么比 x 1 x_1 x1 边长小的正方形也一定合法,又因为我们取得是最大边长,所以就等同于 f i − 1 , j , f i , j − 1 , f i − 1 , j − 1 f_{i - 1, j}, f_{i, j - 1}, f_{i - 1, j - 1} fi−1,j,fi,j−1,fi−1,j−1。之后,我们考虑假设 x 1 x_1 x1 最大,那难道答案就是 x 1 x_1 x1吗?当然不是,因为 ( i − x 3 , j − x 3 ) (i - x_3, j -x_3) (i−x3,j−x3)这个点一定是有洞的,那么如果按我们的理解从 ( i − x 1 , j − x 1 + 1 ) (i-x_1, j-x_1 + 1) (i−x1,j−x1+1) 到 ( i , j ) (i,j) (i,j)都是无洞的。但是 i − x 1 < i − x 3 i-x_1 < i-x_3 i−x1<i−x3 且 j − x 1 + 1 ≤ j − x 3 j-x_1 + 1\le j-x_3 j−x1+1≤j−x3,所以一定包含点 ( i − x 3 , j − x 3 ) (i - x_3, j -x_3) (i−x3,j−x3),即答案不是 x 1 x_1 x1。以此类推,我们就可以证明出答案其实是最小值
- 误区2:有些人会认为可以不加 ( i − 1 , j − 1 ) (i-1,j-1) (i−1,j−1)
- 这个很好反驳,给个例子就行了
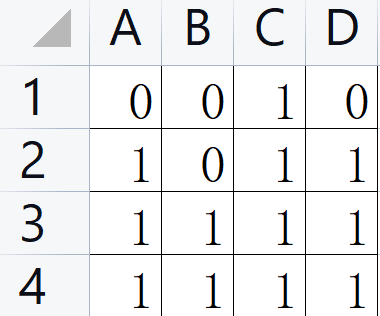
假设,我们当前枚举到了 D 4 D4 D4,那么如果光通过 D 3 D3 D3 和 C 4 C4 C4 转移,方案数为 2 2 2,不过真的对吗?其实是错的因为 B 2 B2 B2 这个点并没有在状态之内,就会发生状态的遗漏。所以,必须加入 ( i − 1 , j − 1 ) (i-1,j-1) (i−1,j−1),这样才能保证,正方形区域内全是 1 1 1。
- 这个很好反驳,给个例子就行了
边界的确定

结果的输出
最终答案不难想,就是以每个 ( i , j ) (i, j) (i,j) 为正方形右下角的方案数之和,即 r e s = ∑ i = 1 n ∑ j = 1 m f i , j res=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}f_{i,j} res=i=1∑nj=1∑mfi,j
一首小诗总结一下
代码
#include <iostream>
#define int long longusing namespace std;const int N = 3e3 + 10;int n, m, k;
int a, b;
int mp[N][N], dp[N][N];signed main()
{cin >> n >> m >> k;for (int i = 1; i <= k; i ++)cin >> a >> b, mp[a][b] = 1;int res =0 ;for (int i = 1; i <= n; i ++)for (int j = 1; j <= m; j ++){dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;if (mp[i][j])dp[i][j] = 0;res += dp[i][j];}cout << res << endl;return 0;
}
时间复杂度: O ( n m ) O(nm) O(nm)
恭喜你,成功战胜了 A B C 311 E − D e f e c t f r e e S q u a r e s \color{F9E55D}{ABC311E - Defect\ free\ Squares} ABC311E−Defect free Squares,奖励继续看题~~~
第五战: C S E S − 1638 G r i d P a t h s \color{97EF6A}{CSES-1638\ Grid\ Paths} CSES−1638 Grid Paths
题目描述
题目大意
给出一个 n × n n\times n n×n 的网格,其中 * 表示当前点不可走,.表示当前点可走,每次只能向右或向左走,问从 ( 1 , 1 ) (1, 1) (1,1) 走到 ( n , n ) (n,n) (n,n) 的方案数,对 1 0 9 + 7 10^9+7 109+7 取模。
思路
动态规划莫过于 4 4 4 步:
- 状态的定义
- 转移的推导
- 边界的确定
- 结果的输出
状态的定义:
可以设 f i , j f_{i, j} fi,j 表示从 ( 1 , 1 ) (1,1) (1,1) 走到 ( i , j ) (i,j) (i,j) 的方案数。
转移的推导
比较简单,直接写吧:
f i , j = { f i , j + f i − 1 , j G i − 1 , j ≠ ∗ f i , j + f i , j − 1 G i , j − 1 ≠ ∗ f_{i,j}=\begin{cases} & f_{i,j}+f_{i-1,j} & G_{i-1,j}\ne*\\ & f_{i,j} + f_{i,j-1} & G_{i,j-1}\ne* \end{cases} fi,j={fi,j+fi−1,jfi,j+fi,j−1Gi−1,j=∗Gi,j−1=∗
边界的确定
f 1 , 1 = 1 f_{1,1}=1 f1,1=1
结果的输出
r e s = f n , n res=f_{n,n} res=fn,n
一首小诗总结一下
起点至坐标 ( i , j ) (i, j) (i,j),方案设为 f i , j f_{i, j} fi,j
转移先判能否转,之后再加方案数。
边界此时要确定,起点自身 1 1 1 方案。
输出终点方案数,天空巨响 A C AC AC 现
代码
#include <bits/stdc++.h>
#define int long longusing namespace std;const int N = 1e3 + 10, mod = 1e9 + 7;int n;
char g[N][N];
int f[N][N];signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> n;for (int i = 1; i <= n; i ++)for (int j = 1; j <= n; j ++)cin >> g[i][j];if (g[1][1] != '*') f[1][1] = 1; //注意:如果第一个点是*就不能在往后推导了for (int i = 1; i <= n; i ++)for (int j = 1; j <= n; j ++){if (g[i][j] == '*') continue;int Way1 = f[i - 1][j], Way2 = f[i][j - 1];if (g[i - 1][j] == '*') Way1 = 0;if (g[i][j - 1] == '*') Way2 = 0;f[i][j] = (f[i][j] + Way1 + Way2) % mod;}cout << f[n][n] << endl;return 0;
}
时间复杂度: O ( n 2 ) O(n^2) O(n2)
恭喜您,成功战胜了 C S E S − 1638 G r i d P a t h s \color{97EF6A}{CSES-1638\ Grid\ Paths} CSES−1638 Grid Paths,奖励无:
相关文章:

动态规划(Dynamic programming)讲解(线性 DP 篇)
文章目录 动态规划(Dynamic Programing)第一关:线性DP第一战: C F 191 A . D y n a s t y P u z z l e s \color{7F25DF}{CF191A.\space Dynasty\enspace Puzzles} CF191A. DynastyPuzzles题目描述难度: ☆☆☆ \color…...

提升开发能力的低代码思路
一、低代码理念 在现代软件开发中,低代码开发平台备受关注。那么,什么是低代码开发平台呢?简单来说,它是一种能够提供丰富的图形化用户界面,让开发者通过拖拽组件和模型就能构建应用的开发环境。与传统开发方式相比&am…...
YAML详解及使用方法
YAML详解及使用方法 一、基本介绍二、数据类型2.1 纯量(scalars)/标量2.1.1 字符串2.1.2 保留换行(Newlines preserved)2.1.3 布尔值(Boolean)2.1.4 整数(Integer)2.1.5 浮点数(Floating Point)2.1.6 空(Nu…...
垃圾回收器
垃圾回收器就是垃圾回收的实践者,随着JDK的发展,垃圾回收器也在不断的更迭,在不同的场合下使用不同的垃圾回收器,这也是JVM调优的一部分。 1.垃圾回收器的分类 按线程可分为单线程(串行)垃圾回收器和多线程(并行)垃圾回收器。 按…...

SpringBoot 读取配置文件的值为 Infinity
1.配置信息 appid:6E212341234 2.获取方式 Value("${admin}")private String admin; 获取到结果 Infinity 3.修改方案 配置信息上加号 appid:‘6E212341234 yml中使用[单引号]不会转换单引号里面的特殊字符,使用""[双…...
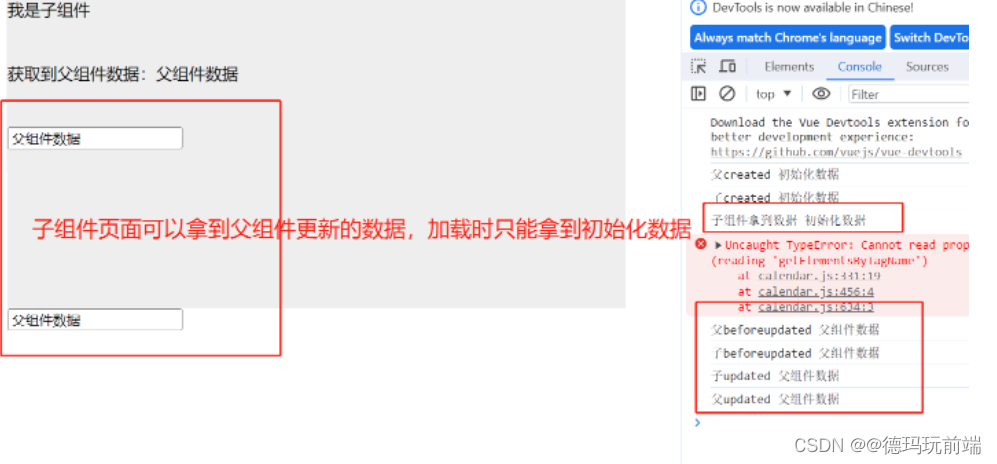
学习笔记230827--vue项目中,子组件拿不到父组件异步获取数据的问题
🧋 问题描述 父组件的数据是请求后台所得,因为是异步数据,就会出现,父组件的值传递过去了,子组件加载不到,拿不到值的问题。 下面从同步数据传递和异步数据传递开始论述问题 🧋🧋1…...

sql:SQL优化知识点记录(三)
(1)explain之select_type和table介绍 简单的查询类型是:simple 外层 primary,括号里subquery 用到了临时表:derived (2)explain之type介绍 trpe反映的结果与我们sql是否优化过,是否…...

List<Map>操作汇总
分组 List<Map> mapList new ArrayList<>(); Map<String,List<Map>> mapListGroup mapList.stream().collect(Collectors.groupingBy(e->e.get("xxx").toString())); 最大值最小值 int max maps.stream().mapToInt(e -> new Inte…...
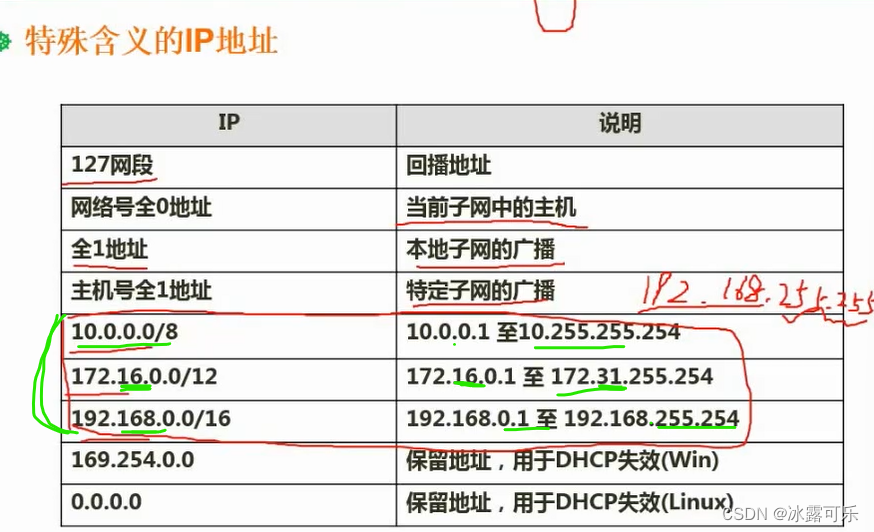
软考:中级软件设计师:网络类型与拓扑结构,网络规划与设计,ip地址与子网划分,特殊含义的IP地址
软考:中级软件设计师:网络类型与拓扑结构 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准…...
linux创建进程
linux创建进程 准备工作 准备工作 在Ubuntu64系统上 1、安装GCC和Make工具 编译器GCC:把C源码转为二进制程序 Make:自动编译多源文件项目 sudo apt-get update #更新存储库 sudo apt-get install build-essential #安装build-essential包 gcc --versio…...

100天精通Golang(基础入门篇)——第19天:深入剖析Go语言中方法(Method)的妙用与实践
🌷🍁 博主猫头虎 带您 Go to Golang Language.✨✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~…...

【人工智能】—_不确定性、先验概率_后验概率、概率密度、贝叶斯法则、朴素贝叶斯_、最大似然估计
【人工智能】— 不确定性、先验概率/后验概率、概率密度、贝叶斯法则、朴素贝叶斯 文章目录 【人工智能】— 不确定性、先验概率/后验概率、概率密度、贝叶斯法则、朴素贝叶斯不确定性不确定性与理性决策基本概率符号先验概率(无条件概率)/后验概率(条件概率)随机变量概率密度联…...

postgresql-字符函数
postgresql-字符函数 字符串连接字符与编码字符串长度大小写转换子串查找与替换截断与填充字符串格式化MD5 值字符串拆分字符串反转 字符串连接 concat(str, …)函数用于连接字符串,并且忽略其中的 NULL 参数;concat_ws(sep, str, …) 函数使用指定分隔…...
网络通信)
VUE笔记(五)网络通信
一、axios的简介 1、什么是axios 文档:Axios 中文文档 | Axios 中文网 | Axios 是一个基于 promise 的网络请求库,可以用于浏览器和 node.js 概念:axios是一个基于Promise的网络请求库,可以用于浏览器和node.js 特点ÿ…...

微信小程序修改数据,input不能实时回显
场景: 填写发票抬头,填写抬头公司时候,会根据用户输入的内容实时获取相关的公司信息,用户选择搜索出来的公司,这时候 setData,但是数据并没有回显,而是需要再需要点一下屏幕。 解决方案: 原来…...
GitHub Copilot三连更:能在代码行里直接提问,上下文范围扩展到终端
量子位 | 公众号 QbitAI 就在昨晚,GitHub Copilot迎来了一波不小的更新。 包括: 全新交互体验——代码行中直接召唤聊天功能,不用切界面,主打一个专注; 改善斜杠命令,一键删除,主打快捷操作、…...
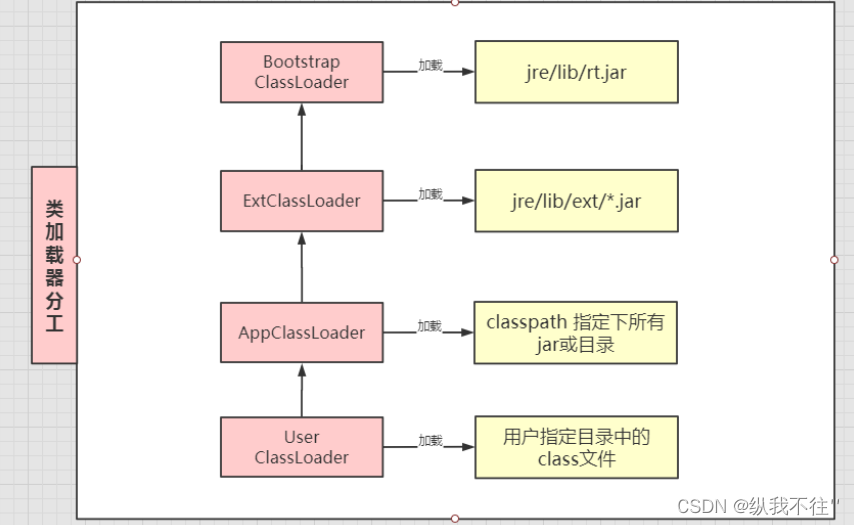
双亲委派机制
双亲委派机制流程 当Application ClassLoader 收到一个类加载请求时,他首先不会自己去尝试加载这个类,而是将这个请求委派给父类加载器Extension ClassLoader去完成。 当Extension ClassLoader收到一个类加载请求时,他首先也不会自己去尝试…...

美团北极星榜单,服务零售的医美新样本
事实证明,任何时候,人们对美的追求都是刚需,只是有时候被压抑了。 德勤中国的《中国医美行业2023年度洞悉报告》(以下简称“报告”)显示,中国医美市场规模预计在2023年超过2000亿元,实现20%增速…...
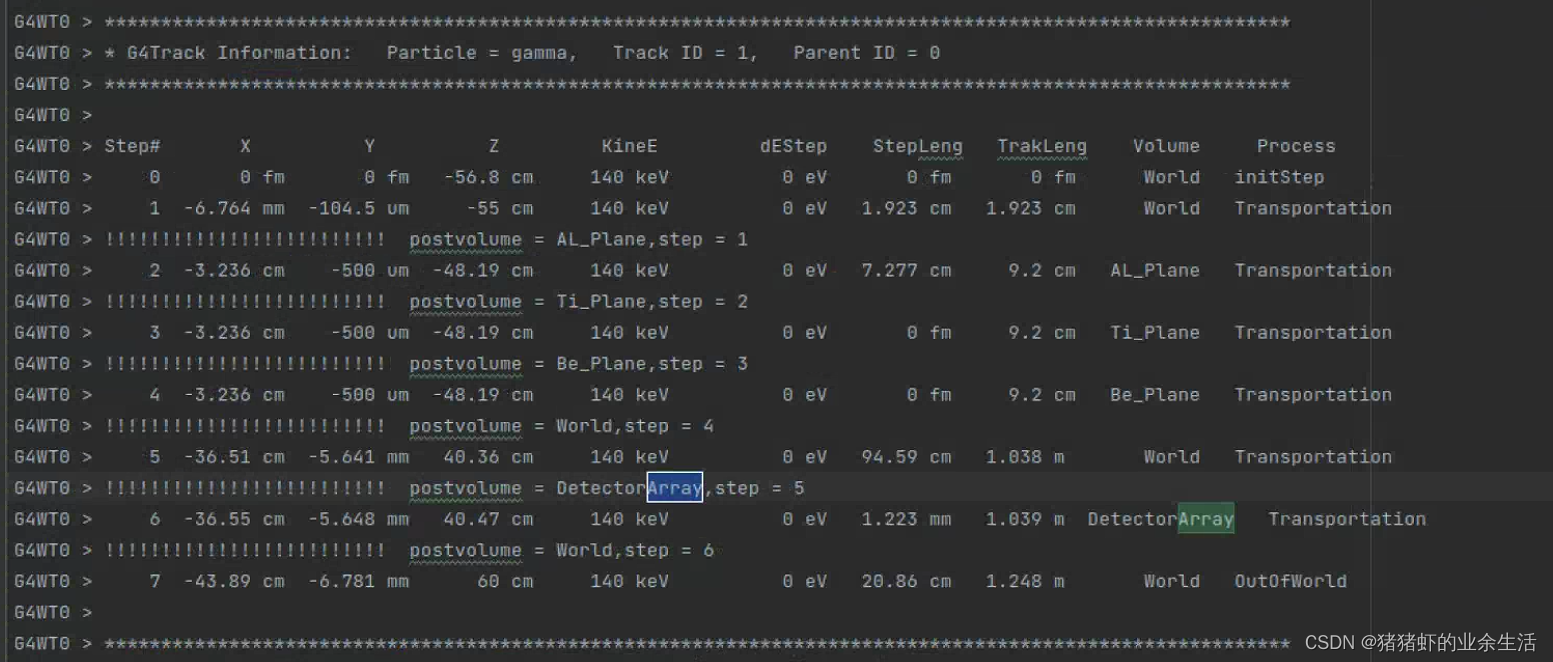
geant4 常用代码
1 获取特特定能量范围的特定粒子 E:\examples_understanding\geant4-v11.0.0_note\examples\extended\runAndEvent\RE02 //-- Particle with kinetic energy filter.G4SDParticleWithEnergyFilter* pkinEFilter new G4SDParticleWithEnergyFilter(fltName"gammaE filter&…...

重要通知!eBay将升级买家满意度考核,如何让你的店铺脱颖而出?
8月份,eBay发布了重要通知,为促进跨境卖家积极提升买家体验,升级了针对卖家的买家满意度考核。其中,产品质量是买家满意度考核的核心,是中国卖家急需提升的重中之重,也是eBay考核的重点。 eBay将着眼于产品…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
