2021年12月 C/C++(五级)真题解析#中国电子学会#全国青少年软件编程等级考试

第1题:书架
John最近买了一个书架用来存放奶牛养殖书籍,但书架很快被存满了,只剩最顶层有空余。
John共有N头奶牛(1 ≤ N ≤ 20,000),每头奶牛有自己的高度Hi(1 ≤ Hi ≤ 10,000),N头奶牛的总高度为S。书架高度为B(1 ≤ B ≤ S < 2,000,000,007).
为了到达书架顶层,奶牛可以踩着其他奶牛的背,像叠罗汉一样,直到他们的总高度不低于书架高度。当然若奶牛越多则危险性越大。为了帮助John到达书架顶层,找出使用奶牛数目最少的解决方案吧。
时间限制:10000
内存限制:65536
输入
第1行:空格隔开的整数N和B 第2~N+1行:第i+1行为整数Hi
输出
能达到书架高度所使用奶牛的最少数目
样例输入
6 40
6
18
11
13
19
11
样例输出
3
以下是使用贪心算法来解决书架问题的C语言代码:
#include <stdio.h>
#include <stdlib.h>#define MAX_N 20000int compare(const void* a, const void* b) {return *(int*)a - *(int*)b;
}int minCows(int heights[MAX_N], int n, int b) {qsort(heights, n, sizeof(int), compare); // 将奶牛的高度排序int sum = 0;int count = 0;for (int i = n - 1; i >= 0; i--) {sum += heights[i];count++;if (sum >= b) {break;}}return count;
}int main() {int n, b;int heights[MAX_N];// 读取输入scanf("%d %d", &n, &b);for (int i = 0; i < n; i++) {scanf("%d", &heights[i]);}// 使用贪心算法求解最少使用的奶牛数目int minCowsCount = minCows(heights, n, b);// 输出结果printf("%d\n", minCowsCount);return 0;
}
该算法使用贪心算法的思想,通过将奶牛的高度进行排序,并从最高的奶牛开始,逐个累加奶牛的高度,直到总高度不低于书架高度B为止。首先,使用快速排序算法对奶牛的高度进行排序。然后,从最高的奶牛开始累加其高度,并记录使用的奶牛数目。如果累加的总高度不低于书架高度B,则停止累加。最后,返回使用的奶牛数目作为答案。
第2题:棋盘问题
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。
时间限制:1000
内存限制:65536
输入
输入含有多组测试数据。 每组数据的第一行是两个正整数,n k,用一个空格隔开,表示了将在一个n*n的矩阵内描述棋盘,以及摆放棋子的数目。 n <= 8 , k <= n 当为-1 -1时表示输入结束。 随后的n行描述了棋盘的形状:每行有n个字符,其中 # 表示棋盘区域, . 表示空白区域(数据保证不出现多余的空白行或者空白列)。
输出
对于每一组数据,给出一行输出,输出摆放的方案数目C (数据保证C<2^31)。
样例输入
2 1
#.
.#
4 4
…#
…#.
.#…
#…
-1 -1
样例输出
2
1
以下是使用回溯法来解决棋盘问题的C语言代码:
#include <stdio.h>
#include <stdbool.h>#define MAX_N 8int count = 0; // 记录可行的摆放方案数bool isValid(char board[MAX_N][MAX_N], int row, int col, int n) {// 检查同一行是否已经有棋子for (int c = 0; c < col; c++) {if (board[row][c] == 'Q') {return false;}}// 检查左上方对角线是否已经有棋子for (int r = row, c = col; r >= 0 && c >= 0; r--, c--) {if (board[r][c] == 'Q') {return false;}}// 检查左下方对角线是否已经有棋子for (int r = row, c = col; r < n && c >= 0; r++, c--) {if (board[r][c] == 'Q') {return false;}}return true;
}void backtrack(char board[MAX_N][MAX_N], int col, int n, int k) {if (col == n) {if (k == 0) {count++;}return;}for (int row = 0; row < n; row++) {if (board[row][col] == '#' && isValid(board, row, col, n)) {board[row][col] = 'Q';backtrack(board, col + 1, n, k - 1);board[row][col] = '#';}}backtrack(board, col + 1, n, k);
}int chessboard(int n, int k, char board[MAX_N][MAX_N]) {count = 0;backtrack(board, 0, n, k);return count;
}int main() {int n, k;char board[MAX_N][MAX_N];while (scanf("%d %d", &n, &k) == 2) {if (n == -1 && k == -1) {break;}for (int i = 0; i < n; i++) {scanf("%s", board[i]);}int result = chessboard(n, k, board);printf("%d\n", result);}return 0;
}
该算法使用回溯法的思想,通过递归地尝试在每个位置放置棋子,同时检查放置的位置是否满足要求。首先,定义isValid函数用于检查某个位置是否合法,即同一行、同一列以及对角线上没有其他棋子。然后,使用backtrack函数进行回溯搜索,从左到右、从上到下依次尝试在每个位置放置棋子。如果当前位置合法,就将棋子放置在该位置,并继续在下一列进行回溯搜索。如果当前位置不合法,则继续在下一行尝试。当回溯到最后一列时,如果已经放置了k个棋子,则找到了一个可行的摆放方案,将计数器加1。最后,调用chessboard函数进行求解,并输出可行的摆放方案数目C。
第3题:课程表
现在你总共有n门课需要选,记为0到n-1。在选修某些课程之前需要一些先修课程。例如,想要学习课程0,你需要先完成课程1,我们用一个匹配来表示他们:[0, 1]。给定课程总量以及它们的先决条件,判断是否可能完成所有课程的学习?
时间限制:1000
内存限制:65536
输入
多组数据。每组数据第一行是n和m,n表示有n门课程,m表示有m组依赖关系,接下来的m行是依赖关系的具体信息a b,表示第a门课程依赖第b门课程。 0<=n <=1000,0 <= m <= 4000 两组数据之间可能有空行
输出
对每组数据,能完成输出 True,不能完成输出 False
样例输入
2 1
1 0
2 2
1 0
0 1
样例输出
True
False
提示
示例2解释: 总共有2门课程。学习课程1之前,你需要先完成课程0;并且学习课程0之前,你还应先完成课程1。这是不可能的。
对于课程表问题,使用搜索剪枝技术是一个有效的方法。我们可以使用深度优先搜索(DFS)来遍历课程的依赖关系,并在搜索过程中进行剪枝以提高效率。
以下是使用搜索剪枝技术来解决课程表问题的C语言代码:
#include <stdio.h>
#include <stdbool.h>#define MAX_N 1000
#define MAX_M 4000bool dfs(int course, int numCourses, int prerequisites[MAX_M][2], int numPrerequisites, bool visited[MAX_N], bool path[MAX_N]) {visited[course] = true; // 标记当前课程为已访问path[course] = true; // 将当前课程加入遍历路径中// 遍历当前课程的后续课程for (int i = 0; i < numPrerequisites; i++) {if (prerequisites[i][1] == course) {int nextCourse = prerequisites[i][0];// 判断是否存在环路,即当前课程在当前的遍历路径中if (path[nextCourse]) {return false;}// 如果后续课程未访问,则继续进行深度优先搜索if (!visited[nextCourse]) {if (!dfs(nextCourse, numCourses, prerequisites, numPrerequisites, visited, path)) {return false;}}}}path[course] = false; // 将当前课程从遍历路径中移除return true;
}bool canFinish(int numCourses, int prerequisites[MAX_M][2], int numPrerequisites) {bool visited[MAX_N] = {false}; // 记录课程是否已访问bool path[MAX_N] = {false}; // 记录当前的遍历路径// 对每门课程进行深度优先搜索for (int i = 0; i < numCourses; i++) {if (!visited[i]) {if (!dfs(i, numCourses, prerequisites, numPrerequisites, visited, path)) {return false;}}}return true;
}int main() {int numCourses, numPrerequisites;int prerequisites[MAX_M][2];while (scanf("%d %d", &numCourses, &numPrerequisites) == 2) {if (numCourses == 0 && numPrerequisites == 0) {break;}for (int i = 0; i < numPrerequisites; i++) {scanf("%d %d", &prerequisites[i][0], &prerequisites[i][1]);}bool result = canFinish(numCourses, prerequisites, numPrerequisites);printf("%s\n", result ? "True" : "False");}return 0;
}
该算法使用深度优先搜索(DFS)进行遍历,通过递归地搜索课程的依赖关系。首先,定义dfs函数进行深度优先搜索,其中course表示当前的课程,visited用于记录课程是否已访问,path用于记录当前的遍历路径。在搜索过程中,首先将当前课程标记为已访问,并将其加入遍历路径中。然后,遍历当前课程的后续课程,如果发现后续课程已经在当前的遍历路径中,则表示存在环路,返回false。如果后续课程未访问,则继续进行深度优先搜索。最后,将当前课程从遍历路径中移除,并返回true表示搜索完成。在canFinish函数中,对每门课程进行深度优先搜索,如果存在环路,则返回false;如果所有课程都能够完成搜索,返回true。最后,调用canFinish函数进行求解,并输出结果。
第4题:拯救公主
多灾多难的公主又被大魔王抓走啦!国王派遣了第一勇士阿福去拯救她。
身为超级厉害的术士,同时也是阿福的好伙伴,你决定祝他一臂之力。你为阿福提供了一张大魔王根据地的地图,上面标记了阿福和公主所在的位置,以及一些不能够踏入的禁区。你还贴心地为阿福制造了一些传送门,通过一个传送门可以瞬间转移到任意一个传送门,当然阿福也可以选择不通过传送门瞬移。传送门的位置也被标记在了地图上。此外,你还查探到公主所在的地方被设下了结界,需要集齐K种宝石才能打开。当然,你在地图上也标记出了不同宝石所在的位置。
你希望阿福能够带着公主早日凯旋。于是在阿福出发之前,你还需要为阿福计算出他最快救出公主的时间。
地图用一个R×C的字符矩阵来表示。字符S表示阿福所在的位置,字符E表示公主所在的位置,字符#表示不能踏入的禁区,字符$表示传送门,字符.表示该位置安全,数字字符0至4表示了宝石的类型。阿福每次可以从当前的位置走到他上下左右四个方向上的任意一个位置,但不能走出地图边界。阿福每走一步需要花费1个单位时间,从一个传送门到达另一个传送门不需要花费时间。当阿福走到宝石所在的位置时,就视为得到了该宝石,不需要花费额外时间。
时间限制:1000
内存限制:65536
输入
第一行是一个正整数T(1 <= T <= 10),表示一共有T组数据。 每一组数据的第一行包含了三个用空格分开的正整数R、C(2 <= R, C <= 200)和K,表示地图是一个R×C的矩阵,而阿福需要集齐K种宝石才能够打开拘禁公主的结界。 接下来的R行描述了地图的具体内容,每一行包含了C个字符。字符含义如题目描述中所述。保证有且仅有一个S和E。$的数量不超过10个。宝石的类型在数字0至4范围内,即不会超过5种宝石。
输出
对于每一组数据,输出阿福救出公主所花费的最少单位时间。若阿福无法救出公主,则输出“oop!”(只输出引号里面的内容,不输出引号)。每组数据的输出结果占一行。
样例输入
1
7 8 2
…
…S…#0.
.##…1…
.0#…
…1#…
…##E…
…1…
样例输出
11
根据题目要求,我们可以使用贪心算法来解决这个问题。贪心算法的思想是每一步都选择当前最优的解决方案,希望最终能够得到全局最优解。
下面是使用贪心算法解决该问题的C语言代码示例:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>#define MAX_ROWS 200
#define MAX_COLS 200int minTime; // 最少单位时间
int gemsCollected; // 已经收集到的宝石数量
char map[MAX_ROWS][MAX_COLS];
int visited[MAX_ROWS][MAX_COLS];
int rows, cols, requiredGems;
int startRow, startCol, endRow, endCol; // 起始位置和目标位置的行列坐标
int gems[MAX_ROWS][MAX_COLS]; // 记录宝石的类型// 计算两点之间的曼哈顿距离
int manhattanDistance(int row1, int col1, int row2, int col2) {return abs(row1 - row2) + abs(col1 - col2);
}// 贪心算法
void greedy(int row, int col, int time) {// 边界条件判断if (row < 0 || row >= rows || col < 0 || col >= cols || visited[row][col] || map[row][col] == '#')return;// 标记当前位置为已访问visited[row][col] = 1;// 到达目标位置,更新最少单位时间if (row == endRow && col == endCol) {if (gemsCollected == requiredGems) {if (time < minTime || minTime == -1)minTime = time;}visited[row][col] = 0; // 恢复当前位置为未访问状态return;}// 如果当前位置是宝石,则增加宝石数量if (gems[row][col] != -1)gemsCollected++;// 向四个方向进行搜索greedy(row - 1, col, time + 1); // 上greedy(row + 1, col, time + 1); // 下greedy(row, col - 1, time + 1); // 左greedy(row, col + 1, time + 1); // 右// 如果当前位置是宝石,则减少宝石数量if (gems[row][col] != -1)gemsCollected--;// 恢复当前位置为未访问状态visited[row][col] = 0;
}int main() {int numCases;scanf("%d", &numCases);while (numCases--) {scanf("%d %d %d", &rows, &cols, &requiredGems);// 初始化minTime = -1;gemsCollected = 0;// 读取地图数据for (int i = 0; i < rows; i++) {scanf("%s", map[i]);for (int j = 0; j < cols; j++) {visited[i][j] = 0;if (map[i][j] == 'S') {startRow = i;startCol = j;} else if (map[i][j] == 'E') {endRow = i;endCol = j;} else if (map[i][j] >= '0' && map[i][j] <= '4') {gems[i][j] = map[i][j] - '0';} else {gems[i][j] = -1;}}}// 计算起始位置到每个宝石的曼哈顿距离int gemDistances[5];memset(gemDistances, 0, sizeof(gemDistances));for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (gems[i][j] != -1) {int distance = manhattanDistance(startRow, startCol, i, j);if (gemDistances[gems[i][j]] == 0 || distance < gemDistances[gems[i][j]]) {gemDistances[gems[i][j]] = distance;}}}}// 根据宝石的曼哈顿距离进行排序for (int i = 0; i < requiredGems; i++) {int minDistance = -1;int minGem = -1;for (int j = 0; j < 5; j++) {if (gemDistances[j] != 0 && (minDistance == -1 || gemDistances[j] < minDistance)) {minDistance = gemDistances[j];minGem = j;}}gemDistances[minGem] = 0;for (int j = 0; j < rows; j++) {for (int k = 0; k < cols; k++) {if (gems[j][k] == minGem) {gems[j][k] = i;}}}}// 使用贪心算法搜索最短路径greedy(startRow, startCol, 0);// 输出结果if (minTime != -1) {printf("%d\n", minTime);} else {printf("oop!\n");}}return 0;
}
这个代码使用了深度优先搜索和贪心算法来解决问题,首先计算起始位置到每个宝石的曼哈顿距离,然后按照宝石的距离进行排序,然后使用贪心算法进行搜索,直到达到目标位置并且收集到足够数量的宝石。如果无法救出公主,则输出"oop!"。
请注意,这只是一个示例代码,可能还有一些边界情况没有考虑到,你可以根据实际情况进行修改和优化。
相关文章:

2021年12月 C/C++(五级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:书架 John最近买了一个书架用来存放奶牛养殖书籍,但书架很快被存满了,只剩最顶层有空余。 John共有N头奶牛(1 ≤ N ≤ 20,000),每头奶牛有自己的高度Hi(1 ≤ Hi ≤ 10,000),N头奶牛的总高度为S。书架高度为B(1 ≤…...

解决 git clone 时出现Failed to connect to 127.0.0.1 port 1573问题
今天去拉一个仓库代码,往常都是一下就拉下来了,今天却报错,报错信息如下: 原因:这种情况是因为代理在git中配置的,但是本身环境就有SSL协议了,所以取消git的https或者http代理即可 方法如下&…...
日本核污染水排海,有必要囤盐吗?
据央视新闻24日报道,当地时间8月24日13时,日本福岛第一核电站启动污水排海。消息一出,全球哗然。虽然事情已经过去了几天,但是,随着这一举动,大家就乱了阵脚,恐惧者有之,辱骂者有之&…...

windows 10自带命令查看文件的哈希值
windows的powershell自带了查看文件哈希值的命令: Get-FileHash 文件名 -Algorithm MD5/SHA1/SHA256 【案例】 查看文件的MD5值: 查看文件的SHA1值: 查看文件的SHA256值:...
ssm+vue理发店会员管理系统源码和论文
ssmvue理发店会员管理系统源码和论文089 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 网络技术和计算机技术发展至今,已经拥有了深厚的理论基础,并在现实中进行了充分运用&a…...

Python的for循环
for语法: """ for 临时变量 in 待处理数据集(序列):循环满足条件时执行的代码 """ 例子: name "itheima is a brand of itcast" count 0 for i in name:if i "a":count 1 print(f"a的数量…...
爬虫逆向实战(二十七)--某某招标投标网站招标公告
一、数据接口分析 主页地址:某网站 1、抓包 通过抓包可以发现数据接口是page 2、判断是否有加密参数 请求参数是否加密? 通过查看“载荷”模块可以发现,请求参数是一整个密文 请求头是否加密? 无响应是否加密? 通…...

线程和之间的通讯方式、进程之间的通讯方式、线程之间如何同步
通信是指线程之间以何种机制来交换信息,同步是指程序中用于控制不同线程间操作发生相对顺序的机制 进程由线程组成,所以进程中有的通讯机制线程中全都有 线程的通讯方式: 1. 锁机制:包括互斥锁、条件变量、读写锁 互斥锁提供了以…...
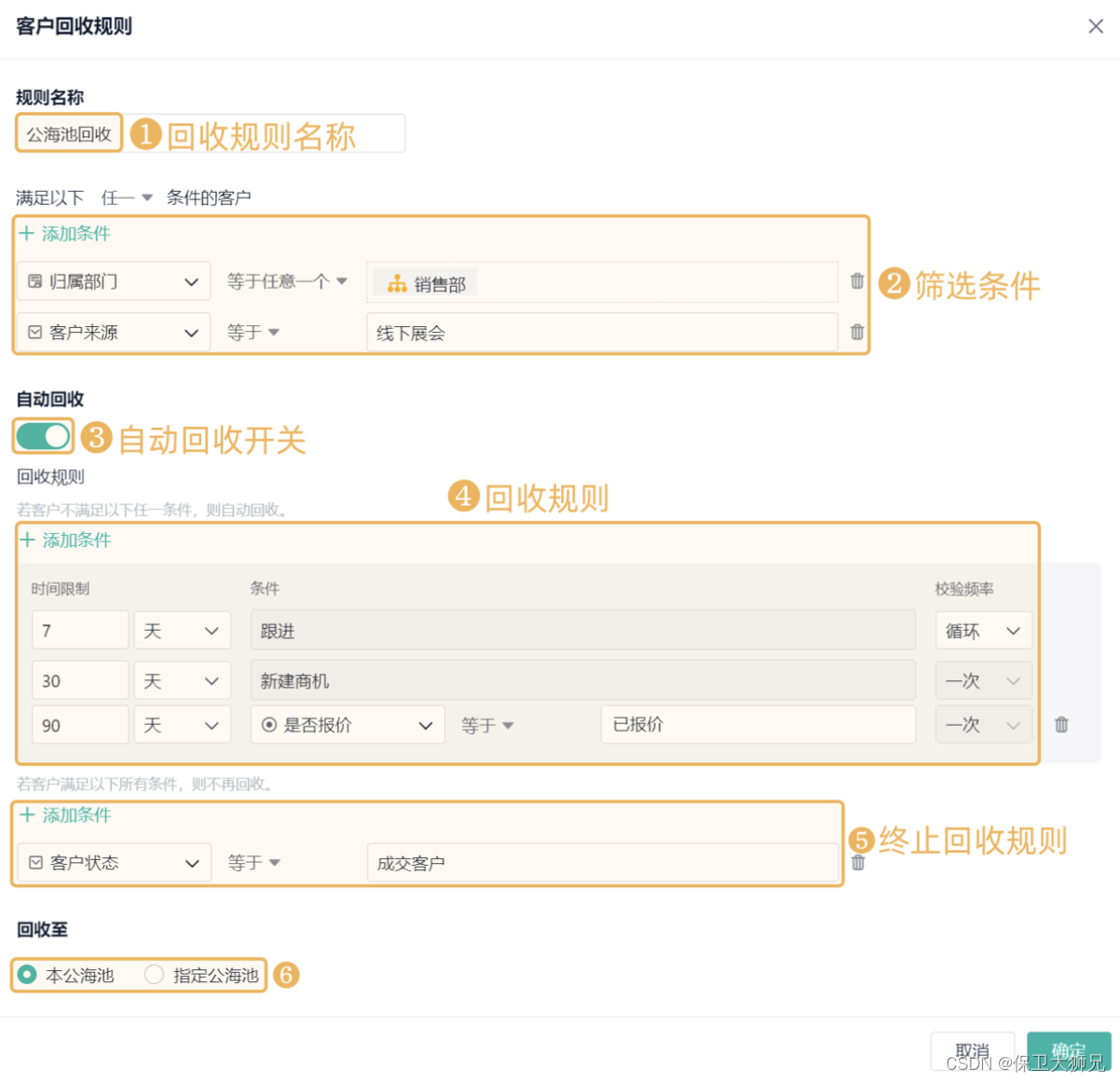
CRM线索公海如何管理?
对于销售和CRM客户管理而言,公海线索的管理极为重要,今天本文将告诉大家: 1、如何合理设置公海线索规则和流程?2、手把手教你完成公海管理系统的搭建 关于CRM的公海管理问题,需要根据企业的具体情况和销售流程来设置…...
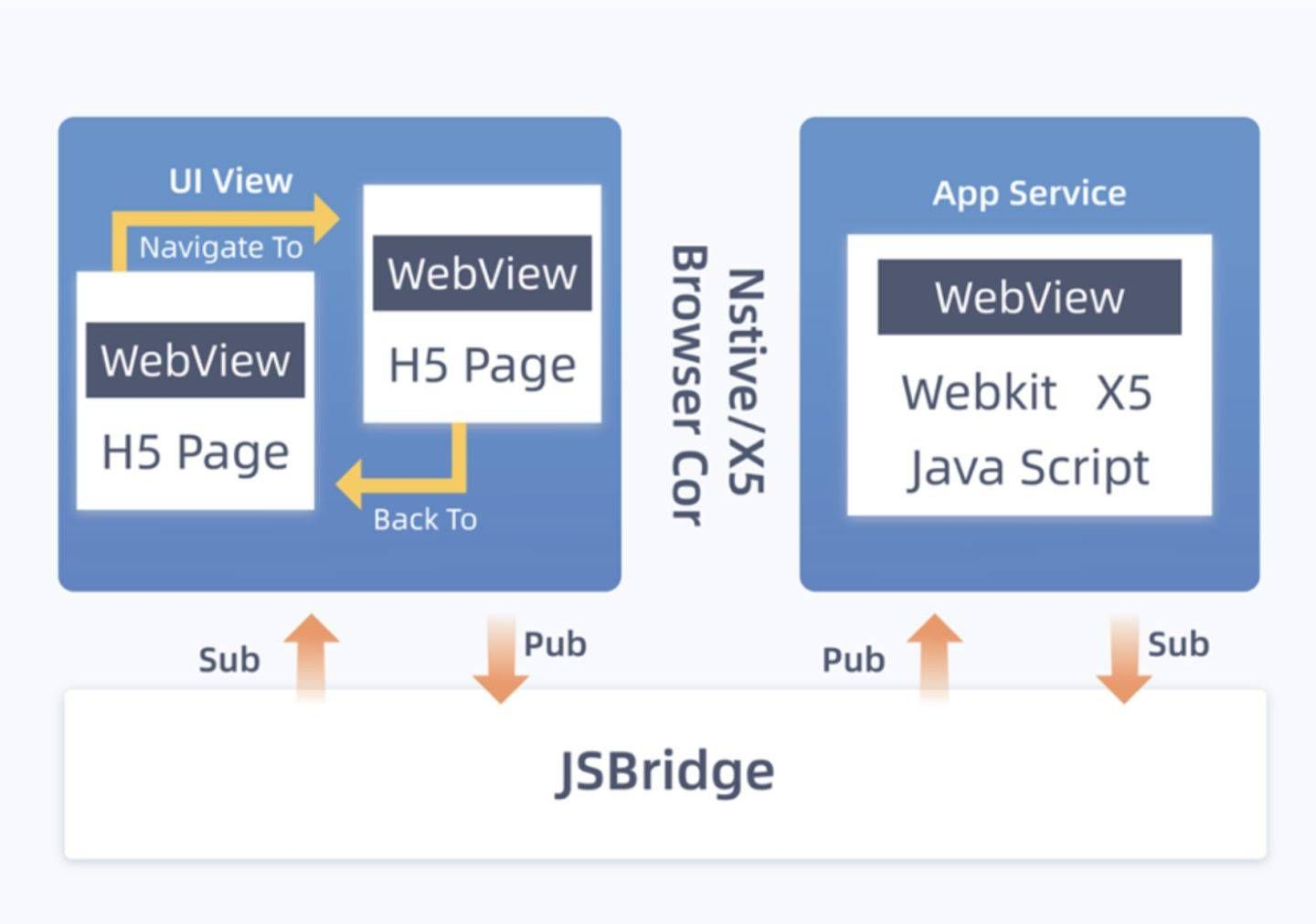
创建web应用程序,React和Vue怎么选?
React和Vue都是创建web应用程序的绝佳选择。React得到了科技巨头和庞大的开源社区的支持,代码库可以很大程度地扩展,允许你创建企业级web应用程序。React拥有大量合格甚至优秀的开发人员粉丝,可以解决你在开发阶段可能遇到的任何问题。 毫无疑…...
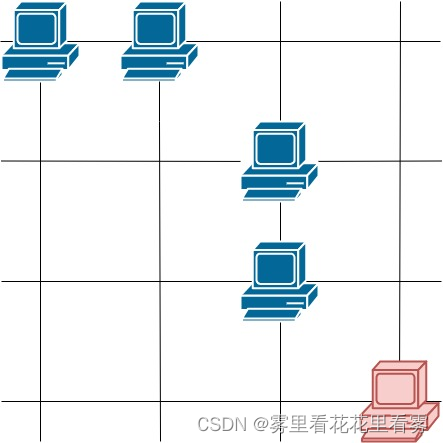
【每日一题】1267. 统计参与通信的服务器
【每日一题】1267. 统计参与通信的服务器 1267. 统计参与通信的服务器题目描述解题思路 1267. 统计参与通信的服务器 题目描述 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有…...

Python入门教程29:字符串前加r、u、b、f是什么意思?
★★★★★博文原创不易,我的博文不需要打赏,也不需要知识付费,可以白嫖学习编程小技巧,喜欢的老铁可以多多帮忙点赞,小红牛在此表示感谢。★★★★★ 关键字参数字符串前加上r、u、b和f,分别表示不同的字…...

java8 IntStream.range
简介 IntStream.range是Java 8中的一个方法,它是java.util.stream.IntStream类中的静态方法。这个方法用于生成一个顺序排列的整数流,包含起始值但不包含结束值。可以使用以下代码调用IntStream.range方法: IntStream.range(int startInclu…...
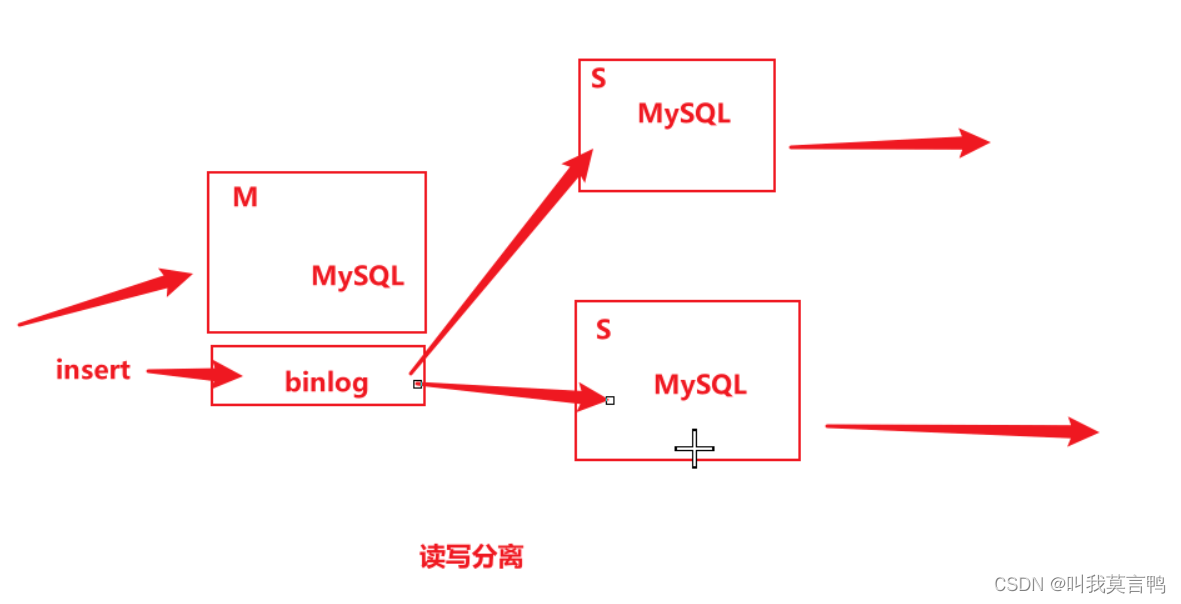
数据库集群的简单了解
Update 关于操作的日志 1.0 redo log 读一次写一次 一共2次, 不安全 注意redo log是顺写 而file是随机 所以Mysql做出类似HDFS的操作 行为日志和数据分离,但是不同的是,Mysql在内存中操作修改,如果不出事故,由内存中的行为来直接…...

CSS中如何实现文字阴影效果(text-shadow)?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 实现思路⭐ 示例⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣、刚刚踏入前…...
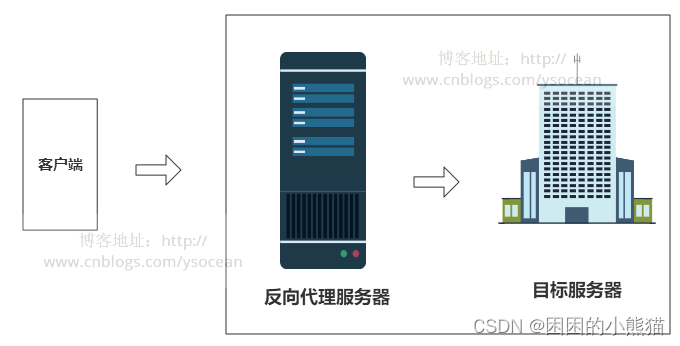
Nginx从入门到精通(超级详细)
文章目录 一、什么是Nginx1、正向代理2、反向代理3、负载均衡4、动静分离 二、centos7环境安装Nginx1、安装依赖2、下载安装包3、安装4、启动5、停止 三、Nginx核心基础知识1、nginx核心目录2、常用命令3、默认配置文件讲解4、Nginx虚拟主机-搭建前端静态服务器5、使用nignx搭建…...

为何反射探针关闭Mipmap后变成了白图
1)为何反射探针关闭Mipmap后变成了白图 2)2021.3 Android从AssetBundle中加载视频播放失败问题 3)SBP是否可以解决打包时FBX等模型文件中额外的GameObject 4)Addressables加载已打包过的Prefab后Mono脚本丢失 这是第349篇UWA技术知…...

成都睿趣科技:抖音开网店前期的流程是什么
随着互联网的快速发展,电子商务成为了商业领域中的一大利器,而在电商领域中,抖音作为一个强大的平台,也吸引了众多商家的目光。然而,要在抖音上开设一家成功的网店,并不是一件简单的事情,需要经…...

机房安全之道:构筑坚固的网络防线
引言: 在数字化时代,机房成为了许多组织和企业的核心基础设施,承载着重要的数据和应用。然而,随着网络攻击日益猖獗,机房的安全性显得尤为重要。本文将深入探讨如何构建坚固的网络防线,保护机房免受攻击的方…...

使用GoLand进行远程调试
对部署进行配置 在此配置远程服务器地址,映射,是否自动上传(更新)等 选择SFTP类型 选择上传 另外给自动上传选项打钩 此时在本地修改某个文件,远程机器相应目录的文件,也会被同步修改 对远程调试进行配置 远程机器需要安装delve 而…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
