2023年高教社杯数学建模思路 - 案例：异常检测

赛题思路

（赛题出来以后第一时间在CSDN分享）

https://blog.csdn.net/dc_sinor?type=blog

一、简介 – 关于异常检测

异常检测（outlier detection）在以下场景：

• 数据预处理
• 病毒木马检测
• 工业制造产品检测
• 网络流量检测

等等，有着重要的作用。由于在以上场景中，异常的数据量都是很少的一部分，因此诸如：SVM、逻辑回归等分类算法，都不适用，因为：

监督学习算法适用于有大量的正向样本，也有大量的负向样本，有足够的样本让算法去学习其特征，且未来新出现的样本与训练样本分布一致。

以下是异常检测和监督学习相关算法的适用范围：

异常检测

• 信用卡诈骗
• 制造业产品异常检
• 数据中心机器异常检
• 入侵检测

监督学习

• 垃圾邮件识别
• 新闻分类

二、异常检测算法

import tushare
from matplotlib import pyplot as pltdf = tushare.get_hist_data("600680")
v = df[-90: ].volume
v.plot("kde")
plt.show()

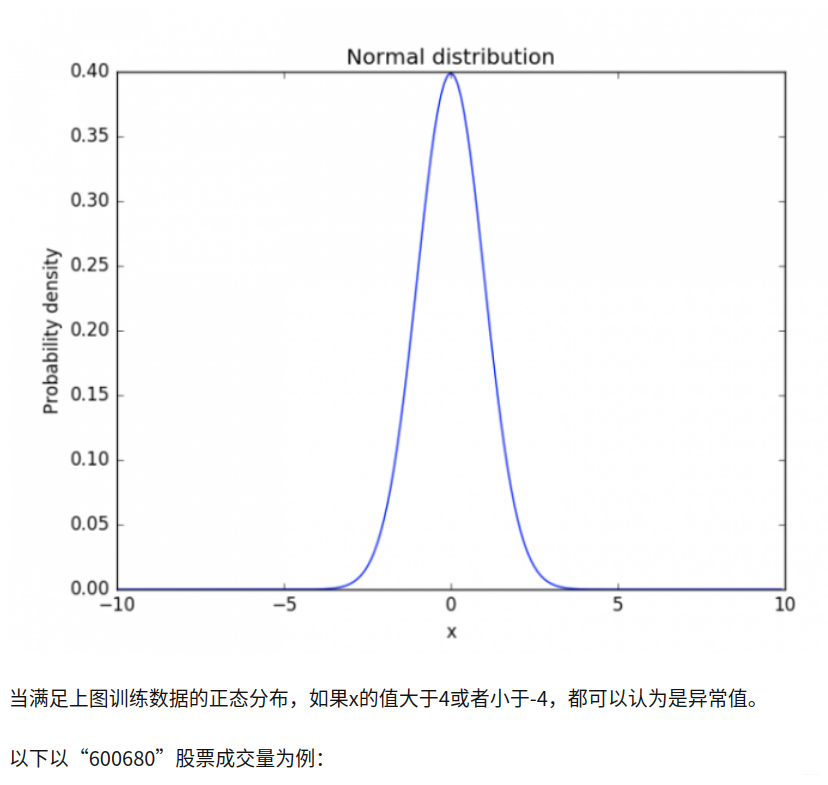
近三个月，成交量大于200000就可以认为发生了异常（天量，嗯，要注意风险了……）

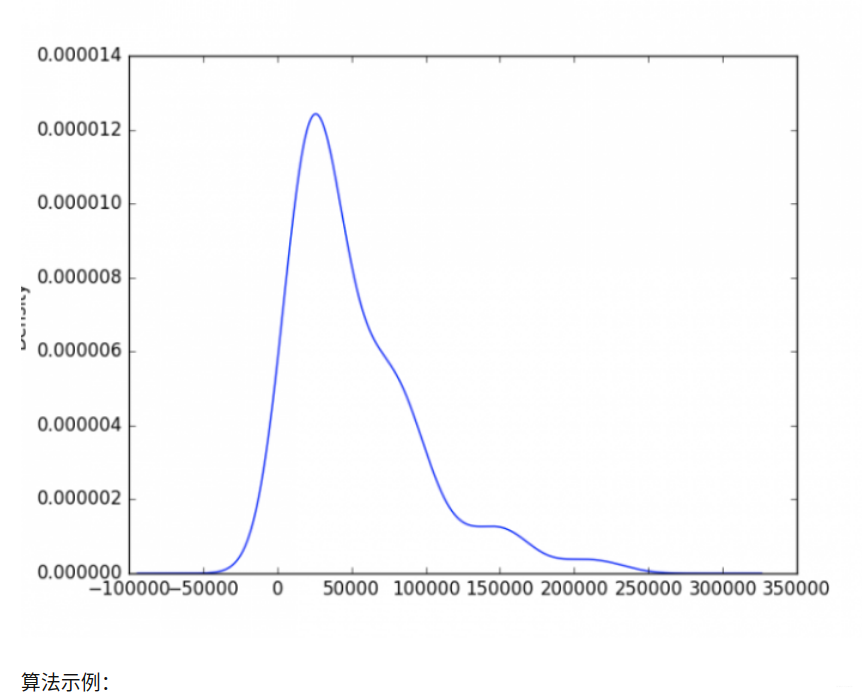
2. 箱线图分析

import tushare
from matplotlib import pyplot as pltdf = tushare.get_hist_data("600680")
v = df[-90: ].volume
v.plot("kde")
plt.show()

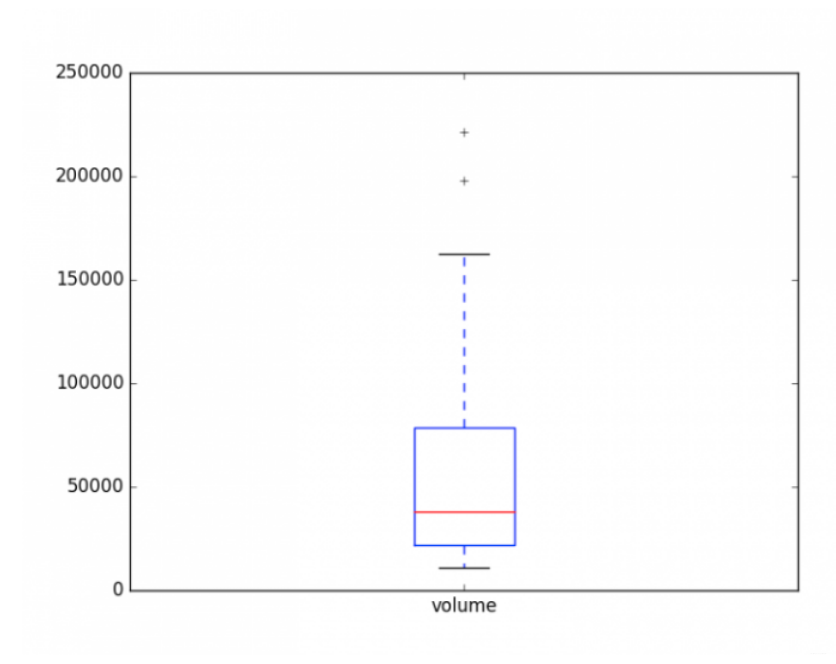
大体可以知道，该股票在成交量少于20000，或者成交量大于80000，就应该提高警惕啦！

3. 基于距离/密度

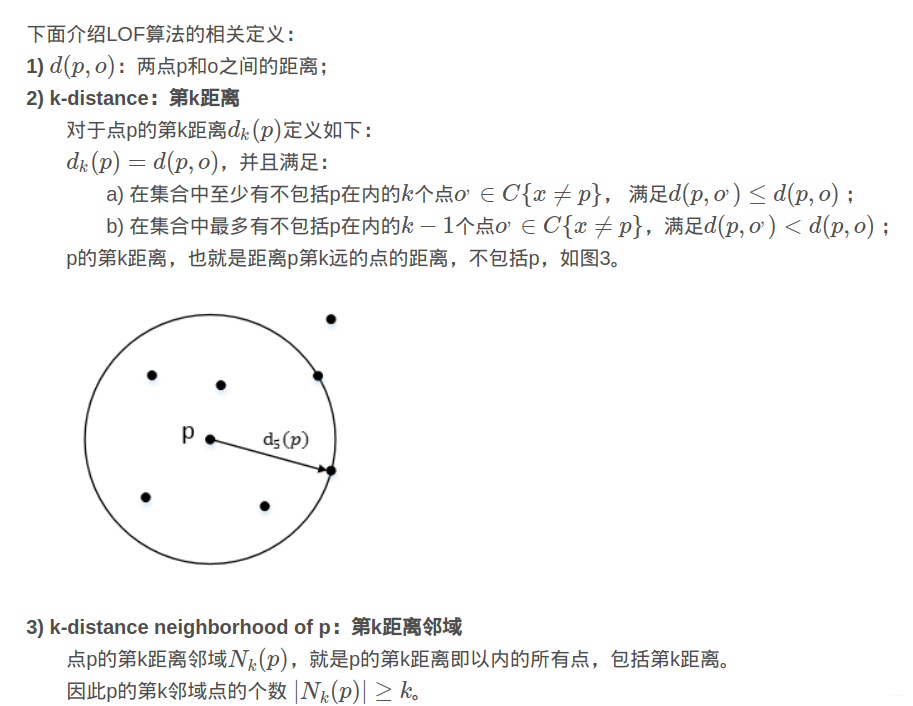
典型的算法是：“局部异常因子算法-Local Outlier Factor”，该算法通过引入“k-distance，第k距离”、“k-distance neighborhood，第k距离邻域”、“reach-distance，可达距离”、以及“local reachability density，局部可达密度 ”和“local outlier factor，局部离群因子”，来发现异常点。

用视觉直观的感受一下，如图2，对于C1集合的点，整体间距，密度，分散情况较为均匀一致，可以认为是同一簇；对于C2集合的点，同样可认为是一簇。o1、o2点相对孤立，可以认为是异常点或离散点。现在的问题是，如何实现算法的通用性，可以满足C1和C2这种密度分散情况迥异的集合的异常点识别。LOF可以实现我们的目标。

4. 基于划分思想

典型的算法是 “孤立森林，Isolation Forest”，其思想是：

假设我们用一个随机超平面来切割（split）数据空间（data space）, 切一次可以生成两个子空间（想象拿刀切蛋糕一分为二）。之后我们再继续用一个随机超平面来切割每个子空间，循环下去，直到每子空间里面只有一个数据点为止。直观上来讲，我们可以发现那些密度很高的簇是可以被切很多次才会停止切割，但是那些密度很低的点很容易很早的就停到一个子空间了。

这个的算法流程即是使用超平面分割子空间，然后建立类似的二叉树的过程：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForestrng = np.random.RandomState(42)# Generate train data
X = 0.3 * rng.randn(100, 2)
X_train = np.r_[X + 1, X - 3, X - 5, X + 6]
# Generate some regular novel observations
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 1, X - 3, X - 5, X + 6]
# Generate some abnormal novel observations
X_outliers = rng.uniform(low=-8, high=8, size=(20, 2))# fit the model
clf = IsolationForest(max_samples=100*2, random_state=rng)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)# plot the line, the samples, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-8, 8, 50), np.linspace(-8, 8, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.title("IsolationForest")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red')
plt.axis('tight')
plt.xlim((-8, 8))
plt.ylim((-8, 8))
plt.legend([b1, b2, c],["training observations","new regular observations", "new abnormal observations"],loc="upper left")
plt.show()

建模资料

资料分享: 最强建模资料