零知识证明(zk-SNARK)(一)
全称为 Zero-Knowledge Succinct Non-Interactive Argument of Knowledge,简洁非交互式零知识证明,简洁性使得运行该协议时,即便statement非常大,它的proof大小也仅有几百个bytes,并且验证一个proof的时间可以达到毫秒级别。
主要解决的场景就是,Prover 向 Verifier 证明某个共同认可的计算难题的计算结果是正确的,需要零知识,不能泄露任何信息。
核心方法是通过R1CS,QAP等方法将计算难题变为多项式,将计算结果正确性巧妙转化为了多项式的有特殊解的问题,生成对应proof,然后再运用多项式证明方法,来完成证明与验证。
Non-Interactive Argument of Knowledge of a Polynomial
(注意 计算和参数选取是在域内,即有模运算)
一般多项式的证明
场景如下:Verifier 有一个多项式 f ( x ) f(x) f(x),Prover 向 Verifer 证明他知道这一个多项式。
假设 Prover 知道的多项式为 p ( x ) p(x) p(x),那么现在要证明的就是 f ( x ) = p ( x ) f(x)=p(x) f(x)=p(x),如果这两个多项式的阶数最高为 d d d,那么两个多项式代表的曲线将最多有 d d d个交点,当 Verifier 随机在一个很大的范围内取一个值 s s s的时候,那么 s s s和 d d d相同的概率会非常低,所以有以下协议
- Verifier 在大范围里随机选择一个值 s s s,并且在本地计算 f ( s ) f(s) f(s),然后把 s s s发送给 Prover
- Prover 计算 p ( s ) p(s) p(s),然后发送给Verifier
- Verifier 验证 f ( s ) = ? p ( s ) f(s)\overset{?}=p(s) f(s)=?p(s)
证明多项式的根
有些多项式是可以分解多个多项式的乘积的,如假设 p ( x ) = ( x − a ) ( x − b ) ( x − c ) p(x)=(x-a)(x-b)(x-c) p(x)=(x−a)(x−b)(x−c)那么
假设 Prover 有一个多项式 p ( x ) p(x) p(x),现在他想证明他的多项式持有一部分根(部分多项式),也就是证明他的多项式 p ( x ) = t ( x ) h ( x ) p(x)=t(x)h(x) p(x)=t(x)h(x)中包含 t ( x ) t(x) t(x)假设为 ( x − a ) ( x − b ) (x-a)(x-b) (x−a)(x−b),而此时的 t ( x ) t(x) t(x)称为目标多项式,是公开的,要注意 Prover 是不能透露原多项式的。那么有以下协议
- Verifier 在大范围内随机取值 s s s,计算 t = t ( s ) t= t(s) t=t(s),然后将 s s s发送给 Prover
- Proer 计算 h ( x ) = p ( x ) t ( x ) h( x) = \frac {p(x)}{t(x)} h(x)=t(x)p(x), h ( s ) h(s) h(s), p ( s ) p(s) p(s),然后发送后两个给 Verifier
- Verfier 验证 p ( s ) = ? t ( s ) h ( s ) p(s)\overset{?}=t(s)h(s) p(s)=?t(s)h(s)
显而易见以上变量都局限为整数,如果 p p p确实能够整除 t t t,那么等式一定是成立的,如果不能,那么式子将存在余式,有极大的概率不是整数。
当然此协议仍然有很大漏洞,比如 Prover 可能完全不知道 p ( x ) p(x) p(x),但知道公开的 t ( x ) t(x) t(x),所以可以完全捏造出 h ( x ) h(x) h(x)满足条件。
同态加密
显然我们不能在协议里进行明文的传输,但又需要密文的计算,所以需要一个满足加密和计算两种特性的算法。
同态加密算法 E ( x ) E(x) E(x),如 E ( a x + b y ) = g a x + b y = g a x ⋅ g b y = ( g x ) a ⋅ ( g y ) b = E ( x ) a ⋅ E ( y ) b . E(a x+b y)=g^{a x+b y}=g^{a x} \cdot g^{b y}=\left(g^{x}\right)^{a} \cdot\left(g^{y}\right)^{b}=E(x)^{a} \cdot E(y)^{b} . E(ax+by)=gax+by=gax⋅gby=(gx)a⋅(gy)b=E(x)a⋅E(y)b.( g g g是生成元),这里基于离散对数难题和CDH假设(即给定 g a , g b g^a,g^b ga,gb,得到 g a b g^{ab} gab很困难)。显然这是仅仅满足同态加法的同态加密,不支持密文相乘。
那么该算法不支持乘法,仅有一个 s s s的情况下,该怎么同态计算多项式呢?显然是不行的,于是想办法把同态乘法转变为同态加法,注意到,多项式 P ( x ) P(x) P(x)可以看作是一组系数和未知数的线性结合,也就是计算出 s s s的各个幂次,这需要固定好多项式的阶数 d d d,相当于限制了多项式的阶数,这样提前计算出 s 1 , … , s d s^1,\dots,s^d s1,…,sd,然后计算出多项式的每个部分相加即可。
具体使用如下,
- Verifier 在大范围里随机选择一个 s s s,先计算好 s s s的幂次 s 1 , … , s d s^1,\dots,s^d s1,…,sd,接着计算 t ( s ) t(s) t(s),最后 E ( 1 ) , E ( s ) , … , E ( s d ) E(1),E(s),\dots,E(s^d) E(1),E(s),…,E(sd)并发给 Prover
- Prover 收到数据后计算, h ( x ) = p ( x ) t ( x ) h( x) = \frac {p(x)}{t(x)} h(x)=t(x)p(x),然后配合多项式的系数计算 E ( p ( s ) ) E(p(s)) E(p(s)), E ( h ( s ) ) E(h(s)) E(h(s))并发送给Verifier
- Verifier 进行验证 E ( p ( s ) ) = ? E ( t ( s ) ) E ( h ( s ) ) E(p(s))\overset{?}=E(t(s))E(h(s)) E(p(s))=?E(t(s))E(h(s)),即 g p ( s ) = ( g h ( s ) ) t ( s ) g^{p(s)} = (g^{h(s)})^{t(s)} gp(s)=(gh(s))t(s)
** KCA(The Knowledge of Coefficient Test and Assumption)**
上面的协议的仍然有很大漏洞,比如 Prover 在计算多项式的时候,没有采用多项式的格式(常数系数和未知数的线性组合),而是使用了另外的方法,算法找到一个满足 z p = ( z h ) t ( s ) z_p = (z_h)^{t(s)} zp=(zh)t(s)的两个值 z p , z h z_p,z_h zp,zh去替代掉 g p ( s ) , g h ( s ) g^{p(s)},g^{h(s)} gp(s),gh(s),也就是根本没用多项式,直接仿造了满足条件的结果。
这里就需要对 Prover 进行限制,让他必须使用满足条件的多项式,限定为常数,也限定了指数,不能随意改变指数。所以KCA也可以叫做KEA(Knowledge of exponent)
思路如下,
定义一对元素 ( a , b = α ⋅ a ) (a,b = \alpha \cdot a) (a,b=α⋅a)(称为一个 α \alpha α-对), α ⋅ a \alpha \cdot a α⋅a表示 α \alpha α个 a a a相加,也就是 a α a^\alpha aα,那么一个KC流程如下具体如下,
- 首先Verifier会随机选择一个非零的 α \alpha α,计算 b = α ⋅ a b = \alpha \cdot a b=α⋅a,显然这是一个 α − s h i f t \alpha -shift α−shift。
- Verifier 发送这个 challenge pair ( a , b ) (a,b) (a,b)给 Prover。
- 这时候 Prover 会 respond 一对不一样,但具有相同性质的 pair ( a ′ , b ′ ) (a',b') (a′,b′),它应当是 α − s h i f t \alpha -shift α−shift
- 如果收到的是一个 α − s h i f t \alpha -shift α−shift,那么Verifier 接受这个response
注意,这是满足DL问题的, Prover 是很难找到一个 α \alpha α,那么她该如何构造新的 α − s h i f t \alpha -shift α−shift呢?一个显而易见的方式是,Prover 选择一个常数系数 γ \gamma γ,直接构造 ( a ′ , b ′ ) = γ ( a , b ) (a',b') = \gamma(a,b) (a′,b′)=γ(a,b)。
假设 Verifier 发送的不是一个,而是是 d d d组 α − s h i f t \alpha -shift α−shift,那么 Prover 也将选择一组系数 c 1 , … , c d c_1,\dots,c_d c1,…,cd,respond 一个
( a ′ , b ′ ) = ( ∑ i = 1 d c i a i , ∑ i = 1 d c i b i ) (a',b') = (\sum_{i=1}^d c_ia_i,\sum_{i=1}^d c_ib_i) (a′,b′)=(∑i=1dciai,∑i=1dcibi),显然该对也是满足 α − s h i f t \alpha -shift α−shift。如果把 Verifier 发的内容优化一下,就构成了KCA。
Blind Evaluation of Polynomials Verifiable Protocol
完整的多项式盲验证协议。
解决整个问题需要满足的两个性质:
- **Blindness:**也就是 Prover 不能获取到 s s s,同样 Verifier 也不能拿到 p ( x ) p(x) p(x)(同态)。
- **Verifiability:**也就是得确保 Prover 发的 E ( p ( x ) ) E(p(x)) E(p(x))确实是用某个多项式 p ( x ) p(x) p(x)计算的,而不是完全不相关的数据(KCA)
那么使用KCA对前面协议进行优化如下,
- Verifier 随机选择 α \alpha α(非0)和 s s s,然后计算 t ( s ) t(s) t(s),接着构造 α − s h i f t \alpha -shift α−shift ( g , g α ) , ( g s , g α ⋅ s ) , … , ( g s d , g α ⋅ s d ) (g,g^{\alpha}),(g^s,g^{\alpha \cdot s} ),\dots,(g^{s^d},g^{\alpha \cdot s^d}) (g,gα),(gs,gα⋅s),…,(gsd,gα⋅sd)
- Prover 则使用多项式 p ( x ) p(x) p(x)的系数 c 1 , … , c d c_1,\dots,c_d c1,…,cd,然后计算 E ( h ( s ) ) E(h(s)) E(h(s))以及 ( E ( p ( s ) ) , E ( α p ( s ) ) ) = ( g ∑ i = 1 d c i s i , g ∑ i = 1 d c i α ⋅ s d ) (E(p(s)),E(\alpha p(s))) = (g^{\sum_{i=1}^d c_is^i},g^{\sum_{i=1}^d c_i\alpha \cdot s^d}) (E(p(s)),E(αp(s)))=(g∑i=1dcisi,g∑i=1dciα⋅sd),发送给Verifier
- Verifier进行验证 E ( p ( s ) ) = ? E ( α p ( s ) ) E(p(s))\overset ?=E(\alpha p(s)) E(p(s))=?E(αp(s))和 E ( p ( s ) ) = ? E ( t ( s ) ) E ( h ( s ) ) E(p(s))\overset{?}=E(t(s))E(h(s)) E(p(s))=?E(t(s))E(h(s))即可
该方案也可以解决前面的问题,即Prover 不能随意构造满足类似 z p = ( z h ) t ( s ) z_p = (z_h)^{t(s)} zp=(zh)t(s)的 h ( s ) h(s) h(s),这样会很容易不满足 α − s h i f t \alpha -shift α−shift的限制条件。
Parings and bilinear map
前面的协议基本实现了诚实两方之间的交互方案,相关的 proof 仅仅在两方之间有效,无法重复使用,但在实际运用中,存在这恶意的多方的情况,这显然不符合实际。所以,需要让一些秘密参数变得可重复使用甚至公开,而且足够可信以防止滥用。
首先考虑将 Verifier 生成的 ( t ( s ) , α ) (t(s),\alpha) (t(s),α)进行加密保护,防止泄露。如果采用前面的同态加密,那么在后面的乘法计算中就会涉及到同态的乘法 ,但是前面用的同态算法不支持同态乘法。那么必须用到类似乘法的时候应该怎么办呢?这时候就引入了椭圆双曲线映射。
Parings 是能够将一个集合里的两个加密输入确定性的映射到另一个集合里的一个输出的一种乘法表示函数。
即: e : G × G → G T e: \mathbb{G} \times \mathbb{G} \rightarrow \mathbb{G}_T e:G×G→GT满足以下性质
e ( g 1 a , g 2 b ) = e ( g 1 , g 2 ) a b = e ( g 1 a b , g 2 ) = e ( g 1 , g 2 a b ) \begin{aligned}e(\mathrm{g_1^a,g_2^b})&=\mathrm{e(g_1,g_2)^{ab}=e(g_1^{ab},g_2)=e(g_1,g_2^{ab})}\end{aligned} e(g1a,g2b)=e(g1,g2)ab=e(g1ab,g2)=e(g1,g2ab)
e ( g 1 a , g 2 b ) e ( g 1 c , g 2 d ) = e ( g 1 , g 2 ) a b + c d \begin{aligned} e(\mathrm{g_1^a,g_2^b})e(\mathrm{g_1^c,g_2^d})&=\mathrm{e(g_1,g_2)^{ab+cd}}\end{aligned} e(g1a,g2b)e(g1c,g2d)=e(g1,g2)ab+cd
其意义在于,将某个群中的一对元素映射到一个新的群,当且仅当两个原像对应指数的积相同其像也相同。并且,该函数要求是可计算的(即不需要用暴力搜索等方式),它能够验证一对(加密后的)数据的乘积是否和另一对相同(虽然算不出这个乘积)
接下来将协议的计算放到满足Parings的椭圆曲线群上来。
Multiple Parties Composite Common Reference String
首先引入一个可信的第三方来随机生成 s s s和 α \alpha α,并且计算出CRS(Common Reference String),共证明和验证两部分,都是公开的( i ∈ { 0 , … , d } i \in \{0,\dots,d\} i∈{0,…,d}),接着需要删除掉 s s s和 α \alpha α。
- Proving Key: E ( s i ) , E ( α s i ) = g s i , g α s i E(s^i),E(\alpha s^i) = g^{s^i},g^{\alpha s^i} E(si),E(αsi)=gsi,gαsi
- Verification Key: E ( t ( s ) ) , E ( α ) = g t ( s ) , g α E(t(s)),E(\alpha) = g^{t(s)},g^{\alpha} E(t(s)),E(α)=gt(s),gα
接着基于CRS,让 Prover 和 Verifier 仅仅通过CRS就能完成协议。继续优化协议如下,(下面简化 p = p ( s ) , t , h p=p(s),t,h p=p(s),t,h也类似)
- 对于 Prover 来说,公开的CRS中已经包含了第一步的内容,接下来是利用 Proving Key 来计算出 E ( h ( s ) ) E(h(s)) E(h(s))和 ( E ( p ( s ) ) , E ( α p ( s ) ) ) (E(p(s)),E(\alpha p(s))) (E(p(s)),E(αp(s)))
- 对于Verifier来说,是利用CRS中的 Verfication来进行验证( p ′ = α p p' = \alpha p p′=αp)
- 首先验证 p = t ⋅ h p=t \cdot h p=t⋅h,即 e ( g p , g 1 ) = e ( g t , g h ) = e ( g , g ) p = e ( g , g ) t ⋅ h e(g^p,g^1) = e(g^t,g^h) = e(g,g)^p = e(g,g)^{t \cdot h} e(gp,g1)=e(gt,gh)=e(g,g)p=e(g,g)t⋅h
- 然后验证 α − s h i f t \alpha -shift α−shift,即 e ( g p , g α ) = e ( g p ′ , g ) e(g^p,g^\alpha) = e(g^{p'},g) e(gp,gα)=e(gp′,g)
注意:这里也暴露出两个问题,
- Proving Key 中的 E ( α ) E(\alpha) E(α)是公开的,也就是对于 Prover 来说 ,他是可以打破多项式的限制条件的。
- 引入了一个可信第三方,但更复杂的现实中不能保证第三方不存在恶意,比如不销毁 trusted setup 的随机秘密,这一旦暴露会导致任何人都可以伪造证明。
于是 ZKSNARK 引入了多方联合的setup,每个人用自己的私钥 ( α , s ) (\alpha,s) (α,s)和前一个人生成的 CRS 作为输入生成一个新的 CRS,只要保证有一个人销毁了私钥,就能保证最终的CRS是安全的。具体实现如下,
假设有三方 Alice,Bob,Carol 参与,仅需要使用同态乘法让每个人的私钥相加即可

当然这里敌手是可以对多个不同的 ( α , s ) (\alpha,s) (α,s)进行随机采样,提供随机数来加入到CRS中达到破坏有效性的目的。
那么如何验证最终CRS的一致性呢?采用的是前面的Paring,
检验 s s s:将 s 1 s^1 s1作为一个基准,验证方式如下,
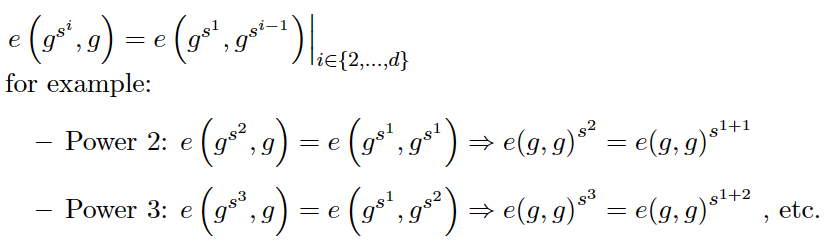
检验 α − s h i f t \alpha -shift α−shift:
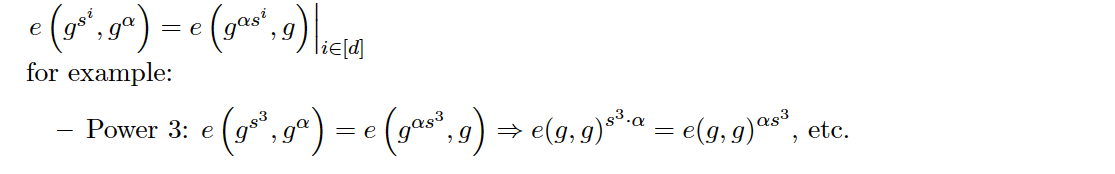
为了让参与方诚实的使用前面其他参与方的CRS,需要要求每个参与方( 除了第一个)将自己的秘密参数加密并公开,这样每个参与方就可以通过Paring来验证其他参与方是否诚实的进行了验证。如下,假设 Bob 公开
( g s B i , g α B , g α B s B i ) ∣ i ∈ [ d ] \left.\left(g^{s_B^i},g^{\alpha_B},g^{\alpha_Bs_B^i}\right)\right|_{i\in[d]} (gsBi,gαB,gαBsBi) i∈[d]
那么参与方 Alice 就可以验证
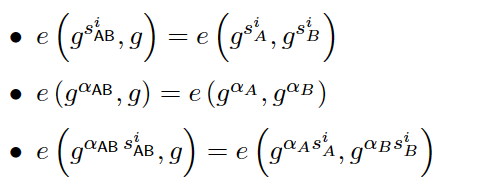
同理参与方 Carol 公开后也可以进行验证。
完整的简短非交互式的多项式证明方案
这里用 { g s i } i ∈ [ d ] \{g^{s^i}\}_{i\in[d]} {gsi}i∈[d]代表 s 1 , … , s d s^1,\dots,s^d s1,…,sd
首先确定好目标多项式 t ( x ) t(x) t(x)和 prover 的多项式的阶数 d d d,prover 需要证明他持有的多项式里含有 t ( x ) t(x) t(x)。
具体如下

参考
浅谈零知识证明:背景与起源
zcash官方科普
Exploring Elliptic Curve Pairings
Quadratic Arithmetic Programs: from Zero to Hero
Why and how zk-SNARK works
ZKSNARK介绍
李威翰,张宗洋,周子博等.简洁非交互零知识证明综述[J].密码学报,2022,9(03):379-447.DOI:10.13868/j.cnki.jcr.000525.
相关文章:

零知识证明(zk-SNARK)(一)
全称为 Zero-Knowledge Succinct Non-Interactive Argument of Knowledge,简洁非交互式零知识证明,简洁性使得运行该协议时,即便statement非常大,它的proof大小也仅有几百个bytes,并且验证一个proof的时间可以达到毫秒…...

linux中打印数据的行缓冲模式
1. 回车换行符在Window下和在Linux下的区别: 在Window下:回车换行符为\r\n 在Linux下:回车换行符为\n \n为换行符,换行相当于光标跳转到下一行的这个位置 \r为回车符,回车相当于光标跳转到当前行的最左边的位置 所以…...

香橙派OrangePi zero H2+ 驱动移远4G/5G模块
目录 1 安装系统和内核文件: 1.1 下载镜像 1.2 内核头安装 1.2.1 下载内核 1.2.2 将内核头文件导入开发板中 1.2.3 安装内核头 2 安装依赖工具: 2.1 Installing Required Host Utilities 3 驱动步骤: 3.1 下载模块驱动文件…...

自动驾驶——【规划】记忆泊车特殊学习路径拟合
1.Back ground 如上图,SLAM学习路线Start到End路径,其中曲线SDAB为D档位学习路径,曲线BC为R学习路径,曲线AE为前进档D档学习路径。 为了使其使用记忆泊车时,其驾驶员体验感好,需去除R档倒车部分轨迹&#x…...
)
【跟小嘉学 Rust 编程】十六、无畏并发(Fearless Concurrency)
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...
)
Android 进阶——图形显示系统之VSync和 Choreographer的创建详解(一)
引言 前一篇文章Android 进阶——图形显示系统之底层图像显示原理小结(一)介绍了关于Android 图形显示系统的基础理论,相信你对于Android的图形显示系统中图形界面渲染刷新机制有了更深的了解,接下来进一步讲解VSync和Choreography的联系和作用。 一、VSync 信号的产生概…...
SQL Server开启变更数据捕获(CDC)
一、CDC简介 变更数据捕获(Change Data Capture ,简称 CDC):记录 SQL Server 表的插入、更新和删除操作。开启cdc的源表在插入、更新和删除操作时会插入数据到日志表中。cdc通过捕获进程将变更数据捕获到变更表中,通过…...

八、性能测试
八、性能测试 8.1 性能测试代码 #include"ConcurrentAlloc.h"// ntimes 一轮申请和释放内存的次数 // rounds 轮次 void BenchmarkMalloc(size_t ntimes, size_t nworks, size_t rounds) {std::vector<std::thread> vthread(nworks);std::atomic<size_t&g…...

景芯SoC 芯片全流程培训
【全网唯一】景芯SoC是一款用于芯片全流程培训的低功耗ISP图像处理SoC,采用低功耗RISC-V处理器,内置ITCM SRAM、DTCM SRAM,集成包括MIPI、ISP、CNN、QSPI、UART、I2C、GPIO、百兆以太网等IP,采用SMIC40工艺设计流片。 培训数据包括…...
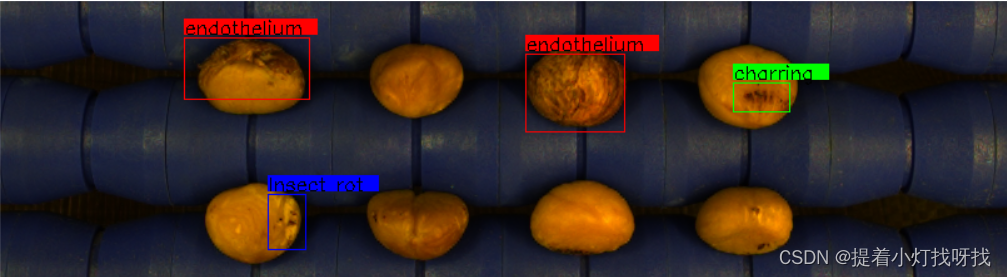
目标检测后的图像上绘制边界框和标签
效果如图所示,有个遗憾就是CV2在图像上显示中文有点难,也不想用别的了,所以改成了英文,代码在下面了,一定要注意一点,就是标注文件的读取一定要根据自己的实际情况改一下,我的所有图像的标注文件…...

Leetcode: 1. 两数之和 【题解超详细】
前言 有人夜里挑灯看花,有人相爱,有人夜里开车看海,有人leetcode第一题都做不出来。 希望下面的题解可以帮助你们开始 你们的 leetcode 刷题 的 天降之路 题目 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中…...

PHP 通过 Redis 解决并发请求的操作问题
比如PHP收到两个并发的请求A和B,要求只能其中一个请求处理S1操作,另一个请求直接返回失败,可以通过redis去解决: SETNX(SET if Not eXists)是 Redis 中的一个原子命令,用于设置键-值对…...
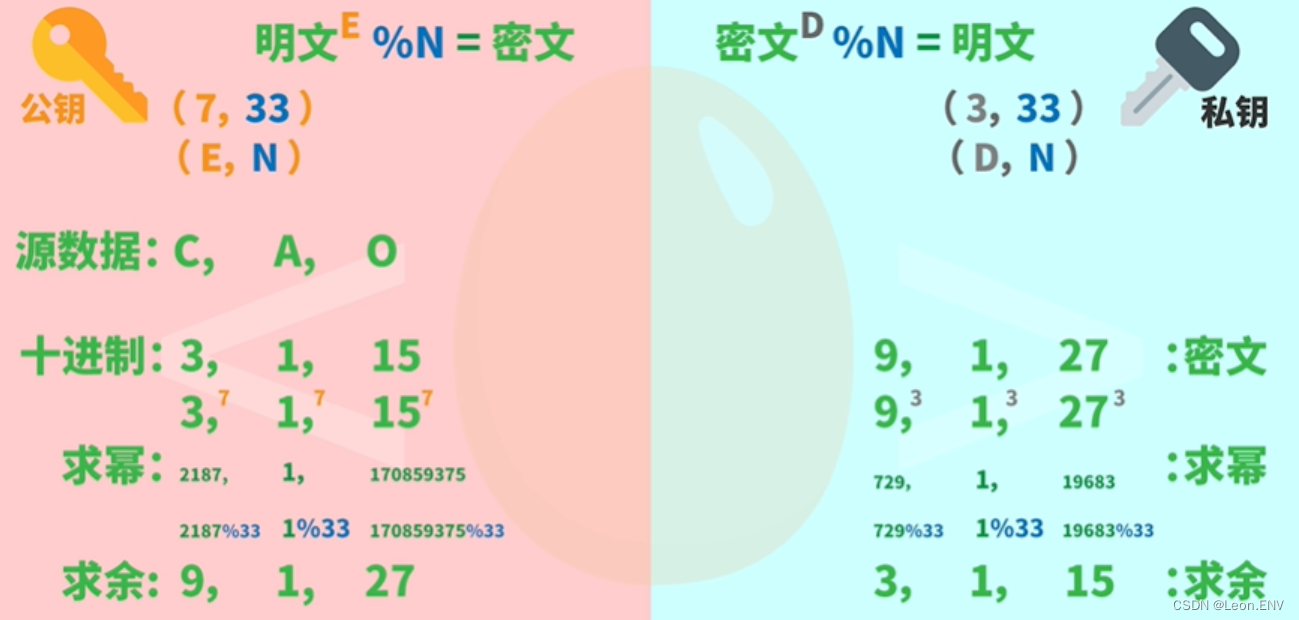
浅谈信息论和信息编码
目录 背景 信息是什么 信息度量 小白鼠实验 哈夫曼编码 密码学 其它应用 背景 克劳德艾尔伍德香农(Claude Elwood Shannon)出生于 1916 年 美国密歇根州。1936 年毕业于密歇根大学,获得数学和电子工程学士学位。之后,他在麻…...

【测试】笔试02
文章目录 1. 下面不属于软件测试步骤的是2. 关于测试驱动开发,描述错误的是3. 在软件测试中,圈复杂度(Cyclomatic complexity):代码逻辑复杂度的度量,提供了被测代码的路径数量。圈复杂度可通过系统控制流图…...

公司内部网段多管控乱,该如何规范跨网文件传输交换?
古往今来,高筑墙一直是有效的防御措施。从边塞长城到护城河外的高高城墙,都是利用隔离地域的形式实现保护安全域的效果。这样一来,城内的安全域可以在遇到危险时受到有效保护。 在企业网络安全防护方面,网络安全域隔离也是网络安全…...

Ceph入门到精通-OSD waring 设置建议
OSD 以下检查表明 OSD 节点存在问题。 警告 1 在 /var/lib/ceph/osd 中找到的多个ceph_fsid值。 这可能意味着您正在托管许多集群的 OSD 此节点或某些 OSD 配置错误以加入 您期望的集群。 2 设置可能会导致数据丢失,因为如果 未达到最小值,Ceph 将不会确…...
软件测试工程师如何快速理解业务?
1. 阅读需求文档和业务资料 仔细阅读与业务相关的文档和资料对于理解业务至关重要。 需求文档通常描述了软件的功能和用户需求,而业务规范则详细说明了业务流程、规则和标准。 仔细阅读这些文档,你可以了解业务的基本概念、要求和流程。 同时&#x…...

【教程】部署apprtc服务中安装google-cloud-cli组件的问题及解决
#0# 前置条件 已经安装完成node,grunt,node 组件和python pip包等。需要安装google-cloud-cli组件。 Ubuntu安装google-cloud-cli组件 apprtc项目运行需要google-cloud-cli前置组件,且运行其中的dev_appserver.py。 根据google官方的关于安…...

C++——shared_ptr:make_shared的用处,与shared_ptr直接构造的区别
shared_ptr shared_ptr继承自__shared_ptr,其中有两个对象,一个是指向资源的指针,一个是控制块,指向一个引用计数对象。控制块中存储了强引用和弱引用的计数,强引用Uses代表shared_ptr对象的引用计数,弱引…...
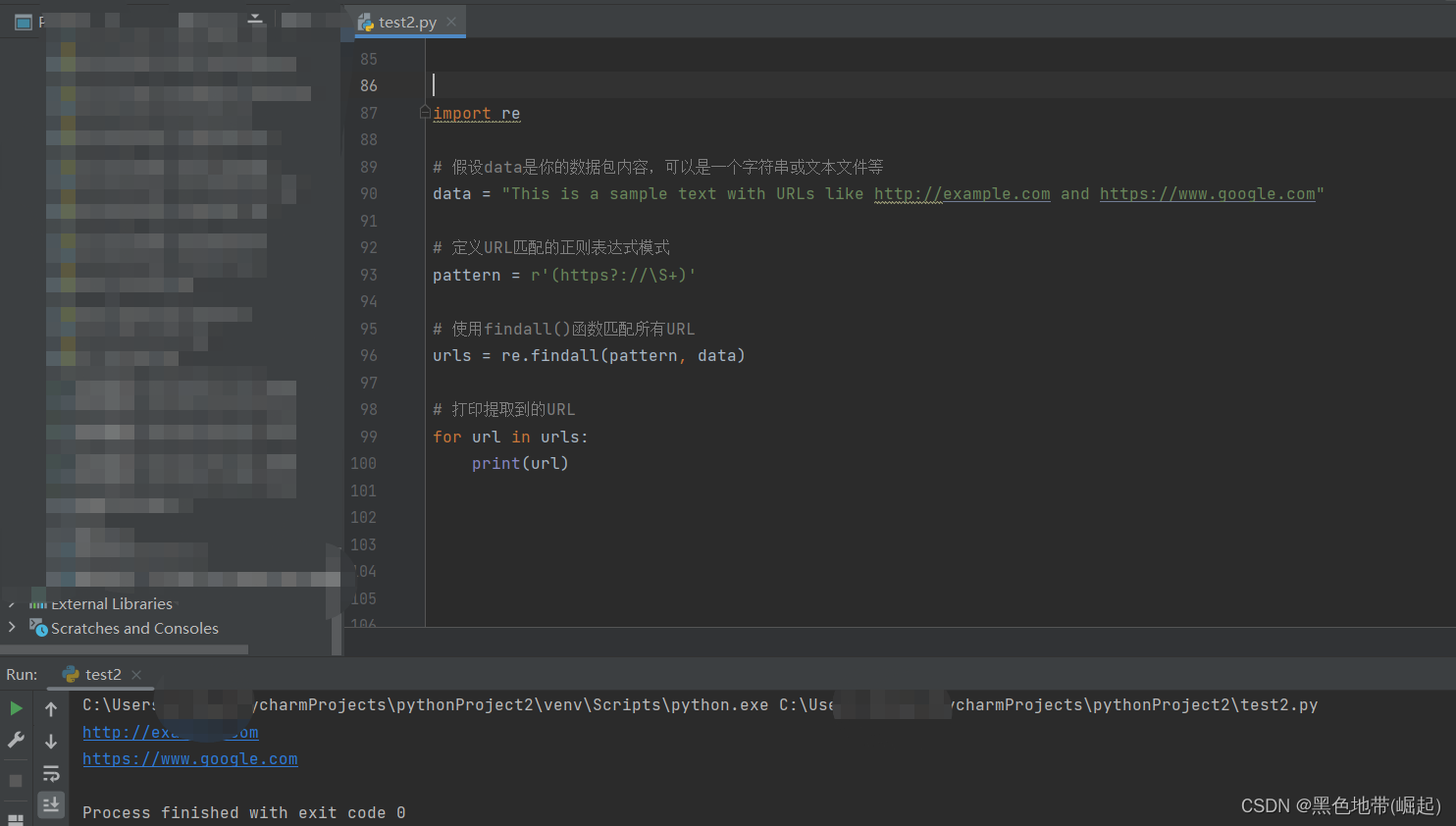
【网络安全带你练爬虫-100练】第17练:分割字符串
目录 一、目标1:使用函数分割 二、目标2:使用函数模块 三、目标3:使用正则匹配 一、目标1:使用函数分割 目标:x.x.x.x[中国北京 xx云] 方法:split函数replace函数 1、分割:使用split()方法将…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
