LA@特征值和特征向量的性质
文章目录
- 方阵特征值和特征向量的性质👺
- 特征值之和
- 特征值之积
- 推论:特征值判定方阵的可逆性
- 证明
- 小结
- 导出性质
- 可逆矩阵的特征值性质
- 转置矩阵和特征值
- 矩阵多项式的特征值
- 不同特征值的特征向量线性无关定理
- 推论
- 推广
- 特征向量线性组合
- 特征值的重数性质
方阵特征值和特征向量的性质👺
特征值之和
- ∑ i = 1 n λ i = ∑ i = 1 n a i i \sum\limits_{i=1}^{n}\lambda_i=\sum\limits_{i=1}^{n}a_{ii} i=1∑nλi=i=1∑naii
- 其中 ∑ i = 1 n a i i \sum_{i=1}^{n}a_{ii} ∑i=1naii称为矩阵的迹,记为 T r ( A ) Tr(\bold A) Tr(A)
特征值之积
- ∏ i = 1 n λ i = ∣ A ∣ \prod_{i=1}^{n}\lambda_{i}=|A| ∏i=1nλi=∣A∣
推论:特征值判定方阵的可逆性
- 方阵 A \bold{A} A可逆的条件是其的特征值不全为0
- 证明:
- 由特征值之积的性质可知,当方阵 A \bold{A} A的特征值之积不为0,意味着 ∣ A ∣ ≠ 0 |\bold{A}|\neq{0} ∣A∣=0从而 A \bold{A} A是可逆的
证明
-
借助多项式的知识来同时证明上述两条性质(同次项系数相等原理)
-
对于
-
f ( λ ) = ∣ λ E − A ∣ = ∣ λ − a 11 − a 12 ⋯ − a 1 n − a 21 λ − a 22 ⋯ − a 2 n ⋮ ⋮ ⋮ − a n 1 − a n 2 ⋯ λ − a n n ∣ f(\lambda)=|\lambda{E}-A|= \begin{vmatrix} \lambda-a_{11}& -a_{12}& \cdots&-a_{1n} \\ -a_{21}& \lambda-a_{22}& \cdots&-a_{2n} \\ \vdots& \vdots& &\vdots \\ -a_{n1}& -a_{n2}& \cdots&\lambda-a_{nn} \\ \end{vmatrix} f(λ)=∣λE−A∣= λ−a11−a21⋮−an1−a12λ−a22⋮−an2⋯⋯⋯−a1n−a2n⋮λ−ann
-
f ( λ ) f(\lambda) f(λ)行列式展开后有 n ! n! n!项(未合并化简同类项前),把它们记为 θ k , k = 1 , 2 , ⋯ , n ! \theta_k,k=1,2,\cdots,n! θk,k=1,2,⋯,n!, θ k = ( − 1 ) τ ( p k ) ∏ i = 1 n a i , j i \theta_k=(-1)^{\tau(p_k)}\prod_{i=1}^{n}a_{i,j_i} θk=(−1)τ(pk)∏i=1nai,ji,其中 p k p_k pk是第 k k k个 n n n级排列 ( j 1 , ⋯ , j n ) (j_1,\cdots,j_n) (j1,⋯,jn)
-
将合并同类相(多项式的一般形式): f ( λ ) f(\lambda) f(λ)= ∑ i = 0 n a i λ i \sum_{i=0}^{n}a_i\lambda^{i} ∑i=0naiλi
<1>-
<1>式中有1项是由主对角线元素相乘的积,是 n n n次项,同时也是最高次项),把它记为- θ d = ( λ − a 11 ) ( λ − a 22 ) ⋯ ( λ − a n n ) \theta_d=(\lambda-a_{11})(\lambda-a_{22})\cdots(\lambda-a_{nn}) θd=(λ−a11)(λ−a22)⋯(λ−ann),这也是一个关于 λ \lambda λ,的 n n n次多项式
-
其余项至多含有对角线元素的 n − 2 n-2 n−2个元素(次高项的次数为 n − 2 n-2 n−2)
- 因为每个项的因子都取自不同行不同列
- 事实上,行列式展开的的 n ! n! n!项求和式中,每一项都包含行列式中的某 n n n个元素的乘积作为因式,如果因式中不包含某个对角线元素(设取自第 i i i行的元素不来自第 i i i列,记为 e 1 e_1 e1),那么必定存在一个元素(设取自第 j j j行,记为 e 2 e_2 e2)是来自第 i i i列的,这就导致第 i , j i,j i,j行取出的元素 e 1 , e 2 e_1,e_2 e1,e2都不是对角线上的元素( i ≠ j i\neq{j} i=j)
-
因此,容易确定
<1>中 a n , a n − 1 a_n,a_{n-1} an,an−1都是由 θ d \theta_{d} θd所确定的 -
现在,我们只对 ξ \xi ξ这一项感兴趣,由多项式相关知识,容易做出以下推导
- θ d \theta_d θd= λ n − ( a 11 + a 22 + ⋯ + a n n ) λ n − 1 + ⋯ \lambda^{n}-(a_{11}+a_{22}+\cdots+a_{nn})\lambda^{n-1}+\cdots λn−(a11+a22+⋯+ann)λn−1+⋯
- f ( λ ) f(\lambda) f(λ)= θ d + ∑ i , i ≠ d n ! θ i \theta_d+\sum\limits_{i,i\neq{d}}^{n!}\theta_i θd+i,i=d∑n!θi
- 展开式中 n , n − 1 n,n-1 n,n−1次项的系数是只由 θ d \theta_d θd提供,其余 θ i , i ≠ p \theta_i,i\neq{p} θi,i=p只能够提供不超过 n − 2 n-2 n−2次项;
- a n = 1 a_n=1 an=1; a n − 1 = − ∑ i = 1 n a i i a_{n-1}=-\sum_{i=1}^{n}a_{ii} an−1=−∑i=1naii;
- 常数项 a 0 a_0 a0可以通过取 λ = 0 \lambda=0 λ=0得到,即 a 0 = f ( 0 ) = ∣ 0 E − A ∣ = ∣ − A ∣ = ( − 1 ) n ∣ A ∣ a_0=f(0)=|\bold{0E-A}|=|-\bold{A}|=(-1)^n|\bold{A}| a0=f(0)=∣0E−A∣=∣−A∣=(−1)n∣A∣
- f ( λ ) = λ n − ( ∑ i = 1 n a i i ) λ n − 1 + ⋯ ∣ − A ∣ λ 0 f(\lambda)=\lambda^{n}-(\sum_{i=1}^{n}a_{ii})\lambda^{n-1}+\cdots|-A|\lambda^{0} f(λ)=λn−(∑i=1naii)λn−1+⋯∣−A∣λ0
<2> - Notes:参考:math@多项式@求和式乘法
-
-
-
另一方面,设 λ 1 , ⋯ , λ n \lambda_1,\cdots,\lambda_n λ1,⋯,λn是 f ( λ ) f(\lambda) f(λ)的 n n n个特征值(根)
-
对于 n n n次多项式 f ( λ ) f(\lambda) f(λ),他有 n n n个复根,由余式定理,可以因式分解写成如下形式
-
f ( λ ) = ( λ − λ 1 ) ( λ − λ 2 ) ⋯ ( λ − λ n ) f(\lambda)=(\lambda-\lambda_1)(\lambda-\lambda_2)\cdots(\lambda-\lambda_n) f(λ)=(λ−λ1)(λ−λ2)⋯(λ−λn)
-
f ( λ ) f(\lambda) f(λ)= ∏ i = 1 n ( λ − λ i ) \prod_{i=1}^{n}(\lambda-\lambda_i) ∏i=1n(λ−λi)= λ n − ( ∑ i = 1 n λ i ) λ n − 1 + ⋯ + ∏ i = 1 n ( − λ i ) \lambda^n-(\sum_{i=1}^{n}\lambda_i)\lambda^{n-1}+\cdots+\prod_{i=1}^{n}(-\lambda_i) λn−(∑i=1nλi)λn−1+⋯+∏i=1n(−λi)
<3>
-
-
小结
- 对比式
<2>,<3>中的- n − 1 n-1 n−1次项的系数 ∑ i = 1 n a i i = ∑ i = 1 n λ i \sum_{i=1}^{n}a_{ii}=\sum_{i=1}^{n}\lambda_{i} ∑i=1naii=∑i=1nλi
- 0 0 0次项系数 ∣ − A ∣ = ∏ i = 1 n ( − λ i ) |-A|=\prod_{i=1}^{n}(-\lambda_i) ∣−A∣=∏i=1n(−λi),即 ( − 1 ) n ∣ A ∣ = ( − 1 ) n ∏ i n ( λ i ) (-1)^n|A|=(-1)^n\prod_{i}^{n}(\lambda_i) (−1)n∣A∣=(−1)n∏in(λi)所以: ∣ A ∣ = ∏ i n λ i |A|=\prod_{i}^{n}\lambda_i ∣A∣=∏inλi
导出性质
-
设 α , A , λ \alpha,\bold{A},\lambda α,A,λ满足 A α = λ α \bold{A}\alpha=\lambda{\alpha} Aα=λα,则:
- ( k A ) ( k α ) = ( k λ ) ( k α ) (k\bold{A})(k\alpha)=(k\lambda){(k\alpha)} (kA)(kα)=(kλ)(kα)
- A m α = λ m α \bold{A}^m\alpha=\lambda^m\alpha Amα=λmα
-
证明:
-
对 A α = λ α \bold{A}\alpha=\lambda{\alpha} Aα=λα同乘以 k k k,
- ( k A ) α = ( k λ ) α (k\bold{A})\alpha=(k\lambda)\alpha (kA)α=(kλ)α,
- A ( k α ) = λ ( k α ) \bold{A}(k\alpha)=\lambda({k\alpha}) A(kα)=λ(kα)
- 再次乘以 k k k: ( k A ) ( k α ) = ( k λ ) ( k α ) (k\bold{A})(k\alpha)=(k\lambda){(k\alpha)} (kA)(kα)=(kλ)(kα)
-
对 A α = λ α \bold{A}\alpha=\lambda\alpha Aα=λα两边同时左乘 A \bold{A} A
- A A α = A λ α = λ A α = λ λ α \bold{A}\bold{A}\alpha=\bold{A}\lambda\alpha=\lambda{\bold{A}\alpha}=\lambda{\lambda{\alpha}} AAα=Aλα=λAα=λλα,所以:
- A 2 α = λ 2 α \bold{A}^2\alpha=\lambda^2\alpha A2α=λ2α;
- 类似的 A 3 α = A λ 2 α , λ 2 A α = λ 3 α \bold{A}^3\alpha=\bold{A}\lambda^2\alpha,\lambda^2\bold{A}\alpha=\lambda^3\alpha A3α=Aλ2α,λ2Aα=λ3α
- 重复 m − 1 m-1 m−1次得到: A m α = λ m α \bold{A}^m\alpha=\lambda^m\alpha Amα=λmα
- A A α = A λ α = λ A α = λ λ α \bold{A}\bold{A}\alpha=\bold{A}\lambda\alpha=\lambda{\bold{A}\alpha}=\lambda{\lambda{\alpha}} AAα=Aλα=λAα=λλα,所以:
-
可逆矩阵的特征值性质
- 当 A \bold{A} A可逆时
- λ − 1 α = A − 1 α \lambda^{-1}\alpha=\bold{A}^{-1}\alpha λ−1α=A−1α
- 对 A α = λ α \bold{A}\alpha=\lambda{\alpha} Aα=λα同时左乘 A − 1 \bold{A}^{-1} A−1
- α = λ A − 1 α \alpha=\lambda \bold{A}^{-1}\alpha α=λA−1α,两边同乘以 λ − 1 \lambda^{-1} λ−1, λ − 1 α = A − 1 α \lambda^{-1}\alpha=\bold{A}^{-1}\alpha λ−1α=A−1α
- ( A ∗ ) α = ∣ A ∣ λ α (\bold{A}^*)\alpha=\frac{|\bold{A}|}{\lambda}\alpha (A∗)α=λ∣A∣α
- 方法1:
- A − 1 = 1 ∣ A ∣ A ∗ \bold{A}^{-1}=\frac{1}{|\bold{A}|}\bold{A}^* A−1=∣A∣1A∗,两边同时乘以 α \alpha α: A − 1 α = 1 ∣ A ∣ A ∗ α \bold{A}^{-1}\alpha=\frac{1}{|\bold{A}|}\bold{A}^{*}\alpha A−1α=∣A∣1A∗α
- λ − 1 α = ( 1 ∣ A ∣ A ∗ ) α \lambda^{-1}\alpha=(\frac{1}{|\bold{A}|}\bold{A}^*)\alpha λ−1α=(∣A∣1A∗)α
- ∣ A ∣ λ α = ( A ∗ ) α \frac{|\bold{A}|}{\lambda}\alpha=(\bold{A}^*)\alpha λ∣A∣α=(A∗)α
- 所以 ( A ∗ ) α = ∣ A ∣ λ α (\bold{A}^*)\alpha=\frac{|\bold{A}|}{\lambda}\alpha (A∗)α=λ∣A∣α
- 方法2:
- A ∗ = ∣ A ∣ A − 1 \bold{A^{*}=|A|A^{-1}} A∗=∣A∣A−1,两边同时乘以 α \alpha α, ( A ∗ ) α = ∣ A ∣ A − 1 α \bold{(A^{*})\alpha=|A|A^{-1}\alpha} (A∗)α=∣A∣A−1α
- ∣ A ∣ A − 1 α = ∣ A ∣ λ − 1 α \bold{|A|A^{-1}\alpha=|A|\lambda^{-1}\alpha} ∣A∣A−1α=∣A∣λ−1α
- 所以 ( A ∗ ) α = ∣ A ∣ λ α (\bold{A}^*)\alpha=\frac{|\bold{A}|}{\lambda}\alpha (A∗)α=λ∣A∣α
- 方法1:
- λ − 1 α = A − 1 α \lambda^{-1}\alpha=\bold{A}^{-1}\alpha λ−1α=A−1α
转置矩阵和特征值
-
方阵 A \bold{A} A的转置 A T \bold{A}^T AT的特征值和 A \bold{A} A的特征值相同
-
A : f ( λ ) = ∣ λ E − A ∣ \bold{A}:f(\lambda)=|\lambda{E}-\bold{A}| A:f(λ)=∣λE−A∣
-
A T : f ( λ ) = ∣ λ E − A T ∣ = ∣ ( λ E ) T − A T ∣ = ∣ ( λ E − A ) T ∣ = ∣ λ E − A ∣ \bold{A}^T:f(\lambda)=|\lambda{E}-\bold{A}^T|=|(\lambda{E})^T-\bold{A}^T|=|(\lambda{E}-\bold{A})^T|=|\lambda{E}-\bold{A}| AT:f(λ)=∣λE−AT∣=∣(λE)T−AT∣=∣(λE−A)T∣=∣λE−A∣
-
可见, A , A T \bold{A},\bold{A}^T A,AT具有相同的特征方程,因此特征值一定相同
-
-
但是它们的特征向量不一定相同
- 因为前面我们讨论过,特征值不能够唯一确定特征向量
矩阵多项式的特征值
-
设 p ( x ) = ∑ i = 0 m a i x i = ∑ i = 0 m a m − i x m − i p(x)=\sum\limits_{i=0}^{m}a_{i}x^i=\sum\limits_{i=0}^{m}a_{m-i}x^{m-i} p(x)=i=0∑maixi=i=0∑mam−ixm−i; λ , A , α \lambda,\bold{A},\alpha λ,A,α满足 A α = λ α \bold{A}\alpha=\lambda\alpha Aα=λα,则 p ( A ) α = p ( λ ) α p(\bold{A})\alpha=p(\lambda)\alpha p(A)α=p(λ)α
-
证明:
-
p ( A ) α = ∑ i = 0 m a i A i α p(\bold{A})\alpha=\sum\limits_{i=0}^{m}a_{i}\bold{A}^i\alpha p(A)α=i=0∑maiAiα= ∑ i = 0 m a i λ i α \sum\limits_{i=0}^{m}a_{i}\lambda^i\alpha i=0∑maiλiα,而 p ( λ ) = ∑ i = 0 m a i λ i p(\lambda)=\sum\limits_{i=0}^{m}a_{i}\lambda^i p(λ)=i=0∑maiλi;从而 p ( λ ) α = ∑ i = 0 m a i λ i α p(\lambda)\alpha=\sum\limits_{i=0}^{m}a_{i}\lambda^i\alpha p(λ)α=i=0∑maiλiα
-
因此 p ( A ) α = p ( λ ) α p(\bold{A})\alpha=p(\lambda)\alpha p(A)α=p(λ)α
-
不同特征值的特征向量线性无关定理
- 设 n n n阶方阵 A \bold{A} A的 n n n个不同特征值为 λ i , i = 1 , 2 , ⋯ , m \lambda_i,i=1,2,\cdots,m λi,i=1,2,⋯,m,( λ i ≠ λ j \lambda_i\neq{\lambda_{j}}\, λi=λjif i ≠ j i\neq{j} i=j); A \bold{A} A关于 λ i \lambda_i λi对应的特征向量分别记为 α i , i = 1 , 2 , ⋯ , m \alpha_i,i=1,2,\cdots,m αi,i=1,2,⋯,m;那么 A 0 : α 1 , ⋯ , α m A_0:\alpha_1,\cdots,\alpha_m A0:α1,⋯,αm线性无关
- 即:方阵的属于不同特征值的特征向量线性无关
- 证明:
-
对特征值的个数 m m m作数学归纳法
-
当 m = 1 m=1 m=1时, α 1 ≠ 0 \bold{\alpha_1\neq{0}} α1=0, A 0 : α 1 A_0:\alpha_1 A0:α1仅含有一个非零向量的向量组线性无关
-
设 m = k − 1 m=k-1 m=k−1时结论成立,即 A k − 1 : α 1 , ⋯ , α k − 1 A_{k-1}:\alpha_1,\cdots,\alpha_{k-1} Ak−1:α1,⋯,αk−1线性无关
-
这里的思路是假设 m = k − 1 m=k-1 m=k−1时结论能推出 m = k m=k m=k时也成立
- (当然也可以设 m = k m=k m=k时成立然后推 m = k + 1 m=k+1 m=k+1时仍然成立)
-
设向量组 A k : α 1 , ⋯ , α k A_{k}:\alpha_1,\cdots,\alpha_k Ak:α1,⋯,αk,其线性相关性判定式 ∑ i = 1 k x i α i = 0 \sum_{i=1}^{k}x_i\alpha_i=\bold{0} ∑i=1kxiαi=0
(1) -
用 A \bold{A} A左乘
(1)式两边,得 ∑ i = 1 k x i A α i = 0 \sum_{i=1}^{k}x_i\bold{A}\alpha_i=\bold{0} ∑i=1kxiAαi=0(2) -
由 A α i = λ α i \bold{A}\alpha_i=\lambda{\alpha_i} Aαi=λαi代入
(2)得 ∑ i = 1 k x i λ i α i = 0 \sum_{i=1}^{k}x_i\lambda_i\alpha_i=\bold{0} ∑i=1kxiλiαi=0(3) -
作 ( 3 ) − λ k ( 2 ) (3)-\lambda_k(2) (3)−λk(2)得: ∑ i = 1 k x i ( λ i − λ k ) α i = 0 \sum_{i=1}^{k}x_i(\lambda_i-\lambda_k)\alpha_i=\bold{0} ∑i=1kxi(λi−λk)αi=0,等式左侧展开式得最后一项为0,化简后即 ∑ i = 1 k − 1 x i ( λ i − λ k ) α i = 0 \sum_{i=1}^{k-1}x_i(\lambda_i-\lambda_k)\alpha_i=\bold{0} ∑i=1k−1xi(λi−λk)αi=0
(4) -
由归纳假设,
(4)中的表出系数 γ i = x i ( λ i − λ k ) = 0 \gamma_i=x_i(\lambda_i-\lambda_k)=0 γi=xi(λi−λk)=0, i = 1 , ⋯ , k − 1 i=1,\cdots,k-1 i=1,⋯,k−1- 由条件中的特征值互异性: λ i ≠ λ j \lambda_i\neq{\lambda_j} λi=λj, i = 1 , ⋯ , m i=1,\cdots,m i=1,⋯,m可知 λ i − λ k ≠ 0 \lambda_i-\lambda_k\neq{0} λi−λk=0, i = 1 , ⋯ , k − 1 i=1,\cdots,k-1 i=1,⋯,k−1
- 从而 γ i = 0 \gamma_i=0 γi=0一定有 x i = 0 x_i=0 xi=0, i = 1 , ⋯ , k − 1 i=1,\cdots,k-1 i=1,⋯,k−1;代入
(1)可知 x k α k = 0 x_k\alpha_k=\bold{0} xkαk=0,而 α k ≠ 0 \alpha_k\neq{\bold{0}} αk=0,所以 x k = 0 x_k=0 xk=0 - 从而
(1)中表出系数 x i = 0 , i = 1 , ⋯ , k x_i=0,i=1,\cdots,k xi=0,i=1,⋯,k,即 A k : α 1 , ⋯ , α k A_k:\alpha_1,\cdots,\alpha_k Ak:α1,⋯,αk线性无关
-
-
由归纳法原理,命题成立
-
Note:这个归纳法证明中,最重要的一个步骤是等式
(4)的构造过程,它将 m = k m=k m=k时的命题和 m = k − 1 m=k-1 m=k−1时的命题(归纳假设条件)联系起来
-
推论
- 设 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2是方阵 A \bold{A} A的两个不同特征值 ( λ 1 ≠ λ 2 ) (\lambda_1\neq{\lambda_2}) (λ1=λ2),且 S 1 : ξ 1 , ⋯ , ξ s S_1:\xi_1,\cdots,\xi_s S1:ξ1,⋯,ξs和 S 2 : η 1 , ⋯ , η t S_2:\eta_1,\cdots,\eta_t S2:η1,⋯,ηt分别是对应于 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2的线性无关特征向量组,则 S 1 , S 2 S_1,S_2 S1,S2合并的向量组 S 3 S_3 S3线性无关
推广
-
记特征值 λ i \lambda_i λi, i = 1 , ⋯ , m i=1,\cdots,m i=1,⋯,m的线性无关特征向量组为 A i : α i 1 , α i 2 , ⋯ , α i s i A_i:\alpha_{i1},\alpha_{i2},\cdots,\alpha_{is_i} Ai:αi1,αi2,⋯,αisi😭 A i A_i Ai相当于方程 ( λ i E − A ) x = 0 (\lambda_iE-\bold{A})x=0 (λiE−A)x=0的一个基础解系),则这些向量组的合并向量组 B : A 1 , ⋯ , A n B:A_1,\cdots,A_n B:A1,⋯,An依然线性无关
-
也即是说,属于各个特征值的线性无关特征向量合在一起构成的向量组依然线性无关
-
证明:
-
对特征值个数 m m m作数学归纳法,过程和本节定理得证明过程类似
-
当 m = 1 m=1 m=1时,结论显然成立 S 3 = S 1 S_3=S_1 S3=S1是线性无关的
-
设 m = k m=k m=k时结论成立,
-
当 m = k + 1 m=k+1 m=k+1时,设 ∑ i = 1 k + 1 ∑ j = 1 s i x i j α i j = 0 \sum_{i=1}^{k+1}\sum_{j=1}^{s_i}x_{ij}\alpha_{ij}=\bold{0} ∑i=1k+1∑j=1sixijαij=0
<1>-
对
<1>两边同时左乘 A \bold{A} A: ∑ i = 1 k + 1 ∑ j = 1 s i x i j A α i j = 0 \sum_{i=1}^{k+1}\sum_{j=1}^{s_i}x_{ij}\bold{A}\alpha_{ij}=\bold{0} ∑i=1k+1∑j=1sixijAαij=0<2> -
将 A λ i = λ i α i j \bold{A}\lambda_i=\lambda_i\alpha_{ij} Aλi=λiαij, i = 1 , ⋯ , s i i=1,\cdots,s_i i=1,⋯,si,代入
<2>得: ∑ i = 1 k + 1 ∑ j = 1 s i x i j λ i α i j = 0 \sum_{i=1}^{k+1}\sum_{j=1}^{s_i}x_{ij}\lambda_{i}\alpha_{ij}=\bold{0} ∑i=1k+1∑j=1sixijλiαij=0<3>- 展开
<3.1>
∑ i = 1 k + 1 ∑ j = 1 s i x i j λ i α i j = ∑ i = 1 k ∑ j = 1 s i x i j λ i α i j + ∑ j = 1 s k + 1 x k + 1 , j λ k + 1 α k + 1 , j = 0 \sum_{i=1}^{k+1}\sum_{j=1}^{s_i}x_{ij}\lambda_{i}\alpha_{ij} =\sum_{i=1}^{k}\sum_{j=1}^{s_i}x_{ij}\lambda_{i}\alpha_{ij} +\sum_{j=1}^{s_{k+1}}x_{k+1,j}\lambda_{k+1}\alpha_{k+1,j} =\bold{0} i=1∑k+1j=1∑sixijλiαij=i=1∑kj=1∑sixijλiαij+j=1∑sk+1xk+1,jλk+1αk+1,j=0
- 展开
-
对
<1>两边同时乘以 λ k + 1 \lambda_{k+1} λk+1得: ∑ i = 1 k + 1 ∑ j = 1 s i x i j λ k + 1 α i j = 0 \sum_{i=1}^{k+1}\sum_{j=1}^{s_i}x_{ij}\lambda_{k+1}\alpha_{ij}=\bold{0} ∑i=1k+1∑j=1sixijλk+1αij=0<4>-
展开
<4.1> -
∑ i = 1 k + 1 ∑ j = 1 s i x i j λ k + 1 α i j = ∑ i = 1 k ∑ j = 1 s i x i j λ k + 1 α i j + ∑ j = 1 s k + 1 x k + 1 , j λ k + 1 α k + 1 , j = 0 \sum_{i=1}^{k+1}\sum_{j=1}^{s_i}x_{ij}\lambda_{k+1}\alpha_{ij} =\sum_{i=1}^{k}\sum_{j=1}^{s_i}x_{ij}\lambda_{k+1}\alpha_{ij} +\sum_{j=1}^{s_{k+1}}x_{k+1,j}\lambda_{k+1}\alpha_{k+1,j} =\bold{0} i=1∑k+1j=1∑sixijλk+1αij=i=1∑kj=1∑sixijλk+1αij+j=1∑sk+1xk+1,jλk+1αk+1,j=0
-
-
作
<3>-<4>,即<3.1>-<4.1>得- ∑ i = 1 k + 1 ∑ j = 1 s i x i j ( λ i − λ k + 1 ) α i j = ∑ i = 1 k ∑ j = 1 s i x i j ( λ i − λ k + 1 ) α i j = 0 \sum_{i=1}^{k+1}\sum_{j=1}^{s_i}x_{ij} (\lambda_i-\lambda_{k+1})\alpha_{ij} =\sum_{i=1}^{k}\sum_{j=1}^{s_i}x_{ij} (\lambda_i-\lambda_{k+1})\alpha_{ij} =\bold{0} i=1∑k+1j=1∑sixij(λi−λk+1)αij=i=1∑kj=1∑sixij(λi−λk+1)αij=0
-
<3>左边展开式中 i = k + 1 i=k+1 i=k+1的被化简
-
-
由归纳假设, ∑ i = 1 k ∑ j = 1 s i γ i j α i j = 0 \sum_{i=1}^{k}\sum_{j=1}^{s_i} \gamma_{ij}\alpha_{ij} =\bold{0} ∑i=1k∑j=1siγijαij=0其中 γ i j = 0 \gamma_{ij}=0 γij=0,所以, γ i j = x i j ( λ i − λ k + 1 ) = 0 \gamma_{ij}=x_{ij}(\lambda_i-\lambda_{k+1})=0 γij=xij(λi−λk+1)=0, i = 1 , ⋯ , k i=1,\cdots,k i=1,⋯,k, j = 1 , ⋯ , s i j=1,\cdots,s_{i} j=1,⋯,si
-
由 λ i , i = 1 , ⋯ , m \lambda_i,i=1,\cdots,m λi,i=1,⋯,m的互异性可知, λ i − λ k + 1 ≠ 0 \lambda_i-\lambda_{k+1}\neq{0} λi−λk+1=0,所以 x i j = 0 x_{ij}=0 xij=0
-
代入
<1>得 ∑ j = 1 s k + 1 x k + 1 , j α k + 1 , j = 0 \sum_{j=1}^{s_{k+1}}x_{k+1,j}\alpha_{k+1,j}=\bold{0} ∑j=1sk+1xk+1,jαk+1,j=0- 由 A k + 1 : α k + 1 , 1 , ⋯ , α k + 1 , s k + 1 A_{k+1}:\alpha_{k+1,1},\cdots,\alpha_{k+1,s_{k+1}} Ak+1:αk+1,1,⋯,αk+1,sk+1线性无关可知, x k + 1 , j = 0 x_{k+1,j}=0 xk+1,j=0, j = 1 , ⋯ , s k + 1 j=1,\cdots,s_{k+1} j=1,⋯,sk+1
- 所以 x 1 , 1 , ⋯ , x k + 1 , s k + 1 x_{1,1},\cdots,x_{k+1,s_{k+1}} x1,1,⋯,xk+1,sk+1全为0,即 B : A 1 , ⋯ , A k + 1 B:A_1,\cdots,A_{k+1} B:A1,⋯,Ak+1线性无关
-
-
由归纳法原理,结论成立
-
特征向量线性组合
同一矩阵的同一特征值的特征向量线性组合仍然是矩阵的特征向量
-
设 α \alpha α是矩阵 A \bold A A属于特征值 λ 0 \lambda_0 λ0的特征向量(用符号语言可以简介的表示为:
- α , A → λ \alpha,{A}\to{\lambda} α,A→λ
- 或者更直接的 A α = λ 0 α A\alpha=\lambda_0\alpha Aα=λ0α
-
设 α 1 , α 2 , A , λ 0 \alpha_1,\alpha_2,\bold A,\lambda_0 α1,α2,A,λ0满足 A α 1 = λ 0 α 1 \bold{A\alpha_1=\lambda_{0}\alpha_1} Aα1=λ0α1; A α 2 = λ 0 α 2 \bold{A\alpha_2=\lambda_0\alpha_2} Aα2=λ0α2,则:
- β = k α 1 \beta=k\alpha_1 β=kα1满足 A β = λ 0 β A\beta=\lambda_0\beta Aβ=λ0β
- 因为 A ( k α 1 ) = k A α 1 \bold{A}(k\alpha_1)=k\bold{A}\alpha_1 A(kα1)=kAα1= k λ 0 α 1 = λ 0 ( k α 1 ) k\lambda_0{\alpha_1}=\lambda_{0}(k\alpha_1) kλ0α1=λ0(kα1)
- γ = α 1 + α 2 \gamma=\alpha_1+\alpha_2 γ=α1+α2满足 A γ = λ 0 γ A\gamma=\lambda_0\gamma Aγ=λ0γ
- A ( α 1 + α 2 ) \bold{A(\alpha_1+\alpha_2)} A(α1+α2)= A α 1 + A α 2 \bold{A\alpha_1+A\alpha_2} Aα1+Aα2= λ 0 α 1 + λ 0 α 2 = λ 0 ( α 1 + α 2 ) \lambda_0\alpha_1+\lambda_0\alpha_2=\lambda_0(\alpha_1+\alpha_2) λ0α1+λ0α2=λ0(α1+α2)
- 综合上述结论,可以得出:若 α i \alpha_i αi, A , λ 0 \bold{A},\lambda_0 A,λ0满足 A α i = α i λ 0 A\alpha_i=\alpha_i\lambda_0 Aαi=αiλ0, ( i = 1 , 2 , ⋯ , n ) (i=1,2,\cdots,n) (i=1,2,⋯,n)则 α i \alpha_i αi的任意线性组合 θ = ∑ i k i α i \theta=\sum_i{k_i\alpha_i} θ=∑ikiαi满足 A θ = θ λ 0 A\theta=\theta\lambda_0 Aθ=θλ0
- β = k α 1 \beta=k\alpha_1 β=kα1满足 A β = λ 0 β A\beta=\lambda_0\beta Aβ=λ0β
方阵 A \bold{A} A得不同特征值得特征向量之和不是 A \bold{A} A的特征向量
-
使用反证法来证明
-
设 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2是 A \bold{A} A的两个不同特征值,即 A p i = λ i p i \bold{A}\bold{p}_i=\lambda_{i}\bold{p}_i Api=λipi, i = 1 , 2 i=1,2 i=1,2
-
易知 A ( p 1 + p 2 ) = λ 1 p 1 + λ 2 p 2 \bold{A(p_1+p_2)}=\lambda_1{\bold{p}_1}+\lambda_2{\bold{p_2}} A(p1+p2)=λ1p1+λ2p2
-
设 p 3 = p 1 + p 2 \bold{p_3=p_1+p_2} p3=p1+p2是 A \bold{A} A的特征向量,则应存在 λ \lambda λ使得 A p 3 = λ p 3 \bold{Ap_3=\lambda{p_3}} Ap3=λp3,即 λ 1 p 1 + λ 2 p 2 = λ p 3 \lambda_1{\bold{p}_1}+\lambda_2{\bold{p_2}}=\lambda{\bold{p_3}} λ1p1+λ2p2=λp3
-
即 ( λ 1 − λ ) p 1 + ( λ 2 − λ ) p 2 = 0 (\lambda_1-\lambda)\bold{p}_1+(\lambda_2-\lambda)\bold{p_2}=\bold{0} (λ1−λ)p1+(λ2−λ)p2=0
-
由于 p 1 , p 2 \bold{p_1,p_2} p1,p2线性无关,所以 λ i − λ = 0 , i = 1 , 2 \lambda_i-\lambda=0,i=1,2 λi−λ=0,i=1,2,所以 λ 1 = λ 2 = λ \lambda_1=\lambda_2=\lambda λ1=λ2=λ,这与 λ 1 ≠ λ 2 \lambda_1\neq{\lambda_2} λ1=λ2矛盾,所以不存在这样的 λ \lambda λ
-
所以 p 1 + p 2 \bold{p_1+p_2} p1+p2不是 A \bold{A} A的特征向量
-
特征值的重数性质
-
设方阵 A \bold{A} A的特征值 λ 1 , ⋯ , λ m \lambda_{1},\cdots,\lambda_{m} λ1,⋯,λm对,若 λ i \lambda_i λi是一个 k i k_i ki重特征值,那么对应于 λ i \lambda_i λi线性无关特征向量的个数 u i ⩽ k i u_i\leqslant{k_i} ui⩽ki
- 其中 ∑ k i = n \sum{k_i}=n ∑ki=n
-
推论:记 u ( A ) = ∑ u i u(\bold{A})=\sum{u_i} u(A)=∑ui,一个 n n n阶方阵 A \bold{A} A的线性无关特征向量的个数 u ( A ) ⩽ n u(\bold{A})\leqslant{n} u(A)⩽n
相关文章:

LA@特征值和特征向量的性质
文章目录 方阵特征值和特征向量的性质👺特征值之和特征值之积推论:特征值判定方阵的可逆性 证明小结 导出性质可逆矩阵的特征值性质转置矩阵和特征值矩阵多项式的特征值不同特征值的特征向量线性无关定理推论推广 特征向量线性组合特征值的重数性质 方阵特征值和特征…...

Springboot使用kafka事务-生产者方
前言 在上一篇文章中,我们使用了springboot的AOP功能实现了kafka的分布式事务,但是那样实现的kafka事务是不完美的,因为请求进来之后分配的是不同线程,但不同线程使用的kafka事务却是同一个,这样会造成多请求情况下的…...

您的计算机已被.halo勒索病毒感染?恢复您的数据的方法在这里!
导言: 在当今数字时代,网络安全已经成为了我们生活和工作中不可或缺的一部分。然而, .Halo 勒索病毒的出现,使网络威胁变得更加真切和具体。本文91数据恢复将深入介绍 .Halo 勒索病毒的危害,详细探讨如何高效地恢复被其…...

生成式AI颠覆传统数据库的十种方式
对于生成式AI的所有闪光点,这个新时代最大的转变可能深埋在软件堆栈中。AI算法正在不易觉察地改变一个又一个数据库。他们正在用复杂、自适应且看似更直观的AI新功能颠覆传统数据库。 与此同时,数据库制造商正在改变我们存储信息的方式,以便…...
el-date-picker自定义只能选中当前月份和半年内月份等
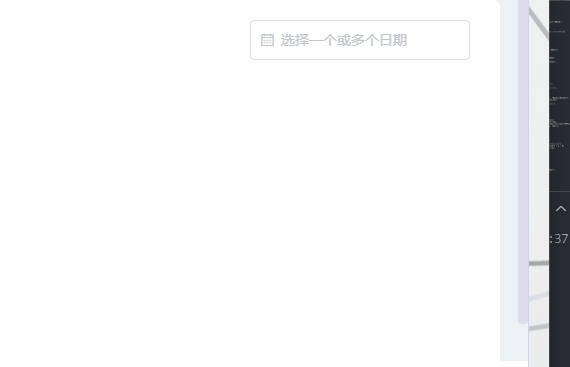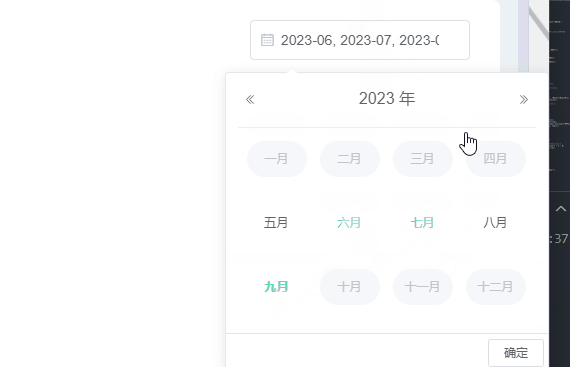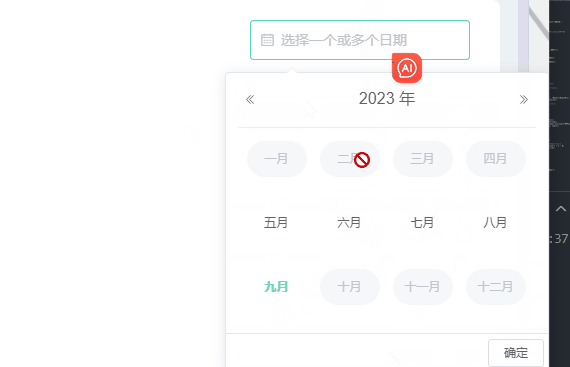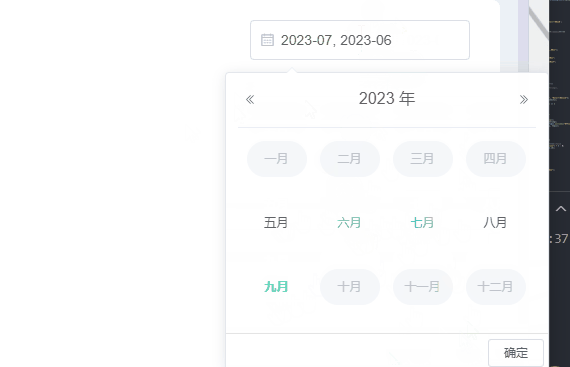
需求:el-date-picker只能选中当前月期和当前月期往前半年,其他时间就禁用了不让选择了,因为没数据哈哈。当然也可以选择往前一年等。 一、效果 二、写个日期选择器 :picker-options:日期选项 value-format:选择后的格…...
:使用Pyecharts绘制带有滑动数据缩放功能的K线图)
Pyecharts教程(十一):使用Pyecharts绘制带有滑动数据缩放功能的K线图
Pyecharts教程(十一):使用Pyecharts绘制带有滑动数据缩放功能的K线图 作者:安静到无声 个人主页 目录 Pyecharts教程(十一):使用Pyecharts绘制带有滑动数据缩放功能的K线图前言步骤总结推荐专栏前言 K线图是金融市场分析中常见的图表类型之一,它能够直观地展示价格的变化…...

2023年高教社杯数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...

POJ 3273 Monthly Expense 二分
我们对每个月花费的最小花费进行二分,对于每一次二分的值mid,计算能花的月份数量,如果月份数量小于等于m,我们就不断的缩小mid,直到找到月份数量小于等于m 与 月份数量大于m的临界值,取最后一次满足条件的m…...
图论(基础)
知识: 顶点,边 | 权,度数 1.图的种类: 有向图 | 无向图 有环 | 无环 联通性 基础1:图的存储(主要是邻接矩阵和邻接表) 例一:B3643 图的存储 - 洛谷 | 计算机科学教育新生态 (…...

docker的运行原理
Docker 是一个开源的容器化技术,它能够让开发者将应用及其依赖打包到一个轻量级的、可移植的容器中,这个容器可以在几乎任何机器上一致地运行。要了解 Docker 的运行原理,我们首先要理解以下几个核心概念: 容器 (Container): 容器是一个轻量级的、独立的、可执行的软件包,…...
vue自定义键盘
<template><div class"mark" click"isOver"></div><div class"mycar"><div class"mycar_list"><div class"mycar_list_con"><p class"mycar_list_p">车牌号</p>…...
k8s 安装 kubernetes安装教程 虚拟机安装k8s centos7安装k8s kuberadmin安装k8s k8s工具安装 k8s安装前配置参数
k8s采用master, node1, node2 。三台虚拟机安装的一主两从,机器已提前安装好docker。下面是机器配置,k8s安装过程,以及出现的问题与解决方法 虚拟机全部采用静态ip, master 30机器, node1 31机器, node2 32机器 机器ip 192.168.164.30 # ma…...

2023年高教社杯数学建模思路 - 案例:感知机原理剖析及实现
文章目录 1 感知机的直观理解2 感知机的数学角度3 代码实现 4 建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 感知机的直观理解 感知机应该属于机器学习算法中最简单的一种算法,其…...
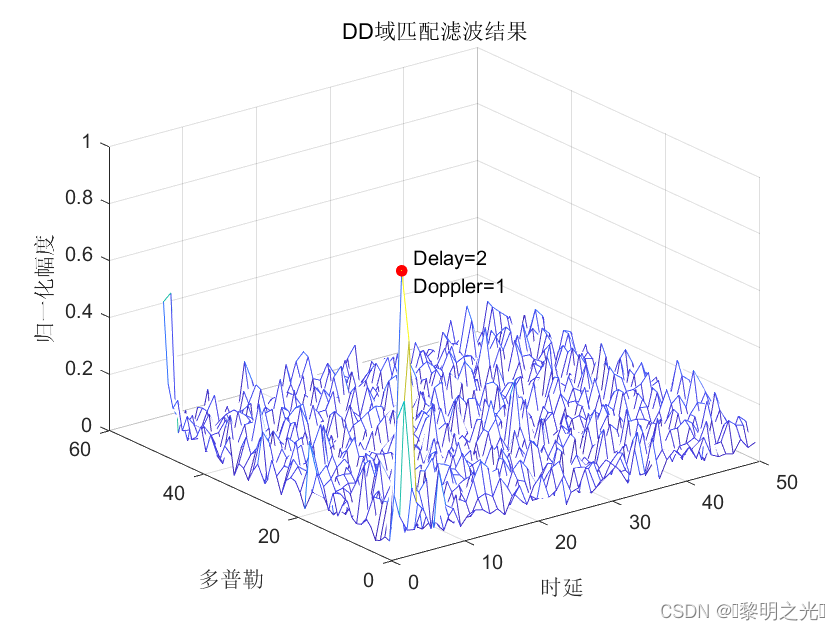
OTFS-ISAC雷达部分最新进展(含matlab仿真+USRP验证)
OTFS基带参数设置 我将使用带宽为80MHz的OTFS波形进行设计,对应参数如下: matlab Tx仿真 Tx导频Tx功率密度谱 帧结构我使用的是经典嵌入导频帧结构,Tx信号波形的带宽从右图可以看出约为80Mhz USRP验证 测试环境 无人机位于1m处 Rx导频Rx…...
Cell | 超深度宏基因组!复原消失的肠道微生物
期刊:Cell IF:64.5 (Q1) 发表时间:2023.6 研究背景 不同的生活方式会影响微生物组组成,但目前微生物组的研究严重偏向于西方工业化人群,其中工业化人群的特点是微生物群多样性较低。为了理解工…...

Centos7 设置代理方法
针对上面变量的设置方法: 1、在/etc/profile文件 2、在~/.bashrc 3、在~/.zshrc 4、在/etc/profile.d/文件夹下新建一个文件xxx.sh 写入如下配置: export proxy"http://192.168.5.14:8118" export http_proxy$proxy export https_proxy$pro…...
)
Android versions (Android 版本)
Android versions (Android 版本) All Android releases https://developer.android.com/about/versions Android 1.0 G1 Android 1.5 Cupcake Android 1.6 Donut Android 2.0 Eclair Android 2.2 Froyo Android 2.3 Gingerbread Android 3.0 Honeycomb Android 4.0 Ic…...
LNMP 平台搭建(四十)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 搭建LNMP 一、安装Nginx 二、安装Mysql 三、安装PHP 四、部署应用 前言 LNMP平台指的是将Linux、Nginx、MySQL和PHP(或者其他的编程语言,如…...

pcie 6.0/7.0相对pcie 5.0的变化有哪些?
引言 话说,小编在CSDN博客跟客服机器人聊天,突然看到有个搜索热搜“pcie最全科普贴”。小编有点似曾相识呀,我就好奇点击了一下,没想到几年前写的帖子在CSDN又火了一把。 说到这里,顺带给自己打个广告哈~ …...

百度Apollo:自动驾驶技术的未来应用之路
文章目录 前言一、城市交通二、出行体验三、环境保护四、未来前景总结 前言 随着科技的不断进步,自动驾驶技术正逐渐成为现实,颠覆着我们的出行方式。作为中国领先的自动驾驶平台,百度Apollo以其卓越的技术和开放的合作精神,正在…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
