PyTorch学习笔记:nn.L1Loss——L1损失
PyTorch学习笔记:nn.L1Loss——L1损失
torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')
功能:创建一个绝对值误差损失函数,即L1损失:
l(x,y)=L={l1,…,lN}T,ln=∣xn−yn∣l(x,y)=L=\{l_1,\dots,l_N\}^T,l_n=|x_n-y_n| l(x,y)=L={l1,…,lN}T,ln=∣xn−yn∣
其中,NNN表示batch size。
函数图像:

输入:
size_average与reduce已经被弃用,具体功能可由reduction替代reduction:指定损失输出的形式,有三种选择:none|mean|sum。none:损失不做任何处理,直接输出一个数组;mean:将得到的损失求平均值再输出,会输出一个数;sum:将得到的损失求和再输出,会输出一个数
注意:
- 输入的xxx与yyy可以是任意维数的数组,但是二者形状必须一致
代码案例
对比reduction不同时,输出损失的差异
import torch.nn as nn
import torchx = torch.rand(10, dtype=torch.float)
y = torch.rand(10, dtype=torch.float)
L1_none = nn.L1Loss(reduction='none')
L1_mean = nn.L1Loss(reduction='mean')
L1_sum = nn.L1Loss(reduction='sum')
out_none = L1_none(x, y)
out_mean = L1_mean(x, y)
out_sum = L1_sum(x, y)
print(x)
print(y)
print(out_none)
print(out_mean)
print(out_sum)
输出
# 用于输入的x
tensor([0.8597, 0.0679, 0.6531, 0.5442, 0.9690, 0.1412, 0.1161, 0.6927, 0.2017, 0.3142])
# 用于输入的y
tensor([0.2538, 0.2823, 0.7768, 0.6710, 0.4303, 0.7249, 0.5897, 0.0048, 0.4121, 0.8169])
# 当reduction设置为none时,输出一个数组
# 该数组上的元素为x,y对应每个元素的绝对值损失,即对应元素做差求绝对值
tensor([0.6059, 0.2143, 0.1237, 0.1268, 0.5387, 0.5837, 0.4737, 0.6879, 0.2103, 0.5027])
# 当reduction设置为mean时,输出所有损失的平均值
tensor(0.4068)
# 当reduction设置为sum时,输出所有损失的和
tensor(4.0677)
注:绘图程序
import torch.nn as nn
import torch
import numpy as np
import matplotlib.pyplot as pltloss = nn.L1Loss(reduction='none')
x = torch.tensor([0]*100)
y = torch.from_numpy(np.linspace(-3,3,100))
loss_value = loss(x,y)
plt.plot(y, loss_value)
plt.savefig('L1Loss.jpg')
官方文档
nn.L1Loss:https://pytorch.org/docs/stable/generated/torch.nn.L1Loss.html#torch.nn.L1Loss
初步完稿于:2022年1月29日
相关文章:

PyTorch学习笔记:nn.L1Loss——L1损失
PyTorch学习笔记:nn.L1Loss——L1损失 torch.nn.L1Loss(size_averageNone, reduceNone, reductionmean)功能:创建一个绝对值误差损失函数,即L1损失: l(x,y)L{l1,…,lN}T,ln∣xn−yn∣l(x,y)L\{l_1,\dots,l_N\}^T,l_n|x_n-y_n| l(…...
Java程序设计-ssm企业财务管理系统设计与实现
摘要系统设计系统实现开发环境:摘要 对于企业集来说,财务管理的地位很重要。随着计算机和网络在企业中的广泛应用,企业发展速度在不断加快,在这种市场竞争冲击下企业财务管理系统必须优先发展,这样才能保证在竞争中处于优势地位。…...

疑难杂症篇(二十一)--Ubuntu18.04安装usb-cam过程出现的问题
对Ubuntu18.04{\rm Ubuntu 18.04}Ubuntu18.04环境下的ROS{\rm ROS}ROS的melodic{\rm melodic}melodic版本安装usb−cam{\rm usb-cam}usb−cam过程出现的两个常见问题提出解决方案。 1.问题1:usb-cam功能包编译时出现"未定义的引用"的问题 问题描述&#…...

npm-npm i XX --save 和--save-dev
之前使用npm i XX --save 和--save-dev 没太在意,就想记录一下,查到一篇比较全的(链接:NPM install -save 和 -save-dev 傻傻分不清),直接看好了,哈哈~ # 安装模块到项目目录下 npm install moduleName # -g 的意思是…...
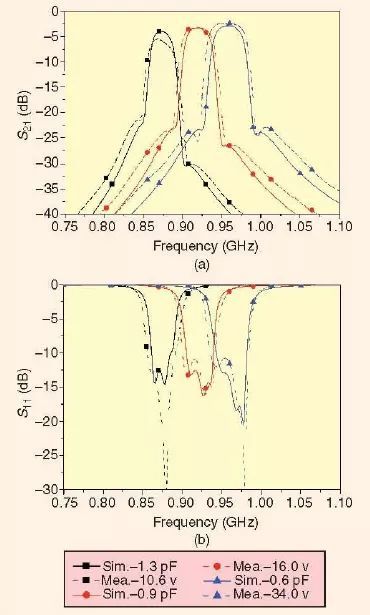
可重构或可调谐微波滤波器技术
电子可重构,或者说电调微波滤波器由于其在改善现在及未来微波系统容量中不断提高的重要性而正吸引着人们越来越多的关注来对其进行研究和开发。例如,崭露头脚的超宽带(UWB)技术要求使用很宽的无线电频谱。然而,作为资源…...
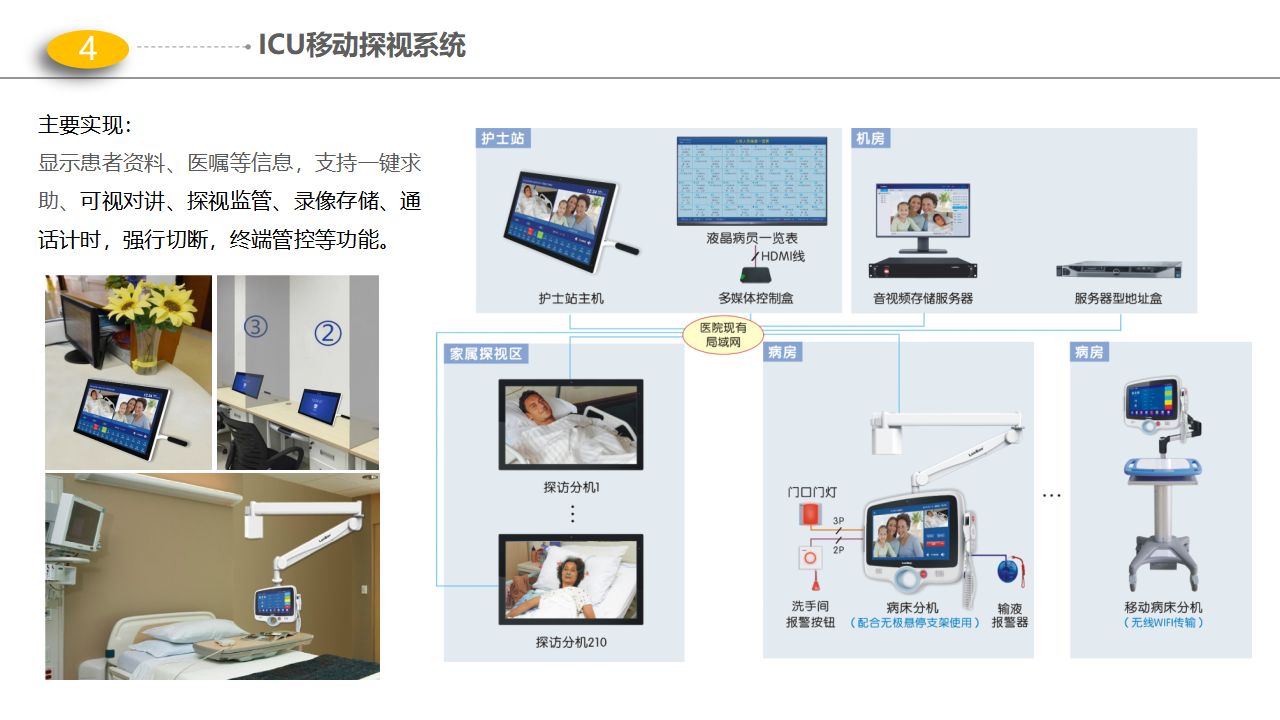
医院智能化解决方案-门(急)诊、医技、智能化项目解决方案
【版权声明】本资料来源网络,知识分享,仅供个人学习,请勿商用。【侵删致歉】如有侵权请联系小编,将在收到信息后第一时间删除!完整资料领取见文末,部分资料内容:篇幅有限,无法完全展…...

判断元素是否在可视区域
前言 在日常开发中,我们经常需要判断目标元素是否在视窗之内或者和视窗的距离小于一个值(例如 100 px),从而实现一些常用的功能,例如: 图片的懒加载列表的无限滚动计算广告元素的曝光情况可点击链接的预加…...

告别传统繁杂的采购合同管理 打造企业自动化采购管理模式
随着企业竞争日趋激烈,采购成本压力剧增,企业对于采购合同管理更加严格,从而把控物资成本。对于任何一家企业采购来说,规范化合同的全面管理,是采购活动中重要的一个环节。 但在如今,依旧有很多企业采购合…...
【prism】路由事件映射到Command命令
在之前的一篇文章中,我介绍了普通的自定义事件: 【wpf】自定义事件总结(Action, EventHandler)_code bean的博客-CSDN博客_wpf action可以说通过Action和EventHandle,自定义事件是相当的方便简单了。https…...
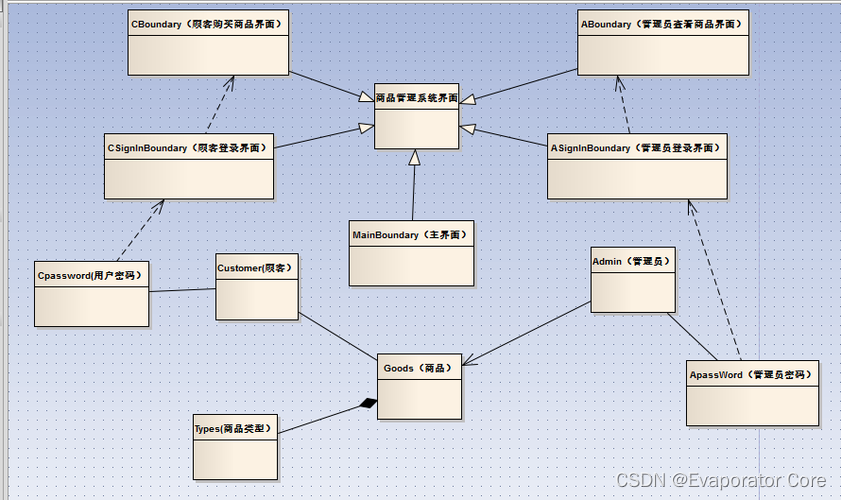
面向对象的基本概念和方法
面向对象的开发方法在近几十年见得以广泛应用,我们常见的Java语言就是一种典型的面向对象的开发语言。然而,面向对象的概念较为复杂,知识点也很细碎,本文整理了面向对象的基本概念和方法,供大家参考。为了便于读者理解…...
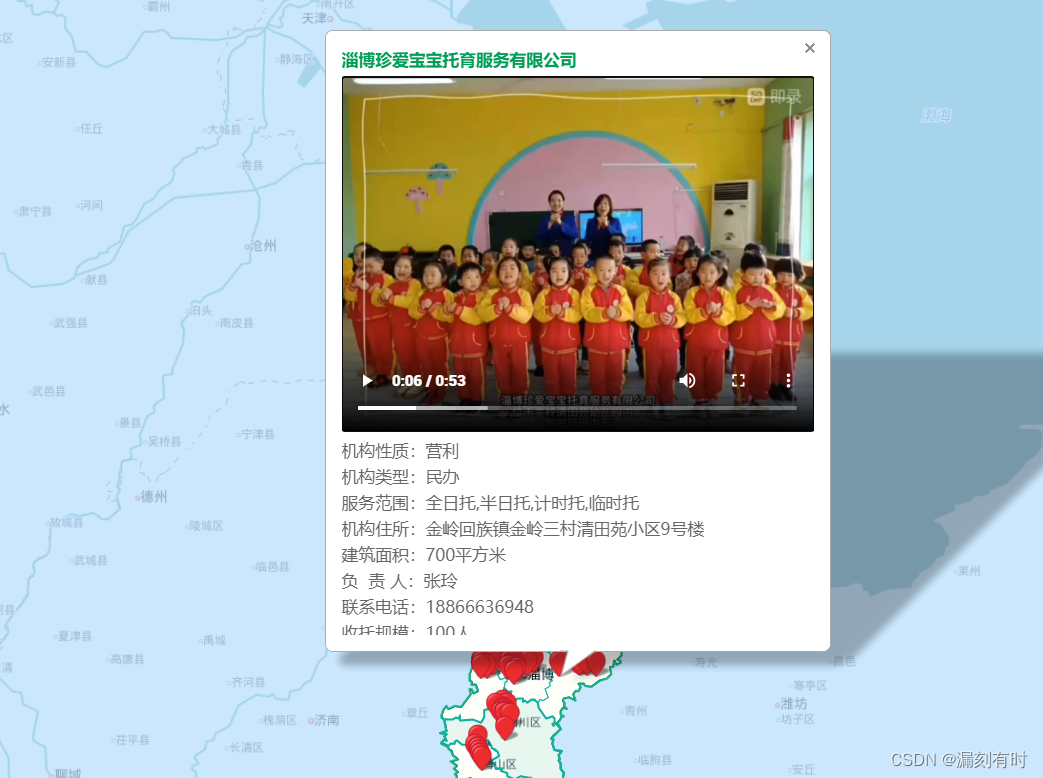
数据可视化大屏百度地图绘制行政区域标注实战案例解析(个性化地图、标注、视频、控件、定位、检索)
百度地图开发系列目录 数据可视化大屏应急管理综合指挥调度系统完整案例详解(PHP-API、Echarts、百度地图)数据可视化大屏百度地图API开发:停车场分布标注和检索静态版百度地图高级开发:map.getDistance计算多点之间的距离并输入…...

1.面向对象和类的关系?2.什么是Promise、3.Promise和async、await的关系
面向对象:面向对象是一种编程思想(oop)。(Js里面所有的东西都可以看做对象,Js它是基于原型的面向对象语言,采用原型的方式来构造对象)很多个具有相同属性和行为的对象就可以抽象为类,对象是类的一个实例。JavaScript在…...
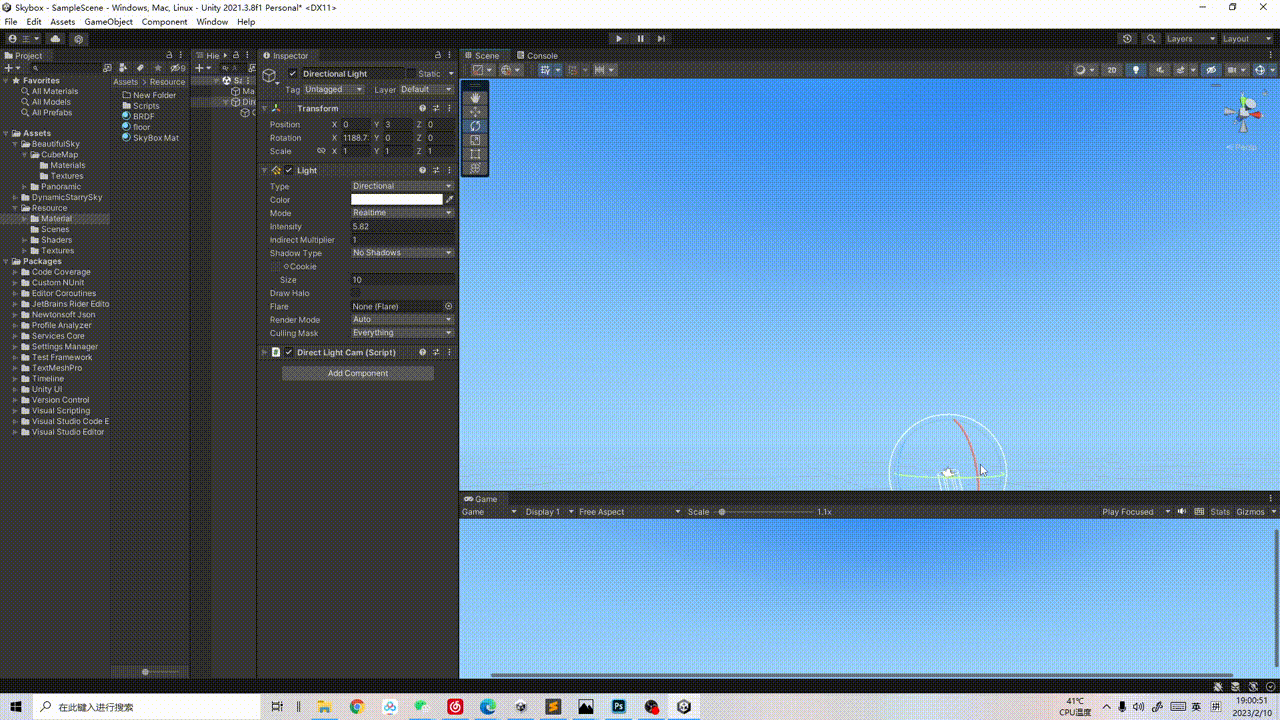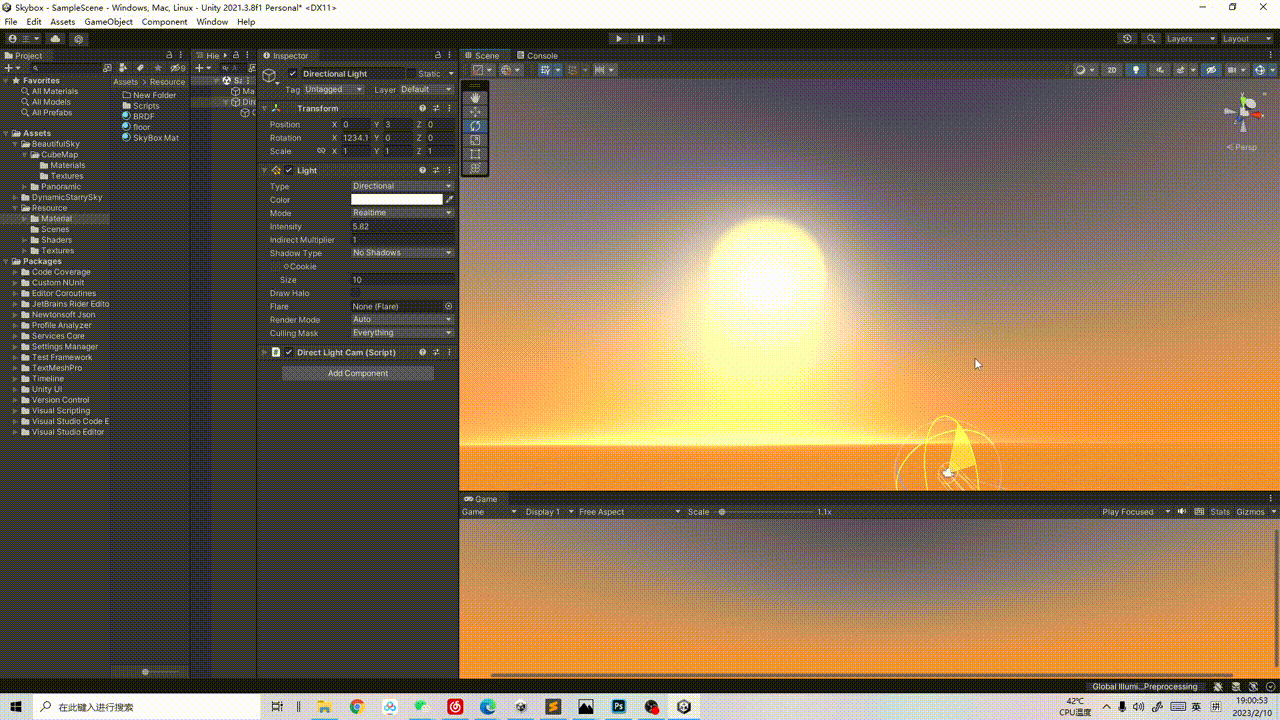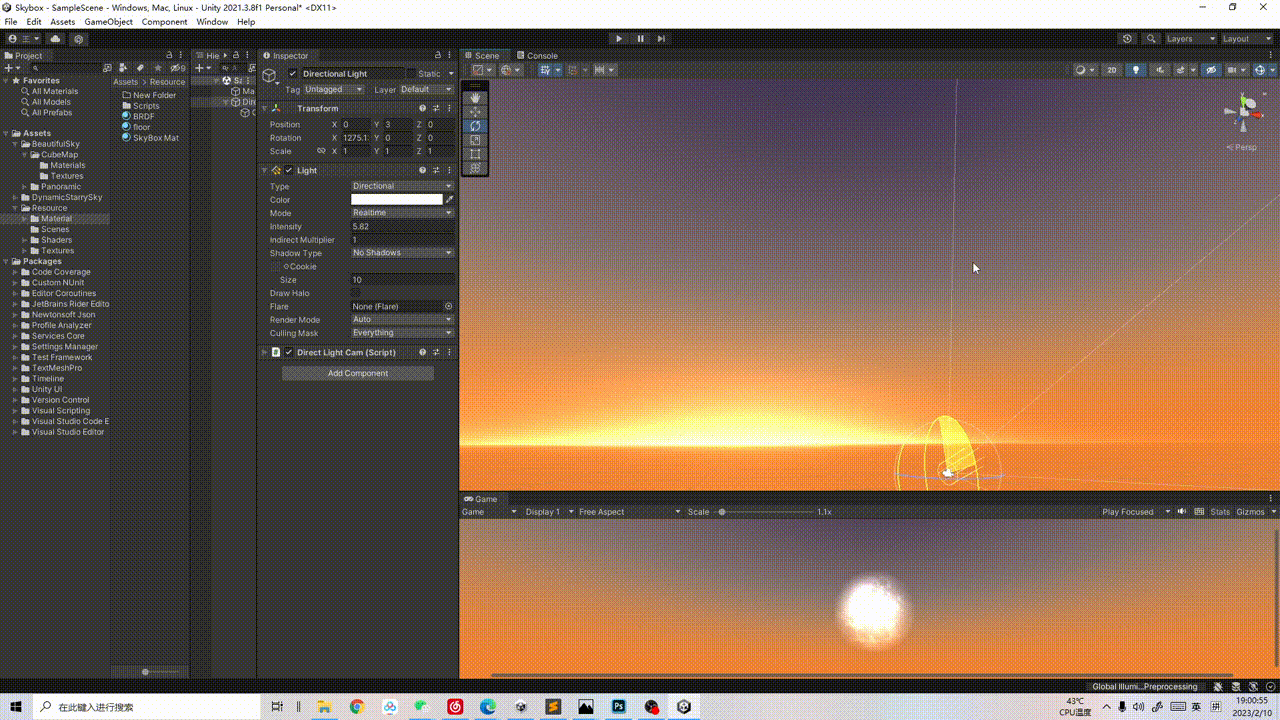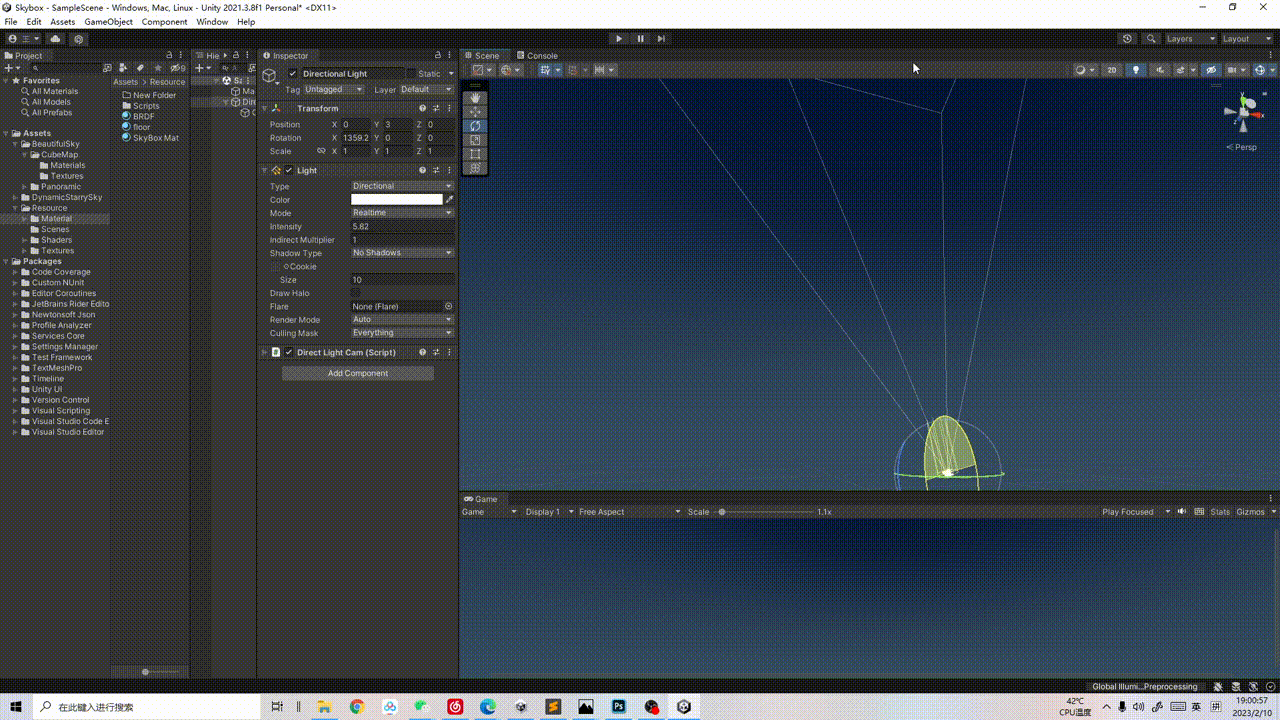
【程序化天空盒】过程记录01:日月 天空渐变 大气散射
1 日月 SunAndMoon 昼夜的话肯定少不了太阳和月亮,太阳和月亮实现的道理是一样的,只不过是月亮比太阳多了一个需要控制月牙程度(or添加贴图)的细节~ 1.1 Sun 太阳的话很简单,直接在shader里实现一个太阳跟随平行光旋…...
无线通信中的轨道角动量
目录 一. 前言 二. 如何传输 三. 如何产生 3.1 螺旋结构器件 (1)螺旋相位板 (2)螺旋抛物面天线 3.2 超表面 3.3 天线阵列 3.3.1 相控阵 3.3.2 时控阵 四. 如何识别 一. 前言 轨道角动量:Orbital Angular M…...
以后更新功能,再也不用App发版了!智能小程序将为开发者最大化减负
在 IoT 时代,越来越多的企业意识到打造自有 App 对于品牌的重要性。作为智能设备不可或缺的控制终端,App 具备连接用户、完善服务、精细化运营用户的独特优势,可帮助企业大大提升品牌竞争力。 为了帮助品牌企业打造更具个性化、差异化的智能…...

C++之类模板全特化和偏特化
类模板类模板是通用类的描述,使用任意类型(泛型)来描述类的定义。使用类模板的时候,指定具体的数据类型,让编译器生成该类型的类定义。注意:函数模板中可以不指定具体数据类型,让编译器自动推到…...
Python 手写数字识别 MNIST数据集下载失败
目录 一、MNIST数据集下载失败 1 失败的解决办法(经验教训): 2 亲测有效的解决方法: 一、MNIST数据集下载失败 场景复现:想要pytorchMINIST数据集来实现手写数字识别,首先就是进行MNIST数据集的下载&am…...
)
华为机试题:HJ61 放苹果(python)
文章目录博主精品专栏导航知识点详解1、input():获取控制台(任意形式)的输入。输出均为字符串类型。1.1、input() 与 list(input()) 的区别、及其相互转换方法2、print() :打印输出。3、整型int() :将指定进制…...
【论文速递】ICCV2021 - 基于超相关压缩实现实时高精度的小样本语义分割
【论文速递】ICCV2021 - 基于超相关压缩的小样本语义分割 【论文原文】:Hypercorrelation Squeeze for Few-Shot Segmentation 【作者信息】:Juhong Min Dahyun Kang Minsu Cho 获取地址:https://openaccess.thecvf.com/content/ICCV2021/…...
)
单例模式(Singleton Pattern)
目录 1.什么是单例模式: 2.单例模式存在的原因: 3.单例模式的优缺点: 4.创建方式: 1. 单线程单例模式立即创建(饿汉式): 2. 单线程单例模式延迟创建(懒汉式)…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...
