25.选择排序,归并排序,基数排序
目录
一. 选择排序
(1)简单选择排序
(2)堆排序
二. 归并排序
三. 基数排序
四. 各种排序方法的比较
(1)时间性能
(2)空间性能
(3)排序方法的稳定性能
(4)关于“排序方法的时间复杂度的下限”
一. 选择排序
(1)简单选择排序
基本思想:在待排序的数据中选出最大(小)的元素放在其最终的位置。
基本操作:
1.首先通过n-1次关键字比较,从n个记录中找出关键字最小的记录,将它与第一个记录交换。
2.再通过n-2次比较,从剩余的n-1个记录中找出关键字次小的记录,将它与第二个记录交换。
3.重复上述操作,共进行n-1趟排序后,排序结束。
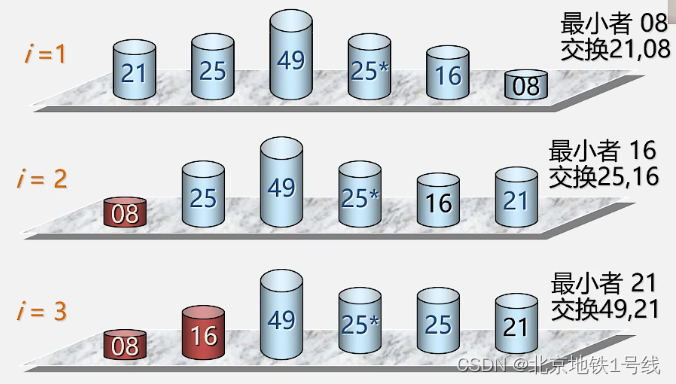

不难写出算法:
void SelectSort(SqList &L){for(i=1; i<L.length; ++i){k=i; //第i趟从第i个元素开始for(j=i+1; j<=L.length; j++)if(L.r[j].key < L.r[k].key) k=j; //记录最小值位置if(k!=i) L.r[i]←—→L.r[k]; //交换}
}
下面我们分析时间复杂度。对移动次数来说,最好情况是0,最坏情况是3(n-1),也就是每一趟都得移动(每次移动需要移动3次)。对比较次数来说,无论待排序列处于什么状态,选择排序所需进行的"比较”次数都相同,为。
上面的算法是不稳定排序(但是可以稳定化)。具体的说用数组实现的选择排序是不稳定的,用链表实现的选择排序是稳定的。例如,给定8,5,8*,7,9;第1次:5,8,8*,7,9;第2次:5,7,8*,8,9;从而可以验证它是不稳定的。
(2)堆排序
堆的定义:若n个元素的序列满足
或
,则分别称该序列为小根堆和大根堆。从堆的定义可以看出,堆实质是满足如下性质的完全二叉树:二叉树中任一非叶子结点均小于(大于)它的孩子结点。
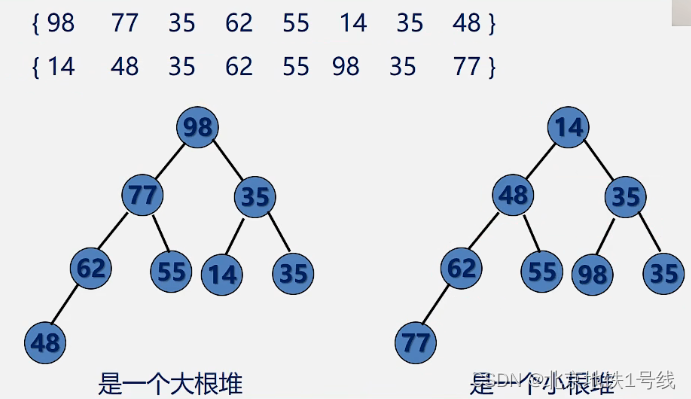
显然,大根堆的根结点是最大值,小根堆的根结点是最小值。若在输出堆顶的最小值(最大值)后,使得剩余n-1个元素的序列又重建成一个堆,则得到n个元素的次小值(次大值)....如此反复,便能得到一个有序序列,这个过程称之为堆排序。
那么怎么重建呢?以小(大)根堆为例:
1.输出堆顶元素之后,以堆中最后一个元素(编号最大的元素)替代之;
2.然后将根结点值与左、右子树的根结点值进行比较,并与其中小(大)者进行交换;
3.重复上述操作,直至叶子结点,将得到新的堆,称这个从堆顶至叶子的调整过程为“筛选”。
例如,对下面的小根堆,把13输出,最后一个元素97作为根结点,它的左右孩子是38和27,27较小,所以把97和27交换。此时97的左右孩子是65和49,49较小,把49和97交换,这个时候97已经是叶子结点就不用再操作了。
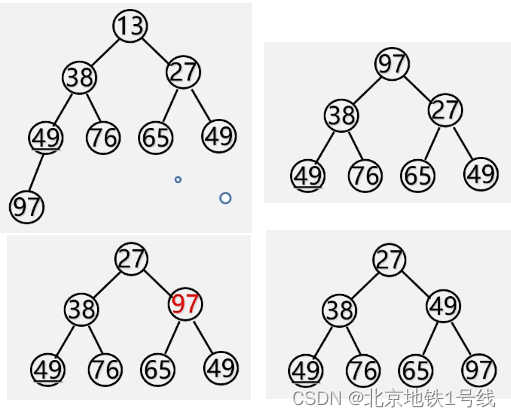
写出算法如下:
void HeapAdjust(elem R[], int s, int m){
/*已知R[s..m]中记录的关键字除R[s]之外均满足堆的定义,本函数调整R[s]的关键字,使R[s..m]成为一个大根堆*/rc = R[s];for (j=2*s; j<=m; j *= 2){ //沿key较大的孩子结点向下筛选if (j < m && R[j] < R[j+1]) ++j; //j为key较大的记录的下标if (rc >= R[j]) break; //rc大于左右孩子,这个时候已经符合要求,就不用做了R[s] = R[j]; //较大的孩子结点往上升s = j; //rc应插入在位置s上,更新s}//forR[s] = rc; //插入
}//HeapAdjust
HeapAdjust函数是一个用于调整堆的函数。它接受一个数组R,以及两个整数s和m作为参数。s表示要调整的子树的根节点的位置,m表示该子树的最后一个节点的位置。
首先,将根节点的值保存在变量rc中。然后,通过一个循环来比较根节点和其子节点的值。在循环中,变量j初始化为根节点的左子节点的位置(2*s),然后每次乘以2,即可得到下一个子节点的位置。在循环中,首先判断是否存在右子节点,并且右子节点的值是否大于左子节点的值。如果满足条件,则将j加1,即将j指向右子节点。然后,判断rc的值是否大于等于R[j]的值。如果满足条件,则退出循环。如果rc的值小于R[j]的值,则将R[j]的值赋给R[s],即将较大的子节点的值上移到根节点的位置。然后,将s更新为j,即将s指向较大子节点的位置。循环结束后,将rc的值赋给R[s],即将根节点的值放到合适的位置上。这样,HeapAdjust函数完成了对以s为根节点的子树的调整,使其满足堆的性质。
可以看出:对一个无序序列反复“筛选”就可以得到一个堆。即:从一个无序序列建堆的过程就是一个反复“筛选”的过程。我们重新考察堆的定义,显然:单结点的二叉树是堆,在完全二叉树中所有以叶子结点(序号i > n/2,这里是整除向下取整)为根的子树也是堆。这样,我们只需依次将以序号为n/2,n/2 - 1,.....1的结点为根的子树均调整为堆即可。即:对应由n个元素组成的无序序列,“筛选”只需从第n/2个元素开始。
由于堆实质上是一个线形表,那么我们可以顺序存储一个堆。下面以一个实例介绍建一个小根堆的过程。例如给定关键字为49,38,65,97,76,13,27,49的一组记录,将其按关键字调整为一个小根堆:
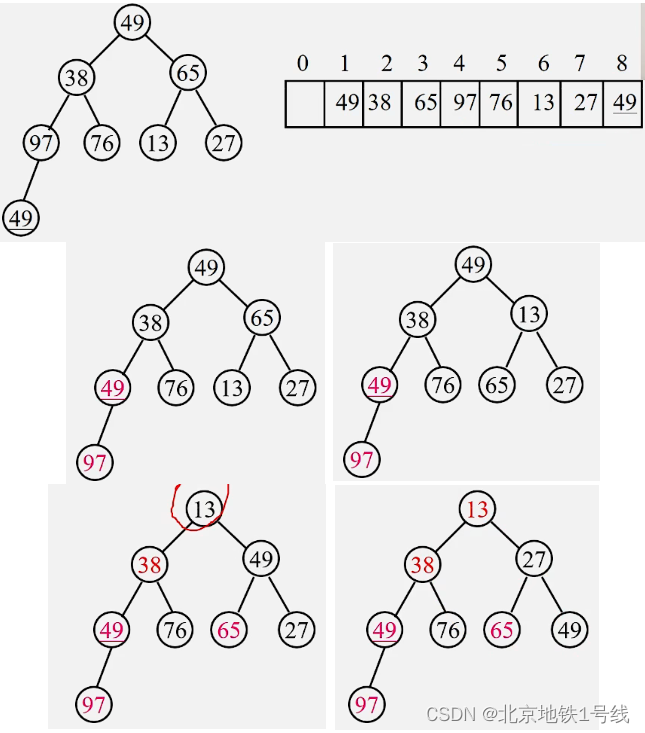
将初始无序的R[1]到R[n]建成一个小根堆,可用以下语句实现:
for(i = n/2 ; i >= 1; i--)HeapAdjust (R, i, n);上面我们了解了怎么建堆。若对一个无序存列建堆,然后输出根。重复该过程就可以由一个无需序列输出有序序列。实质上,堆排序就是利用完全二叉树中父结点与孩子结点之间的内在关系来排序的。
void HeapSort(elem R[]){ //对R[1]到R[n]进行堆排序int i;for (i = n/2; i>= 1; i--)HeapAdjust(R, i, n);//建初始堆for (i = n; i > 1; i--){ //进行n-1趟排序Swap(R[1], R[i]); //根与最后一个元素交换,也就是把根结点输出并放在最后一个位置HeapAdjust(R, 1, i-1); //对R[1]到R[i-1]重新建堆}
}//HeapSort
最后我们来研究时间复杂度。初始堆化所需时间不超过O(n),排序阶段(不含初始堆化)每次重新堆化所需时间不超过O(logn),则n-1次循环所需时间不超过O(nlogn)。因此:
Tw(n)=O(n)+ O(nlogn)= O(nlogn)
堆排序的时间主要耗费在建初始堆和调整建新堆时进行的反复筛选上。堆排序在最坏情况下,其时间复杂度也为O(nlog2n),这是堆排序的最大优点。无论待排序列中的记录是正序还是逆序排列,都不会使堆排序处于"最好"或"最坏"的状态。另外,堆排序仅需一个记录大小供交换用的辅助存储空间。
然而堆排序是一种不稳定的排序方法,它不适用于待排序记录个数n较少的情况,但对于n较大的文件还是很有效的。
二. 归并排序
基本思想:将两个或两个以上的有序子序列“归并”为一个有序予列。在内部排序中,通常采用的是2-路归并排序。即:将两个位置相邻的有序子序列R[1..m]和R[m+1..n]归并为一个有序序列R[1..n]。
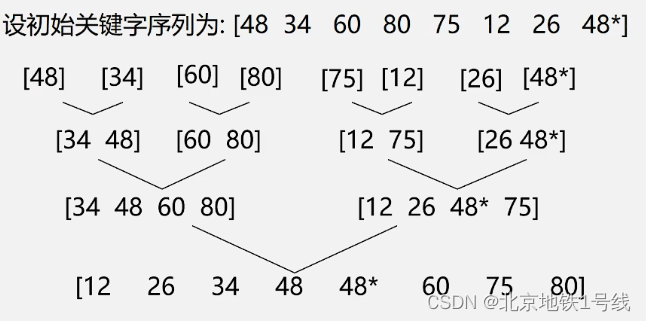
这种树称为归并树。n个元素归并排序只需要趟。下面讨论怎么把两个有序序列合并成一个有序序列。这里可以参考线性表的合并算法。设R[low]-R[mid]和R[mid+1]-R[high]为相邻,归并成一个有序序列R1[low] - R1[high].

若SR[i].key<=SR[j].key,则TR[k]=RS[i];k++;i++; 否则,TR[k]=SR[j];k++;j++;
归并排序的时间效率是O(nlog2n),空间效率是O(n),因为需要一个与原始序列同样大小的辅助序列(TR)。这正是此算法的缺点。归并排序算法是稳定的算法。
三. 基数排序
基本思想:分配+收集
基数排序也叫桶排序或箱排序:设置若干个箱子,将关键字为k的记录放入第k个箱子,然后在按序号将非空的连接。基数排序的数字是有范围的,均由0-9这十个数字组成,则只需设置十个箱子,相继按个、十、百...进行排序。例:给定待排序序列(614,738,921,485,637,101,215,530,790,306)。这里每一个箱子都是一个队列,遵循先进先出的原则:
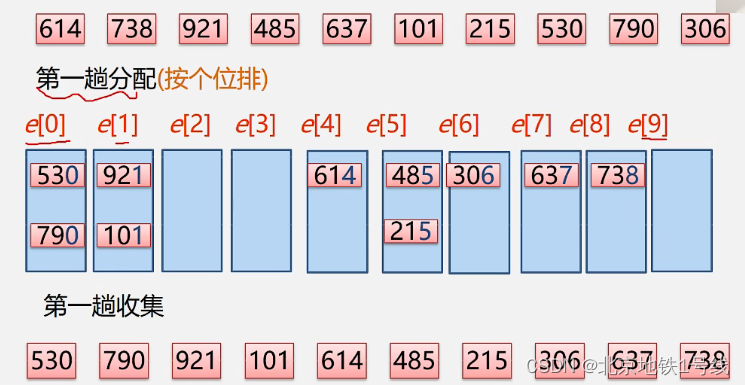
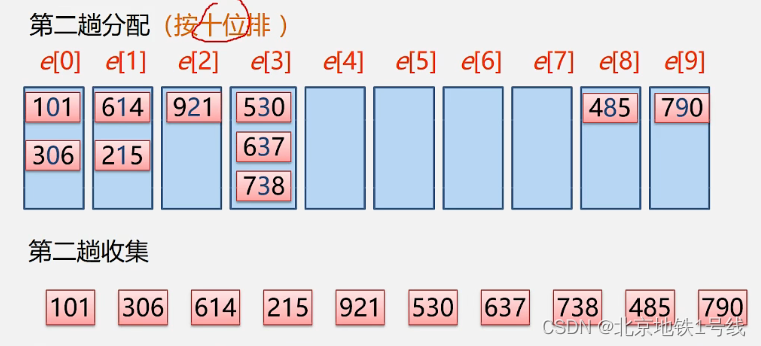

至此排序完成!基数排序的时间效率:O(k*(n+m)),其中k:关键字个数(上面有3个关键字),m:关键字取值范围为m个值(上面为10),n:元素个数。这里,每一趟分配n个元素,收集m个桶,总共需要k遍。
空间效率:这里需要放置m个桶,回收的时候回收n个元素,则空间复杂度是O(n+m)。基数排序是稳定的。
四. 各种排序方法的比较
(1)时间性能
1.按平均的时间性能来分,有三类排序方法:
- 时间复杂度为O(nlogn)的方法有:快速排序、堆排序和归并排序,其中以快速排序为最好;
- 时间复杂度为O(n^2)的有:直接插入排序、冒泡排序和简单选择排序,其中以直接插入为最好,特别是对那些对关键字近似有序的记录序列尤为如此;
- 时间复杂度为O(n)的排序方法只有:基数排序。
2.当待排记录序列按关键字顺序有序时,直接插入排序和冒泡排序能达到到O(n)的时间复杂度;而对于快速排序而言,这是最不好的情况,此时的时间性能退化为O(n^2),因此是应该尽量避免的情况。
3.简单选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布而改变。
(2)空间性能
指的是排序过程中所需的辅助空间大小.
1.所有的简单排序方法(包括:直接插入、冒泡和简单选择)和堆排序的空间复杂度为O(1)
2.快速排序为O(logn),为栈所需的辅助空间
3.归并排序所需辅助空间最多,其空间复杂度为O(n)
4.链式基数排序需附设队列首尾指针,则空间复杂度为O(rd)
(3)排序方法的稳定性能
稳定的排序方法指的是,对于两个关键字相等的记录,它们在序列中的相对位置,在排序之前和经过排序之后,没有改变。
- 当对多关键字的记录序列进行LSD方法排序时,必须采用稳定的排序方法。
- 对于不稳定的排序方法,只要能举出一个实例说明即可。
- 快速排序和堆排序是不稳定的排序方法。
(4)关于“排序方法的时间复杂度的下限”
本章讨论的各种排序方法,除基数排序外,其它方法都是基于“比较关键字”进行排序的排序方法,可以证明,这类排序法可能达到的最快的时间复杂度为O(nlogn)。(基数排序不是基于“比较关键字”的排序方法,所以它不受这个限制)。
可以用一棵判定树来描述这类基于“比较关键字”进行排序的排序方法。
相关文章:

25.选择排序,归并排序,基数排序
目录 一. 选择排序 (1)简单选择排序 (2)堆排序 二. 归并排序 三. 基数排序 四. 各种排序方法的比较 (1)时间性能 (2)空间性能 (3)排序方法的稳定性能…...

DataX DorisWriter 插件DorisStreamLoadObserver类详细解读
DorisStreamLoadObserver 类是一个用于将数据加载到 Doris(以前称为 Palo)数据库中并监视加载过程的 Java 类。该类提供了一组方法,用于构建 HTTP 请求、处理 HTTP 响应以及监控数据加载的状态。以下是每个方法的具体作用: Doris…...
leetcode:1710. 卡车上的最大单元数(python3解法)
难度:简单 请你将一些箱子装在 一辆卡车 上。给你一个二维数组 boxTypes ,其中 boxTypes[i] [numberOfBoxesi, numberOfUnitsPerBoxi] : numberOfBoxesi 是类型 i 的箱子的数量。numberOfUnitsPerBoxi 是类型 i 每个箱子可以装载的单元数量。…...

Spring_JDBC的使用
Spring 是个一站式框架:Spring 自身也提供了控制层的 SpringMVC和持久层的 Spring JdbcTemplate。 配置信息 1.下载 Spring JdbcTemplate 的 jar 包,在pom.xml中导入 <dependency><groupId>org.springframework</groupId><artifactId>spr…...
【Python从入门到进阶】34、selenium基本概念及安装流程
接上篇《33、使用bs4获取星巴克产品信息》 上一篇我们介绍了如何使用bs4来解析星巴克网站,获取其产品信息。本篇我们来了解selenium技术的基础。 一、什么是selenium? Selenium是一种用于自动化Web浏览器操作的开源工具。它提供了一组API(应…...

如何确保ChatGPT在文本生成中遵循道德和伦理准则?
确保ChatGPT在文本生成中遵循道德和伦理准则是一个复杂而重要的任务。人工智能(AI)系统,特别是语言模型,具有强大的生成能力,但如果不受到道德和伦理准则的约束,可能会导致一系列问题,包括歧视、…...

RISC-V Linux系统rootfs制作
文章目录 1、下载2、配置与编译3、运行 buildroot 是一个构建嵌入式Linux系统的框架。整个 buildroot 是由Makefile(*.mk) 脚本和 Kconfig(Config.in) 配置文件构成的,因此可以像配置 Linux 内核一样执行 make menuconfig 进行配置,编译出一个完整的、可…...

git常用场景记录 | 拉取远程分支A合并到本地分支B
文章目录 git常用场景记录拉取远程分支A合并到本地分支B本地分支B存在未add与commit的代码 git常用场景记录 doing,最后更新9.1 拉取远程分支A合并到本地分支B 需求描述 在团队合作时,我自己的本地分支B功能已经实现并合并到feature,之后发现…...

如何利用Linux进行数据管理和分析?
Linux是一款非常强大的操作系统,它不仅可以帮助你管理数据,还可以让你成为一名数据分析大师。只要你会使用命令行,你就可以用Linux进行数据管理和分析。 现在,让我们来看看如何使用Linux进行数据管理。 使用sort命令对数据进行排…...

vue3封装echarts图表数据无法渲染到页面
问题是后端的数据已经成功返回到前端了,但是Echarts图表一直不能被渲染,卡了一个多小时,最后问gpt才解决(gptyyds!!!) methods: {loadGet() {this.$axios.get(this.$httpUrl /goods…...

MySQL索引,事务和存储引擎
一、索引 1、索引的概念 ●索引是一个排序的列表,在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址(类似于C语言的链表通过指针指向数据记录的内存地址)。 ●使用索引后可以不用扫描全表来定位某行的数据,而是先…...

开发指导—利用CSS动画实现HarmonyOS动效(一)
注:本文内容分享转载自 HarmonyOS Developer 官网文档 一. CSS 语法参考 CSS 是描述 HML 页面结构的样式语言。所有组件均存在系统默认样式,也可在页面 CSS 样式文件中对组件、页面自定义不同的样式。请参考通用样式了解兼容 JS 的类 Web 开发范式支持的…...
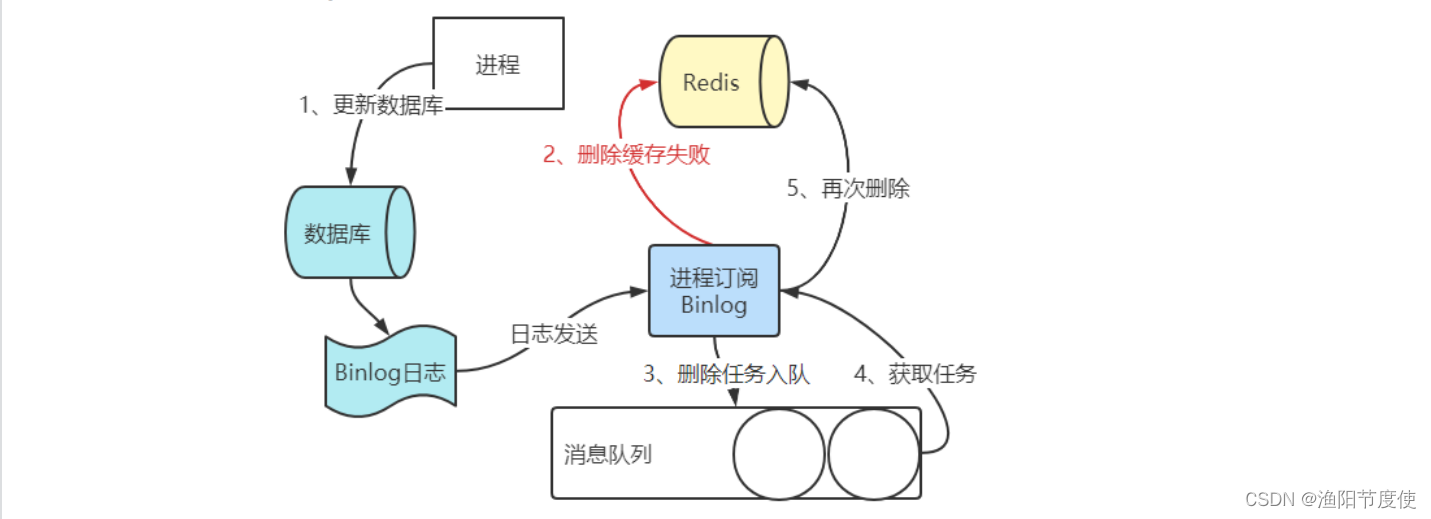
电商项目part10 高并发缓存实战
缓存的数据一致性 只要使用到缓存,无论是本地内存做缓存还是使用 redis 做缓存,那么就会存在数据同步的问题。 先读缓存数据,缓存数据有,则立即返回结果;如果没有数据,则从数据库读数据,并且把…...

MongoDB实验——MongoDB shell操作
MongoDB shell操作 实验原理 MongoDB shell是一个可执行文件,是MongoDB自带的一个交互式JavaScript shell,位于MongoDB安装路径下的/bin文件夹中。要启动MongoDB shell,可执行命令mongo。这将在控制台提示符中启动该shell,Mongo…...
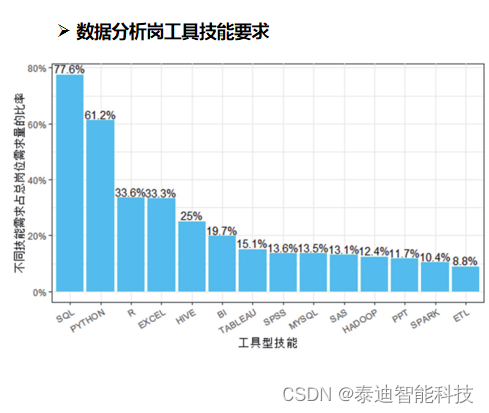
数据分析师职业发展道路,工作内容是什么?
很多同学问,参加数据分析就业班后之的就业发展道路是怎样的,工作又能做什么呢? 市面上的常见的工作类型有有运营类、技术类及分析类等,可以根据自己的意愿去做适合自己的工作,但是任何工作其实都是需要一技之长。…...

Vue3 + ts的使用
一. IDE的配置 1. VSCode 插件安装搜索builtin typescript 2. 点击“TypeScript and JavaScript Language Features”右下角的小齿轮,然后选择“Disable (Workspace)” 3. 重新加载工作空间。Takeover 模式将会在你打开一个 Vue 或者 TS 文件时自动启用。 二. 依赖的…...

CF Edu152 C
Problem - C - Codeforces 题意: 思路: 首先,观察样例可知 这种是等效的 推广一下 0000.....111111 ..l..............r...... 这种是等效的 容易想到维护后面第一个1的位置和前面第一个0的位置,然后把所有区间都等效一下&…...

iBooker 技术评论 20230902
一、女子同时供职 16 家公司却从不上班,全国骗薪群体至少有七八百人,为何会出现此类骗薪群体? 社保其实很好绕过。就是这些骗薪者一起创立一个外包公司,然后通过这个公司把自己外包出去。这些人和外包公司签的是劳务合同…...

视频动态壁纸 Dynamic Wallpaper for Mac中文
Dynamic Wallpaper是一款Mac平台上的动态壁纸应用程序,它可以根据时间等因素动态切换壁纸,提供更加生动和多样化的桌面体验。 Dynamic Wallpaper包含了多个动态壁纸,用户可以根据自己的喜好选择和切换。这些动态壁纸可以根据时间等因素进行自…...
Java“牵手”京东商品列表数据,关键词搜索京东商品数据接口,京东API申请指南
京东商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取京东商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问京东商城的网页来获取商品详情信息。以下是两种常用方法的介绍&…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
