编程题四大算法思想(三)——贪心法:找零问题、背包问题、任务调度问题、活动选择问题、Prim算法
文章目录
- 贪心法
- 找零问题(change-making problem)
- 贪心算法要求
- 基本思想
- 适合求解问题的特征
- ==背包问题==
- 0/1背包问题
- 0/1背包问题——贪心法
- 分数背包问题
- 任务调度问题
- 活动选择问题
- 活动选择——贪心法
- 最早结束时间优先——最优性证明
- ==Prim算法==
贪心法
我在当前情况下,我把我做到最好。我也不管全局如何,整体如何。我就考虑我现在的这一个,或者这一小部分怎样最好。
- 贪心技术是一种设计算法的通用策略。
- 贪心技术的基本思想:
- 基于贪心选择准则,每次得到局部最优的选择。
- 希望利用局部最后得到全局最优解。
- 贪心选择性质:局部最优可以得到全局最优。
- 找到正确的贪心选择准则是设计贪心算法的关键。
- 不同的贪心选择准则可以得到不同的结果。
打个比方,我现在有几种选择:
学编程、打游戏、读书、去外面玩、去兼职、……
如果我的目的是提高自己的知识水平,那起码对于现在的这些选择来说,我选择“学编程”或者“读书”就是最优的。
只是说当前这一步怎么走是最优的,也并没有去管后面的路怎么走。
比如你说选择“打游戏”,后面可能也会更成功,但是不管这个。
找零问题(change-making problem)
- 给定无限多不同面额的硬币 d 1 > . . . > d m d_1>...>d_m d1>...>dm,对于总额 n n n,如何找到最少的硬币数目?
- 问题:目标函数和约束条件是什么?
例如:
d 1 = 25 c , d 2 = 10 c , d 3 = 5 c , d 4 = 1 c ,而且 n = 48 c d_1=25c,d_2=10c,d_3=5c,d_4=1c,而且n=48c d1=25c,d2=10c,d3=5c,d4=1c,而且n=48c。
我们可能想,要使得硬币数目最少,那简单啊。
先紧着面额最大的来凑就行了。
先拿个25c的、再拿两个10c的,5c的没法拿,于是再拿3个1c的。
于是得到贪婪解:
<1,2,0,3>。我们这个策略就是,很简单,先紧着最大的拿。
但是我们虽然这样做了,而且貌似可行。
但是实际上,它对于大多数情况而言,这样可能是没问题的;但是没法保证所有情况啊,你没法保证对于所有情况、任意某一种情况,这样都没问题。
有一些情况,你这样做,可能就压根不是最优解了。
但是:
- 对大多数常用的硬币面额都可以得到最优解。
- 对任意硬币面额,有可能不是最优解。
例如:
d 1 = 25 c , d 2 = 10 c , d 3 = 1 c 而且 n = 30 c d_1=25c,d_2=10c,d_3=1c而且n=30c d1=25c,d2=10c,d3=1c而且n=30c。
那么你还按照上面的规则,
先拿个25c的,然后拿五个1c的。——此时是6个硬币。
但实际上我们可以看出,直接拿三个10c的就够了,而且只用3个硬币。
所以可见,我们刚才的那种简单的想法:先紧着大面额的拿。
这种方法,可能在某些情况下没毛病,但是在有些情况下就不对了、不是最优解了。
**那咋办呢。**是不是我的想法、我的策略设计的有问题呢?
那到底咋样弄,才能对于所有情况都能得到最优解呢?
我们可以用回溯法。(不是讲贪心吗,咋又说回溯了?——后面再说这个问题)
- **贪婪法:**建议通过一系列步骤来构造问题的解,每一步对目前构造的部分解做一个扩展,直到获得问题的完全解。(完全解,不是最优解)
- 必须满足:可行、局部最优、不可取消。
贪心算法要求
- 可行的:即它必须满足问题的约束。
- 局部最优:它是当前步骤中所有可行选择中最佳的局部选择。
- 不可取消:即选择一旦做出,在算法的后面步骤中就无法改变了。
就像人生中的一些选择一样,就是贪心算法么,每次选的是局部最优,而且选了之后就没法取消了。
在每一步中,它要求“贪婪”地选择最佳操作,并希望通过一系列局部的最优选择,能够产生一个整个问题的(全局的)最优解。
基本思想
- 从问题的某一个初始解出发,通过一系列的贪心选择(当前状态下的局部最优选择),逐步逼近给定的目标,尽可能快地求得更好的解。
- 在贪心算法(greedy method)中也采用逐步构造最优解的方法。在每个阶段,都做出一个按某个评价函数最优的决策,该评价函数最优称为贪心准则(greedy criterion)。
- 贪心算法的正确性,就是要证明按贪心准则求得的解是全局最优解。
- 贪心算法不能对所有问题都得到全局最优解。
- 但是对于许多问题,它能够产生全局最优解。如单源最短路径问题,最小生成树问题等。
适合求解问题的特征
- **贪心选择性质:**可通过局部最优(贪心)选择达到全局最优解。
- 通常以自顶向下的方式进行,每次选择后将问题转化为规模更小的子问题。
- 该性质是贪心法使用成功的保障,否则得到的是近优解。
- 最优子结构性质:问题的最优解包含它的子问题的最优解。
- 并不是所有具有最优子结构性质的问题都可以采用贪心策略。
- 往往可以利用最优子结构性质来证明贪心选择性质。
背包问题
- 0-1背包问题
给定n种物品和一个背包。物品i的重量是 W i W_i Wi,其价值为 V i V_i Vi,背包的容量为C。应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
0-1背包问题,对于一个物品,0就是不拿它,1就是拿它。
在选择装入背包的物品时,对每种物品只有两种选择,要么装入背包、要么不装入背包。不能将一个物品装入背包多次,也不能只装入某物品的一部分。
- 背包问题
与0-1背包问题类似,所不同的是,在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,1≤i≤n。
背包问题,也叫“分数背包问题”,对于一个物品,物品太大了,背包剩余空间不够了,此时我可以把物品拆下来、把一部分放进去。
0/1背包问题
- 已知
- 背包容量C>0
- n个物品,体积 w i > 0 w_i>0 wi>0,价值 p i > 0 f o r i = 1 , . . . , n p_i>0\ for\ i=1,...,n pi>0 for i=1,...,n
- 确定 { 1 , 2 , . . . , n } \{1,2,...,n\} {1,2,...,n}的子集,满足:
m a x ∑ i ∈ A p i , s u b j e c t t o ∑ i ∈ A w i ≤ C max\sum_{i∈A}p_i,subject\ to\ \sum_{i∈A}w_i≤C maxi∈A∑pi,subject to i∈A∑wi≤C
0/1背包问题——贪心法
-
有以下几种贪心选择准则:
- 最大价值优先——先选择最值钱的物品。
紧着最值钱的先往上放。
- 最小体积优先
紧着最小体积的先放,想装的多。
- 最大体积优先
想着一般大的东西都比较值钱?所以先紧着大件先放?
- 最大单位价值优先
这四个规则都有一定道理,那我们该选哪种呢?选最大价值优先?选最大单位价值优先?
- 没有一种方法能保证得到最优解
最大价值优先

(lb是重量单位,上面是价钱)
可见,最大价值优先,放进来的不一定是最优解。
最小体积优先

可见,最小体积优先,放进来的也不一定是最优解。
最大体积优先
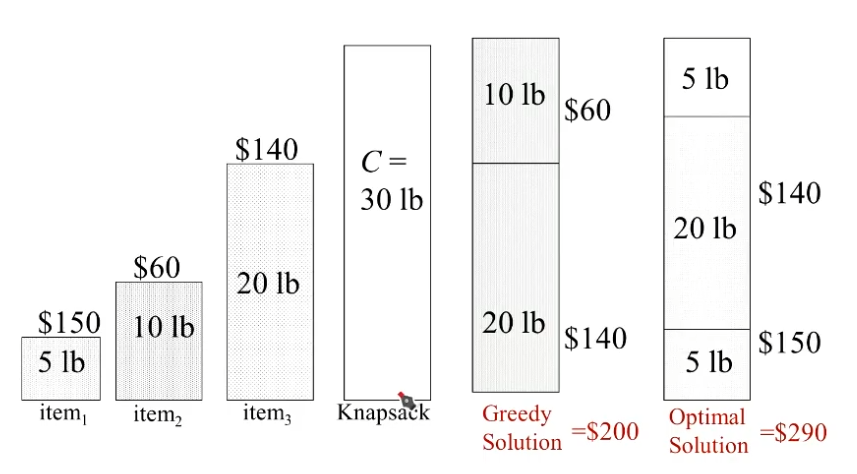
可见,最大体积优先得到的也不一定是最优解。
最大单位价值优先
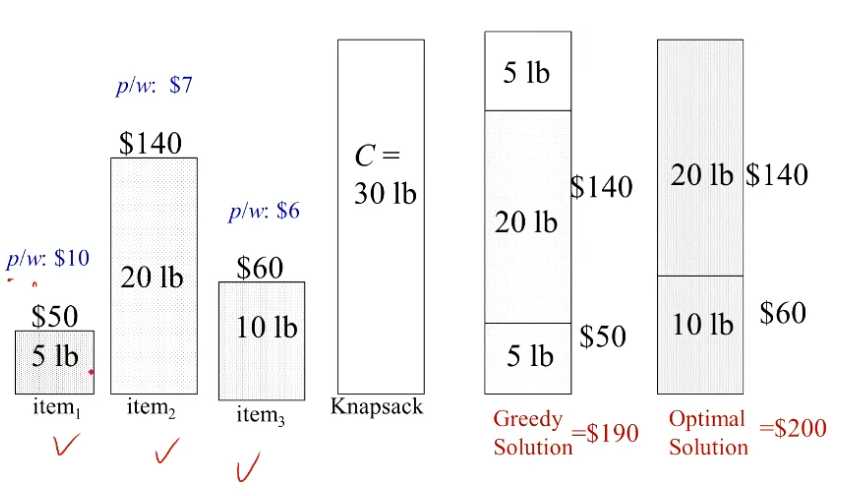
可见,这个也不一定能得到最优解。
分数背包问题
- 对于0/1背包问题,没有最优的贪心算法。
- 分数背包问题:可以将第
i个物品的一部分放入背包。 - 对于分数背包问题,贪心算法是其不二选择,该算法基于最大单位价值的选择准则。(感觉有点类似于微积分里的微元思想)
这个就没啥好犹豫的了,我先紧着最大单位价值的往里面放,放不下整个物品的时候,我把当前最大单位价值的物品切出来一块往里面放。
这样最后包里放的肯定是价值最大的情况。
- 贪心算法过程:
- 降序排序 v i / w i v_i/w_i vi/wi。
- 根据排序次序增加物品,直到这个物品装完,或是超出背包容量。
- 如果背包没有满,选择下一个物品开始装。
最优解证明
- 证明:
我们首先假设我们有一个最优解 A 1 A_1 A1,那么我们首先找到 A 1 A_1 A1里面平均价值最高的物品 a m a_m am,然后我们将用商品里面平均价值最高的物品 a 1 a_1 a1将 a m a_m am进行全部替换或者部分替换得到解 A 2 A_2 A2,又因为 v 1 w 1 ≥ v m w m \frac{v_1}{w_1}≥\frac{v_m}{w_m} w1v1≥wmvm,所以 A 2 A_2 A2的总价值高于 A 1 A_1 A1的总价值,这与 A 1 A_1 A1是最优解矛盾,于是得到 A 1 A_1 A1里面包含平均价值最高的物品。
- 小数背包问题还具有贪心选择性质,用贪心法求解更简单、更快速。
- 0-1背包问题用贪心法求解不一定能得到最优解。
任务调度问题
- 9个任务需要调度,每个任务运行时间为
3,5,6,10,11,14,15,18,20
如果只有一个处理器,那就没啥说的,每个任务看看按照什么规则往里放就行了,反正最后总时间是一样的。
但是如果有多个处理器呢?
- 有三个处理器执行这些任务。
当然,对于贪心而言,我们对这一问题也可以有很多种贪心策略。
- 贪心准则:先运行时间最长的任务。
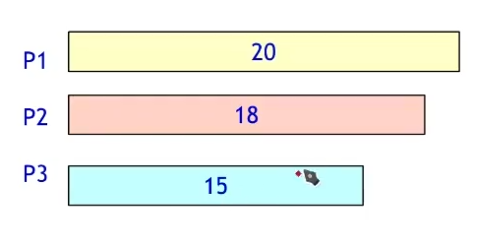
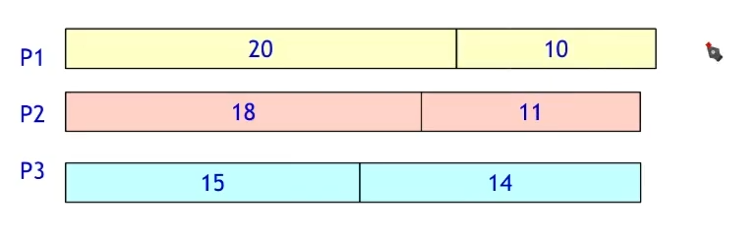
每次把当前需要运行最长时间的任务,分配给当前任务时间最短的处理器。

因此,三个处理器执行这些任务,花费35分钟时间。
这个解决方法不错,但是我们可能还可以有更好的策略。
- 另一种贪心准则:优先运行最短任务
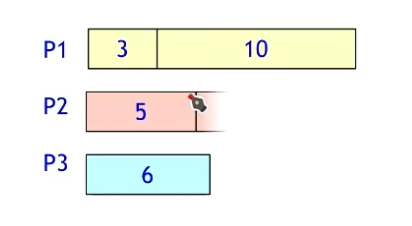

这个方式还不如刚才那个,这个需要花费40分钟。
最优解

折腾半天都不是最好的,那我们看看最优解到底是什么样的,如上图所示。
- 这个解为什么是最优的?
很明显么。因为三个处理器刚好平均分了所有任务的总时长,没有任何的浪费。
但是,可见,若想得到这样的一种解。你要付出的代价就会很高了。
有必要么,实际解决一个问题来说,这样去搞,可能没这个必要。你找到最优解了之后,最优解固然能够帮你节约时间;但是不要忽视了,你寻找这个最优解也要花时间。你为了找一个最优解去节约那一点点时间,然后你花了大量的时间在寻找到最优解上,得不偿失。
类似上图中这个最优解,是咋找到的?可能是暴力穷举吧,或者是什么方法。总之很耗时间才能找出来的。
实际上我就用一种贪心策略,去做,就拉倒了。虽然可能不是最优,但是接近最优差不多就行了。
对于一些特殊的问题,贪心算法能直接找出其最优解,能直接获取最优解那当然更好了。
总之贪心算法可能找到的不是最优解,而只是局部最优解;但是它的实现是很简单的,不会耗费太多时间。
同时,我们在贪心,贪的过程中,也可以利用回溯法的思想,对一些没必要继续探讨下去的情况进行剪枝,而没必要全部贪到底、再去排除。也就是贪心法配合回溯法进行使用。
活动选择问题

- 这个就是活动选择问题。
我选择哪些活动,能够让活动数量最多?


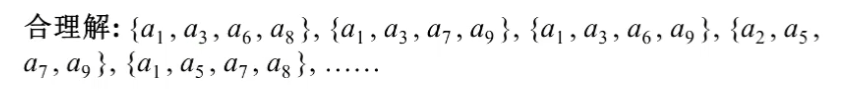
活动选择——贪心法
- 贪心法选择准则:
- 最早开始时间优先
- 最小持续时间优先
- 最早完成时间优先
- 哪个准则更有效?

最早开始时间优先。
假设有一个从0开始的活动,但是它持续时间巨长。
那这显然不是最优解。
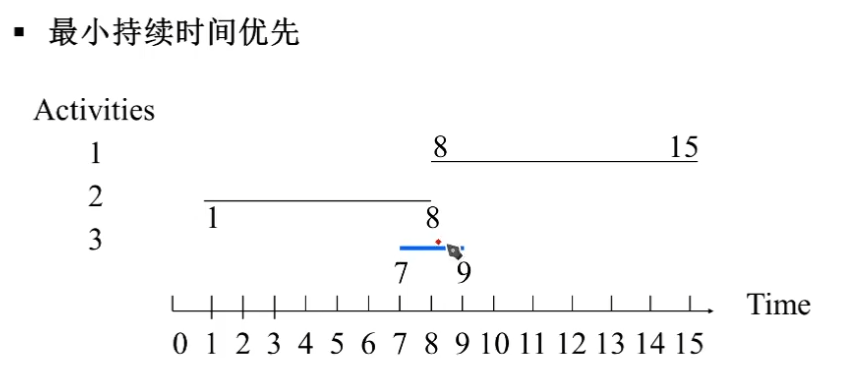
如上图。
这个持续时间最小,但是可能因为做了它,它刚好介于两个活动邻接点,导致两个活动都没法做。
显然也不是最优解。


最早结束时间是不是能达到这个问题的最优解?
实际上,按最早结束时间优先,基本上都能取到最优解。
怎么证明这种策略的正确性?怎么知道上面的例子不是它的特例?
- 需要证明贪心法的正确性。
最早结束时间优先——最优性证明
**定理:**如果活动 a 1 a_1 a1在所有活动中具有最早结束时间,则最优解中一定包含 a 1 a_1 a1。
证明:
- 令 A A A是最优解, a 1 a_1 a1是贪心法选择的最早结束时间的活动。如果 a 1 ∈ A a_1∈A a1∈A,则定理得证。
- 如果 a 1 ∉ A a_1∉A a1∈/A,我们证明 A ∗ = A − { a } + { a 1 } A^*=A-\{a\}+\{a_1\} A∗=A−{a}+{a1}是另一个包含 a 1 a_1 a1的最优解,而 a a a是 A A A中具有最早结束时间的活动。
- 因为活动的结束时间已排序好, f ( a 1 ) ≤ f ( a ) f(a_1)≤f(a) f(a1)≤f(a)。假设 f ( a 1 ) ≤ s ( a ) f(a_1)≤s(a) f(a1)≤s(a),如果我们把 a 1 a_1 a1加到 A A A,意味着 A A A不是最优的。所以 s ( a ) < f ( a 1 ) s(a)<f(a_1) s(a)<f(a1),并且 a 1 a_1 a1和 a a a重叠。因为 f ( a 1 ) ≤ f ( a ) f(a_1)≤f(a) f(a1)≤f(a),如果我们移除 a a a添加 a 1 a_1 a1,可以得到另一个最优解 A ∗ A^* A∗包含了 a 1 a_1 a1。 A ∗ A^* A∗是最优的,因为 ∣ A ∗ ∣ = ∣ A ∣ |A^*|=|A| ∣A∗∣=∣A∣。
没太看懂。
**定理:**贪心子选择一定产生最优解。
即,证明去掉一个 a 1 a_1 a1之后,对剩下的活动做最早结束时间优先策略,得到的也是子集的最优解。
证明:
- 令 a 1 a_1 a1是贪心算法选择的活动。
- 令 S ∗ S^* S∗是不与 a 1 a_1 a1重叠的活动子集
S ∗ = { a i ∣ i = 2 , . . . , n a n d s i ≥ f ( a 1 ) } S^*=\{a_i | i=2,...,n\ and\ s_i≥f(a_1)\} S∗={ai∣i=2,...,n and si≥f(a1)}
-
令 B B B是 S ∗ S^* S∗的最优解。
-
从 S ∗ S^* S∗的定义可知, A ∗ = { a 1 } ∪ B A^*=\{a_1\}∪B A∗={a1}∪B是可行的,并且是原问题的解。
-
利用反证法证明 A ∗ A^* A∗是最优解。
-
假设 A ∗ A^* A∗不是最优解,令 A A A是包含 a 1 a_1 a1的最优解,则 ∣ A ∗ ∣ < ∣ A ∣ |A^*|<|A| ∣A∗∣<∣A∣,且 ∣ A − { a 1 } ∣ > ∣ A ∗ − { a 1 } ∣ = ∣ B ∣ |A-\{a_1\}|>|A^*-\{a_1\}|=|B| ∣A−{a1}∣>∣A∗−{a1}∣=∣B∣。
-
但是 A − { a 1 } A-\{a_1\} A−{a1}也是 S ∗ S^* S∗的解,与 B B B是 S ∗ S^* S∗的最优解矛盾。
-
所以 A ∗ A^* A∗一定是原问题的最优解。


Prim算法
- 连通图的一棵生成树是包含图的所有定点的连通无环子图(一棵树)。
- 加权连通图的一棵最小生成树是图的一棵权重最小的生成树。


从某个点出发,首先找和它相邻连接的结点中,权值最小的是谁。是b结点、权值为4,那就把b结点并入进来。接着,再找下一条边,就找和a、b相邻的结点中,权值最小的是哪个边,并且把那个结点并入进来。
总之,可以视作两个集合:一个是已并入最小生成树的结点集合,另一个是还未并入的结点集合。每次找这两个集合之间权值最小的连接(不能形成环)。


问题:
一个图,按照这种方式,找出来的所有的最小生成树是不是都是一样的?
它是一棵树,树的结构是由什么决定的?——我每次的起始点选取不同,它的树根结点不一样,肯定就不一样了。


总结
贪心策略的选择很重要。
贪心在某些情况下是可以拿到最优的,但是很容易得到一个局部最优而非全局最优的解。
相关文章:

编程题四大算法思想(三)——贪心法:找零问题、背包问题、任务调度问题、活动选择问题、Prim算法
文章目录 贪心法找零问题(change-making problem)贪心算法要求基本思想适合求解问题的特征 背包问题0/1背包问题0/1背包问题——贪心法 分数背包问题 任务调度问题活动选择问题活动选择——贪心法最早结束时间优先——最优性证明 Prim算法 贪心法 我在当…...
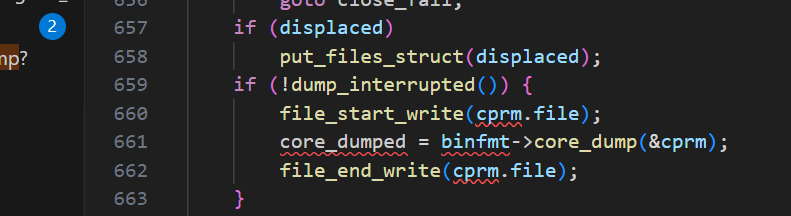
core dump管理在linux中的前世今生
目录 一、什么是core dump? 二、coredump是怎么来的? 三、怎么限制coredump文件的产生? ulimit 半永久限制 永久限制 四、从源码分析如何对coredump文件的名字和路径管理 命名 管理 一些问题的答案 1、为什么新的ubuntu不能产生c…...

Springboot整合knife4j配置swagger教程-干货
开启swagger文档,直接上教程。 第一步:引入依赖 <!--swagger 依赖--><dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-spring-boot-starter</artifactId><version>3.0.3</version></d…...

C++ 中的 Pimpl 惯用法
C 中的 Pimpl 惯用法 介绍 Pimpl(Pointer to Implementation)是一种常见的 C 设计模式,用于隐藏类的实现细节,从而减少编译依赖和提高编译速度。本文将通过一个较为复杂的例子,展示如何使用智能指针(如 s…...

【个人博客系统网站】统一处理 · 拦截器
【JavaEE】进阶 个人博客系统(2) 文章目录 【JavaEE】进阶 个人博客系统(2)1. 统一返回格式处理1.1 统一返回类common.CommonResult1.2 统一返回处理器component.ResponseAdvice 2. 统一异常处理3. 拦截器实现3.1 全局变量SESSI…...
)
深入探索PHP编程:文件操作与输入/输出(I/O)
深入探索PHP编程:文件操作与输入/输出(I/O) 在PHP编程中,文件操作和输入/输出(I/O)是不可或缺的关键部分。无论是读取、写入文件,还是处理上传的文件,这些操作都是Web开发的重要组成…...

基于jeecg-boot的flowable流程自定义业务驳回到发起人的一种处理方式
有些粉丝,希望对自定义业务中,驳回到发起人进行处理,比如可以重新进行发起流程,下面就给出一种方式,当然不一定是最好的方式,只是提供一种参考而已,以后可以考虑动态根据流程状态或节点信息进行…...

【大数据知识】大数据平台和数据中台的定义、区别以及联系
数据行业有太多数据名词,例如大数据、大数据平台、数据中台、数据仓库等等。但大家很容易混淆,也很容易产生疑问,今天我们就来简单聊聊大数据平台和数据中台的定义、区别以及联系。 大数据平台和数据中台的定义 大数据平台:一个…...

华为OD:IPv4地址转换成整数
题目描述: 存在一种虚拟IPv4地址,由4小节组成,每节的范围为0-255,以#号间隔,虚拟IPv4地址可以转换为一个32位的整数,例如: 128#0#255#255,转换为32位整数的结果为2147549183&#…...
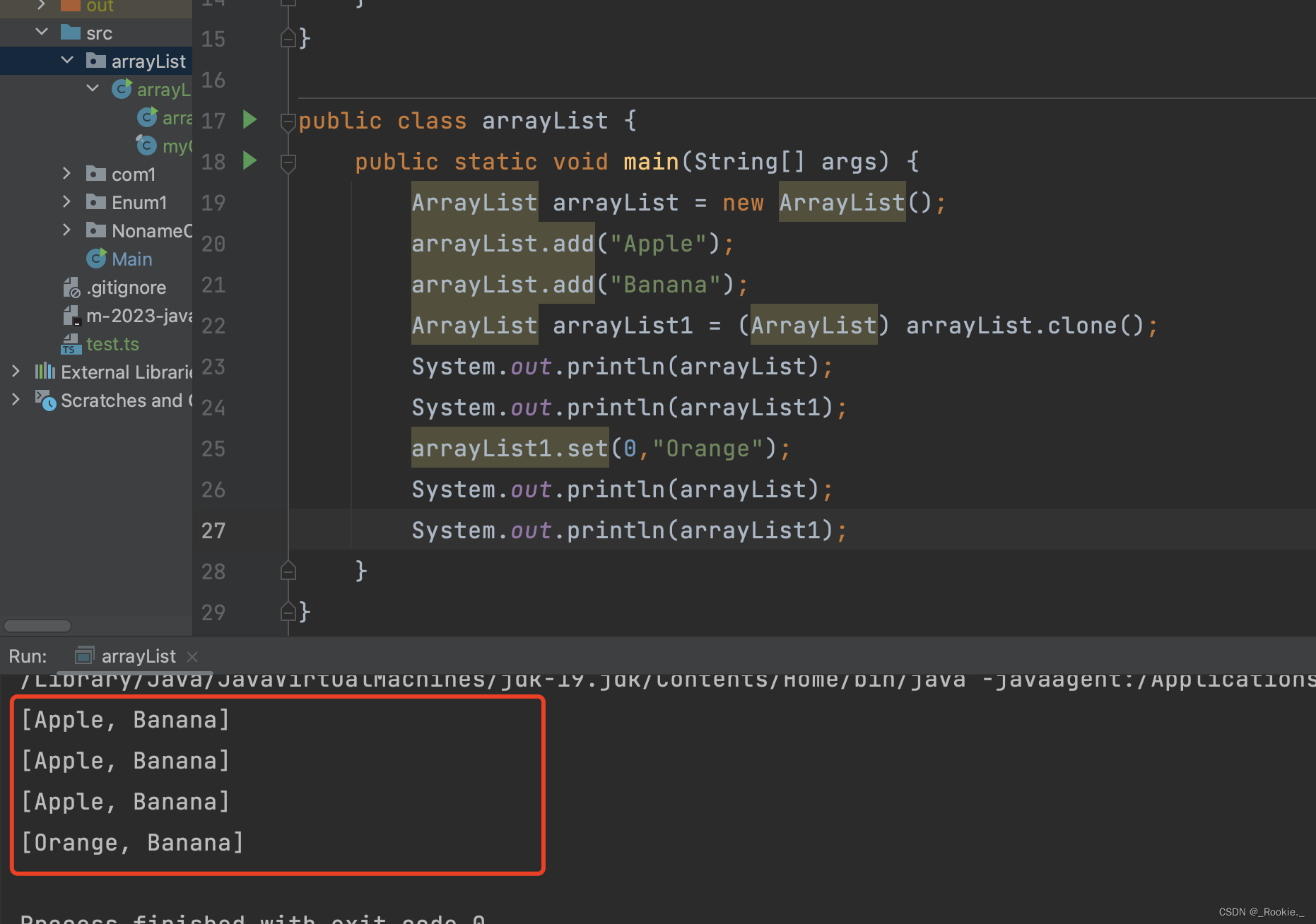
2023.9 - java - 浅拷贝
与 js的浅拷贝不同: 在 JavaScript 中, Object.assign() 或 spread 运算符等方法可以实现浅拷贝,但只针对对象的第一层属性进行复制。如果一个对象只包含基本数据类型的属性,那么对浅拷贝出来的对象进行修改不会影响原始对象&…...
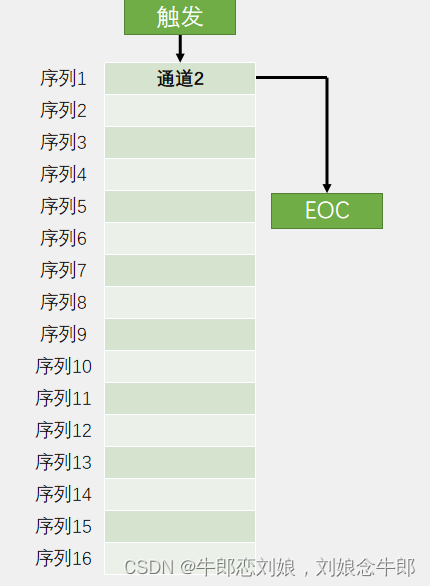
STM32f103入门(10)ADC模数转换器
ADC模数转换器 ADC简介AD单通道初始化代码编写第一步开启时钟第二步 RCCCLK分频 6分频 72M/612M第三步 配置GPIO 配置为AIN状态第四步,选择规则组的输入通道第五步 用结构体 初始化ADC第六步 对ADC进行校准编写获取电压函数初始化代码如下 Main函数编写 ADC简介 ADC…...

实训笔记8.28
实训笔记8.28 8.28笔记一、大数据计算场景主要分为两种1.1 离线计算场景1.2 实时计算场景 二、一般情况下大数据项目的开发流程2.1 数据采集存储阶段2.2 数据清洗预处理阶段2.3 数据统计分析阶段2.4 数据挖掘预测阶段2.5 数据迁移阶段2.6 数据可视化阶段 三、纯大数据离线计算项…...

机器学习笔记之最优化理论与方法(五)凸优化问题(上)
机器学习笔记之最优化理论与方法——凸优化问题[上] 引言凸优化问题的基本定义凸优化定义:示例 凸优化与非凸优化问题的区分局部最优解即全局最优解凸优化问题的最优性条件几种特殊凸问题的最优性条件无约束凸优化等式约束凸优化非负约束凸优化 引言 本节将介绍凸优…...
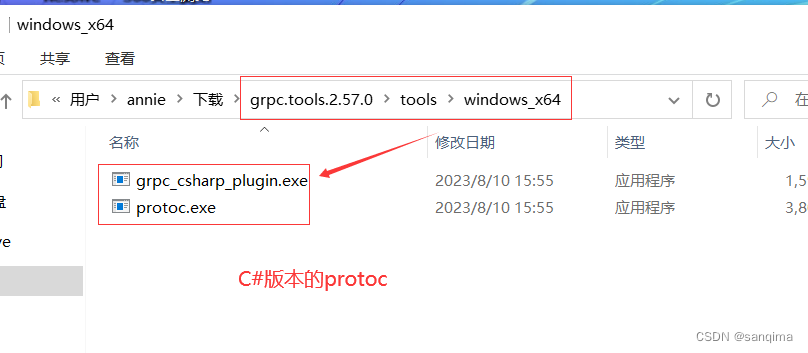
在Windows10上编译grpc工程,得到protoc.exe和grpc_cpp_plugin.exe
grpc是google于2015年发布的一款跨进程、跨语言、开源的RPC(远程过程调用)技术。使用C/S模式,在客户端、服务端共享一个protobuf二进制数据。在点对点通信、微服务、跨语言通信等领域应用很广,下面介绍grpc在windows10上编译,这里以编译grpc …...

一些测试知识
希望能起到帮助,博主主页: https://blog.csdn.net/qq_57785602/category_12023254.html?spm1001.2014.3001.5482 软件测试理论 测试的依据: 需求,规格说明,模型,用户需求等 什么是软件测试 描述一种来…...

Socket交互的基本流程?
TCP socket通信过程图 什么是网络编程,网络编程就是编写程序使两台连联网的计算机相互交换数据。怎么交换数据呢?操作系统提供了“套接字”(socket)的组件我们基于这个组件进行网络通信开发。tcp套接字工作流程都以“打电话”来生…...

css 分割线中间带文字
效果图 代码块(自适应) <div class"line"><span class"text">我是文字</span></div>.line{height:0;border-top:1px solid #000;text-align:center;}.text{position:relative;top:-14px;background-color:#…...

会不会激发对modern c++的新兴趣
可变参数好像很厉害的样子,会节省很多手写代码,让编译器自动帮我们生成代码 template<typename Fun, typename...Args> void invoke(Fun&& fun, Args&&...args) { fun(std::forward<Args>(args)...); } 任意函数包装器…...

Nginx服务器如何配合Java开发项目
Nginx服务器如何才能配合好相关的编程语言进行服务器搭建呢?下面我们就来看看有关的技术如何融合。希望大家有所收获。 在进行Nginx服务器建设的时候有很多语言的应用,其中Java 开发的web项目就是很常见的。下面我们就看看Nginx服务器如何才能与Java编程…...
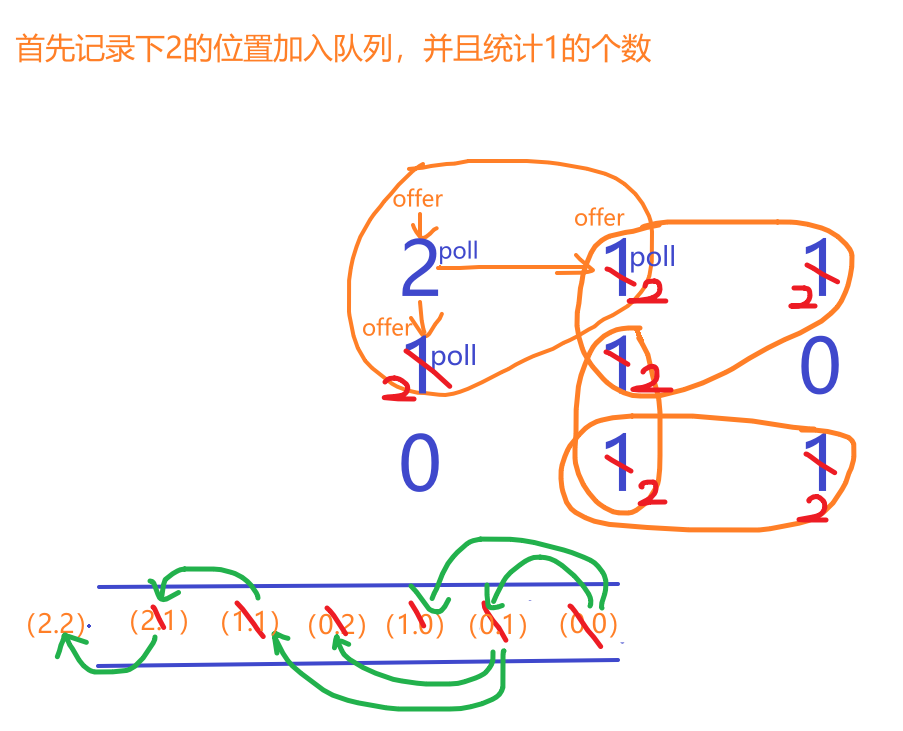
【LeetCode-中等题】994. 腐烂的橘子
文章目录 题目方法一:bfs层序遍历 题目 该题值推荐用bfs,因为是一层一层的感染,而不是一条线走到底的那种,所以深度优先搜索不适合 方法一:bfs层序遍历 广度优先搜索,就是从起点出发,每次都尝…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
