最短路Dijkstra,spfa,图论二分图算法AYIT---ACM训练(模板版)


文章目录
- 前言
- A - Dijkstra Algorithm
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- B - 最长路
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- C - 二分图最大匹配
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- D - 搭配飞行员
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- E - The Perfect Stall
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- F - Asteroids
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- G - Til the Cows Come Home
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- H - 拓扑排序
- 0x00 算法题目
- 0x01 算法思路
- 0x02 代码实现
- 总结
前言
最短路Dijkstra,spfa,图论二分图算法AYIT—ACM训练(模板版)
A — Dijkstra
B — spfa/Dijkstra
C — 二分图
D — 二分图
E — 二分图
F — 二分图
G — Dijkstra
H — Topsort
A - Dijkstra Algorithm
0x00 算法题目
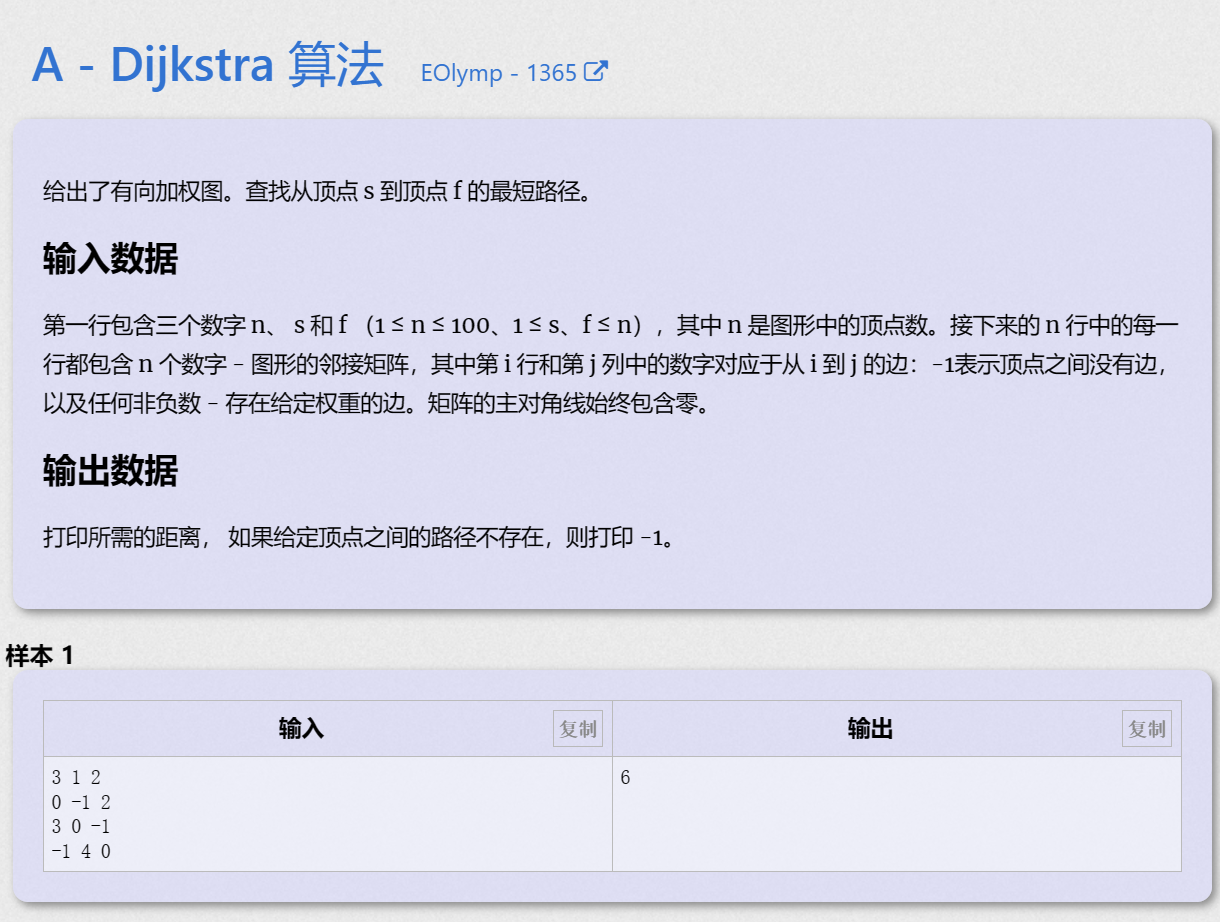
0x01 算法思路
Dijkstra算法基础模板题
💬 模板演示:
int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1]=0;for(int i=0;i<n;i++){int t=-1;for(int j=1;j<=n;j++){if(!st[j] && (t==-1 || dist[t] > dist[j]))t=j;}st[t]=true;for(int j=1;j<=n;j++)dist[j]=min(dist[j],dist[t]+g[t][j]);}if(dist[n]==0x3f3f3f3f) return -1;return dist[n];}
0x02 代码实现
朴素版本Dijkstra:
💬 代码演示:
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;
const int N = 510;
int g[N][N];
bool st[N];
int dist[N];
int n,s,f;int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[s]=0;for(int i=0;i<n;i++){int t=-1;for(int j=1;j<=n;j++)if(!st[j] && (t==-1 || dist[t] > dist[j]))t=j;st[t]=true;for(int j=1;j<=n;j++)dist[j]=min(dist[j],dist[t]+g[t][j]);}if(dist[f]==0x3f3f3f3f) return -1;return dist[f];
}int main()
{cin>>n>>s>>f;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){int x;cin>>x;if(x==-1) g[i][j]=0x3f3f3f3f;else g[i][j]=x;}}int t =dijkstra();cout<<t<<endl;return 0;
}🚩 运行结果:

spfa算法:
💬 代码演示:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>using namespace std;
const int N=110,M=110*110;
int n,s,f;
bool st[N];
int h[N],w[M],ne[M],e[M],idx;
int dist[N];void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}int spfa()
{memset(dist,0x3f,sizeof dist);dist[s]=0;queue<int> q;q.push(s);while(q.size()){int t = q.front();q.pop();st[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j] > dist[t] + w[i]){dist[j]=dist[t]+w[i];if(!st[j]){q.push(j);st[j]=true;}}}}if(dist[f]==0x3f3f3f3f) return -1;else return dist[f];
}int main()
{cin>>n>>s>>f;memset(h,-1,sizeof h);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){int x;cin>>x;//if(x==-1) continue;if(x>0) add(i,j,x);}}cout<<spfa()<<endl;return 0;
}🚩 运行结果:

B - 最长路
0x00 算法题目
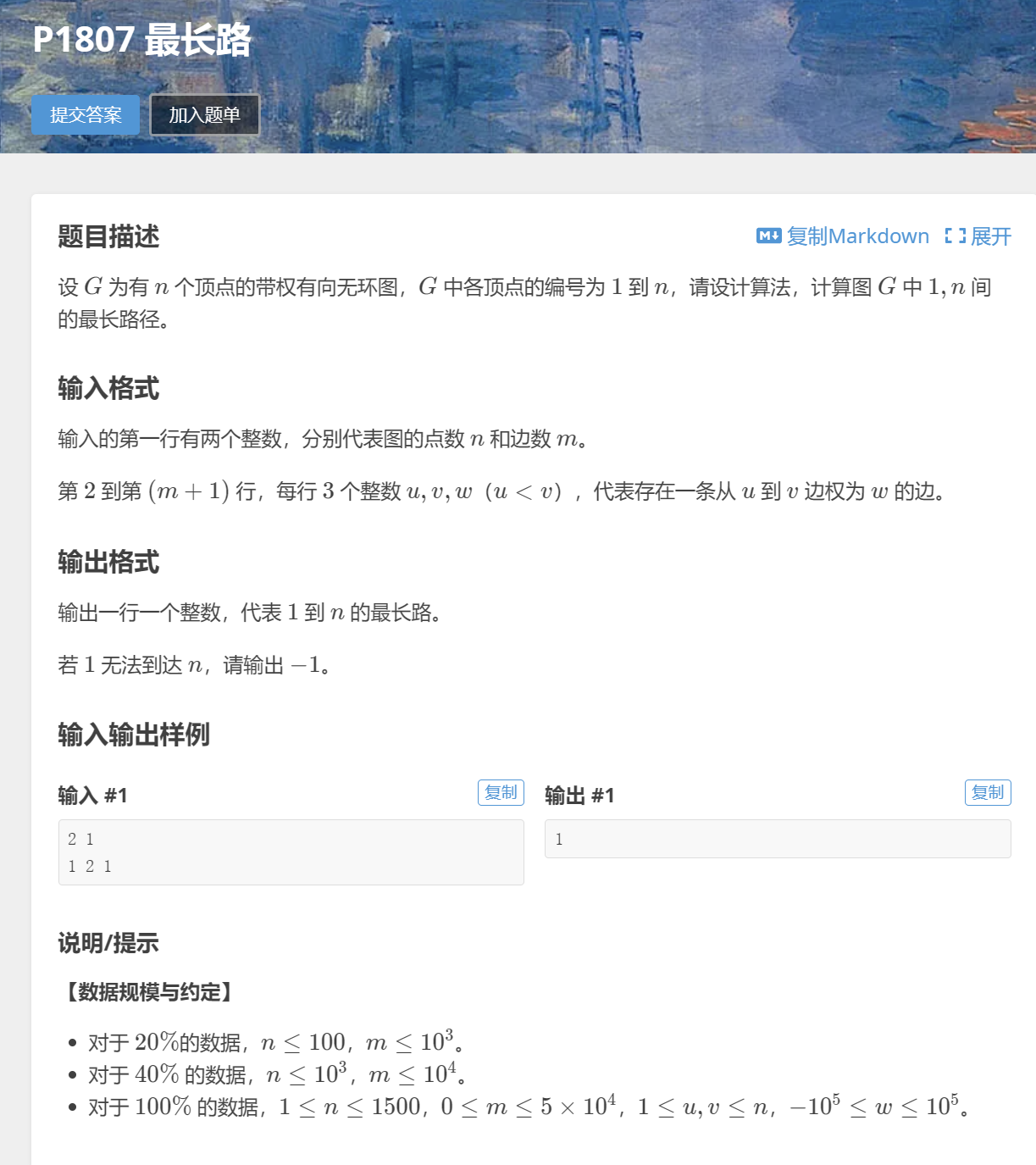
0x01 算法思路
spfa算法基础模板题
💬 模板演示:
int spfa()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;queue<int> q;q.push(1);while(q.size()){auto t = q.front();q.pop();st[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j = e[i];if(dist[j] > dist[t]+w[i]){dist[j]=dist[t]+w[i];if(!st[j]){q.push(j);st[j]=true;}}}}return dist[n];
}
0x02 代码实现
spfa算法:
💬 代码演示:
#include<bits/stdc++.h>
#define endl '\n'using namespace std;
const int N = 1510,INF = 0x3f3f3f3f;
int n,m;
int dist[N];
int g[N][N];
queue<int> q;void spfa()
{memset(dist,-1,sizeof dist);dist[1]=0;q.push(1);while(!q.empty()){int t = q.front();q.pop();for(int j=1;j<=n;j++){if(g[t][j] && dist[j] < dist[t] + g[t][j]){dist[j] = dist[t] + g[t][j];q.push(j);}}}}int main()
{cin>>n>>m;for(int i=1;i<=m;i++){int a,b,c;cin>>a>>b>>c;g[a][b]=max(g[a][b],c);}spfa();cout<<dist[n]<<endl;return 0;
}
🚩 运行结果:

C - 二分图最大匹配
0x00 算法题目
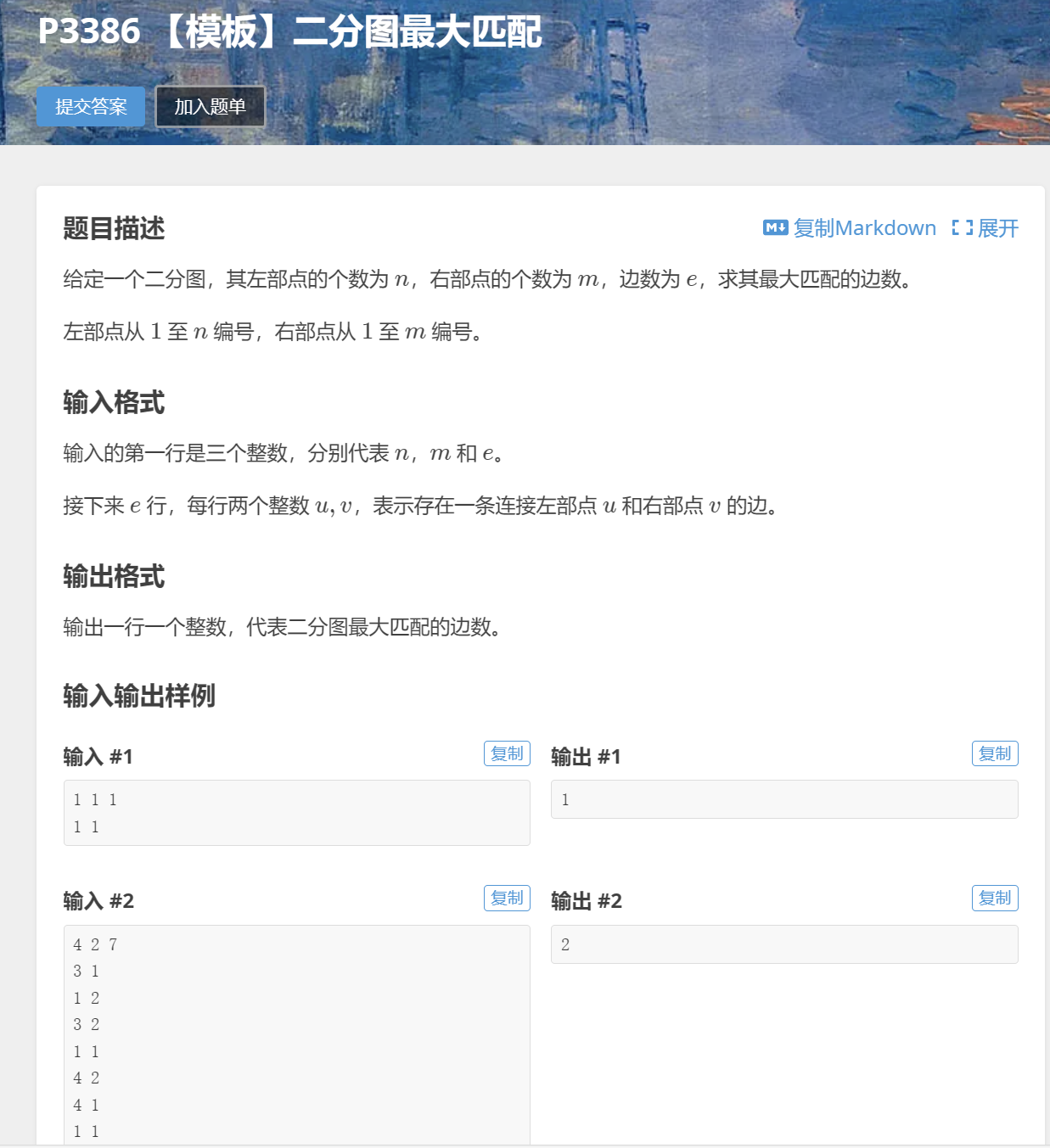
0x01 算法思路
二分图模板题
💬 模板演示:
//邻接表
bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
//邻接矩阵
bool find(int x)
{for(int i=0;i<g[x].size();++i){int j = g[x][i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}
0x02 代码实现
💬 代码演示:
#include<iostream>
#include<cstring>using namespace std;const int N = 510,M=5e4+10;
int n,m,q;
int h[N],e[M],ne[M],idx;
int match[N];
bool st[N];void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}bool find(int x)
{for(int i=h[x];i!=-1;i=ne[i]){int j = e[i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}int main()
{cin>>n>>m>>q;memset(h,-1,sizeof h);while(q--){int u,v;cin>>u>>v;add(u,v);}int res=0;for(int i=1;i<=n;i++){memset(st,false,sizeof st);if(find(i)) res++;}cout<<res<<endl;return 0;
}🚩 运行结果:

D - 搭配飞行员
0x00 算法题目

0x01 算法思路
二分图模板题
💬 模板演示:
//邻接表
bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
//邻接矩阵
bool find(int x)
{for(int i=0;i<g[x].size();++i){int j = g[x][i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}
0x02 代码实现
💬 代码演示:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<bits/stdc++.h>using namespace std;
const int N = 110;int n,m;
int map[N][N];
int match[N];
bool st[N];
vector<int> g[N];
bool find(int x)
{for(int i=0;i<g[x].size();++i){int j = g[x][i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}int main()
{scanf("%d %d",&n,&m);int a,b;while(cin>>a>>b){g[a].push_back(b);}int res = 0;for(int i=1;i<=m;i++){memset(st,false,sizeof st);if(find(i)) {res++;}}cout<<res;return 0;
}🚩 运行结果:

E - The Perfect Stall
0x00 算法题目

0x01 算法思路
二分图模板题
💬 模板演示:
//邻接表
bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
//邻接矩阵
bool find(int x)
{for(int i=0;i<g[x].size();++i){int j = g[x][i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}
0x02 代码实现
💬 代码演示:
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
const int N = 510,M=5e4+10;
int n,m;
int match[N];
bool st[N];
vector<int> g[N];bool find(int x)
{for(int i=0;i<g[x].size();++i){int j = g[x][i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}int main()
{while(~scanf("%d%d",&n,&m)){memset(st,false,sizeof st);memset(match,0,sizeof match);for(int i=1;i<=n;i++){g[i].clear();int s;cin>>s;while(s--){int q;cin>>q;g[i].push_back(q);}}int res=0;for(int i=1;i<=n;i++){memset(st,false,sizeof st);if(find(i)) res++;}cout<<res<<endl;}return 0;
}
🚩 运行结果:

F - Asteroids
0x00 算法题目

0x01 算法思路
二分图模板题
💬 模板演示:
//邻接表
bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
//邻接矩阵
bool find(int x)
{for(int i=0;i<g[x].size();++i){int j = g[x][i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}
0x02 代码实现
💬 代码演示:
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510,M=5e4+10;
int n,m,q;
int h[N],e[M],ne[M],idx;
int match[N];
bool st[N];void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}bool find(int x)
{for(int i=h[x];i!=-1;i=ne[i]){int j = e[i];if(!st[j]){st[j]=true;if(match[j]==0 || find(match[j])){match[j]=x;return true;}}}return false;
}int main()
{cin>>n>>m;memset(h,-1,sizeof h);while(m--){int u,v;cin>>u>>v;add(u,v);}int res=0;for(int i=1;i<=n;i++){memset(st,false,sizeof st);if(find(i)) res++;}cout<<res<<endl;return 0;
}🚩 运行结果:

G - Til the Cows Come Home
0x00 算法题目

0x01 算法思路
Dijkstra算法基础模板题
💬 模板演示:
int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1]=0;for(int i=0;i<n;i++){int t=-1;for(int j=1;j<=n;j++){if(!st[j] && (t==-1 || dist[t] > dist[j]))t=j;}st[t]=true;for(int j=1;j<=n;j++)dist[j]=min(dist[j],dist[t]+g[t][j]);}if(dist[n]==0x3f3f3f3f) return -1;return dist[n];}
0x02 代码实现
💬 代码演示:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<stdbool.h>using namespace std;const int N=1010,inf = 0x3f3f3f3f;int n,m;
bool st[N];
int dist[N];
int g[N][N];int dijkstra()
{memset(dist,inf,sizeof(dist));dist[1]= 0;for(int i=1;i <= n;i++){int t=-1;for(int j=1;j<=n;j++)if(!st[j] && (t==-1 || dist[t] > dist[j]))t=j;st[t]=true;for(int j=1;j<=n;j++)dist[j]=min(dist[j],dist[t]+g[t][j]);}return dist[n];
}int main()
{cin>>m>>n;memset(g,inf,sizeof g);for(int i=0;i<m;++i){int a,b,c;cin>>a>>b>>c; g[a][b]=g[b][a]=min(g[a][b],c);}cout<< dijkstra() <<endl;return 0;
}
🚩 运行结果:

H - 拓扑排序
0x00 算法题目
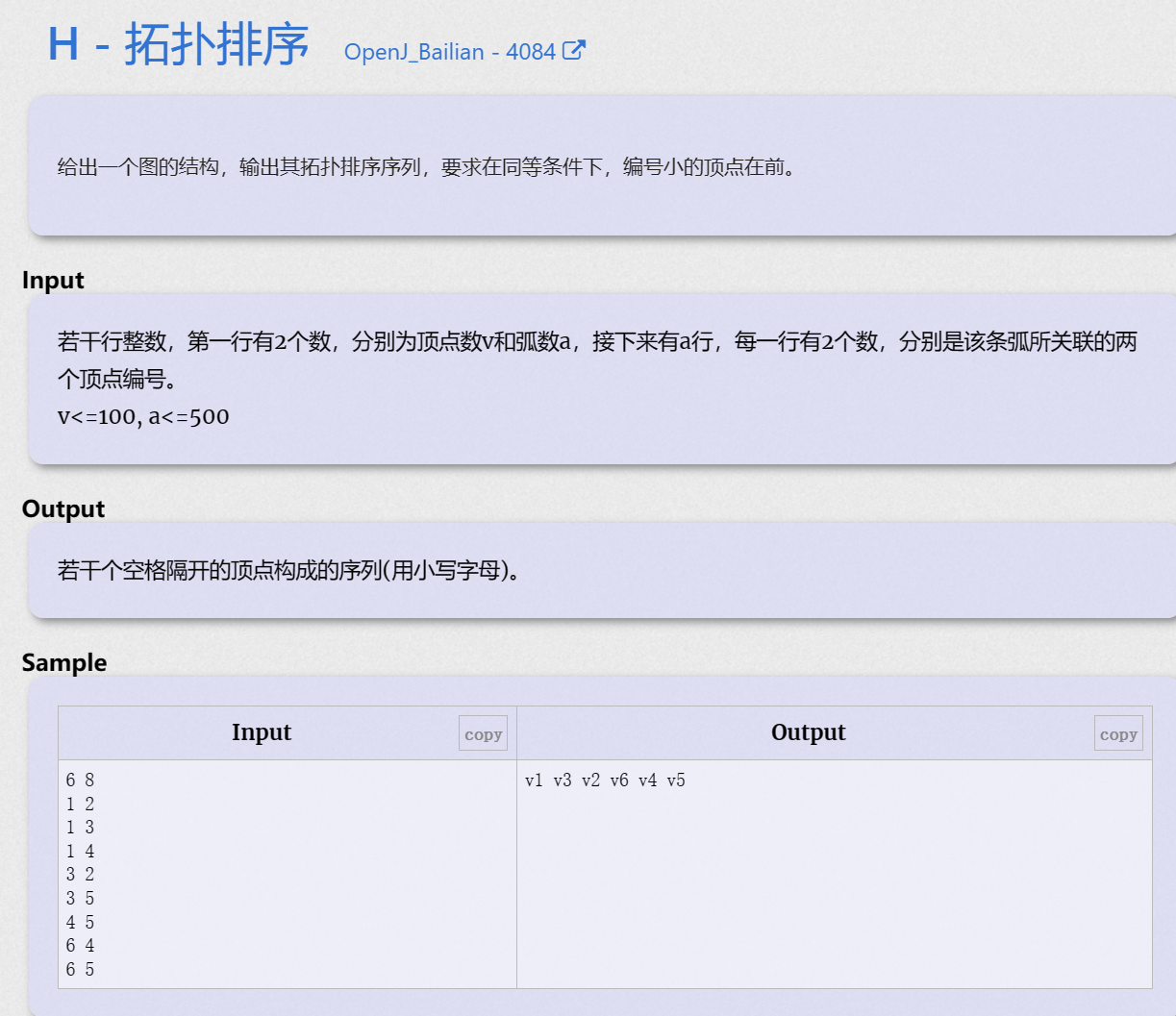
0x01 算法思路
拓扑排序算法基础模板题
💬 模板演示:
bool topsort()
{int hh=0,tt=-1;for (int i = 1; i <= n; i ++ )if (!d[i])q[ ++ tt] = i;while(hh<=tt){int t = q[hh ++ ];for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (-- d[j] == 0)q[ ++ tt] = j;}}return tt==n-1;
}
0x02 代码实现
💬 代码演示:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>using namespace std;const int N=100010;int n,m;
vector<int> v[N];
int size,d[N];
int ans[N];void topsort()
{priority_queue<int,vector<int>,greater<int> > q;for(int i=1;i<=n;i++)if(!d[i]) q.push(i);while(!q.empty()){int t = q.top();q.pop();ans[size++] = t;for(auto it : v[t]){d[it]--;if(!d[it]) q.push(it);}}
}int main()
{cin>>n>>m;for(int i=0;i<m;i++){int a,b;cin>>a>>b;v[a].push_back(b);d[b]++;}topsort();for(int i=0 ; i<size ;i++)cout<< 'v' << ans[i] <<' ';return 0;
}🚩 运行结果:

总结
这次训练很明显涉及到了最短路Dijkstra,spfa,图论二分图算法,以及topsort算法,这次考的比较基础,但是让我意识到了,算法必须熟练记忆模板是很重要的。
相关文章:

最短路Dijkstra,spfa,图论二分图算法AYIT---ACM训练(模板版)
文章目录 前言A - Dijkstra Algorithm0x00 算法题目0x01 算法思路0x02 代码实现 B - 最长路0x00 算法题目0x01 算法思路0x02 代码实现 C - 二分图最大匹配0x00 算法题目0x01 算法思路0x02 代码实现 D - 搭配飞行员0x00 算法题目0x01 算法思路0x02 代码实现 E - The Perfect Sta…...

AK 微众银行 9.3 笔试 Java后端方向
T1(模拟,二分) (没看清买的糖果只有前缀,一开始用二分写了,后来意识到也没改了,简单写的话,直接模拟就好了) #include <bits/stdc.h>#define endl \nusing namespace std;const int N 50010;int n; int a[N];bool check(…...
了解java中的通配符“?“
目录 通配符的作用 先看一段代码 用通配符"?"后,代码变化 结论 通配符上界 通配符下界 对通配符上下界的注释理解及其练习代码 简记: ? 用于在泛型的使用,即为通配符. 在Java中,通配符(wildcard)主要用于泛型…...

浙大陈越何钦铭数据结构07-图6 旅游规划【最小堆实现】
题目: 题目和浙大陈越何钦铭数据结构07-图6 旅游规划是一样的,不同的是用最小堆实现函数【FindMinDist】。 时间复杂度对比: 浙大陈越何钦铭数据结构07-图6 旅游规划: 创建图(CreateGraph):时…...
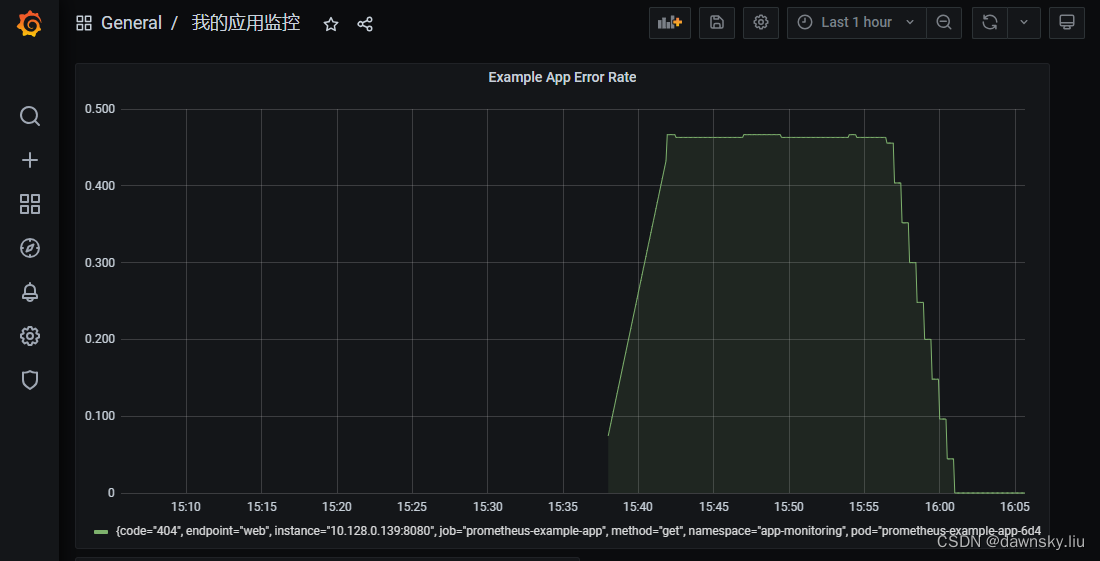
OpenShift 4 - 用 Prometheus 和 Grafana 监视用户应用定制的观测指标(视频)
《OpenShift / RHEL / DevSecOps 汇总目录》 说明:本文已经在 OpenShift 4.13 的环境中验证 文章目录 OpenShift 的监控功能构成部署被监控应用用 OpenShift 内置功能监控应用用 Grafana 监控应用安装 Grafana 运行环境配置 Grafana 数据源定制监控 Dashboard 演示视…...
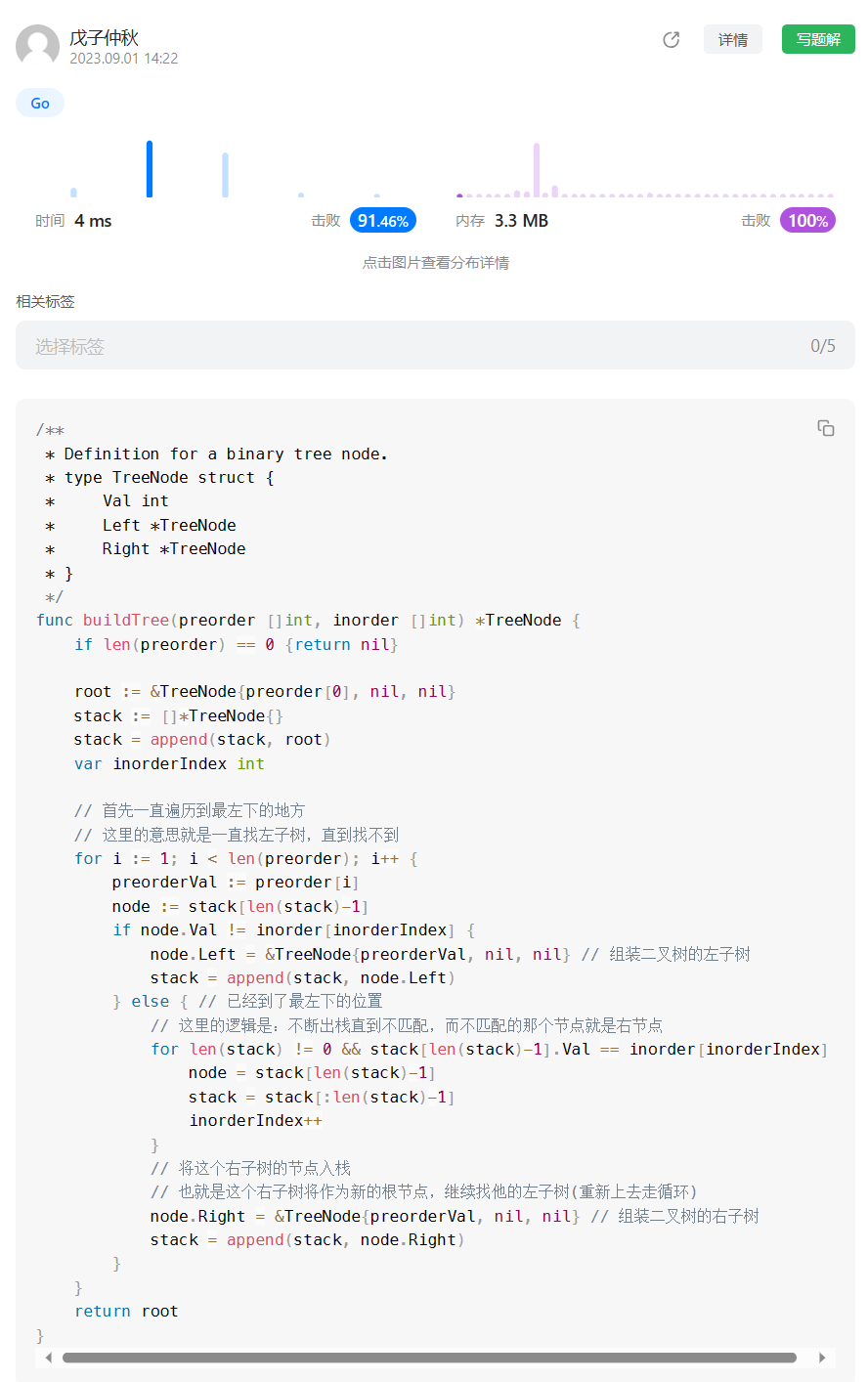
【LeetCode】剑指 Offer <二刷>(3)
目录 题目:剑指 Offer 06. 从尾到头打印链表 - 力扣(LeetCode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 07. 重建二叉树 - 力扣…...

Ceph IO流程及数据分布
1. Ceph IO流程及数据分布 1.1 正常IO流程图 步骤: client 创建cluster handler。client 读取配置文件。client 连接上monitor,获取集群map信息。client 读写io 根据crshmap 算法请求对应的主osd数据节点。主osd数据节点同时写入另外两个副本节点数据。…...

Netty-NIO
文章目录 一、NIO-Selector1.处理accept2.cancel3.处理read4.处理客户端断开5. 处理消息的边界6. 写入内容过多的问题7. 处理可写事件 一、NIO-Selector 1.处理accept //1.创建selector,管理多个channel Selector selector Selector.open(); ByteBuffer buffer ByteBuffer.…...

红外物理学习笔记 ——第三章
第三章 基尔霍夫定律:就是说物体热平衡条件下,发射的辐射功率要等于吸收的辐射功率 M α E M\alpha E MαE α \alpha α 是吸收率, M M M 是幅出度(发射出去的), E E E是辐照度(外面照过来的…...

使用 htmx 构建交互式 Web 应用
学习目标:了解htmx的基本概念、特点和用法,并能够运用htmx来创建交互式的Web应用程序。 学习内容: 1. 什么是htmx? - htmx是一种用于构建交互式Web应用程序的JavaScript库。 - 它通过将HTML扩展为一种声明性的交互式语言&a…...
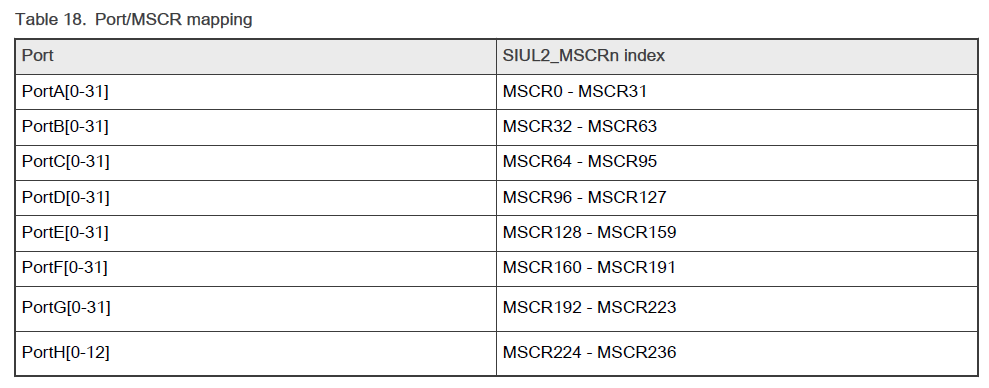
S32K324芯片学习笔记
文章目录 Core and architectureDMASystem and power managementMemory and memory interfacesClocksSecurity and integrity安全与完整性Safety ISO26262Analog、Timers功能框图内存mapflash Signal MultiplexingPort和MSCR寄存器的mapping Core and architecture 两个Arm Co…...

htmx-使HTML更强大
本文作者是360奇舞团开发工程师 htmx 让我们先来看一段俳句: javascript fatigue: longing for a hypertext already in hand 这个俳句很有意思,是开源项目htmx文档中写的,意思是说,我们已经有了超文本,为什么还要去使用javascr…...
Java学习之序列化
1、引言 《手册》第 9 页 “OOP 规约” 部分有一段关于序列化的约定 1: 【强制】当序列化类新增属性时,请不要修改 serialVersionUID 字段,以避免反序列失败;如果完全不兼容升级,避免反序列化混乱,那么请…...
C++实现蜂群涌现效果(flocking)
Flocking算法0704_元宇宙中的程序员的博客-CSDN博客 每个个体的位置,通过计算与周围个体的速度、角度、位置,去更新位置。...
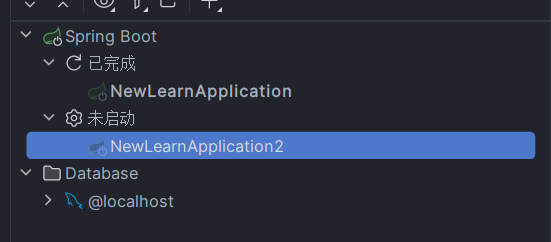
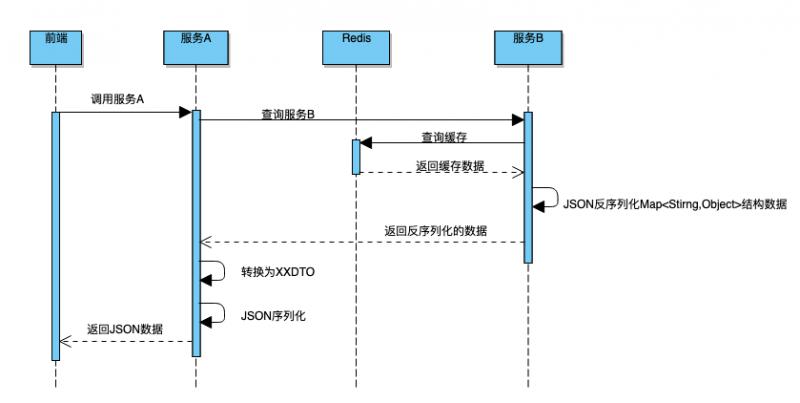
IDEA复制一个工程为多个并启动,测试负载均衡
1 找到服务按钮 2 选择复制配置 3 更改新的名称与虚拟机参数 复制下面的代码在VM参数中 -Dserver.port8082 4 最后启动即可...

001_C++语法基础
C语法基础 所有C语法要用英文区分大小写每个语句写完以分号结束 C标准输入输出头文件iostream 若想通过C实现数据的输入和输出,需要导入标准输入输出头文件 #include <iostream>标准输入输出头文件<iostream>中包含了cin输入语句和cout输出语句 标…...
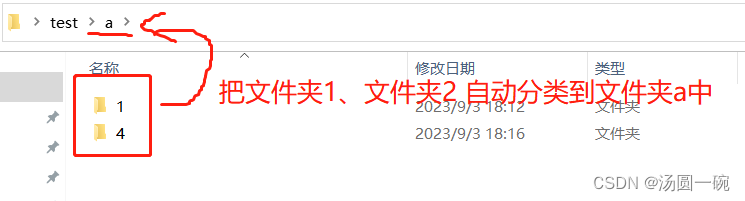
对Excel表中归类的文件夹进行自动分类
首先把excel表另存为.txt文件(注意:刚开始可能是ANSI格式,需要转成UTF-8格式);再新建一个.txt文件,重命名成.bat文件(注意:直接创建的如果是是UTF-8格式,最好转成ANSI格式࿰…...
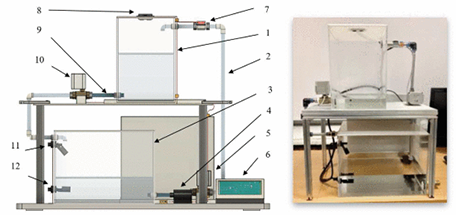
LabVIEW液压支架控制系统的使用与各种配置的预测模型的比较分析
LabVIEW液压支架控制系统的使用与各种配置的预测模型的比较分析 模型预测控制在工业中应用广泛。这种方法的优点之一是在求解最优控制问题时能够明确考虑对输入和输出状态施加的约束。控制对象模型用于有限时间范围内最优控制的实时计算。所使用的数学设备允许从具有单输入和单…...

C++中位运算符使用
& 与 只有都为1结果为1 0 & 0 00 & 1 01 & 0 01 & 1 1 | 或 只要一个为1结果为1 0|00 0|11 1|01 1|11 ^ 异或 两个相同的数字为0,其余为1 0^00 1^01 0^11 1^10 ~ 取反 将进制位数进行取反 ~1-2 //0000 0001-->代…...

微机原理 || 第2次测试:汇编指令(加减乘除运算,XOR,PUSH,POP,寻址方式,物理地址公式,状态标志位)(测试题+手写解析)
(一)测试题目: 1.数[X]补1111,1110B,则其真值为 2.在I/O指令中,可用于表示端口地址的寄存器 3. MOV AX,[BXSl]的指令中,源操作数的物理地址应该如何计算 4.执行以下两条指令后,标志寄存器FLAGS的六个状态…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
