动态规划:路径和子数组问题(C++)
动态规划:路径和子数组问题
- 路径问题
- 1.不同路径(中等)
- 2.不同路径II(中等)
- 3.下降路径最⼩和(中等)
- 4.地下城游戏(困难)
- 子数组问题
- 1.最大子数组和(中等)
- 2.环形子数组的最大和(中等)
- 3.乘积最大子数组(中等)
- 4.乘积为正数的最长子数组(中等)
- 5.等差数列划分(中等)
- 6.最长湍流子数组(中等)
- 7.单词拆分(中等)
- 8.环绕字符串中唯⼀的子字符串(中等)
路径问题
1.不同路径(中等)
链接:不同路径
-
题目描述
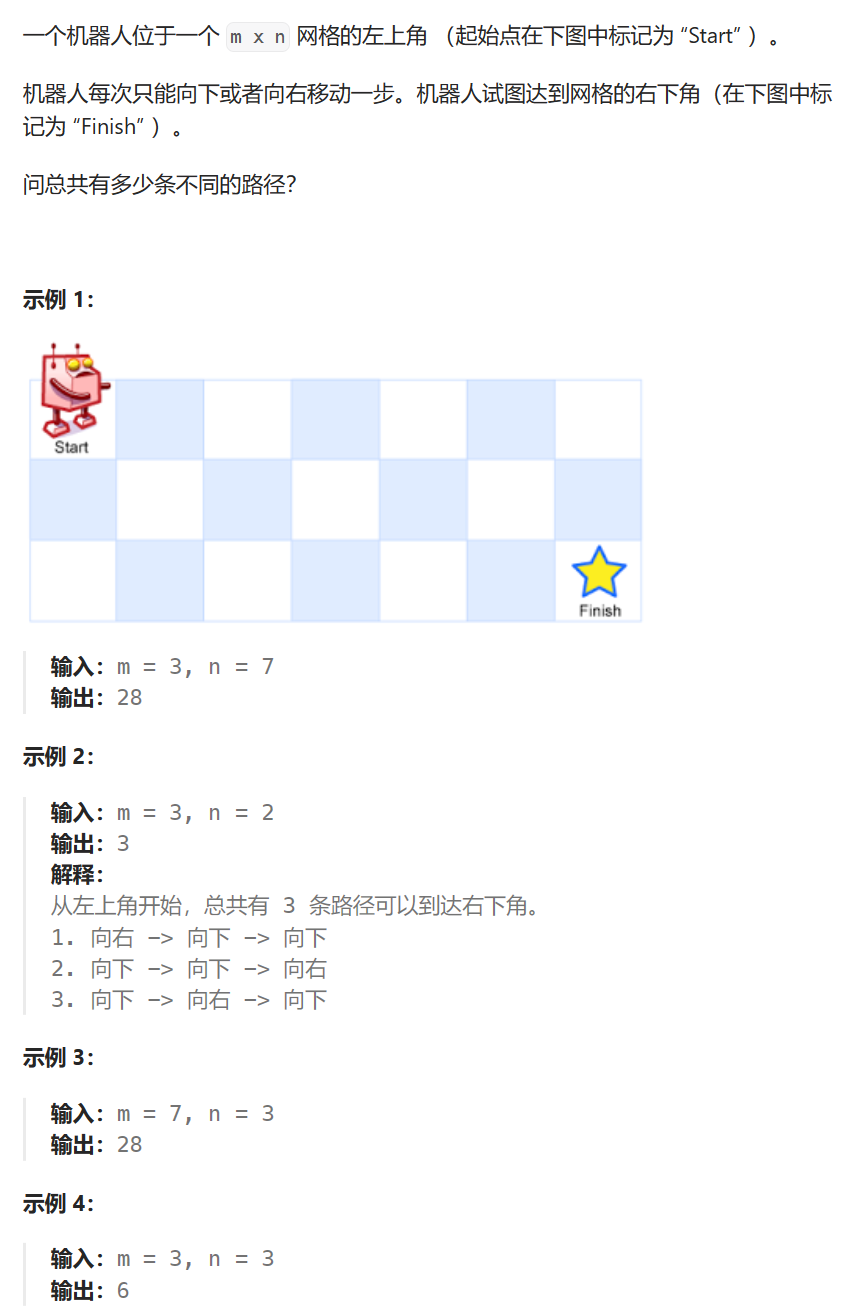
-
做题步骤
-
状态表示
尝试定义状态表示为到达[m, n]位置的路径数。

-
状态转移方程
通过上述分析,可知状态转移方程为:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。 -
初始化

-
填表顺序
保证填当前状态时,所需状态已经计算过,从起点出发,填表顺序为从上往下,每一行从左往右。 -
返回值
根据状态表示,返回的应该是dp[m][n],即到达终点的路径数。
- 代码实现
class Solution {
public:int uniquePaths(int m, int n) {//dp[i][j]表示到达该位置的路径vector<vector<int>> dp(m+1, vector<int>(n+1,0));dp[0][1] = 1;for(int i = 1; i <= m; i++){for(int j = 1; j <= n;j++){dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}} return dp[m][n];//时间复杂度:O(N)//空间复杂度:O(N^M)}
};//滚动数组优化
// class Solution {
// public:
// int uniquePaths(int m, int n)
// {
// vector<int> dp(n + 1);
// dp[1] = 1;// for(int i = 1; i <= m; i++)
// {
// for(int j = 1; j <= n;j++)
// {
// dp[j] += dp[j-1];
// }
// }
// return dp[n];
// }
// };
2.不同路径II(中等)
链接:不同路径II
-
题目描述
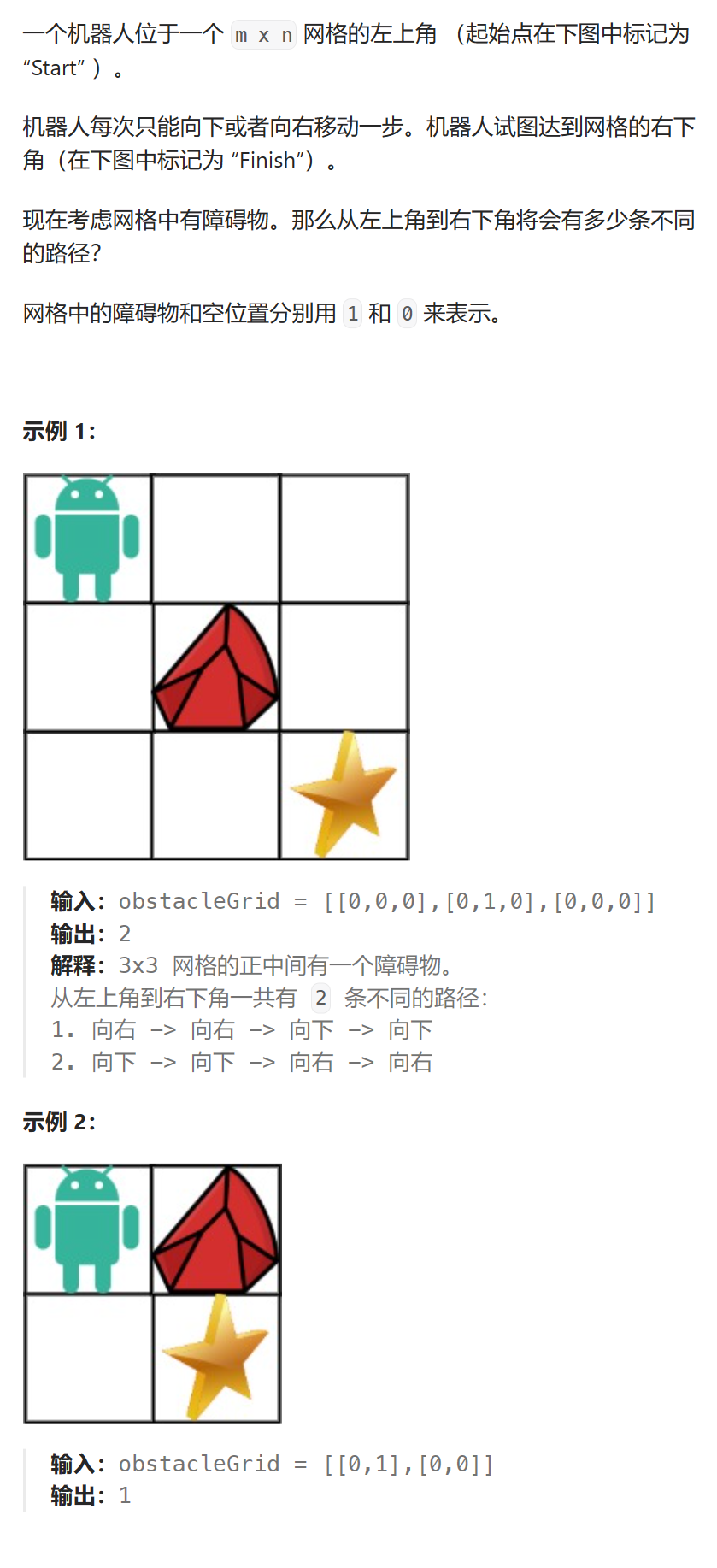
-
做题步骤
-
状态表示
这个题和第一题唯一不同就是加入了障碍物(1),我们只需要进行判断,如果该位置是障碍物就填0,否则依据转移方程填表。 -
状态转移方程
通过上述分析,可知状态转移方程为:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。 -
初始化
和第一题一样,多开一圈,dp[0][1]或dp[1][0]初始为1。 -
填表顺序
和第一题一样,填表顺序为从上往下,每一行从左往右。 -
返回值
根据状态表示,返回的应该是dp[m][n],即到达终点的路径数。
- 代码实现
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();//dp[i][j]:到达该位置的路径数vector<vector<int>> dp(m + 1,vector<int>(n + 1));dp[0][1] = 1; //dp[1][0] = 1;for(int i = 1; i < m + 1; i++){for(int j = 1; j < n + 1; j++){//多开了一圈,注意下标映射if(obstacleGrid[i - 1][j - 1] == 0){dp[i][j] = dp[i-1][j] + dp[i][j-1];}//vector默认初始0,障碍物对应位置无需处理}}return dp[m][n];//时间复杂度:O(N)//空间复杂度:O(N^2)}
};
3.下降路径最⼩和(中等)
链接:下降路径最⼩和
-
题目描述
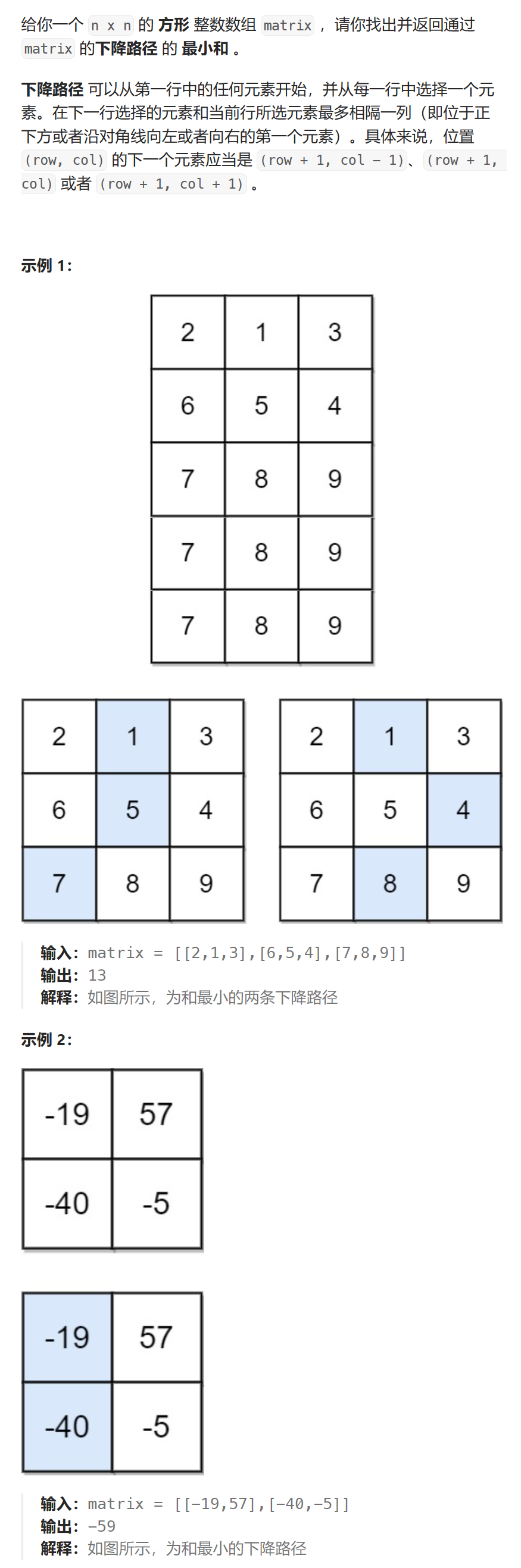
-
做题步骤
-
状态表示
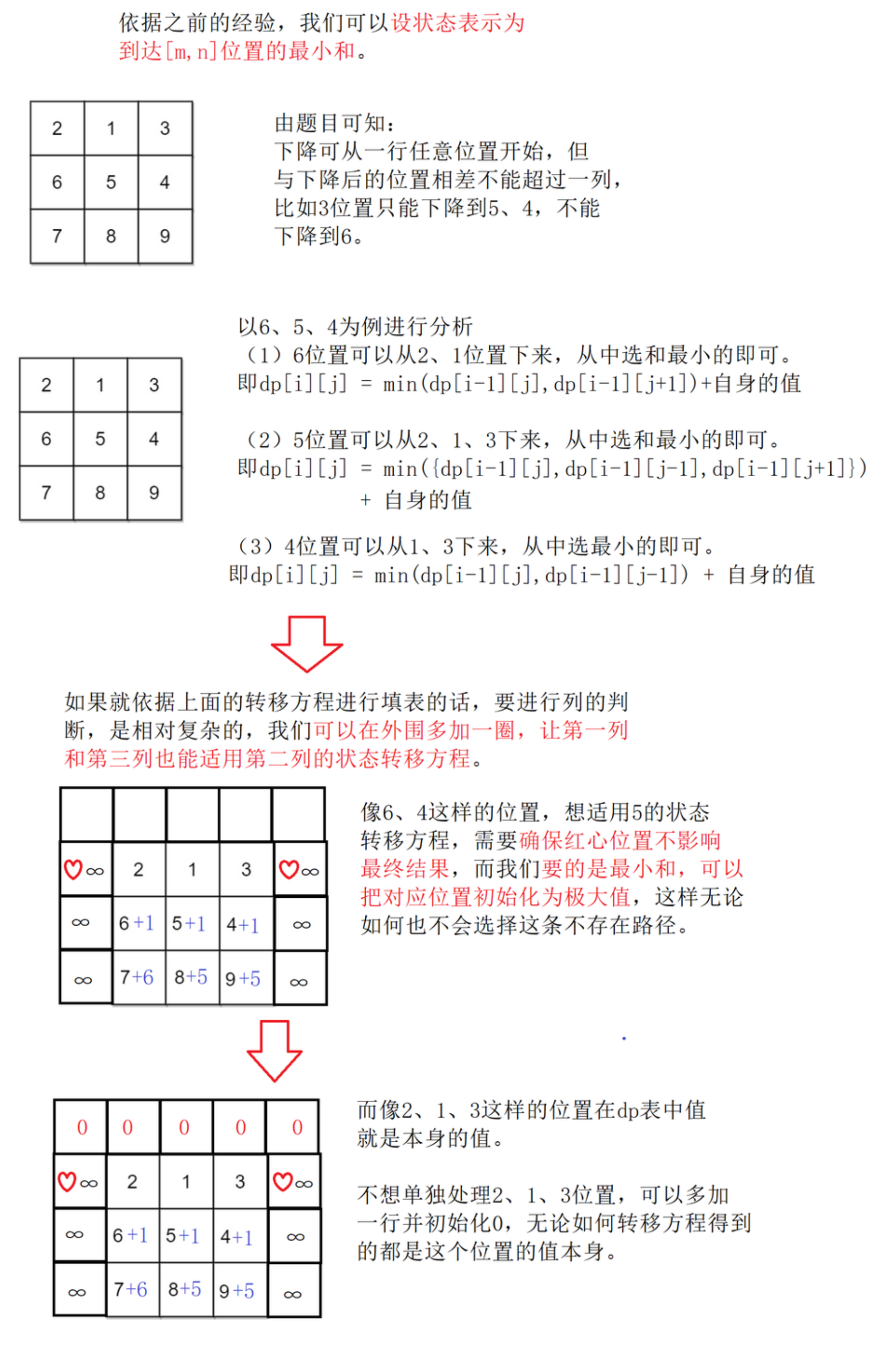
-
状态转移方程
由前面的分析可知,状态转移方程为:
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i - 1][j + 1]}) + matrix[i - 1][j - 1](本身的值) -
初始化
先全部初始化为极大值,然后第一行初始化为0。 -
填表顺序
从上往下,每一行从左往右。 -
返回值
依据状态表示和题目要求,返回最后一行的最小值即可。
- 代码实现
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {//dp[i][j]表示到这个位置最小路径和int n = matrix.size();vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));//初始化第一行for(int j = 0; j < n + 2; j++){dp[0][j] = 0;}for(int i = 1; i < n + 1; i++){for(int j = 1; j < n + 1; j++){dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]})+ matrix[i - 1][j - 1]; }}//再遍历一次找最小int ret = dp[n][0];for(auto e : dp[n]){ret = min(ret, e); }return ret;//时间复杂度:O(N)//空间复杂度:O(N^2)}
};
4.地下城游戏(困难)
链接:地下城游戏
- 题目描述

- 做题步骤
- 状态表示
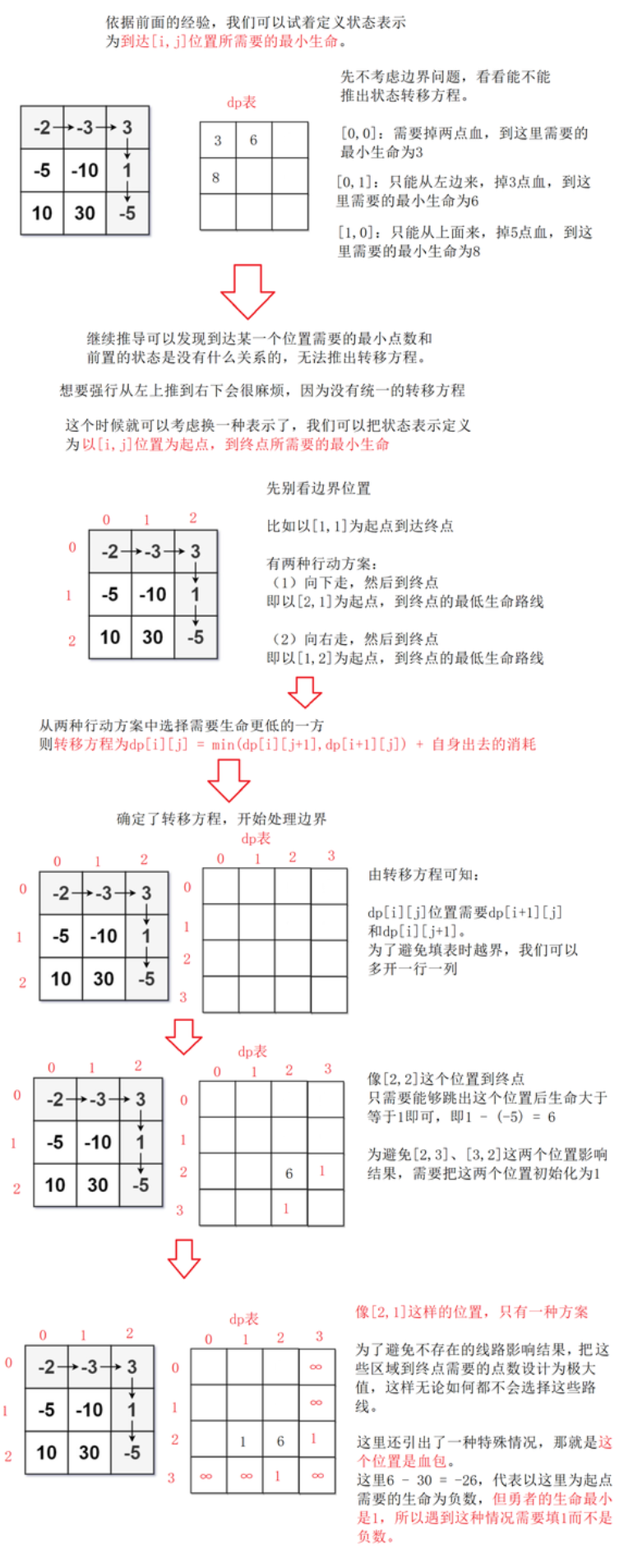
-
状态转移方程
由前面的分析可知,状态转移方程为:
dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j](自身出去的消耗) -
初始化
先将所有值初始化为极大值,dp[m][n - 1] = dp[m - 1][n] = 1。 -
填表顺序
从下往上,每一行从右向左。 -
返回值
由状态表示可知,返回值为dp[0][0](即[0,0]位置到终点需要的最小生命)
- 代码实现
// 看点位的状态表示
//从左上到右下:点位表示到这里需要的最小健康点数,点位并不是只受到左边和上面的影响,也要受后面点位的影响(后面点位可能使自己死亡),这种状态表示肯定不能//从右下到左上:点位表示从这里开始到终点所需要的最小健康点数。class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {//dp[i][j]表示以这个位置为起点到终点所需要的最小健康点数int m = dungeon.size();int n = dungeon[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));//初始化dp[m][n - 1] = dp[m - 1][n] = 1;for(int i = m - 1; i >= 0; i--){for(int j = n - 1; j >=0; j--){dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j];//如果dp[i][j]为负数,说明这个位置是奶//直接奶满了,从这里到终点所要的点数1就足够(小于1就死了)dp[i][j] = max(dp[i][j], 1);}}return dp[0][0];//时间复杂度:O(N)//空间复杂度:O(N^2)}
};
子数组问题
1.最大子数组和(中等)
链接:最大子数组和
- 题目描述

- 做题步骤
-
状态表示
这个题目我们可以定义状态表示为以i位置为结尾的子数组的最大和。
因为子数组必须是连续的,所以i位置有两种选择:
(1)接在以i - 1位置为结尾的子数组后面,即dp[i] = dp[i - 1] + 自身点数
(2)不接在别人后面(可能dp[i - 1]是负值),就自己一个,即dp[i] = 自身点数
从两种选择中选择最大的一种,即dp[i] = max(dp[i -1] + 自身点数, 自身点数) -
状态转移方程
由前面的分析可知,状态转移方程为:
dp[i] = max(dp[i -1] + 自身点数, 自身点数) -
初始化
无需初始化。 -
填表顺序
从左往右。 -
返回值
无法直接确定最大子数组的结尾位置,可以定义变量ret,一边dp一边更新最大值。
- 代码实现
class Solution {
public:int maxSubArray(vector<int>& nums) {//在原数组上面dp就行//dp[i]:以i位置为结尾的最大子数组和int ret = nums[0];for(int i = 1; i < nums.size(); i++){nums[i] = max(nums[i - 1] + nums[i], nums[i]);//遍历的过程顺便找最大ret = max(ret, nums[i]); } return ret;//时间复杂度:O(N)//空间复杂度:O(1)}
};
2.环形子数组的最大和(中等)
链接:环形子数组的最大和
-
题目描述

-
做题步骤
-
状态表示
这个题目和前一题类似,我们依然可以定义状态表示为以i位置为结尾的最大子数组和。
对于环形问题,最常见的做法就是分情况讨论,分解问题:
(1)最大子数组不成环,比如[-1,2,3,-1],这个情况做法和前一道题一样。
(2)最大子数组成环,比如[2,1,-3,-2,1],最大子数组成环情况,数组中剩余的连续部分一定是最小子数组。
子数组是连续的,环形可以理解为左右扩张,所有有利于自己的连续部分一定会被吞并,剩下的一定是最小子数组和。
但数组的总和是不变的,我们只需要用总和减去最小子数组和即可得到成环情况的最大和。 -
状态转移方程
不成环最大子数组和用f表来记录,最小子数组和用g表来记录
状态转移方程为:
f[i] = max(nums[i], f[i - 1] + nums[i])
g[i] = min(nums[i], g[i - 1] + nums[i]) -
初始化
为避免填表越界,处理第一个位置,f[0] = g[0] = nums[0] -
填表顺序
都是从左往右。 -
返回值
无法直接确定最大(小)子数组的结尾,所以一边dp一边记录最大(小)值。
(1)f表最大值->fmax
(2)g表最小值->gmin
(3)总和->sum
还有一种特殊情况就是环形数组长度为0(数组中全是负数),这个时候最大值为fmax而不是0,所以返回值为sum == gmin ? fmax : max(fmax, sum - gmin)。
- 代码实现
class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n = nums.size();//一种情况是不需要环形,区间就在数组中//第二种情况是需要环形,数组总大小恒定//非目标区间是连续并且在数组中的,所以最大 = 总 - 非目标区间//比如 5 -3 5,第一种得到5,第二种为 7(总) - (-3) = 10int sum = nums[0];//f[i]:以i位置为结尾的不成环最大子数组和vector<int> f(n);//g[i]:以i位置为结尾的最小子数组和auto g = f;f[0] = g[0] = nums[0];int fmax = nums[0];int gmin = nums[0];for(int i = 1; i < n; i++){f[i] = max(nums[i], f[i - 1] + nums[i]);g[i] = min(nums[i], g[i - 1] + nums[i]);fmax = max(fmax, f[i]);gmin = min(gmin, g[i]);sum += nums[i];}//sum和gmin相同说明里面全是负数,这个时候fmax才是最大,不能为0return sum == gmin ? fmax : max(fmax, sum - gmin);//时间复杂度:O(N)//空间复杂度:O(N)}
};
3.乘积最大子数组(中等)
链接:乘积最大子数组
-
题目描述

-
做题步骤
这个题目子数组长度最小可以为1,其实所有子数组默认乘了一个1。
-
状态表示
依据前面最大子数组和的经验,我们可以定义状态为以i位置为结尾的最大乘积。
但只有这一个状态表示是不够的,负数的加入对乘积影响是巨大的,比如[1,2,3,-1,-2,1],前面按最大和的做法来还没问题,但遇到多个负数就会出问题,这里[1,2,3,-1,-2]可以得到最大乘积12,如果按照最大和的做法只能得到6。
出现上面情况的原因在于负数的出现使得原来的最大乘积变成了最小乘积,但如果保存最小乘积,当遇到负数时最小乘积就可以变成最大乘积。
综上所述,我们需要同时记录最大和最小乘积,其中最大用f表记录,最小用g表记录。
(1)x = nums[i](当前位置的值)
(2)y = f[i - 1](前一个位置的最大乘积)
(3)z = g[i - 1](前一个位置的最小乘积) -
状态转移方程
一共就三种情况:
(1)x:不接在别人后面,子数组长度为1。
(2)x * y:接在前一个位置最大乘积子数组后面,有可能得到最大(小)乘积。
(3)y * z:接在前一个位置最小乘积子数组后面,有可能得到最大(小)乘积。
由此可知状态转移方程为:
f[i] = max( {x, x * y, x * z} )
g[i] = min( {x, x * y, x * z} ) -
初始化
当前位置的f、g更新需要前一个位置,第一个位置的最大(小)乘积就是值本身,为了避免第一个位置越界,可以在前面多开一个空间并初始化为1,即f[0] = g[0] = 1,这样不会影响第一个位置。 -
填表顺序
从左往右。 -
返回值
无法直接确定最大子数组的结尾位置,一边dp一边更新最大值。
- 代码实现
class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();//dp[i]:以i为结尾的最大乘积//f[i]表示最大乘积,g[i]表示最小乘积vector<int> f(n + 1);auto g = f;f[0] = g[0] = 1;//ret变量记录最大乘积int ret = INT_MIN;for(int i = 1; i <= n; i++){int x = nums[i - 1];//现在int y = f[i - 1]; //上个位置的最大乘积int z = g[i - 1]; //上个位置的最小乘积//如果遇到负数的情况,原本最大乘积可能会变成最小,原本最小可能会变成最大f[i] = max({x, x * y, x * z});g[i] = min({x, x * y, x * z});ret = max(ret, f[i]);}return ret;//时间复杂度:O(N)//空间复杂度:O(N)}
};
4.乘积为正数的最长子数组(中等)
链接:乘积为正数的最长子数组
-
题目描述

-
做题步骤
-
状态表示
这个题目和上一道类似,要考虑负数的加入,因此只有一个状态表示是不够的。
(1)f表:以i位置为结尾,乘积为正数的最长子数组长度。
(2)g表:以i位置为结尾,乘积为负数的最长子数组长度。 -
状态转移方程
设当前位置的值为x
(1)x为负数时,接在前一个位置的后面,原本乘积正数的子数组会变成负数,乘积负数的子数组会变成正数。
即f[i] = g[i - 1] + 1 和 g[i] = f[i - 1] + 1,但前一个位置结尾的子数组乘积可能无法出现负数(前面都是正数),即g[i - 1] == 0,这个时候f[i]应该也为0。
故状态转移方程为:
f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1
g[i] = f[i - 1] + 1
(2)当x为正数时,接在前一个位置的后面,原本乘积正数的子数组还是正数,乘积负数的子数组还是负数。
(也要考虑前一个位置乘积负数不存在的情况)
故状态转移方程为:
f[i] = f[i - 1] + 1
g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1 -
初始化
当前位置的f、g更新需要前一个位置,第一个位置为负数,g[i]为1,f[i]为0,值为正数则相反。为了避免第一个位置越界,可以在前面多开一个空间并初始化为0,即f[0] = g[0] = 0,这样不会影响第一个位置。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序很明显是从左往右 -
返回值
无法直接确定乘积为正数的最长子数组结尾位置,定义变量ret,一边dp一边更新最大值。
- 代码实现
class Solution {
public:int getMaxLen(vector<int>& nums) {//dp[i] 表示这个位置乘积为负数/正数时的最大长度int n = nums.size();vector<int> f(n + 1); // 正数auto g = f;//负数int ret = -1;for(int i = 1; i < n + 1; i++){//这个数是正数if(nums[i - 1] > 0){f[i] = f[i - 1] + 1;//要考虑前一个位置乘积负数不存在的情况g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1; }else if(nums[i - 1] < 0) //负数{f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1; }//这个数为0,两个状态都不存在,不用处理(本来就是0)ret = max(ret, f[i]);}return ret;//时间复杂度:O(N)//空间复杂度:O(N)}
};
5.等差数列划分(中等)
链接:等差数列划分
- 题目描述

- 做题步骤
-
状态表示
依据前面的经验,我们可以定义状态表示为以i位置为结尾的等差数组个数。 -
状态转移方程
以[1,2,3,4]为例子进行分析:
(1)像1、2这样的位置为结尾数组长度不足3,是一定不能构成等差数组的,即dp[i] = 0。
(2)像4这样的位置,先看能不能和前面两个元素构成等差数组(满足nums[i] + nums[i - 2] == 2* nums[i - 1]),如果可以的话那4也一定可以接在以3为结尾的等差数组后面,即dp[i] = dp[i - 1] + 1。
综上所述,状态转移方程为:
可以和前两个数构成等差数组:dp[i] = dp[i - 1] + 1
不能和前两个数构造等差数组:dp[i] = 0 -
初始化
无需初始化。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序很明显是从左往右 -
返回值
题目要求返回所有等差子数组,定义变量sum,一边dp一边累加。
- 代码实现
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {// 1 2 3 4 5//3位置1种 4位置除了拼在3位置可能的后面,还可以抢2 3 来组成//4位置2种 5位置除了拼在4位置可能的后面,还可以抢3 4 来组成//………………对更长的序列也是如此int n = nums.size();//dp[i]:以i位置为结尾的等差数组个数vector<int> dp(n);int sum = 0;for(int i = 2; i < n; i++){//等差数列的性质:num[i] + nums[i - 2] == 2 * num[i - 1]if(nums[i] + nums[i - 2] == 2* nums[i - 1]){dp[i] = dp[i - 1] + 1;}//不满足等差数组为0,vector默认给0,不用处理sum += dp[i];}return sum;//时间复杂度:O(N)//空间复杂度:O(N)}
};
6.最长湍流子数组(中等)
链接:最长湍流子数组
-
题目描述

-
做题步骤
-
状态表示
依据前面的经验,我们定义状态表示为以i位置为结尾的最长湍流子数组长度。
但只知道i-1位置的最大长度是无法推导出i位置的最大长度的,因为不知道前一个最长湍流子数组结束是处于上升状态(最后的比较符号为’<‘)还是下降状态(最后的比较符号为’>')
因此可以对状态进行细分:
(1)f[i]表示以i位置为结尾并处于上升状态(最后的比较符号为’<')的最长湍流子数组长度
(2)g[i]表示以i位置为结尾并处于下降状态(最后的比较符号为’>')的最长湍流子数组长度 -
状态转移方程
因为湍流子数组比较符号必须在每个相邻元素之间翻转,所以状态转移方程与当前的比较符号相关。
(1)arr[i-1] < arr[i],现在处于上升状态,需要前置状态处于下降状态的最长湍流子数组长度,即f[i] = g[i - 1] + 1。
(2)arr[i-1] > arr[i],现在处于下降状态,需要前置状态处于上升状态的最长湍流子数组长度,即g[i] = f[i - 1] + 1。
(3)arr[i-1] = arr[i],不能和前面组合,只能自己重新开始,即f[i] = g[i] = 1。 -
初始化
推导当前状态需要前一个状态,像第一个位置不能跟在别人后面,两个状态的长度都为1,f[0] = g[0] = 1。因为arr[i-1] = arr[i]时f[i] = g[i] = 1,所以干脆一开始全都初始化为1,就不用单独处理arr[i-1] = arr[i]的情况。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序很明显是从左往右 -
返回值
无法直接确定最长湍流数组的结尾位置以及结尾是处于上升还是下降状态,所以定义变量ret,一边dp一边更新最大值。
- 代码实现
class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size();//dp[i]表示以i位置为结尾并且处于上升(下降)状态的最长湍流子数组的长度 vector<int> f(n, 1); //f表示处于上升(<)状态//初始化为1,可以把'=='的情况直接处理了auto g = f; //g表示处于下降(>)状态int ret = 1;for(int i = 1; i < n; i++){if(arr[i-1] < arr[i])f[i] = g[i - 1] + 1;else if(arr[i - 1] > arr[i])g[i] = f[i - 1] + 1;ret = max( {ret, f[i], g[i]} );}return ret;//时间复杂度:O(N)//空间复杂度:O(N)}
};
7.单词拆分(中等)
链接:单词拆分
- 题目描述

- 做题步骤
-
状态表示
依据前面的经验,我们可以定义状态表示为以i位置为结尾的字符串能否由字典中的单词拼出。 -
状态转移方程
以s = “leetcode”, wordDict = [“leet”, “code”]为例进行分析:
(1)先看字符’t’位置(下标3位置),以这个位置为结尾的字符串如果能由字典中的单词拼出,一共有下面几种可能:
①"lee"可以由字典中的单词拼出(即dp[2] = true),"t"也可以由字典中的单词拼出。
②"le"可以由字典中的单词拼出(即dp[1] = true),"et"也可以由字典中的单词拼出。
③"l"可以由单词中的单词拼出(即dp[0] = true),"eet"也可以由字典中的单词拼出。
④再往前就没有了,"leet"可以由字典中的单词拼出。
其它位置的分析也和上述一致,将当前字符串分成[0, j - 1]区间和[j, i]区间,从 0 ~ i 枚举 j ,只要 dp[j - 1] = true并且后面部分的子串 s.substr(j, i - j + 1) 能够在字典中找到,那么 dp[i] = true 。 -
初始化
处理④这样的情况,可以多加一个虚拟节点并初始化true(dp[0] = true),可以理解为空串能在字典中找到。同时为了方便处理下标的映射关系,我们可以在字符串s前面加一个占位符(s = ’ ’ + s),这样就不用考虑下标的映射了。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序很明显是从左往右 -
返回值
根据状态表示,假设字符串长度为n,返回的应该是dp[n] -
优化
为了方便查询字符串是否在字典中,可以把字典的单词存储到哈希表中。
- 代码实现
class Solution
{
public:bool wordBreak(string s, vector<string>& wordDict) {// 将字典⾥⾯的单词存在哈希表⾥⾯unordered_set<string> hash;for(auto& s : wordDict) hash.insert(s);int n = s.size();vector<bool> dp(n + 1);dp[0] = true; // 保证后续填表是正确的s = ' ' + s; // 使原始字符串的下标统⼀ for(int i = 1; i <= n; i++) {for(int j = i; j >= 1; j--) //最后⼀个单词的起始位置{if(dp[j - 1] && hash.count(s.substr(j, i - j + 1))){dp[i] = true;break; //已经确定为真就可以跳出这一层循环了}}}return dp[n];//时间复杂度:O(N^2)//空间复杂度:O(N)}
};
8.环绕字符串中唯⼀的子字符串(中等)
链接:环绕字符串中唯⼀的子字符串
- 题目描述

- 做题步骤
-
状态表示
依据前面的经验,我们定义状态表示为以i位置为结尾并且在base中出现的子字符串个数。 -
状态转移方程
这个题目中的base数组是按照abcd……zabcd这样的顺序来的,要注意base成环。
以i位置为结尾并在base中出现的子字符串有下面三种可能:
(1)不拼在别人后面,就单独自己一个,该字符串一定会在base中出现。
(2)拼在别人后面,并且满足s[i] = s[i - 1] + 1(即满足abcd递增)
(3)拼在别人后面,并且满足s[i] == ‘a’ && s[i - 1] == ‘z’(刚好成环)
综上所述,状态转移方程为:
①满足(2)(3)中任意一个,dp[i] = dp[i - 1] + 1(这个1是自己,dp[i - 1]是拼在别人后面)
②不满足(2)(3),dp[i] = 1 -
初始化
每个位置最少也有自己单独一个的情况,所以全都初始化为1。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序很明显是从左往右 -
返回值
这个题目最需要注意的就是对dp表数据的处理,因为dp表中可能有大量重复的数据,比如"abcdcd"中’d’字符出现了两次,"cd"和"d"这两个字符串在dp表中是多次记录了的,我们需要对dp表数据进行去重。
每个字符都对应了固定的ASCLL码,因此可以可以创建⼀个大小为 26 的数组,遍历dp表,对于出现多次的字符,只需保留以该字符为结尾的最大dp值。
去重完成后再进行累加就可以得到结果。
- 代码实现
class Solution {
public:int findSubstringInWraproundString(string s) {//base是abcd……连续的//s[i]表示现在位置//所以字串要存在要么s[i] == s[i - 1] + 1//要么(s[i - 1] == 'z' && a[i]=='a') int n = s.size();//dp[i]:以i位置为结尾并且在base中出现的子字符串数vector<int> dp(n, 1);for(int i = 1; i < n; i++){if(s[i] == s[i-1] + 1 || (s[i-1] == 'z' && s[i] == 'a')){dp[i] = dp[i - 1] + 1; // 这个1是自己}}int hash[26] = {0};//遍历一次,统计对应字符最大的出现次数//"abcdd"这样的后面那个d的1是无效的,要去掉for(int i = 0; i < n; i++){int index = s[i] - 'a';hash[index] = max(hash[index], dp[i]);}//最后累加int sum = 0;for(auto e : hash){sum += e;}return sum;//时间复杂度:O(N)//空间复杂度:O(N)}
};
相关文章:

动态规划:路径和子数组问题(C++)
动态规划:路径和子数组问题 路径问题1.不同路径(中等)2.不同路径II(中等)3.下降路径最⼩和(中等)4.地下城游戏(困难) 子数组问题1.最大子数组和(中等…...

微服务-gateway跨域配置
文章目录 一、前言二、gateway跨域配置1、问题描述1.1、什么是跨域请求?1.1.1、同源策略1.1.2. 安全性考虑1.1.3. 跨域攻击 1.2、问题产生原因 2、解决方法2.1、修改配置文件2.2、配置类统一配置2.3、全局跨域拦截器 三、总结 一、前言 在SpringCloud项目中&#x…...

爬虫项目(二):中国大学排名
《Python网络爬虫入门到实战》京东购买地址,这里讲解了大量的基础知识和实战,由本人编著:https://item.jd.com/14049708.html配套代码仓库地址:https://github.com/sfvsfv/Crawer文章目录 分析第一步:获取源码分析第一…...

十二、MySQL(DQL)分组/排序/分页查询如何实现?
总括 select 字段列表 from 表名 [where 条件] (group by)/(order by)/(limit) 分组字段名 分组查询 1、分组查询 (1)基础语法: select 字段列表 from 表名 [where 条件] group by 分组字段名 [having 分组之后的过滤条件] (…...

设计模式概念学习
创建类型 单例模式 饿汉 构建时就创建 懒汉 单线程-访问到的时候才创建多线程-低效率 做法:加锁->若未创建则创建->获取资源->解锁 缺点:效率低,每次访问之前都要加锁,资源创建之后不能被同时被多个线程访问多线程-…...
Spring MVC 五 - DispatcherServlet初始化过程(续)
今天的内容是SpringMVC的初始化过程,其实也就是DispatcherServilet的初始化过程。 Special Bean Types DispatcherServlet委托如下一些特殊的bean来处理请求、并渲染正确的返回。这些特殊的bean是Spring MVC框架管理的bean、按照Spring框架的约定处理相关请求&…...

day36:网编day3,TCP、UDP模型
下载: #include <myhead.h>#define ERR(s) do\ {\fprintf(stderr,"__%d__",__LINE__);\perror(s);\ }while(0) #define PORT 69 #define IP "192.168.115.184"int do_download(int cfd,struct sockaddr_in sin); //int do_upload(); int…...

MySQL——MySQL的基础操作部分
使用命令行登录 mysql -u root -p 直接敲击回车后输入密码即可: 当看到出现“mysql>“的符号之后,就表示已经进入到了MySQL系统中,就可以输入My…...

编译OpenWrt内核驱动
编译OpenWrt内核驱动可以参考OpenWrt内部其它驱动的编写例程,来修改成自己需要的驱动 一、OpenWrt源代码获取与编译 1.1、搭建环境 下载OpenWrt的官方源码: git clone https://github.com/openwrt/openwrt.git1.2、安装编译依赖项 sudo apt update -…...
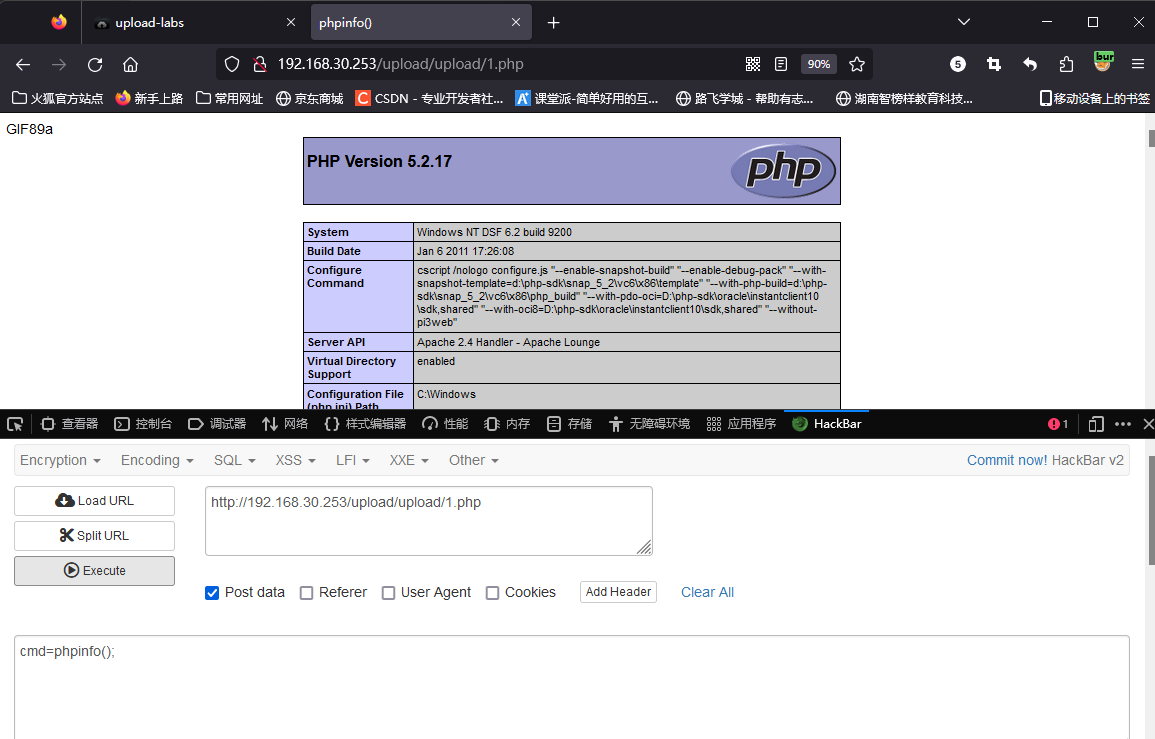
文件上传漏洞-upload靶场5-12关
文件上传漏洞-upload靶场5-12关通关笔记(windows环境漏洞) 简介 在前两篇文章中,已经说了分析上传漏的思路,在本篇文章中,将带领大家熟悉winodws系统存在的一些上传漏洞。 upload 第五关 (大小写绕过…...
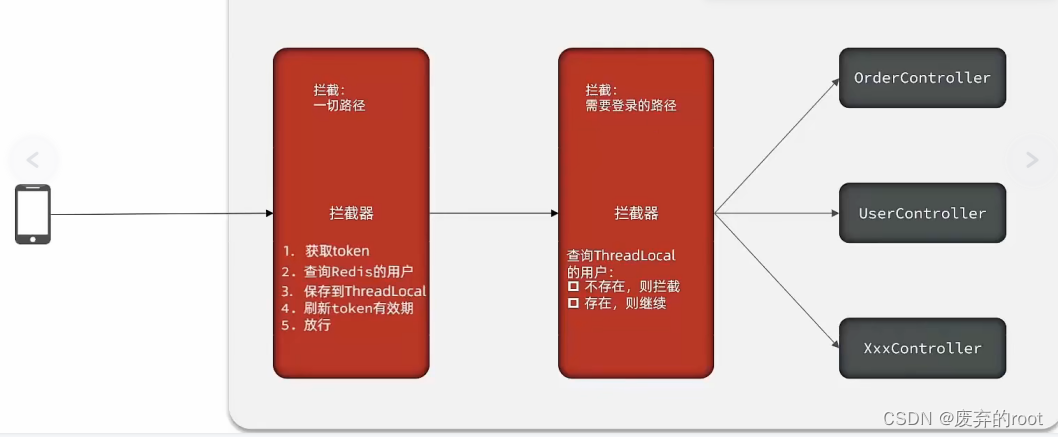
Redis功能实战篇之Session共享
1.使用redis共享session来实现用户登录以及token刷新 当用户请求我们的nginx服务器,nginx基于七层模型走的事HTTP协议,可以实现基于Lua直接绕开tomcat访问redis,也可以作为静态资源服务器,轻松扛下上万并发, 负载均衡…...

leetcode235. 二叉搜索树的最近公共祖先(java)
二叉搜索树的最近公共祖先 题目描述递归 剪枝代码演示: 上期经典 题目描述 难度 - 中等 LC235 二叉搜索树的最近公共祖先 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q…...
2023物联网新动向:WEB组态除了用于数据展示,也支持搭建业务逻辑,提供与蓝图连线和NodeRed规则链类似的可视化编程能力
前言 组态编辑在工业控制、物联网场景中十分常见,越来越多的物联网平台也把组态作为一项标配功能。 物联网产业链自下往上由“端 - 边 - 管 - 云 -用”多个环节构成,组态通常是用于搭建数据展示类型的应用,而随着系统集成度越来越高&#x…...

react将文件转为base64进行上传
需求 将图片、pdf、word、excel等文件进行上传。图片、pdf等调接口A、word、excel等附件调接口B。接口关于文件是base64格式的参数 业务场景 上传资源,区分影像与附件 逻辑思路 使用原生input标签,typefile,进行上传上传后的回调&#x…...

生成式人工智能能否使数字孪生在能源和公用事业行业成为现实?
推荐:使用 NSDT场景编辑器 快速搭建3D应用场景 克服障碍,优化数字孪生优势 要实现数字孪生的优势,您需要数据和逻辑集成层以及基于角色的演示。如图 1 所示,在任何资产密集型行业(如能源和公用事业)中&…...
SpringBoot集成JWT token实现权限验证
JWTJSON Web Token 1. JWT的组成 JWTHeader,Payload,Signature>abc.def.xyz 地址:JSON Web Tokens - jwt.er 1.1 Header Header:标头。 两个组成部分:令牌的类型(JWT)和所使用的签名算法,经过Base64 Url编码后形成…...

算法通关村第11关【青铜】| 位运算基础
1.数字在计算机中的表示 原码、反码和补码都是计算机中用于表示有符号整数的方式。它们的使用旨在解决计算机硬件中的溢出和算术运算问题。 原码(Sign-Magnitude): 原码最简单,它的表示方式是用最高位表示符号位,0表示…...

无涯教程-Android - RadioGroup函数
RadioGroup类用于单选按钮集。 如果我们选中属于某个单选按钮组的一个单选按钮,它将自动取消选中同一组中以前选中的任何单选按钮。 RadioGroup属性 以下是与RadioGroup控制相关的重要属性。您可以查看Android官方文档以获取属性的完整列表以及可以在运行时更改这些属性的相关…...
降噪音频转录 Krisp: v1.40.7 Crack
主打人工智能降噪服务的初创公司「Krisp」近期宣布推出音频转录功能,能对电话和视频会议进行实时设备转录。该软件还整合的ChatGPT,以便快速总结内容,开放测试版于今天上线。 随着线上会议越来越频繁,会议转录已成为团队工作的重…...

基于React实现:弹窗组件与Promise的有机结合
背景 弹窗在现代应用中是最为常见的一种展示信息的形式,二次确认弹窗是其中最为经典的一种。当我们在React,Vue这种数据驱动视图的前端框架中渲染弹窗基本是固定的使用形式。 使用方式:创建新的弹窗组件,在需要弹窗的地方引用并…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
