【LeetCode算法系列题解】第51~55题
CONTENTS
- LeetCode 51. N 皇后(困难)
- LeetCode 52. N 皇后 II(困难)
- LeetCode 53. 最大子序和(中等)
- LeetCode 54. 螺旋矩阵(中等)
- LeetCode 55. 跳跃游戏(中等)
LeetCode 51. N 皇后(困难)
【题目描述】
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
N 皇后问题研究的是如何将 N 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n,返回所有不同的 N 皇后问题的解决方案。
每一种解法包含一个不同的 N 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
【示例1】
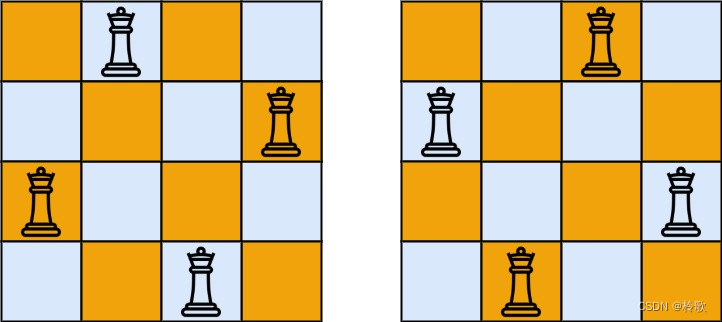
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
【示例2】
输入:n = 1
输出:[["Q"]]
【提示】
1 ≤ n ≤ 9 1\le n\le 9 1≤n≤9
【分析】
N 皇后裸题,DFS 爆搜每一行能放置皇后的位置即可,可以使用 col[i]、dg[i] 以及 udg[i] 分别表示某一列、正对角线与反对角线是否能放皇后(由于我们是按行枚举的因此不用判断某一行是否可以放置)。由于正对角线为 y = x + b y=x+b y=x+b,因此可以用 y − x y-x y−x 唯一确定一条正对角线(可以通过统一加上 n n n 避免越界);同理可以用 y + x y+x y+x 确定一条反对角线。
【代码】
class Solution {
public:vector<vector<string>> res;vector<bool> col, dg, udg;vector<vector<string>> solveNQueens(int n) {col = vector<bool>(n);dg = udg = vector<bool>(n << 1); // 对角线的数量为2n-1vector<string> board(n, string(n, '.')); // 初始化棋盘全为'.'dfs(board, 0); // 从第0行开始搜return res;}void dfs(vector<string>& board, int x){if (x == board.size()) { res.push_back(board); return; }for (int y = 0; y < board.size(); y++)if (!col[y] && !dg[y - x + board.size()] && !udg[y + x]){board[x][y] = 'Q';col[y] = dg[y - x + board.size()] = udg[y + x] = true;dfs(board, x + 1);col[y] = dg[y - x + board.size()] = udg[y + x] = false;board[x][y] = '.';}}
};
LeetCode 52. N 皇后 II(困难)
【题目描述】
N 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n,返回 N 皇后问题不同的解决方案的数量。
【示例1】

输入:n = 4
输出:2
解释:如上图所示,4 皇后问题存在两个不同的解法。
【示例2】
输入:n = 1
输出:1
【提示】
1 ≤ n ≤ 9 1\le n\le 9 1≤n≤9
【分析】
与上一题一样,只需要记录方案数而不需要记录整个棋盘。
【代码】
class Solution {
public:vector<bool> col, dg, udg;int totalNQueens(int n) {col = vector<bool>(n);dg = udg = vector<bool>(n << 1);return dfs(n, 0);}int dfs(int n, int x){if (x == n) return 1;int res = 0;for (int y = 0; y < n; y++)if (!col[y] && !dg[y - x + n] && !udg[y + x]){col[y] = dg[y - x + n] = udg[y + x] = true;res += dfs(n, x + 1);col[y] = dg[y - x + n] = udg[y + x] = false;}return res;}
};
LeetCode 53. 最大子序和(中等)
【题目描述】
给你一个整数数组 nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
【示例1】
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
【示例2】
输入:nums = [1]
输出:1
【示例3】
输入:nums = [5,4,-1,7,8]
输出:23
【提示】
1 ≤ n u m s . l e n g t h ≤ 1 0 5 1\le nums.length\le 10^5 1≤nums.length≤105
− 1 0 4 ≤ n u m s [ i ] ≤ 1 0 4 -10^4\le nums[i]\le 10^4 −104≤nums[i]≤104
【分析】
我们先分析 O ( n ) O(n) O(n) 的算法,用动态规划考虑:令 f[i] 表示所有以 nums[i] 结尾的区间中的最大和,那么状态转移有以下两种情况:
- 区间长度等于1:
f[i] = nums[i]; - 区间长度大于1:
f[i] = f[i - 1] + nums[i]
因此可以得到状态转移方程为:f[i] = max(nums[i], f[i - 1] + nums[i]) = nums[i] + max(0, f[i - 1]),由于 f[i] 只和 f[i - 1] 有关,因此我们可以只使用一个变量记录 f[i - 1] 的值即可。
现在我们考虑如何用分治法求解,其实分治法就是线段树维护动态最大字段和的简化版,当前数组的最大子段所在的区间可能有以下几种情况:
- 在左子区间中,结果即为左子区间的最大子段;
- 在右子区间中,结果即为右子区间的最大子段;
- 横跨左右两个子区间,结果即为左子区间的最大后缀加上右子区间的最大前缀;
求解最大前缀与最大后缀时可能还会有以下几种情况:
- 最大前缀横跨左右两个子区间,那么最大前缀为左子区间的总和加上右子区间的最大前缀;
- 最大后缀横跨左右两个子区间,那么最大后缀为右子区间的总和加上左子区间的最大后缀;
因此我们需要处理出每个区间的最大子段、最大前缀、最大后缀以及总长度这四个信息。
【代码】
【动态规划实现】
class Solution {
public:int maxSubArray(vector<int>& nums) {int res = INT_MIN;for (int i = 0, f = 0; i < nums.size(); i++)f = nums[i] + max(f, 0), res = max(res, f);return res;}
};
【分治法实现】
class Solution {
public:struct Node {int sum, lmax, rmax, tmax; // 区间和,最大前缀,最大后缀,最大子段和};int maxSubArray(vector<int>& nums) {auto t = build(nums, 0, nums.size() - 1);return t.tmax;}Node build(vector<int>& nums, int l, int r){if (l == r) return { nums[l], nums[l], nums[l], nums[l] }; // 递归到了长度为1的结点int mid = l + r >> 1;auto lnode = build(nums, l, mid), rnode = build(nums, mid + 1, r);// 线段树中的pushup操作Node res;res.sum = lnode.sum + rnode.sum;res.lmax = max(lnode.lmax, lnode.sum + rnode.lmax);res.rmax = max(rnode.rmax, rnode.sum + lnode.rmax);res.tmax = max(max(lnode.tmax, rnode.tmax), lnode.rmax + rnode.lmax);return res;}
};
LeetCode 54. 螺旋矩阵(中等)
【题目描述】
给你一个 m 行 n 列的矩阵 matrix,请按照顺时针螺旋顺序,返回矩阵中的所有元素。
【示例1】
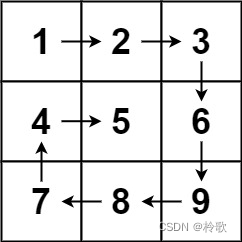
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
【示例2】
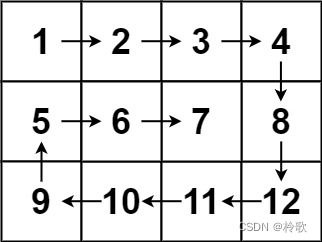
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
【提示】
m = = m a t r i x . l e n g t h m == matrix.length m==matrix.length
n = = m a t r i x [ i ] . l e n g t h n == matrix[i].length n==matrix[i].length
1 ≤ m , n ≤ 10 1\le m, n\le 10 1≤m,n≤10
− 100 ≤ m a t r i x [ i ] [ j ] ≤ 100 -100\le matrix[i][j]\le 100 −100≤matrix[i][j]≤100
【分析】
分别设置向右、向下、向左、向上四个方向向量,然后模拟一遍即可,走出界或是已经遍历过了改变一下方向即可。
【代码】
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int n = matrix.size(), m = matrix[0].size();int dx[] = { 0, 1, 0, -1 }, dy[] = { 1, 0, -1, 0 };vector<int> res;for (int i = 0, x = 0, y = 0, d = 0; i < n * m; i++) // 总共遍历n*m个点{res.push_back(matrix[x][y]);matrix[x][y] = INT_MIN; // 遍历过的数修改为INT_MINint nx = x + dx[d], ny = y + dy[d];if (nx < 0 || nx >= n || ny < 0 || ny >= m || matrix[nx][ny] == INT_MIN) d = (d + 1) % 4;x += dx[d], y += dy[d];}return res;}
};
LeetCode 55. 跳跃游戏(中等)
【题目描述】
给你一个非负整数数组 nums,你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true;否则,返回 false。
【示例1】
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
【示例2】
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
【提示】
1 ≤ n u m s . l e n g t h ≤ 1 0 4 1\le nums.length\le 10^4 1≤nums.length≤104
0 ≤ n u m s [ i ] ≤ 1 0 5 0\le nums[i]\le 10^5 0≤nums[i]≤105
【分析】
本题和第45题差不多,我们从小到大枚举 i i i,并同时维护 i i i 之前所有点能跳到的最远距离 m a x _ d i s max\_dis max_dis,如果 max_dis < i,说明 i i i 之前没有点能够跳到 i i i 了,直接返回 false 即可。
【代码】
class Solution {
public:bool canJump(vector<int>& nums) {for (int i = 0, max_dis = 0; i < nums.size(); i++){if (max_dis < i) return false;max_dis = max(max_dis, i + nums[i]);}return true;}
};
相关文章:

【LeetCode算法系列题解】第51~55题
CONTENTS LeetCode 51. N 皇后(困难)LeetCode 52. N 皇后 II(困难)LeetCode 53. 最大子序和(中等)LeetCode 54. 螺旋矩阵(中等)LeetCode 55. 跳跃游戏(中等) …...
驱动开发错误汇编
本博文将会不定期更新。以便记录我的驱动开发生涯中的一些点点滴滴的技术细节和琐事。 1. link阶段找不到导出函数 比如"LNK2019 无法解析的外部符号 _FltCreateCommunicationPort32"。 出现这种情况的原因是,驱动的编译环境忽略了所有的默认库&#x…...
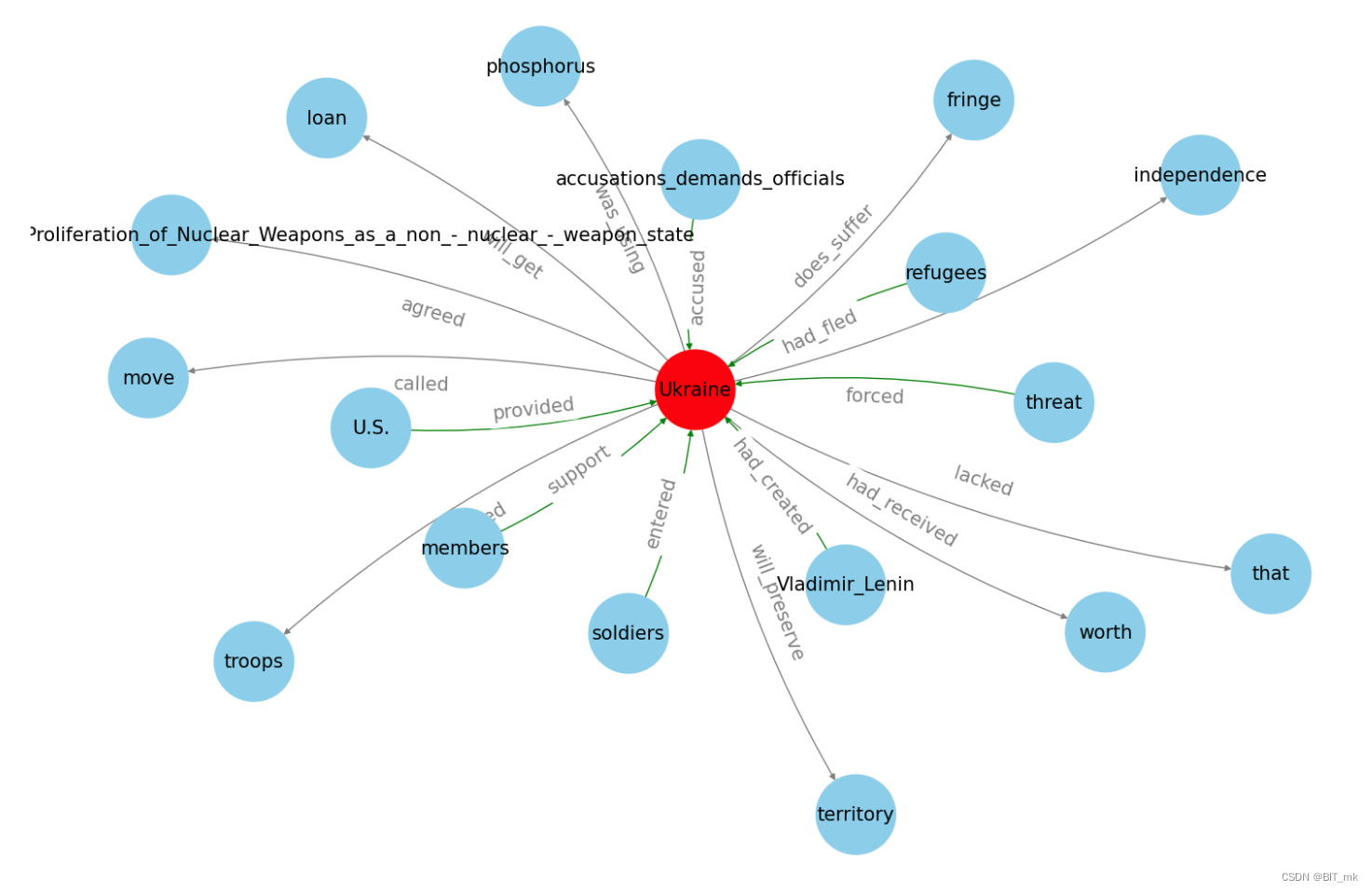
知识图谱项目实践
目录 步骤 SpaCy Textacy——Text Analysis for Cybersecurity Networkx Dateparser 导入库 写出页面的名称 编辑 自然语言处理 词性标注 可能标记的完整列表 依存句法分析(Dependency Parsing,DEP) 可能的标签完整列表 实例理…...

stable diffusion实践操作-提示词-人物属性
系列文章目录 stable diffusion实践操作-提示词 文章目录 系列文章目录前言一、提示词汇总1.1 人物属性11.2 人物属性2 前言 本文主要收纳总结了提示词-人物属性。 一、提示词汇总 1.1 人物属性1 角色类型人物身材胸部头发-发型头发-发色[女仆][霊烏路空][大腿][乳房][呆毛…...

RabbitMQ的安装和配置
将RabbitMQ文件夹传到linux根目录 开启管理界面及配置...

WebRTC 日志
WebRTC 日志 flyfish WebRTC支持的日志等级 // // The meanings of the levels are: // LS_VERBOSE: This level is for data which we do not want to appear in the // normal debug log, but should appear in diagnostic logs. // LS_INFO: Chatty level used in de…...
【python爬虫】16.爬虫知识点总结复习
文章目录 前言爬虫总复习工具解析与提取(一)解析与提取(二)更厉害的请求存储更多的爬虫更强大的爬虫——框架给爬虫加上翅膀 爬虫进阶路线指引解析与提取 存储数据分析与可视化更多的爬虫更强大的爬虫——框架项目训练 反爬虫应对…...
Windows系统中Apache Http服务器简单使用
1 简介 Apache HTTP服务器是一个开源的、跨平台的Web服务器软件。它由Apache软件基金会开发和维护。Apache HTTP服务器可以在多种操作系统上运行,如Windows、Linux、Unix等,并且支持多种编程语言和技术,如PHP、Perl、Python、Java等。…...
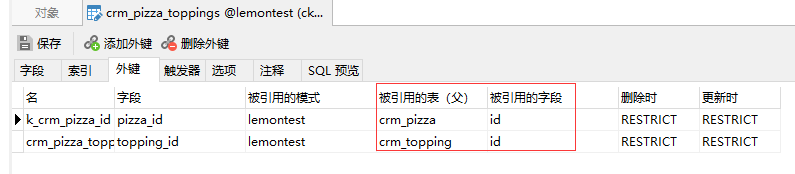
Django ORM 框架中的表关系,你真的弄懂了吗?
Django ORM 框架中的表关系 为了说清楚问题,我们设计一个 crm 系统,包含五张表: 1.tb_student 学生表 2.tb_student_detail 学生详情表 3.tb_salesman 课程顾问表 4.tb_course 课程表 5.tb_entry 报名表 表关系和字段如下图:…...

第五课:C++实现加密PDF文档解密
请注意,未经授权的加密PDF文件解密是非法的,本文仅为学术和研究目的提供参考。 打开加密的PDF文件并获取密钥 在C++中,可以使用pdfium库打开加密的PDF文件。使用pdfium库中的FPDF_LoadCustomDocument函数可以打开具有自定义访问权限的加密文件。该函数接受一个IFX_FileRead*…...

罗马数字转整数
罗马数字转整数 题目: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M …...
processflow流程图多人协作预热
前言 在线上办公如火如荼的今天,多人协作功能是每个应用绕不开的门槛。processflow在线流程图(前身基于drawio二次开发)沉寂两年之久,经过长时间设计开发,调整,最终完成了多人协作的核心模块设计。废话不多…...
)
PCL点云处理之快速计算多个点到同一直线的距离(二百零五)
PCL点云处理之快速计算多个点到同一直线的距离(二百零五) 一、算法简介二、具体实现1.代码2.结果一、算法简介 点到直线的距离计算,是一种常用的算法,在点云处理中,经常遇到需要计算多个点云到同一条直线的距离计算需求,此时若是逐点计算将耗费大量的时间,熟悉点到直线…...

xxl-job 任务调度搭建及简单使用
xxl-job是开源架构,可以通过它实现调度中心和执行器。 git地址和 官网中进行了详细的技术说明。 xxl-job支持单机部署和集群式部署,在集群式部署中又可以实现调度中心集群式部署和执行器集群式部署。本文主要针对调度中心和执行器分离单机部署方式进…...
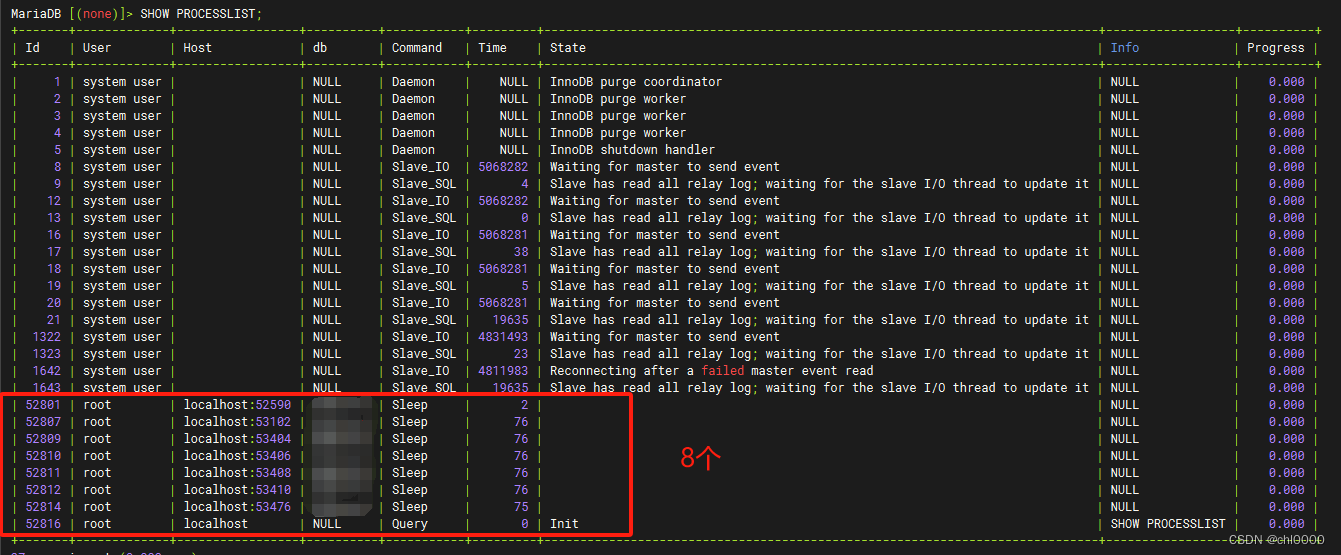
mysql数据库使用技巧整理
查看当前数据库已建立的client连接 > SHOW VARIABLES LIKE max_connections; -- 查看数据库允许的最大连接数,不是实时正在使用的连接数 > SHOW STATUS LIKE Threads_connected; -- 查看当前数据库client的连接数 > SHOW PROCESSLIST; -- 查看具体的连接...

车规微控制器的ECC机制及EMU外设
车规微控制器的ECC机制及EMU外设 文章目录 车规微控制器的ECC机制及EMU外设引言ECC的基本原理ECC RAM的访问方式ECC RAM的初始化SRAM ECC错误注入及EMU外设Flash ECC校验参考文献 引言 ECC是微控制器系统中,用于保障信息安全的常用机制,主要是避免存储设…...

Less的强大变量用法
less中的变量应用十分强大,可以灵活的应用到各种不同需求的场景。 一,属性值变量 声明:sass声明变量是用$符号,而less声明变量是用符号 作用域:也区分为全局变量和局部变量,如果引用的变量有定义局部变量&…...

【相机标定】opencv python 标定相机内参时不计算 k3 畸变参数
文章目录 1. 背景2. 完整的 opencv python 标定相机内参过程3. 选择是否计算畸变参数 k3 1. 背景 畸变参数 k3 通常用于描述径向畸变的更高阶效应,即在需要高精度的应用中可以用到,一般的应用中 k1, k2 足矣。 常见的应用中, orbslam3 中是否…...
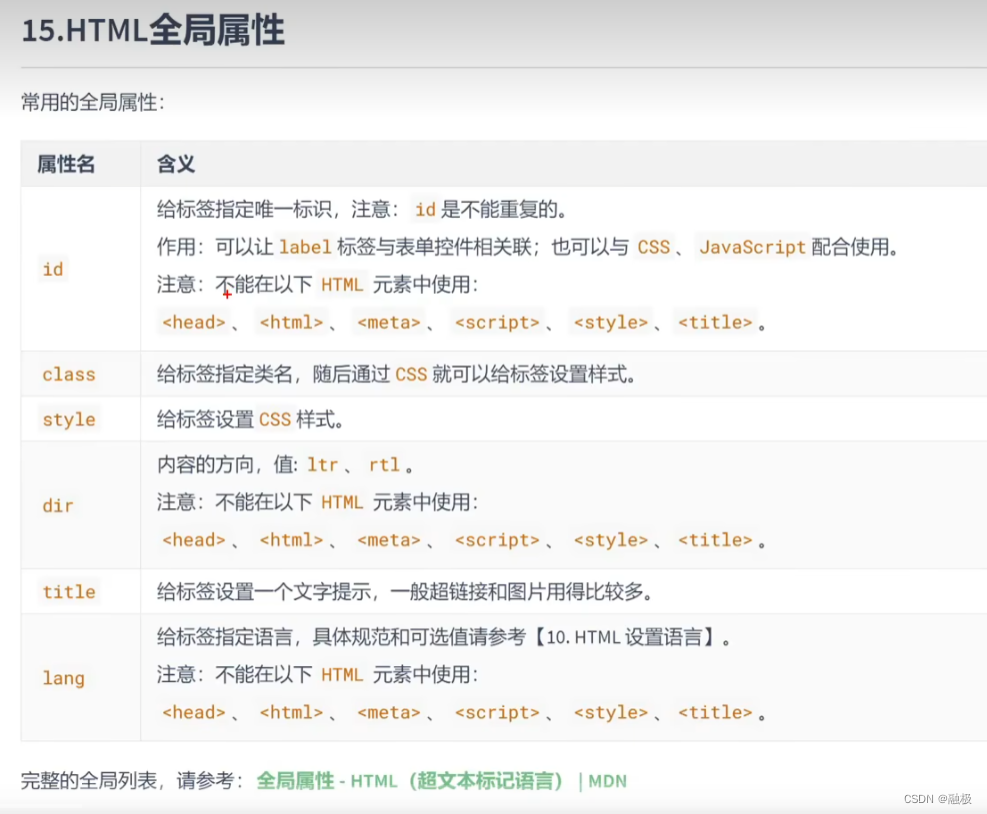
html 标签简介
概述 标签的效果不重要,重要的是标签的语义。 文本标签 文本标签用于包裹:词汇、短语等。排版标签,比如div,p,h1等。排版标签更宏观(大段的文字),文本标签更微观(词汇、短语)。文…...

dos汇编总结
前言: 计组课本需要学习汇编,可惜自己看不太懂。这里发现一个学习方法交给大家。其实新手可能一些抽象表示难理解,这里我把我学习的疑问点以及思路记录一下。 要点: 这里我以题为例给大家分析 输出输入对应大写字母的小写字母 …...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
