空间曲线的参数方程
空间曲线的参数方程
二维直线
经过一点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)的方向向量为 n ( c o s θ , s i n θ ) n(cos\theta,sin\theta) n(cosθ,sinθ)的直线参数方程为:
[ x y ] = [ x 0 y 0 ] + t [ c o s θ s i n θ ] t ∈ [ 0 , 2 π ) \begin{bmatrix} x\\ y \end{bmatrix} =\begin{bmatrix} x_0\\ y_0 \end{bmatrix} +t\begin{bmatrix} cos\theta\\ sin\theta \end{bmatrix} \hspace{2em} t\in [0,2\pi) [xy]=[x0y0]+t[cosθsinθ]t∈[0,2π)
三维直线
经过一点 P ( x 0 , y 0 , z 0 ) P(x_0,y_0,z_0) P(x0,y0,z0)的单位方向向量为 n ( i , j , k ) n(i,j,k) n(i,j,k)的直线参数方程为:
[ x y z ] = [ x 0 y 0 z 0 ] + t [ i j k ] t ∈ [ 0 , 2 π ) \begin{bmatrix} x\\ y\\ z \end{bmatrix} =\begin{bmatrix} x_0\\ y_0\\ z_0 \end{bmatrix} +t\begin{bmatrix} i\\ j\\ k \end{bmatrix} \hspace{2em} t\in [0,2\pi) xyz = x0y0z0 +t ijk t∈[0,2π)
二维圆
经过圆心 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0),半径为 r r r,的圆参数方程为:
[ x y ] = [ x 0 y 0 ] + r [ c o s θ s i n θ ] θ ∈ [ 0 , 2 π ) \begin{bmatrix} x\\ y \end{bmatrix} =\begin{bmatrix} x_0\\ y_0 \end{bmatrix} +r\begin{bmatrix} cos\theta\\ sin\theta \end{bmatrix} \hspace{2em} \theta\in [0,2\pi) [xy]=[x0y0]+r[cosθsinθ]θ∈[0,2π)
三维圆
经过圆心 P ( x 0 , y 0 , z 0 ) P(x_0,y_0,z_0) P(x0,y0,z0),半径为 r r r,且该圆所在的平面正交的两个单位向量 e 1 ⃗ ( a x , a y , a z ) , e 2 ⃗ ( b x , b y , b z ) \vec{e_1}(a_x,a_y,a_z),\vec{e_2}(b_x,b_y,b_z) e1(ax,ay,az),e2(bx,by,bz)的圆参数方程为:
[ x y z ] = [ x 0 y 0 z 0 ] + r c o s θ [ a x a y a z ] + r s i n θ [ b x b y b z ] θ ∈ [ 0 , 2 π ) \begin{bmatrix} x\\ y\\ z \end{bmatrix}= \begin{bmatrix} x_0\\ y_0\\ z_0 \end{bmatrix} +rcos\theta\begin{bmatrix} a_x\\ a_y\\ a_z \end{bmatrix} +rsin\theta\begin{bmatrix} b_x\\ b_y\\ b_z \end{bmatrix} \hspace{2em} \theta\in [0,2\pi) xyz = x0y0z0 +rcosθ axayaz +rsinθ bxbybz θ∈[0,2π)
特殊情况下,当 e 1 ⃗ ( a x , a y , a z ) , e 2 ⃗ ( b x , b y , b z ) \vec{e_1}(a_x,a_y,a_z),\vec{e_2}(b_x,b_y,b_z) e1(ax,ay,az),e2(bx,by,bz)分别为 e 1 ⃗ ( 1 , 0 , 0 ) , e 2 ⃗ ( 0 , 1 , 0 ) \vec{e_1}(1,0,0),\vec{e_2}(0,1,0) e1(1,0,0),e2(0,1,0)时,公式(4) 简化为:
[ x y z ] = [ x 0 y 0 z 0 ] + r [ c o s θ s i n θ 0 ] θ ∈ [ 0 , 2 π ) \begin{bmatrix} x\\ y\\ z \end{bmatrix} =\begin{bmatrix} x_0\\ y_0\\ z_0 \end{bmatrix} +r\begin{bmatrix} cos \theta \\ sin \theta \\ 0 \end{bmatrix} \hspace{2em} \theta \in [0,2 \pi) xyz = x0y0z0 +r cosθsinθ0 θ∈[0,2π)
任意平面内的圆,可以先计算基准坐标系中的圆然后通过坐标变换 ,将问题转化为,转换为所求平面内的圆。
图形化表示:


如何快速求解 e 1 ⃗ ( a x , a y , a z ) , e 2 ⃗ ( b x , b y , b z ) \vec{e_1}(a_x,a_y,a_z),\vec{e_2}(b_x,b_y,b_z) e1(ax,ay,az),e2(bx,by,bz)?
- 求解 e 1 ⃗ \vec{e_1} e1,将圆所在平面的法向量与坐标向量 i ⃗ \vec{i} i叉乘,然后单位化即可得到,如果叉乘结果为0 ,就叉乘 j ⃗ \vec{j} j,再者就叉乘 k ⃗ \vec{k} k;
- 求解 e 2 ⃗ \vec{e_2} e2,就将法向量与 e 1 ⃗ \vec{e_1} e1叉乘即可。
对应的python代码:
\sum_{s}^{} {\textstyle \sum_{}^{}} # 对应的版本matplotlib 3.7.1 py311h06a4308_1
from matplotlib import pyplot as plt
import numpy as npnormal_direction = np.array([1, 1, 1])
radius = 1
center = np.array([1, 1, 1])
pi = 3.1415926
theta = np.array([])for i in range(100):theta = np.append(theta, 2.0 * pi * i / 100)theta = np.array(theta)
e1 = np.cross(normal_direction, [0, 1, 0])
if np.linalg.norm(e1) < 1e-10:e1 = np.cross(normal_direction, [0, 1, 0])e2 = np.cross(normal_direction, e1)# 单位化
e1_norm = e1 / np.linalg.norm(e1)
e2_norm = e2 / np.linalg.norm(e2)
size = np.size(theta)x0 = center[0] * np.ones(size)
y0 = center[1] * np.ones(size)
z0 = center[2] * np.ones(size)x = x0 + radius * e1[0] * np.cos(theta) + radius * e2[0] * np.sin(theta)
y = y0 + radius * e1[1] * np.cos(theta) + radius * e2[1] * np.sin(theta)
z = z0 + radius * e1[2] * np.cos(theta) + radius * e2[2] * np.sin(theta)# 建立画布
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.set_xlim(-2, 6)
ax.set_ylim(-2, 6)
ax.set_zlim(-2, 6)ax.plot3D(x, y, z, 'r')
plt.show()print("YES PF!")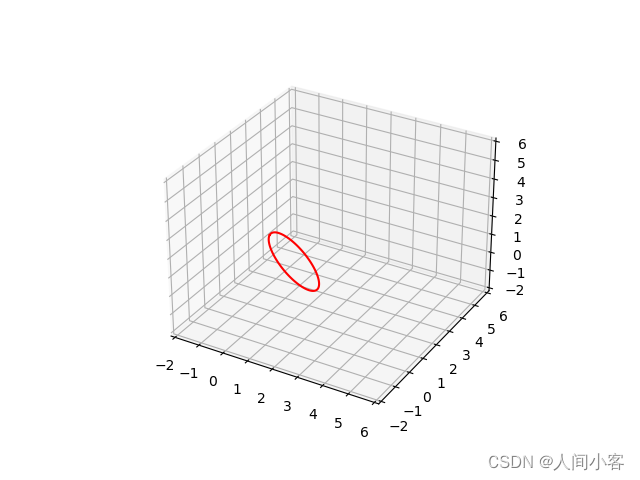
对应的MATLAB代码
Figure_1normal=[1 1 1]; %法向量n
radius=1; %圆的半径为1
center=[1 1 1]; %圆心的坐标
theta=(0:2*pi/100:2*pi)'; %theta角从0到2*pie1=cross(normal,[1 0 0]); %n与i叉乘,求取a向量
if ~any(e1) %如果a为零向量,将n与j叉乘e1=cross(normal,[0 1 0]);
ende2=cross(normal,e1); %求取b向量
e1=e1/norm(e1); %单位化a向量
e2=e2/norm(e2); %单位化b向量x0=center(1)*ones(size(theta,1),1);
y0=center(2)*ones(size(theta,1),1);
z0=center(3)*ones(size(theta,1),1);x=x0+radius*e1(1)*cos(theta)+radius*e2(1)*sin(theta);%圆上各点的x坐标
y=y0+radius*e1(2)*cos(theta)+radius*e2(2)*sin(theta);%圆上各点的y坐标
z=z0+radius*e1(3)*cos(theta)+radius*e2(3)*sin(theta);%圆上各点的z坐标plot3(x,y,z)
xlabel('x轴')
ylabel('y轴')
zlabel('z轴')
三维椭圆
在实际工程化的应用的时候,往往不是圆,而是退化成椭圆,甚至退化成一条直线。
工程中更多是使用椭圆模型,通过检测到的点来确定椭圆的参数,最后确定椭圆的中心点和方向向量。
三维椭圆的参数方程易知:
[ x y z ] = [ x 0 y 0 z 0 ] + a c o s θ [ a x a y a z ] + b s i n θ [ b x b y b z ] θ ∈ [ 0 , 2 π ) \begin{bmatrix} x\\ y\\ z \end{bmatrix} =\begin{bmatrix} x_0\\ y_0\\ z_0 \end{bmatrix} +acos\theta\begin{bmatrix} a_x\\ a_y\\ a_z \end{bmatrix} + bsin\theta\begin{bmatrix} b_x\\ b_y\\ b_z \end{bmatrix} \hspace{2em} \theta\in [0,2\pi) xyz = x0y0z0 +acosθ axayaz +bsinθ bxbybz θ∈[0,2π)
其中 a , b a,b a,b分别表示为椭圆的长半轴长度,短半轴长度 。其余跟圆类似不作具体说明。
椭圆一般化方程为:
c 1 x 2 + c 2 x y + c 3 y 2 + c 4 x + c 5 y + c 6 = 0 c_1x^2+c_2xy+c_3y^2+c_4x+c_5y+c_6 = 0 c1x2+c2xy+c3y2+c4x+c5y+c6=0
可以看到至少使用五个不同点可以确定这六个参数。
一般情况是点的个数远超过5个,处理步骤为:
-
首先使用RANSAC筛选异常点
-
构建误差 d i = c 1 x 2 + c 2 x y + c 3 y 2 + c 4 x + c 5 y + c 6 d_i = c_1x^2+c_2xy+c_3y^2+c_4x+c_5y+c_6 di=c1x2+c2xy+c3y2+c4x+c5y+c6
-
构建代价函数,使用最小二乘求解// 或者SVD分解
c i = a r g m i n Σ d j 2 s , t { ∑ i = 1 6 c i 2 = 1 i ∈ [ 1 , 6 ] , j ∈ [ 1 , n ] {c_i} = argmin\Sigma d_j^2 \hspace{2em} s,t \left\{\begin{matrix} \hspace{1em} \sum_{i=1}^{6}c_i^2 = 1 \\ \hspace{1em} i\in[1,6], \\ \hspace{1em}j\in [1,n] \end{matrix}\right. ci=argminΣdj2s,t⎩ ⎨ ⎧∑i=16ci2=1i∈[1,6],j∈[1,n] -
假设获得 c i c_i ci ,求解对应的圆心和法向量
使用二次型构造,对称矩阵,进行分解,则特征值满足:
λ 1 ≥ λ 2 > 0 > λ 3 \lambda_1 \ge\lambda_2>0>\lambda_3 λ1≥λ2>0>λ3
如果不满足,改变构造的对称矩阵的符号,重新求解对特征值这里直接给出结论:
H H H为分解矩阵后的特征向量组成的正交矩阵,法向量 n ⃗ \vec{n} n,和中心点 P P P为:
c o s 2 φ = λ 2 − λ 3 λ 1 − λ 3 n ⃗ = ± H [ − s i n φ 0 c o s φ ] P = ± H [ − λ 3 / λ 1 s i n φ 0 − λ 1 / λ 3 c o s φ ] cos^2\varphi = \frac{\lambda_2-\lambda_3}{\lambda_1-\lambda_3} \\ \\ \vec{n} = \pm H\begin{bmatrix} -sin\varphi \\ 0 \\ cos\varphi \end{bmatrix} \\ \\ P=\pm H \begin{bmatrix} -\sqrt{\lambda_3/\lambda_1}sin\varphi \\ 0 \\ \sqrt{-\lambda_1/\lambda_3}cos\varphi \end{bmatrix} cos2φ=λ1−λ3λ2−λ3n=±H −sinφ0cosφ P=±H −λ3/λ1sinφ0−λ1/λ3cosφ
参考链接:
- 空间曲线参数方程
- 空间圆的方程
相关文章:

空间曲线的参数方程
空间曲线的参数方程 二维直线 经过一点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)的方向向量为 n ( c o s θ , s i n θ ) n(cos\theta,sin\theta) n(cosθ,sinθ)的直线参数方程为: [ x y …...

非华为机型如何体验HarmonyOS鸿蒙系统 刷写HarmonyOS鸿蒙GSI系统以及一些初步的bug修复
最近很多视频网站有非华为机型使用HarmonyOS鸿蒙系统的演示。其实大都是刷了HarmonyOS鸿蒙系统gsi系统。体验还可以。有些刷入后bug较多。那么这些机型是如何刷写gsi?可以参考我以往帖子 安卓玩机搞机-----没有第三方包 刷写第三方各种GSI系统 体验非官方系统_gsi刷…...

Flutter 生成小程序的混合 App 实践
一、背景 微信小程序发展的越来越快,目前小程序甚至取代了大部分 App 的生态位,公司的坑位不增反降,只能让原生应用开发兼顾或换岗进行小程序的开发。 以我的实际情况来讲,公司应用采用的 Flutter 框架,同样的功能不可避免的就会存在 Flutter 应用开发和微信小程序开发兼…...

利用 Python-user-agents 解析 User_Agent
利用 Python-user-agents 解析 User_Agen 需求分析 近期在尝试做一个登录日志的功能,及用户登录成功后我在后台进行一个用户的登录记录,两种解决方案: 由前端得到用户的手机型号,我在后台接收后在数据库进行保存使用User_Agent…...
Java版企业电子招标采购系统源码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看…...

Mybatis如何给字段起别名?
Mybatis如何给字段起别名? 假如有一个学生表,有一个字段是class,你的实体类变量肯定不能用class,那么如何起别名? 通过以下代码实现 Result(column "class",property "clas")mapper代码 pub…...
php对接AWS S3云存储,上传S3及访问权限问题
首先先下载sdk包 https://docs.aws.amazon.com/zh_cn/sdk-for-php/v3/developer-guide/getting-started_installation.html S3创建存储桶 去安全凭证-》创建访问秘钥 创建的时候会提示,主账号创建不安全,这个时候我们需要创建一个IAM账号来创建秘钥 创…...

java 实现单例模式
单例模式是一种设计模式,用于确保一个类只有一个实例,并提供一种全局访问该实例的方式。在Java中,可以使用多种方式来实现单例模式,下面整理了几种常见的实现方式。 饿汉式单例模式(Eager Initialization)&…...

minio文件服务器开启https
一、准备证书 你要有https安全证书,我的是适用于nginx的证书 私钥 xxxx.key 公钥 xxxx.pem 二、上传证书到minio服务器 然后看看你的minio docker 有没有把 /root/.minio 挂载在主机上,如果有那么把两个证书文件放在/root/.minio/certs目录里面。…...

每日刷题(回溯法经典问题之子集)
食用指南:本文为作者刷题中认为有必要记录的题目 前置知识:回溯法经典问题之组合 ♈️今日夜电波:想着你—郭顶 1:09 ━━━━━━️💟──────── 4:15 …...

PostgreSQL在进行除法时要注意
背景 整型除以整型,正常情况下当然得到的应该也是整型。数据库也是这么干的。 但是在数据库应用中,通常业务的需求是得到NUMERIC,不能直接把小数干掉。 数据库的行为给用户带来了诸多不便,例如1除以2,如果是整型除法会…...
开开心心带你学习MySQL数据库之第五篇
😺欢迎来到我的博客, 记得点赞👍收藏⭐️留言✍️🐱 🐉做为一个怪兽,我的目标是少消灭一个奥特曼🐉 📖希望我写的博客对你有所帮助,如有不足,请指正📖 chatgpt 是否能够代替程序猿?…...

Geotools对geojson的解析
在 GeoTools 中,对 GeoJSON 的支持是通过一个插件来完成的,用户同样可以在 Maven 的 pom.xml 配置文件中添加下述的依赖。 <dependency><groupId>org.geotools</groupId><artifactId>gt-geojson</artifactId><version&…...

【博客701】shell实现保留网络现场:ping失败时执行mtr
shell实现保留网络现场:ping失败时执行mtr 场景 当我们网络出现抖动,到某个目的地ping不通时,我们想知道路径上哪里出现问题时可以在那时候执行mtr并保留下现场以供排查 实现:ping_and_mtr.sh #!/bin/bash# 定义要ping的IP地址列…...
放弃手写代码吧!用低代码你能生成各种源码
很多同学不知道为什么要用Low-code做开发,传统IT开发不行么?当然可以。 传统IT自研软件开发,通过编程去写代码,还有数据库、API、第三方基础架构等。这个方式很好,但不可避免的会带来开发周期长、难度大,技…...

什么程度才算精通 Linux?
前言 Linux 的优秀之处自然不必多说。 如果将操作系统比作一辆汽车,那 Linux 就是一辆性能出色的多功能越野车,上山下海飞天无所不能。 如果你拥有了它,一定不会只满足于驾驶它上下班,不能只会挂挡、踩油门和控制方向之类的基本…...

jmeter中的__setProperty用法
__setProperty 是一个用于设置 JMeter 属性的函数,基本语法: __setProperty(property, value)** property : 是要设置的属性的名称 ** value : 是要设置的属性的值在 JMeter中,可以使用 __setProperty 函数的元素: BeanShell …...
vue基础知识六:v-show和v-if有什么区别?使用场景分别是什么?
一、v-show与v-if的共同点 我们都知道在 vue 中 v-show 与 v-if 的作用效果是相同的(不含v-else),都能控制元素在页面是否显示 在用法上也是相同的 <Model v-show"isShow" /> <Model v-if"isShow" />当表达式为true的时候&#…...

SpringBoot几个常用的注解
(1)RestController和Controller指定一个类,作为控制器的注解 (2)RequestMapping方法级别的映射注解,这一个用过Spring MVC的小伙伴相信都很熟悉 (3)EnableAutoConfiguration和Spri…...

腾讯JAVA后端秋招面试总结
腾讯秋招的面经,岗位是 java 后端开发。 说一下BIO、NIO和AIO 答: BIO是阻塞IO。在上一个线程的任务执行完之前,该线程必须阻塞等待上一个线程执行完毕。 NIO是非阻塞IO。一旦是响应事件发生了,该线程就会将对应的响应事件交给对应的事件处理器进行处理。 AIO是异步IO。主…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...
【QT控件】显示类控件
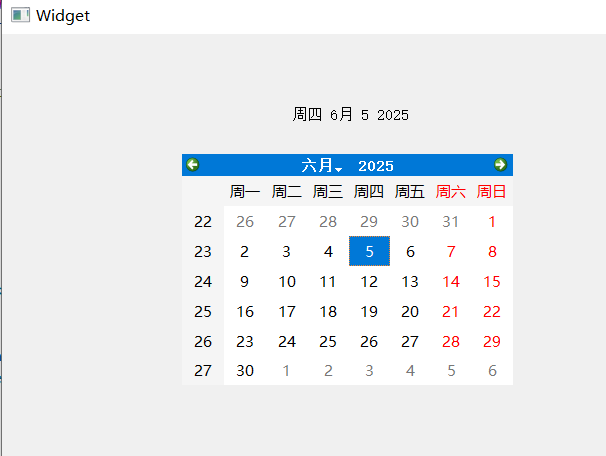
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
