【算法】归并排序 详解
归并排序 详解
- 归并排序
- 代码实现
- 1. 递归版本
- 2. 非递归版本
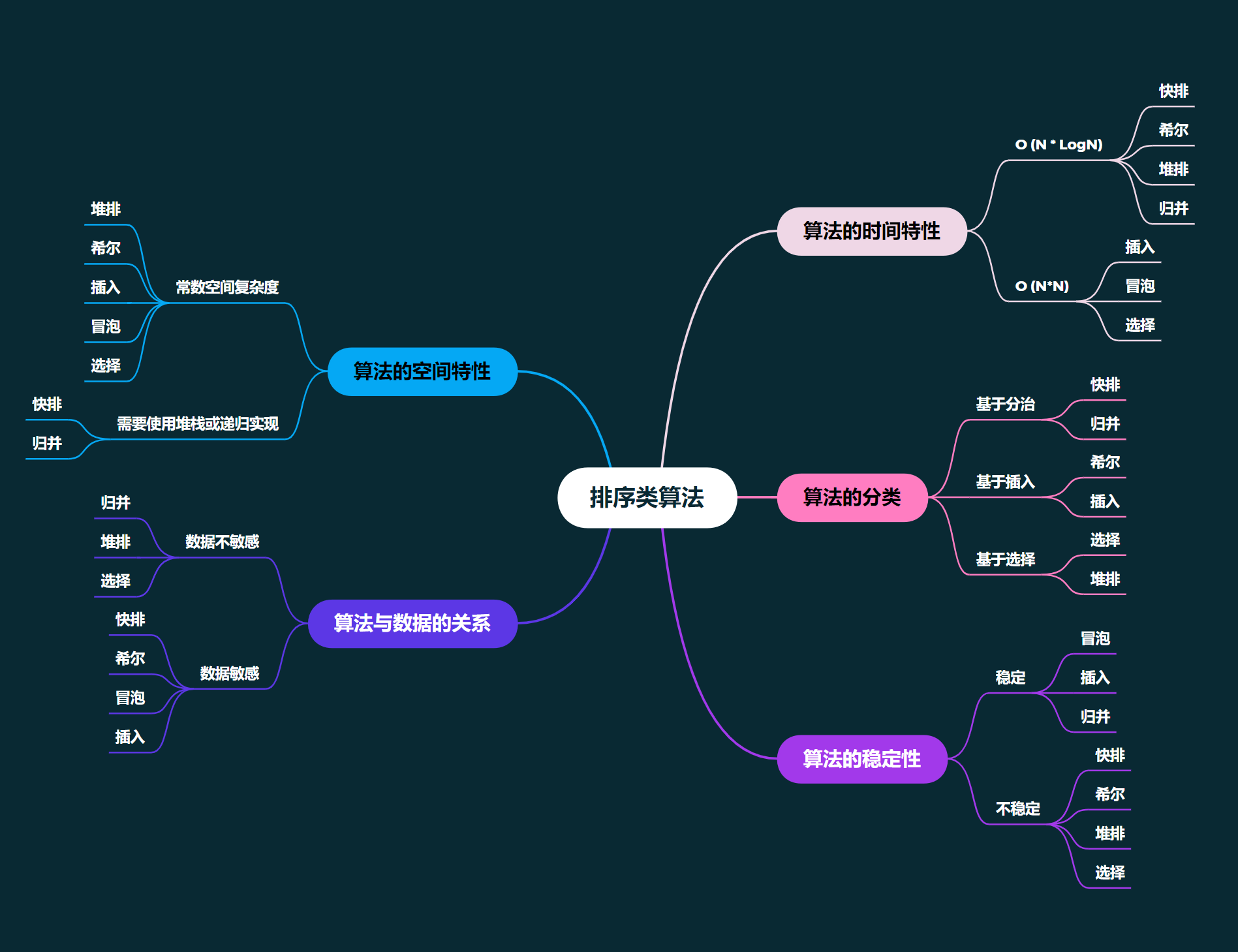
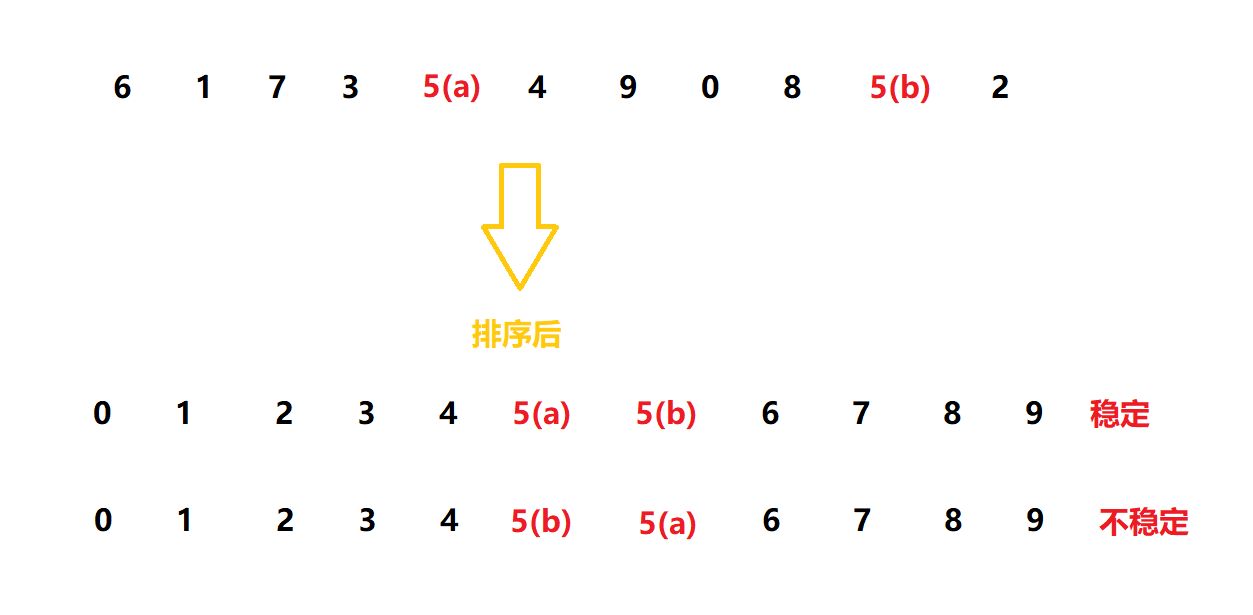
排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中, r[i] = r[j], 且 r[i] 在 r[j] 之前,而在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
(注意稳定排序可以实现为不稳定的形式, 而不稳定的排序实现不了稳定的形式)
内部排序: 数据元素全部放在内存中的排序。
外部排序: 数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
归并排序
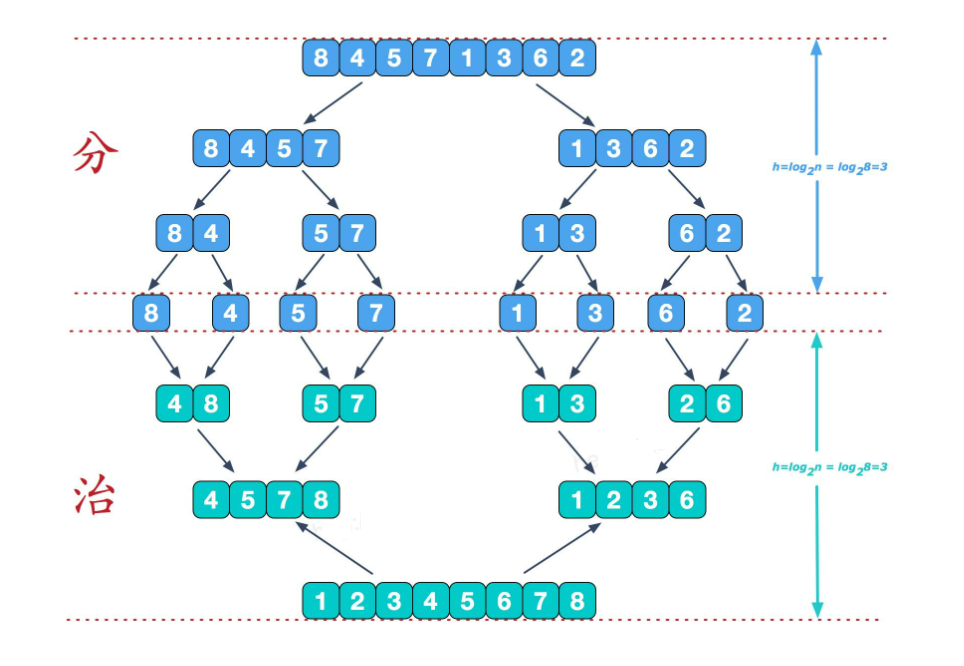
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
- 分解(Divide):将n个元素分成两个个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
代码实现
1. 递归版本
public static void mergeSort(int[] arr) {int len = arr.length;partition(arr, 0, len-1);}public static void partition(int[] arr, int left, int right) {if (left >= right) {return;}// 将区间分成左右两个部分, 并将两个部分分别排序int mid = ((right-left) >> 1) + left;partition(arr, left, mid);partition(arr, mid+1, right);// 将两部分合并int[] temp = new int[right-left+1];int index = 0;int index1 = left;int index2 = mid+1;while (index1 <= mid && index2 <= right) {if (arr[index1] < arr[index2]) {temp[index++] = arr[index1++];} else {temp[index++] = arr[index2++];}}while (index1 <= mid) {temp[index++] = arr[index1++];}while (index2 <= right) {temp[index++] = arr[index2++];}// 重新拷贝回去for (int i = 0; i < index; i++) {arr[left+i] = temp[i];}}
2. 非递归版本
public static void mergeSortNonR(int[] arr) {int len = arr.length;// i 表示的是, 左右区间中每个区间的元素个数for (int i = 1; i < len; i*=2) {// j 每次要跳过两个区间for (int j = 0; j < len; j += 2*i) {int left1 = j;int right1 = j + i - 1;int left2 = right1 + 1;int right2 = left2 + i - 1;// 修正一下 right1, right2, 因为可能 right1 和 right2 越界了if (right1 >= len) {right1 = len-1;}if (right2 >= len) {right2 = len - 1;}// 开始合并int[] temp = new int[2*i];int index = 0;while (left1 <= right1 && left2 <= right2) {if (arr[left1] <= arr[left2]) {temp[index++] = arr[left1++];} else {temp[index++] = arr[left2++];}}while (left1 <= right1) {temp[index++] = arr[left1++];}while (left2 <= right2) {temp[index++] = arr[left2++];}// 拷贝回去for (int k = 0; k < index; k++) {arr[j+k] = temp[k];}}}}
总结:
- 时间复杂度: O(N*logN)
- 空间复杂度: O(N)
- 是稳定排序
- 对数据不敏感: 不管数据原本怎么排列, 都需要先分解, 然后归并。
- 归并的缺点在于需要 O(N) 的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
海量数据的排序问题
假设条件为:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 2 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
以上就是对归并排序的讲解, 希望能帮到你 !
评论区欢迎指正 !
相关文章:

【算法】归并排序 详解
归并排序 详解 归并排序代码实现1. 递归版本2. 非递归版本 排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性: 假定在待排序的记录序列中,存在多个具有相…...

linux 进程隔离Namespace 学习
一、linux namespace 介绍 1.1、概念 Linux Namespace是Linux内核提供的一种机制,它用于隔离不同进程的资源视图,使得每个进程都拥有独立的资源空间,从而实现进程之间的隔离和资源管理。 Linux Namespace的设计目标是为了解决多个进程之间…...
【MySQL】事务 详解
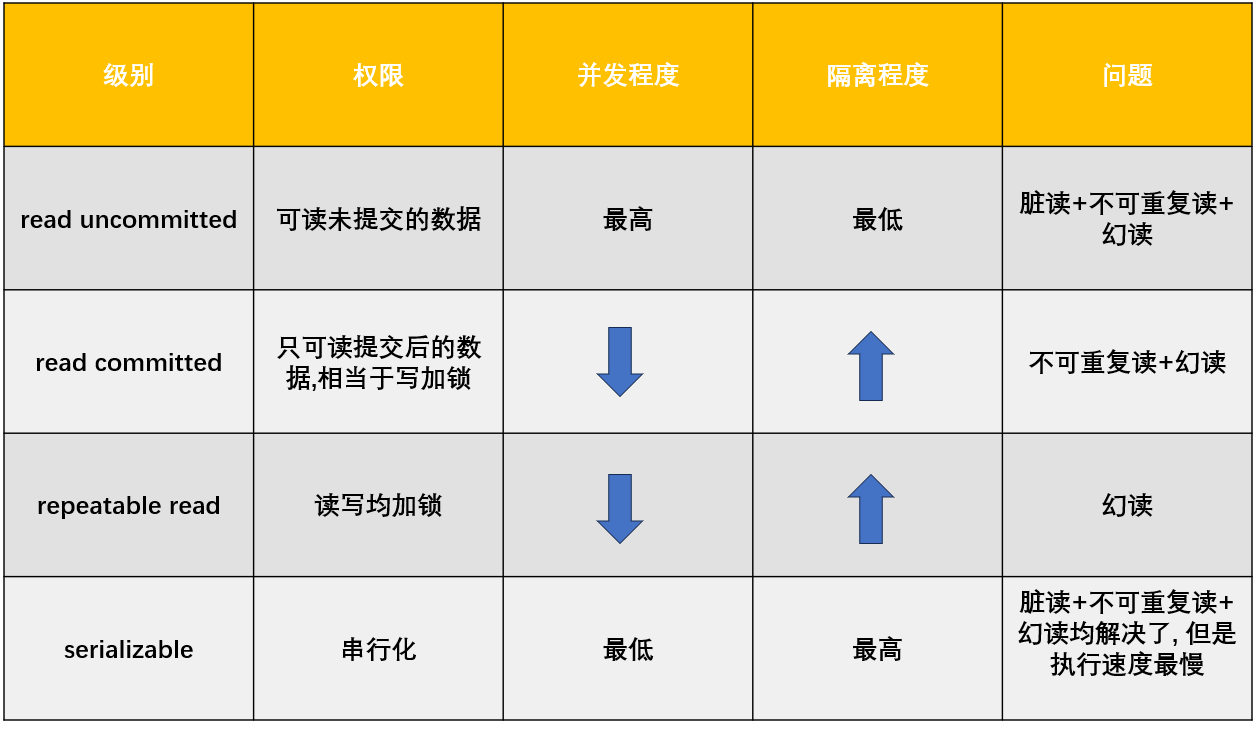
事务 详解 一. 为什么使用事务二. 事务的概念三. 使用四. 事务的特性原子性(Atomicity)一致性(Consistency)隔离性(Isolation)持久性(Durability) 五. 事务并发所带来的问题脏读问题…...

爬虫到底难在哪里?
目录 爬虫到底难在哪里 怎么学习爬虫 注意事项 爬虫工具 总结 学习Python爬虫的难易程度因人而异,对于具备编程基础的人来说,学习Python爬虫并不困难。Python语言本身比较简单易学,适合初学者使用。 爬虫到底难在哪里 爬虫的难点主要包…...

linux常用命令行整理
1、linux的以及目录 bin 二进制可执行文件sbin 二进制可执行文件(root用户权限)etc 系统管理和配置文件,例如常见host文件home 用户文件的根目录usr 用户存放系统应用程序(共享系统资源)opt 可选的应用程序proc 虚拟文件系统root 超级用户dev 存放设备文件mnt 系统管理员安装临…...

python字符串相关
python字符串相关 一、reverse() 函数 只能反转 列表二、reversed() 反转元组字符串等等 返回迭代器三、join和reversed反转字符串四、join串联字符串(join连接对象仅限字符串、储存字符串的元组、列表、字典)数字对象可通过str()转化为字符串⭐对象为字…...

JavaScript学习笔记01
JavaScript笔记01 什么是 JavaScript JavaScript 是一门世界上最流行的脚本语言,它是一种弱类型的脚本语言,其代码不需要经过编译,而是由浏览器解释运行,用于控制网页的行为。 发展历史 参考:JavaScript的起源故事…...
golang 通用的 grpc http 基础开发框架
go-moda golang 通用的 grpc http 基础开发框架仓库地址: https://github.com/webws/go-moda仓库一直在更新,欢迎大家吐槽和指点 特性 transport: 集成 http(echo、gin)和 grpc。tracing: openTelemetry 实现微务链路追踪pprof: 分析性能config: 通用…...
FSK解调技术的FPGA实现
本原创文章由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处 一、FSK信号的解调原理 FSK信号的解调也有非相干和相干两种,FSK信号可以看作是用两个频率源交替传输得到的,所以FSK的接收机由…...
Matlab图像处理-高斯低通滤波器
高通滤波 图像的边缘、细节主要位于高频部分,而图像的模糊是由于高频成分比较弱产生的。高通滤波就是为了高消除模糊,突出边缘。因此采用高通滤波器让高频成分通过,消除低频噪声成分削弱,再经傅里叶逆变换得到边缘锐化的图像。 …...
文件上传之图片马混淆绕过与条件竞争
一、图片马混淆绕过 1.上传gif imagecreatefromxxxx函数把图片内容打散,,但是不会影响图片正常显示 $is_upload false; $msg null; if (isset($_POST[submit])){// 获得上传文件的基本信息,文件名,类型,大小&…...

代码随想录二刷day16
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣104. 二叉树的最大深度二、力扣559. N 叉树的最大深度三、力扣111. 二叉树的最小深度三、力扣力扣222. 完全二叉树的节点个数 前言 一、力扣104. 二叉树…...

【开发】安防监控/视频存储/视频汇聚平台EasyCVR优化播放体验的小tips
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、H.265自动转码H.264、平台级联等。为了便于用户二次开发、调用与集成,…...
算法_C++—— 只出现一次的数字)
力扣(LeetCode)算法_C++—— 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。 示例 1 : 输入࿱…...
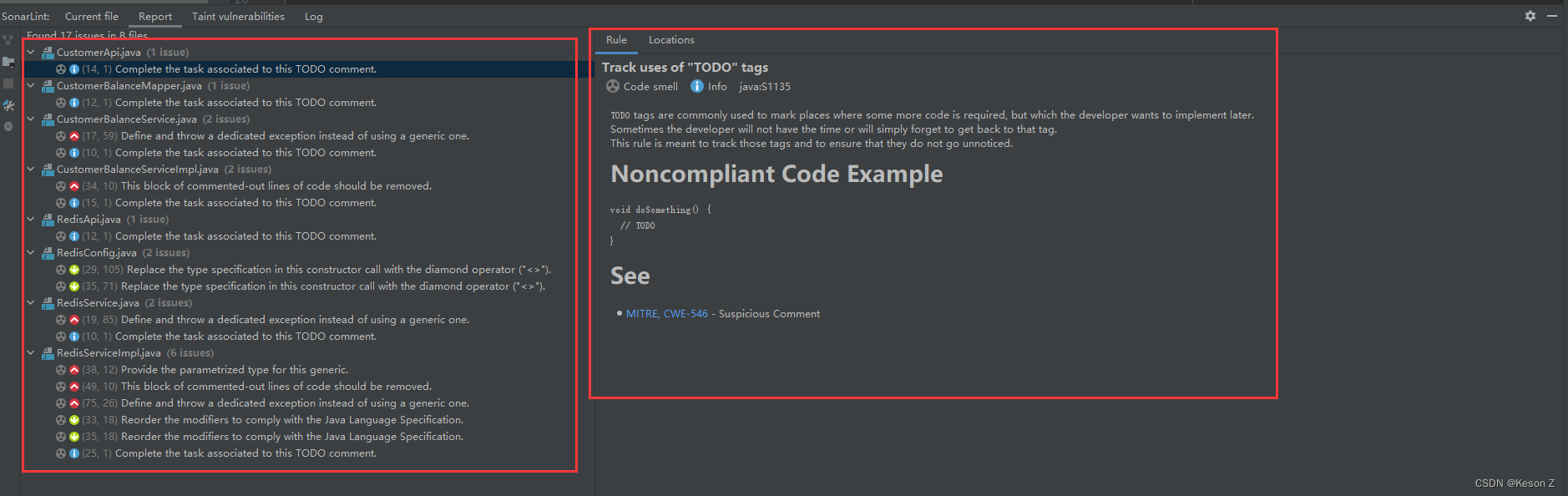
Windows配置SonarQube代码审查工具详细步骤(附带IDEA SonarLint插件使用)
文章目录 环境说明以及准备一. SonarQube的下载与安装二. 添加SonarQube项目三. 使用Maven命令上传代码到SonarQube四. IDEA安装SonarLint插件 环境说明以及准备 本篇博客使用的SonarQube版本为9.8,注意JDK 1.8已经不能支持 NameVersionDownLoad LinkSonarQube9.8…...

【Unity3D】UI Toolkit元素
1 前言 UI Toolkit简介 中介绍了 UI Builder、样式属性、UQuery、Debugger,UI Toolkit容器 中介绍了 VisualElement、ScrollView、ListView、GroupBox 等容器,UI Toolkit样式选择器 中介绍了简单选择器、复杂选择器、伪类选择器等样式选择器,…...
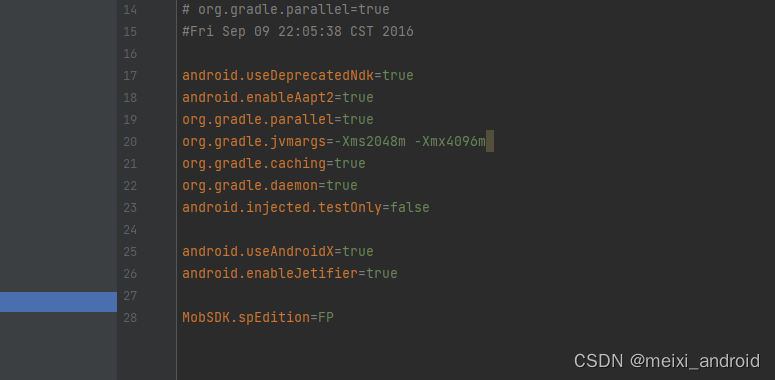
Task :app:compileDebugKotlin FAILED
gradle.properties 里面加上 android.enableJetifiertrue...

Android——数据存储(一)(二十一)
1. 数据存储 1.1 知识点 (1)掌握Android数据存储的分类; (2)可以使用SharedPreferences存储数据。 1.2 具体内容 对于我们数据的存储而言,Android一共提供了5个数据存储的方式:SharedPrefe…...

机器学习课后习题 ---数学基础回顾
(一)选择题 1.函数y=1/(x+1)是 A.偶函数 B.奇函数 C.单调函数 D.无界函数 2.设f(sin(x/2)=cosx+1,则f(x)为() A.2x-2 B.2-2x C.1+2 …...
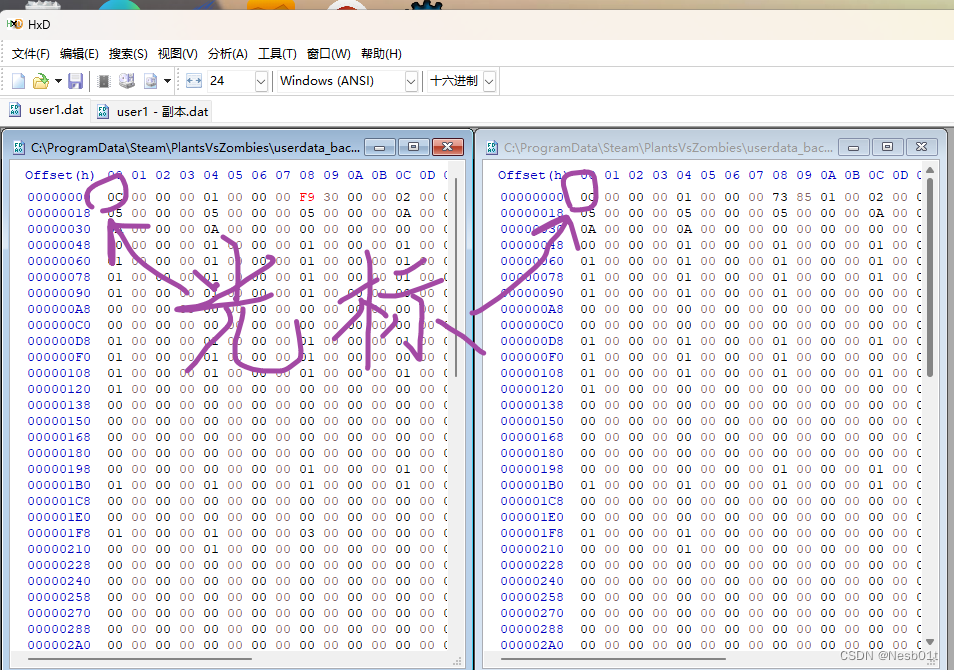
CS420 课程笔记 P4 - 以16进制形态编辑游戏文件
文章目录 IntroductionFinding save filesStringsUnicodeExample!Value searchHealth searchConclusion Introduction 这节课我们将学习编辑十六进制,主要用于编辑保存文件,但十六进制编辑涉及的技能可以很好地转移到: Save file editingRe…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
