【算法】堆排序 详解
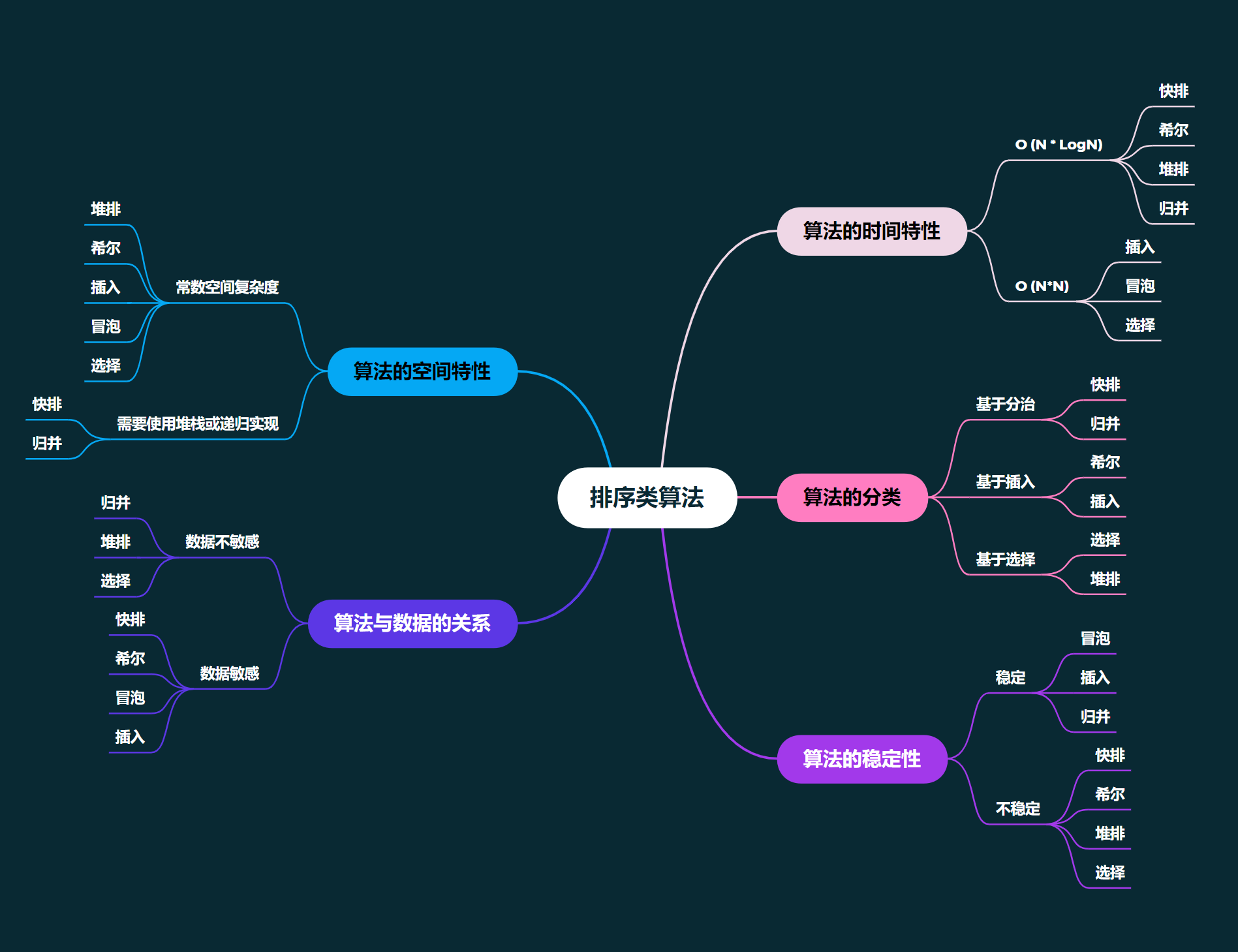
堆排序 详解
- 堆排序
- 代码实现
排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
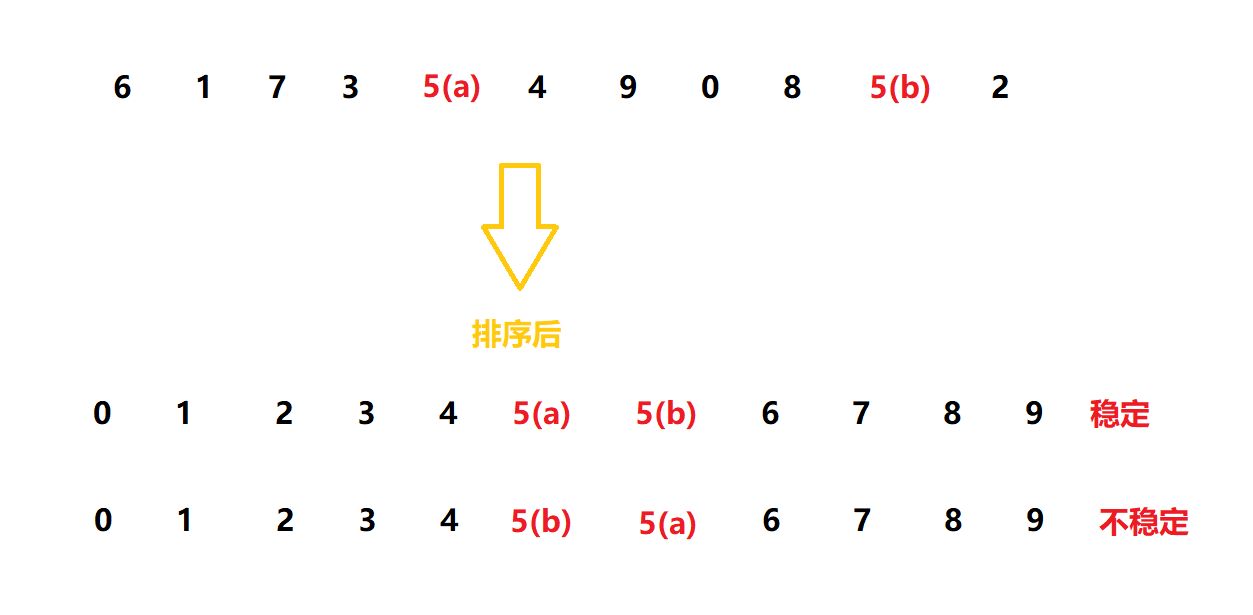
稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中, r[i] = r[j], 且 r[i] 在 r[j] 之前,而在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
(注意稳定排序可以实现为不稳定的形式, 而不稳定的排序实现不了稳定的形式)
内部排序: 数据元素全部放在内存中的排序。
外部排序: 数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
堆排序
堆排序 (Heapsort) 是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
为什么排升序建大堆?
- 因为假如排升序建小堆的话, 那么 我们只能得到最小的数字这一个, 同时堆的结构已经被破坏了, 因为我们直到最小值之后肯定要把这个最小值拿出来, 让剩下的元素进行排序, 也就是说堆的根节点下标要从 1 开始了, 这样就需要重新建堆了, 而建堆的时间复杂度是 O(N), 这样每选出来一个数, 就建一次堆, 总的时间复杂度就是 O(N*N) 了, 完全没有用上堆的优势。
- 但是假如排升序建大堆的话, 每次我们能选出来最大的值, 然后把它与最后位置的元素进行交换, 那么堆的根节点的位置还是从 0 开始,唯一可能不满足堆的性质情况就是 根节点小于 其他节点, 此时只需要 将根节点进行向下调整算法即可,不用重新建堆 。
友情链接:堆的讲解
基本思想: 建堆和排序。
- 建堆(Heapify):
- 首先,将待排序的数组视为一个完全二叉树。
- 从数组的最后一个非叶子节点开始,逐个向前处理,对每个节点执行向下调整算法(将较大的元素交换到子节点的位置),直至整个数组构建成一个最大堆(Max Heap)或最小堆(Min Heap)。
- 最大堆的特点是每个节点的值都大于或等于其子节点的值,最小堆则相反,每个节点的值都小于或等于其子节点的值。
- 排序:
- 一旦构建好堆,堆顶元素就是最大(最小)元素。
- 将堆顶元素与堆的最后一个元素交换位置,然后将堆的大小减 1。
- 对新的堆顶元素执行一次下沉操作,将新的最大(最小)元素浮到堆顶。
- 重复上述步骤,直到堆的大小为 1,排序完成。
堆排序的关键在于如何维护堆的性质,即使交换元素后,仍然保持堆的性质。这是通过向下调整操作来实现的,确保每次交换后最大(最小)元素移到堆的顶部。

代码实现
public static void heapSort(int[] arr) {int len = arr.length;// 排升序// 建大堆// 从最后一个非叶子节点进行向下调整for (int i = (len-1-1)/2; i >= 0; i--) {shiftDown(arr, i, len);}// 排序// 从最后一个节点开始与第一个节点交换位置for (int i = len-1; i > 0; i--) {// 最大值放到最后面swap(arr, 0, i);// 交换完成后重新调整堆, 注意 此时堆的大小要 - 1, 但是 这正好与 i 相同, 所以直接使用了 ishiftDown(arr, 0, i);}}/*** 向下调整算法*/public static void shiftDown(int[] arr, int index, int len) {int parent = index;int child = parent * 2 + 1;// 一直向下调整至符合堆 或者 至最后一个节点while (child < len) {if (child+1 < len && arr[child+1] > arr[child]) {child++;}if (arr[child] > arr[parent]) {// 交换节点swap(arr, parent, child);// 继续向下调整parent = child;child = parent * 2 + 1;} else {// 调整完成break;}}}
总结:
- 时间复杂度: O(N*logN)
- 空间复杂度: O(1)
- 是不稳定排序: 向下调整过程中, 可能相对顺序发生变化
- 对数据不敏感: 不管原本数据怎么分布, 都要先建堆, 然后排序
- 相对于快速排序和归并排序,堆排序通常效率较低,因为它的数据访问模式不够连续,可能导致缓存不命中
以上就是对堆排序的讲解, 希望能帮到你 !
评论区欢迎指正 !
相关文章:

【算法】堆排序 详解
堆排序 详解 堆排序代码实现 排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,…...

解决Maven依赖下载问题:从阿里云公共仓库入手
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【Java基础】学习笔记2 - 数组运算符与main方法
目录 多态数组运算符hashCodefinalize 方法 第三阶段类变量类方法main 方法代码块单例模式饥饿式懒汉式 多态数组 顾名思义,就是在一个数组内体现多态 public class PolyArrDemo {public static void main(String[] args) {// 定义多态数组Fruit[] fruits new Fr…...
stable diffusion实践操作-复制-清空-保存提示词
系列文章目录 stable diffusion实践操作 stable diffusion实践操作-webUI教程 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、右上生成图标附近按钮介绍1. 箭头介绍(复现别人的…...

【Spring 事务和事务传播机制】
目录 1 事务概述 1.1 为什么需要事务 1.2 事务的特性 1.3 Spring 中事务的实现 2 Spring 声明式事务 2.1 Transactional 2.2 Transactional 的作用范围 2.3 Transactional 的各种参数 2.3.1 ioslation 2.4 事务发生了异常,也不回滚的情况 异常被捕获时 3 事务的传…...
【爬虫】实验项目二:模拟登录和数据持久化
目录 一、实验目的 二、实验预习提示 三、实验内容 实验要求 基本要求: 改进要求A: 改进要求B: 四、实验过程 基本要求: 源码如下: 改进要求A: 源码如下: 改进要求B: 源码如下&…...
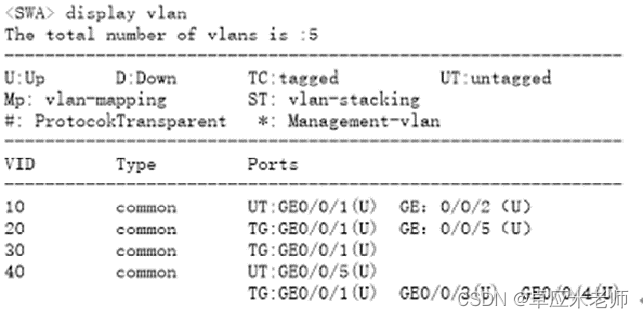
图文版:以太网二层接口类型(含配套习题)
常见的以太网二层接口类型包括以下三种: 一、Access接口 access链路类型端口,一种交换机的主干道模式,2台交换机的2个端口之间是否能够建立干道连接,取决于这2个端口模式的组合。 Access端口在收到以太网帧后打开VLAN标签&#…...
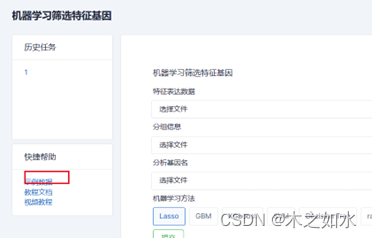
生信豆芽菜-机器学习筛选特征基因
网址:http://www.sxdyc.com/mlscreenfeature 一、使用方法 1、准备数据 第一个文件:特征表达数据 第二个文件:分组信息,第一列为样本名,第二列为患者分组 第三个文件:分析基因名 2、选择机器学习的方…...
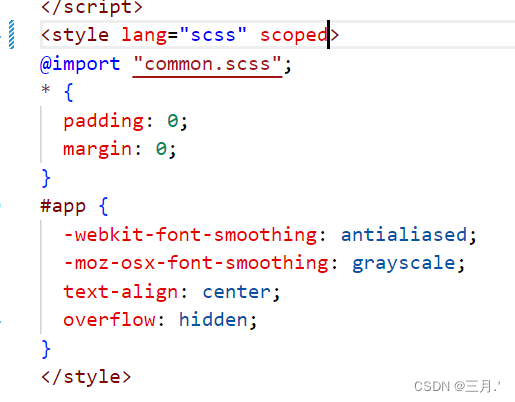
v-html富文本里面的图片设置宽高不起作用的原因
把scoped去掉...
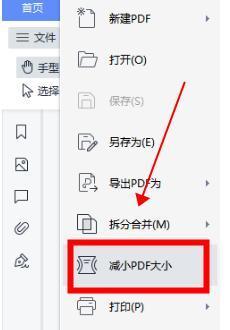
pdf文档怎么压缩小一点?文件方法在这里
在日常工作和生活中,我们经常会遇到需要上传或者发送pdf文档的情况。但是,有时候pdf文档的大小超出了限制,需要我们对其进行压缩。那么,如何将pdf文档压缩得更小一点呢?下面,我将介绍三种方法,让…...
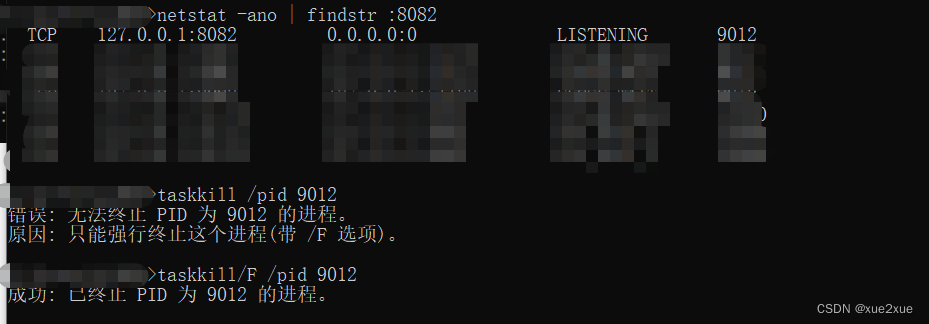
CMD关闭占用端口
1. netstat -ano | findstr :xxxx 2. taskkill /pid xxxx 3. 强制关闭taskkill/F /pid xxxx...
复制粘贴是怎么实现的
在上面的代码中,command 和 select 是自定义的函数。它们的作用如下: 实现复制粘贴的思路: 创建一个 textarea 标签将 textarea 移出可视区域给这个 textarea 赋值将这个 textarea 标签添加到页面中调用 textarea 的 select 方法调用 docum…...
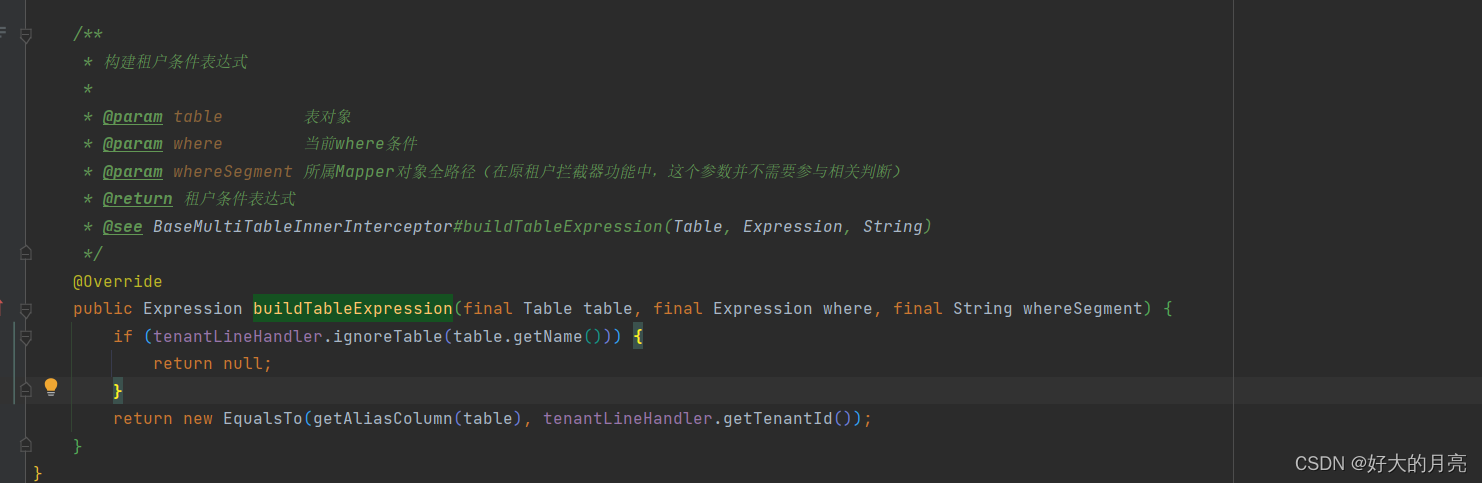
mybatisplus多租户原理略解
概述 当前mybatisPlus版本 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.3.2</version> </dependency>jdk版本:17 springboot版本:…...

Spring整合RabbitMQ-配制文件方式-1-消息生产者
Spring-amqp是对AMQP的一些概念的一些抽象,Spring-rabbit是对RabbitMQ操作的封装实现。 主要有几个核心类RabbitAdmin、RabbitTemplate、SimpleMessageListenerContainer等 RabbitAdmin类完成对Exchange、Queue、Binding的操作,在容器中管理 了RabbitA…...
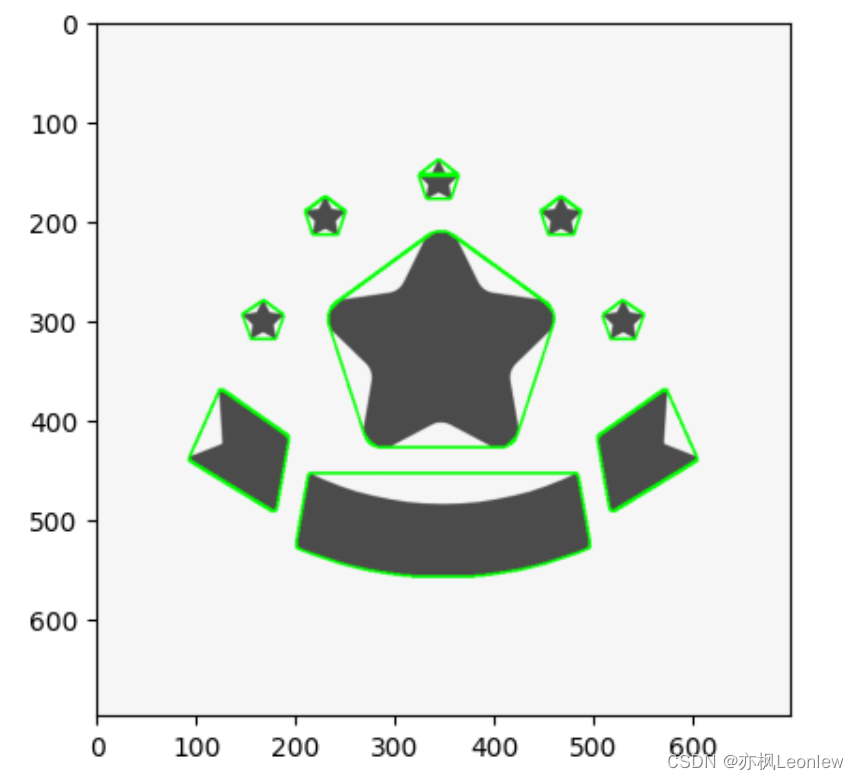
Python Opencv实践 - 凸包检测(ConvexHull)
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/stars.png") plt.imshow(img[:,:,::-1])img_contour img.copy() #得到灰度图做Canny边缘检测 img_gray cv.cvtColor(img_contour, cv.COLOR_BGR2GRAY) edges…...

IP网络广播系统有哪些优点
IP网络广播系统有哪些优点 IP网络广播系统有哪些优点? IP网络广播系统是基于 TCP/IP 协议的公共广播系统,采用 IP 局域网或 广域网作为数据传输平台,扩展了公共广播系统的应用范围。随着局域网络和 网络的发展 , 使网络广播的普及变为可能 …...

【LeetCode】83. 删除排序链表中的重复元素
83. 删除排序链表中的重复元素(简单) 方法:一次遍历 思路 由于给定的链表是排好序的,因此重复的元素在链表中出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。 从指针 cur 指…...
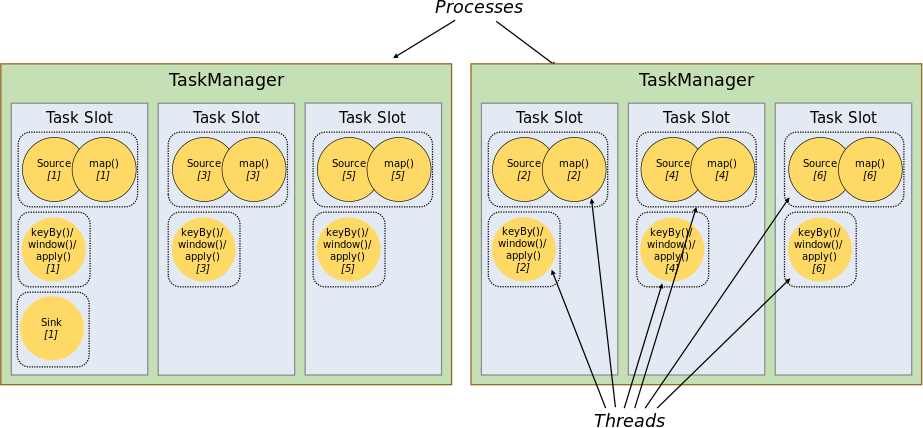
【大数据】Flink 详解(七):源码篇 Ⅱ
本系列包含: 【大数据】Flink 详解(一):基础篇【大数据】Flink 详解(二):核心篇 Ⅰ【大数据】Flink 详解(三):核心篇 Ⅱ【大数据】Flink 详解(四…...

stable diffusion实践操作-SD原理
系列文章目录 本文专门开一节写SD原理相关的内容,在看之前,可以同步关注: stable diffusion实践操作 文章目录 系列文章目录前言一、原理说明1.1、出图原理1.1.1 AI画画不是和人一样,从0开始,而是一个去噪点的过程&am…...

C++ Primer Plus第十三章编程练习答案
1,以下面的类声明为基础: // base class class Cd{ // represents a CD disk private: char performers[50] ; char label[20]; int selections;// number of selections double playtime; // playing time in minutes public: Cd(char * sl,char * s2,int n,double…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
