LRU算法 vs Redis近似LRU算法
LRU(Least Recently Use)算法,是用来判断一批数据中,最近最少使用算法。它底层数据结构由Hash和链表结合实现,使用Hash是为了保障查询效率为O(1),使用链表保障删除元素效率为O(1)。
LRU算法是用来判断最近最少使用到元素,常被用在缓存中数据清理、内存淘汰相关的场景,它底层是由Hash表和双向链表构成,Hash主要用来存储key和指向链表节点的指针,双向链表就是用来实现最近最少使用算法的数据结构,新访问的元素会加入到头部或者尾部(就看最终从哪个反向取了,我们这里定为头部),如果是已经访问的元素,并不会新添加到链表中,而是将链表中原来存在的这个节点移动到头部,最终链表中越靠近尾部的元素,代表最近最少使用的元素。
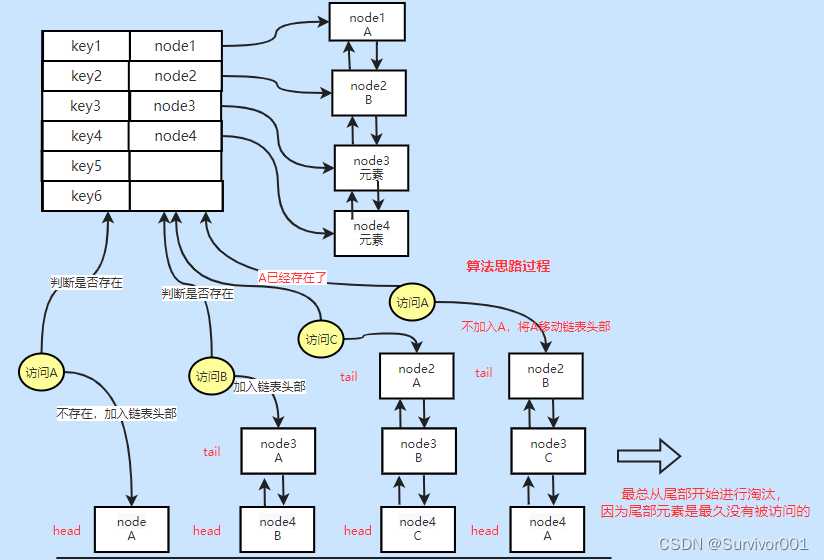
为什么要额外组合使用Hash和链表?单个数据结构也能完成不是吗?
为了提交效能,Hash的优势是查找元素为O(1),但是移动元素是O(n),链表查找元素复杂度是O(n),但是移动元素复杂度是O(1),所以为了提高效率,结构两种数据结构各自的优势,利用Hash的O(1),来查找元素是否存在,利用链表的O(1)来移动元素位置。
Redis近似LRU算法
什么是Redis近似LRU算法,为什么Redis不直接使用LRU算法?
近似LRU算法是Redis采用LRU算法思想,实现一个近似LRU的算法,在原LRU算法中需要维护一个Hash和链表,而Redis本身可以理解为一个大的字典,那就需要额外的去维护一个链表数据结构,Redis本身就是要经受大量数据的冲击的,所以这个链表将会占用更大的内存。Redis的宗旨就是高效,所以它没有使用这样的一个链表。它的做法如下:

Redis最开始的做法:
1、当设置了LRU回收策略之后,对元素进行访问时,会调用一次server.lruclock方法,获取Redis时钟时间戳(redis时钟默认1毫秒更新一次)并进行取模(防止时间戳递增,最后超过了24bit),记录在元素value中lru属性中。
2、当内存达到maxmemory时,会随机抽取5(可以通过maxmemory-policy设定)个样本key进行时间戳判断,淘汰时间戳最小的(也就是最久远的一个key)
优点:不用额外的维护一个链表,节省了内存,同时随机采样淘汰方式也避免了大数据量key遍历处理的耗时。
缺点:因为是随机采样删除,所以会出现更早key迟迟没有被采样删除的情况。钉子户。
Redis3.0 做了LRU算法升级
Redis在3.0之后对LRU算法做了升级,加入了候选池Pool(16字节),首次抽样5个会放入都Pool中,并按照时间大小lru排序,后续每次选取的Key的lru必须要小于pool的最小值(也就是key要比pool中的更早),才放入pool中,直到pool满,当有新元素加入时,只需要将pool中最万的key(也就是最大的)删除即可。
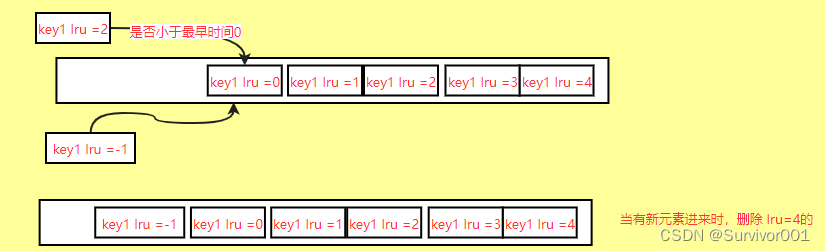
升级之后的算法,可以更大密度的将更久没有使用的key删除,减少了钉子户的存在。
RedisLFU算法
在Redis4.0 推出了LFU算法,这个是基于访问次数维护的回收算法,算法和LRU差不多,就是在lru中加入了请求次数的计数count维护。从时间和频次两个维度来计算key的热度。他的好处是,如果一个key很就没有被访问到,突然最近被访问了一次,在LRU算法中,它是不容易被淘汰的,但是在LRF算法中,会统计它访问频次,发现不足定位很热的key,所以还是会被删除。所以LFU算法很适合用于热点数据的删除策略。
相关文章:

LRU算法 vs Redis近似LRU算法
LRU(Least Recently Use)算法,是用来判断一批数据中,最近最少使用算法。它底层数据结构由Hash和链表结合实现,使用Hash是为了保障查询效率为O(1),使用链表保障删除元素效率为O(1)。 LRU算法是用来判断最近最少使用到元素…...
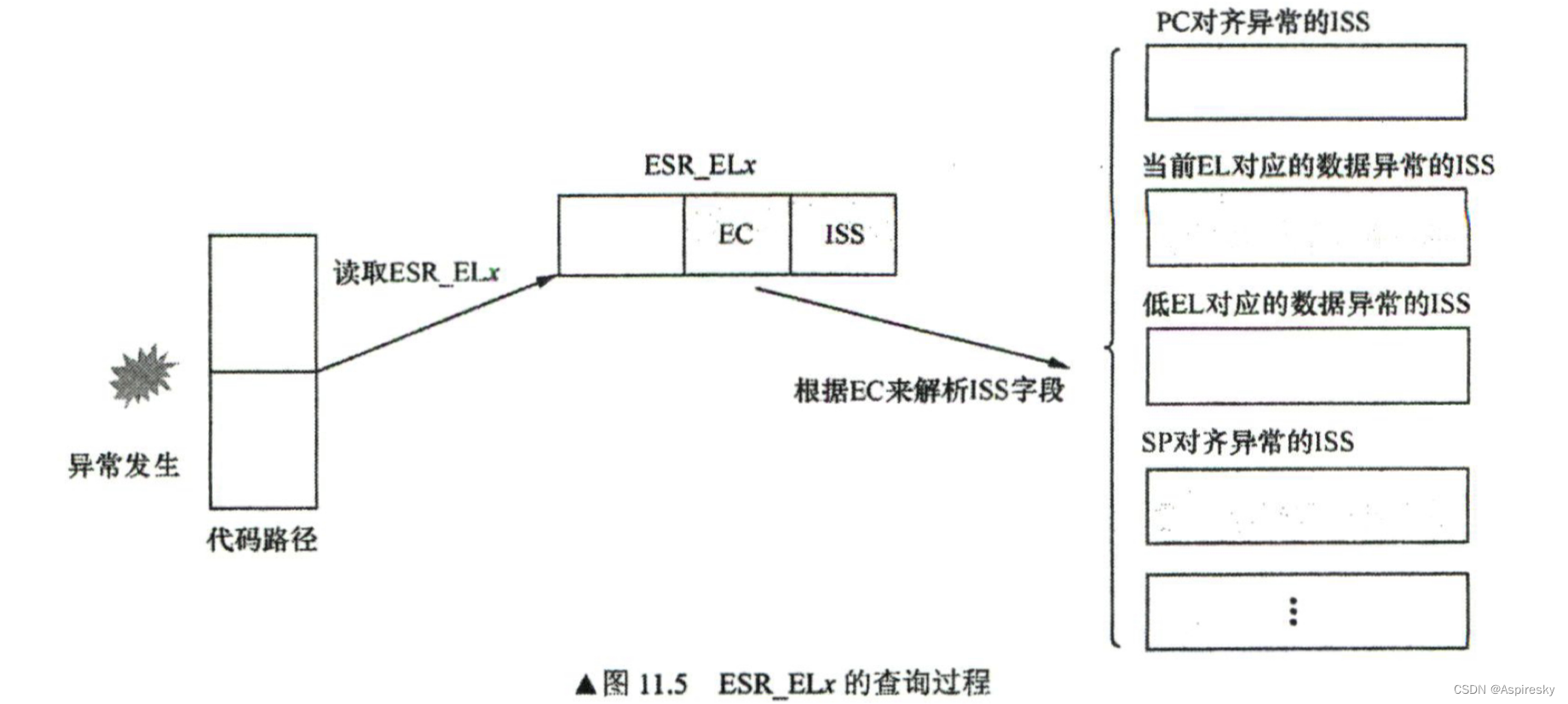
浅析ARMv8体系结构:异常处理机制
文章目录 概述异常类型中断终止Abort复位Reset系统调用 异常处理流程异常入口异常返回异常返回地址 堆栈选择 异常向量表异常向量表的配置 同步异常解析相关参考 概述 异常处理指的是处理器在运行过程中发生了外部事件,导致处理器需要中断当前执行流程转而去处理异…...

Golang开发--Goroutine的使用
Go 语言天生支持并发编程,提供了丰富的原语和工具来编写并发程序。Goroutine 是 Go 语言中的轻量级执行单位。它们是由 Go 运行时(runtime)管理的,并且能够在单个线程上运行成千上万个 Goroutine。创建 Goroutine 非常高效&#x…...

【Linux】package ‘python-yaml‘ has no installation candidate 如何解决
要解决此问题,可以尝试以下几个步骤: 确保系统已经更新到最新版本。可以使用以下命令进行系统更新: sudo apt update sudo apt upgrade确保您的软件源列表中包含了正确的软件源。可以使用以下命令编辑软件源列表: sudo nano /etc/…...

Selector选择器在AspNetCore中的用法
Selector选择器在AspNetCore中的用法 背景 项目编辑过程中会选择其所属的上级项目,而上级项目在数据结构中是以ParentID的方式表达,而非Project类型,用户不会记录也不应该记录ID值,因此应提供Selector项目下拉框供用户选择。 但…...
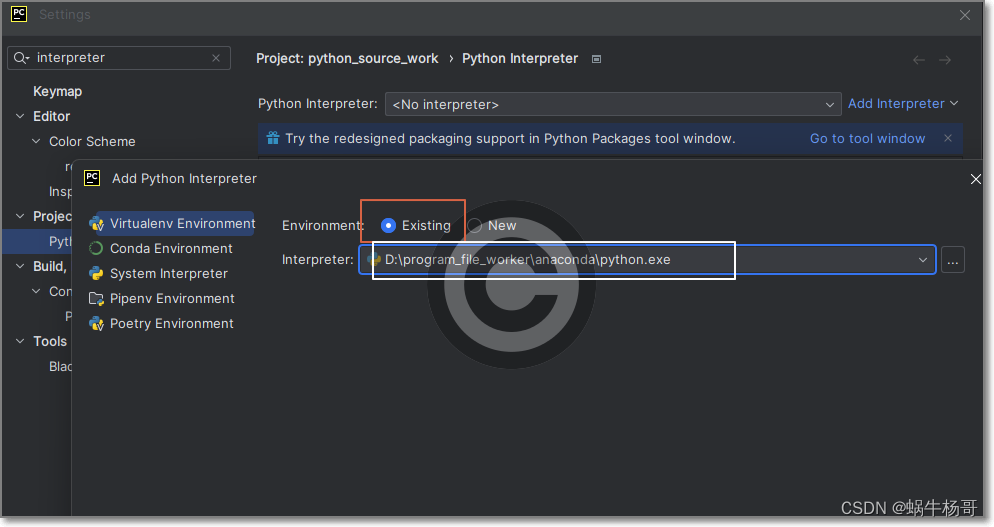
anaconda3最新版安装|使用详情|Error: Please select a valid Python interpreter
Win11查看安装的Python路径及安装的库 anaconda3最新版安装|使用详情|Error: Please select a valid Python interpreter 介绍开源包管理系统和环境管理系统 ,包括多种语言的包安装,运行,更新,删除,最重要的是可以解…...

java八股文面试[多线程]——锁的分类
1.1 可重入锁、不可重入锁 Java中提供的synchronized,ReentrantLock,ReentrantReadWriteLock都是可重入锁。 重入:当前线程获取到A锁,在获取之后尝试再次获取A锁是可以直接拿到的。 不可重入:当前线程获取到A锁&…...

儿童安全门和围栏,以及游戏围栏等美国站要求的合规标准是什么?
儿童安全门和围栏 儿童安全门和围栏用于在门口(如门道)内设置围栏,或用作自支撑围栏,将幼儿可能在其中活动的区域围起来。这些商品可能由塑料、金属、乙烯树脂或木制组件等材料制成。此政策包括但不限于可扩展围栏、伸缩安全门和…...

kafka配合ElasticStack技术栈的搭配使用
今日内容: - kafka生产环境调优; - kafka配合ElasticStack技术栈的搭配使用; - zookeeper集群部署; - zookeeper的ACL; - zookeeper的调优; - PB级别项目; - ES8集群搭建/elk; (待定...) 订阅1个的topic: 老男孩: 10 多个不同的主题…...
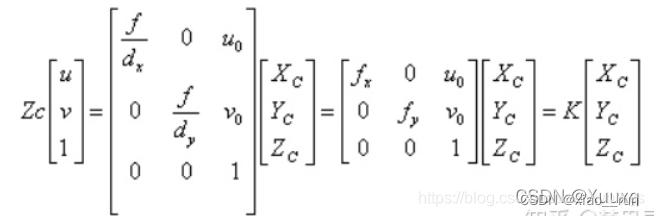
对极几何与三角化求3D空间坐标
一,使用对极几何约束求R,T 第一步:特征匹配。提取出有效的匹配点 void find_feature_matches(const Mat &img_1, const Mat &img_2,std::vector<KeyPoint> &keypoints_1,std::vector<KeyPoint> &keypoints_2,std::vector&l…...

英语语法笔记
1.英语五大句型 主谓(主语动词) 主谓宾(主语动词宾语) 主谓宾宾(主语动词简接宾语直接宾语) 主谓宾补(主语动词宾语宾语补语) 主系表(主语系动词主语补语) 1…...
ES6的面向对象编程以及ES6中的类和对象
一、面向对象 1、面向对象 (1)是一种开发思想,并不是具体的一种技术 (2)一切事物均为对象,在项目中主要是对象的分工协作 2、对象的特征 (1)对象是属性和行为的结合体 &#x…...

ConfigMaps in K8s
摘要 ConfigMaps是Kubernetes(K8s)中用于存储应用程序配置信息的一种资源对象。它将key-value对存储为Kubernetes集群中的一个资源,并可以在Pod中以卷或环境变量的形式使用。 ConfigMaps的设计目的是将应用程序配置与应用程序本身解耦。它可…...

《机器人学一(Robotics(1))》_台大林沛群 第 6 周 【轨迹规划_直线转折处抛物线平滑】Quiz 6
步骤: 1、 编程 将PPT 的例子 跑一遍, 确保代码无误 2、根据题目 修改 相关参数 文章目录 求解代码_Python 解决的问题: 线段间转折点 的 速度 不连续 解决方法: 将直线段 两端 修正为 二次方程式 二次项圆滑 求解代码_Python …...
关于vscode的GitLens插件里的FILE HISTORY理解
最近在用vscode的GitLens插件开发项目遇到这个疑问,先看图: 每当我点击FILE HISTORY 一个commit时,正常来说显示器会自动将点击的提交版本和它上一个提交版本进行比较,如果单纯这么理解的话就错了,因为GitLens的File …...
通过idea实现springboot集成mybatys
概述 使用springboot 集成 mybatys后,通过http请求接口,使得通过http请求可以直接直接操作数据库; 完成后端功能框架;前端是准备上小程序,调用https的请求接口用。简单实现后端框架; 详细 springboot 集…...
算法_C++——移位字符串分组)
力扣(LeetCode)算法_C++——移位字符串分组
给定一个字符串,对该字符串可以进行 “移位” 的操作,也就是将字符串中每个字母都变为其在字母表中后续的字母,比如:“abc” -> “bcd”。这样,我们可以持续进行 “移位” 操作,从而生成如下移位序列&am…...

Vue2 与Vue3的区别?面试题
Vue 2和Vue 3是Vue.js框架的不同版本,在面试中经常涉及到它们之间的区别。以下是Vue 2和Vue 3的主要区别: 性能提升:Vue 3在性能方面进行了优化。Vue 3引入了更高效的Diff算法,提高了渲染性能。此外,Vue 3还进行了代码…...

java代码:Random和Scanner应用的小例子-猜数字小游戏
//java代码:Random和Scanner应用的小例子-猜数字小游戏 package com.test; import java.util.Random; import java.util.Scanner; /* * 需求:猜数字小游戏。 * 系统产生一个1-100之间的随机数,请猜出这个数据是多少? * * 分析…...
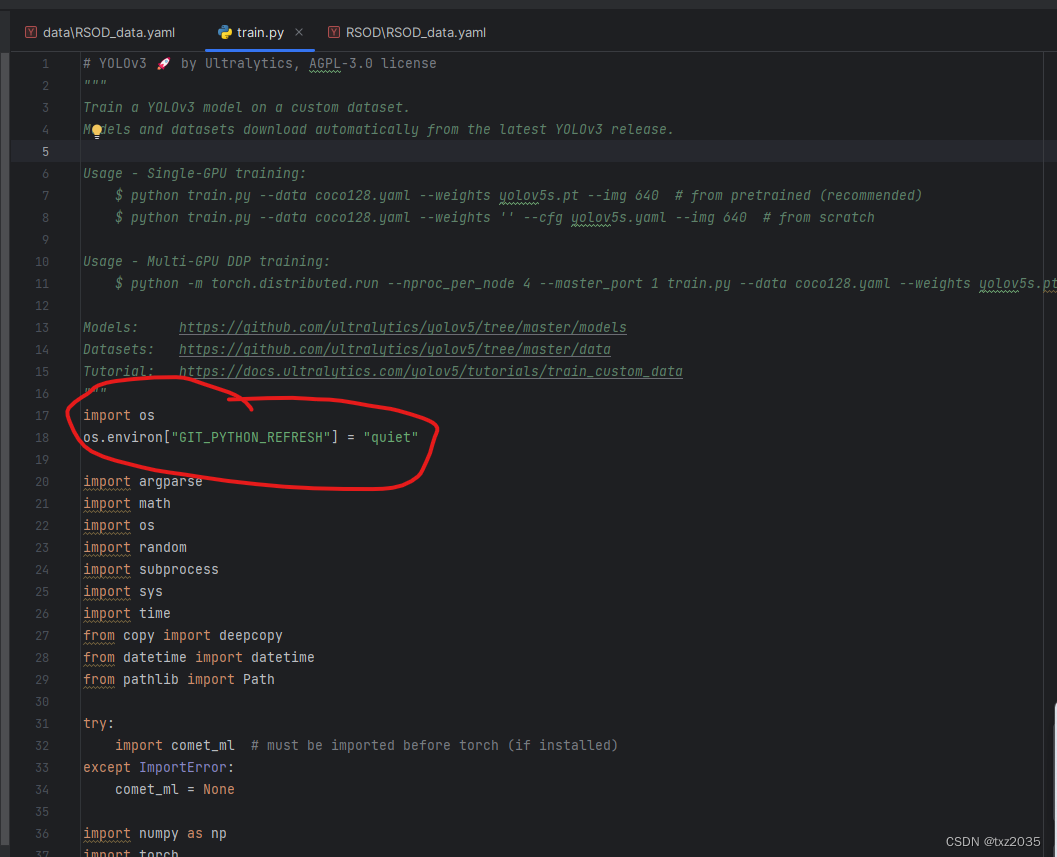
python调用git出错:ImportError: Failed to initialize: Bad git executable.
报错信息 #报错信息 Traceback (most recent call last): File “”, line 1, in File “C:\Python27\lib\site-packages\git_init_.py”, line 85, in raise ImportError(‘Failed to initialize: {0}’.format(exc)) ImportError: Failed to initialize: Bad git executab…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
