算法设计与分析 | 最多约数
题目:
正整数x的约数是能整除x的正整数。正整数x 的约数个数记为div(x)。例如,1,2,5,10 都是正整数10 的约数,且div(10)=4。设a 和b 是2 个正整数,a≤b,找出a和b之间约数个数最多的数x。
输入
对于给定的2个正整数a≤b。
输出
编程计算a 和 b 之间约数个数最多的数的数量,和约数最多的数。
分析
可以写一个统计约数个数的方法div(),然后在main里面写一个for循环,找出约数个数最多的数。
代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
//最多约数
int div(int n){int count = 0;//统计约数个数for (int i = 1; i <= n; i++) {if (n % i == 0) {count++;}}return count;
}
int main() {int first, end;//区间数scanf("%d %d", &first, &end);int max = 0, maxNum = 0;for (int j = first; j <= end; j++) {int temp = div(j);if (temp > max) {//如果约数个数比max大,则将该数赋给max,并记录下该约数最多的数max = temp;maxNum = j;}}printf("%d %d", max, maxNum);return 0;
}相关文章:

算法设计与分析 | 最多约数
题目: 正整数x的约数是能整除x的正整数。正整数x 的约数个数记为div(x)。例如,1,2,5,10 都是正整数10 的约数,且div(10)4。设a 和b 是2 个正整数,a≤b,找出a和b之间约数个数最多的数…...

MySQL 数据库常用操作语句的总结
1、创建数据库: CREATE DATABASE database_name;2、删除数据库: DROP DATABASE database_name;3、选择数据库: USE database_name;4、创建表: CREATE TABLE table_name (column1 datatype [condition],column2 datatype [cond…...

【面试经典150题】H 指数
题目链接 给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。 根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她&#x…...
ARM DIY(十)LRADC 按键
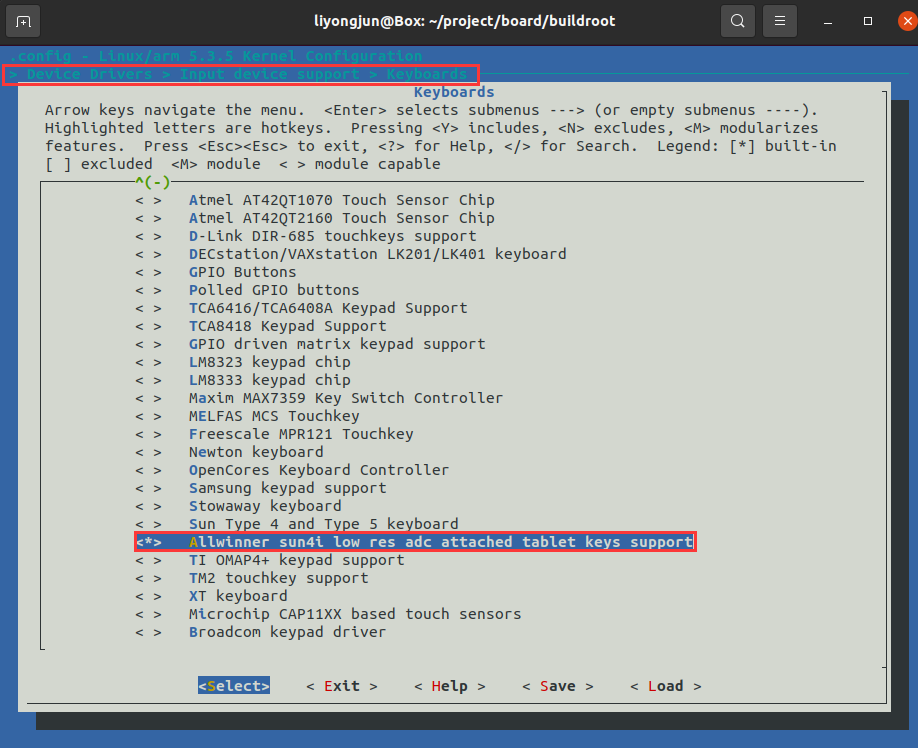
前言 ARM SOC 有别于单片机 MCU 的一点就是,ARM SOC 的 GPIO 比较少,基本上引脚都有专用的功能,因为它很少去接矩阵键盘、众多继电器、众多 LED。 但有时 ARM SOC 又需要三五个按键,这时候 LRADC 就是一个不错的选择,…...
每日一练 | 网络工程师软考真题Day31
阅读以下说明,答复以下【问题1】至【问题7】 【说明】 某网络拓扑结构如图3-1所示。网络A中的DNS_Server1和网络B中的DNS_Server2分别安装有Windows Server 2003并启用了DNS效劳。DNS_Server1中安装有IIS6.0,建立了一个域名为 abc 的Web站点。 图3-1 【…...
)
最优化:建模、算法与理论(优化建模——2)
3.10 K-均值聚类 聚类分析是 统计学中的一个基本问题,其在机器学习,数据挖掘,模式识别和图像分析中有着重要应用。聚类不同于分类,在聚类问题中我们仅仅知道数据点本身,而不知道每个数据点具体的标签。聚类分析的任务…...

库的相关操作
目录 一、创建数据库 1,创建数据库规则 2、创建案例 二、字符集和校验规则 1、查看系统默认字符集以及校验规则 2、查看数据库支持的字符集以及校验规则 3、校验规则对数据库的影响 三、操纵数据库 1、查看数据库和目前所在数据库 2、显示创建语句 3、修改数据库 4、…...

程序分区:全局区、常量区、栈区、堆区、代码区
#include <iostream> using namespace std; //全局变量 int g_a 10; int g_b 10; //全局常量 const int c_g_a 10; const int c_g_b 10;int main() { //局部变量 int a 10; int b 10; //打印地址 cout << "局部变量a地址为: " <…...

Jtti:windows虚拟机如何设定永久静态路由
在Windows虚拟机上设置永久静态路由需要使用命令行工具,具体步骤如下: 打开命令提示符: 在Windows虚拟机中,按下Win R组合键,输入"cmd"并按回车键,以打开命令提示符。 查看当前路由表࿱…...
之事务消息)
RocketMQ(3)之事务消息
一、发送事务消息案例 事务消息共有三种状态,提交状态、回滚状态、中间状态: TransactionStatus.CommitTransaction: 提交事务,它允许消费者消费此消息。TransactionStatus.RollbackTransaction: 回滚事务,它代表该消息将被删除…...
基于多设计模式下的同步异步日志系统
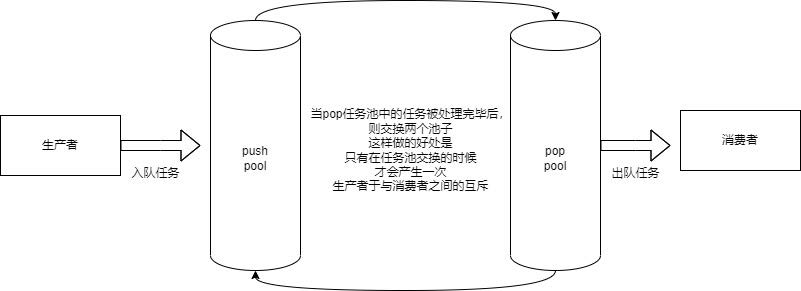
基于多设计模式下的同步&异步日志系统 代码链接:https://github.com/Janonez/Log_System 1. 项目介绍 本项目主要实现一个日志系统, 其主要支持以下功能: 支持多级别日志消息支持同步日志和异步日志支持可靠写入日志到标准输出、文件…...
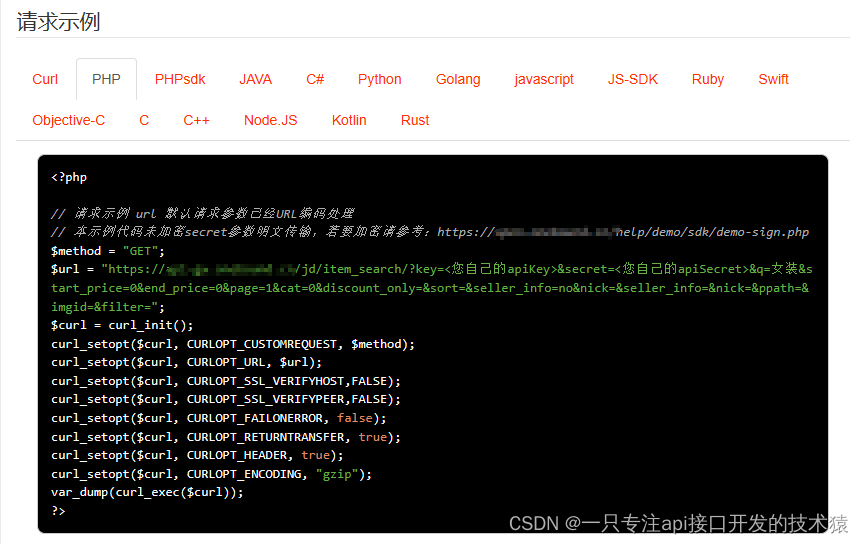
API接口与电商平台之间的联系,采集京东平台数据按关键字搜索商品接口示例
关键字搜索商品的重要性: 1.引入精准流量 关键词第一个也是最重要的作用就是为我们宝贝引进精准的流量,这一作用无论是在自然搜索中还是直通车中都是一样的。 第一步关乎的是我们宝贝的展现,而第二步用户是否会点进我们的宝贝,…...

代码随想录day41|343. 整数拆分96. 不同的二叉搜索树
343. 整数拆分 class Solution:def integerBreak(self, n: int) -> int:dp [0] *(n1)dp[2]1if n <3:return dp[n]for i in range(3,n1):for j in range(1,n):dp[i]max(j*(i-j),j*dp[i-j],dp[i])return dp[n] 96. 不同的二叉搜索树 class Solution:def numTrees(self, …...

Less常用内置函数
1,类型函数 isnumber(value) - 判断是否为数字isstring(value) - 判断是否为字符串isurl(value) - 判断是否为urliscolor(value) - 判断是否为颜色isunit(value, unit) - 判断value值是否为指定单位 示例: isnumber(12); // true isnumber(#333); // f…...
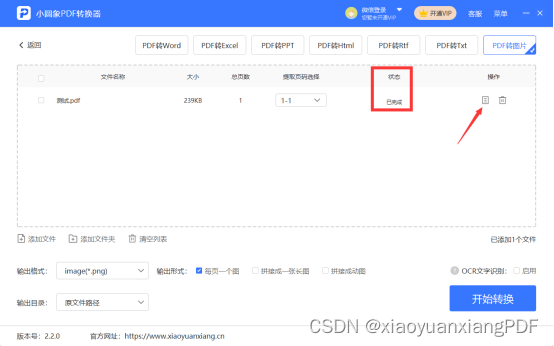
pdf转换成图片转换器在线怎么转?pdf转换成图片具体方法介绍
很多用户们都是比较喜欢使用pdf文档的,由于这种文件格式的便携性非常高,所以广泛的应用于工作和学习领域,再加上pdf文档可以随意转换成为其他的文件格式,更是让pdf文档受到了更多用户们的欢迎,那么pdf转换成图片转换器…...

JavaScript动态设置浏览器可视区域元素的文字颜色、监听滚动条、querySelectorAll、getBoundingClientRect
文章目录 前言htmlJavaScriptquerySelectorAllgetBoundingClientRect 前言 当元素出现在浏览器可视区域时给元素设置颜色等其他操作,比如当元素进入浏览器可视区域时,设置元素进入动画。 html <div id"idBox" class"box"><…...
意向客户的信息获取到底是怎样的,快来get一下
客户信息获取技术真的可以为企业提供精准客源吗?这个渠道到底安不安全,技术到底成不成熟?效果到底如何?下面简单的和大家分析一下。 客户信息获取技术是怎样的 手机采集引流方面,上量不精准,精准不上量的说…...

自动化测试常用脚本语言有哪些?
在自动化测试中,常用的脚本语言包括: 1. Python:Python是一个简洁、易读且功能强大的脚本语言,广泛应用于自动化测试领域。它具有丰富的测试框架和库,可以用于Web、移动应用和API等各种类型的测试。 2. Java࿱…...

mapreduce 的工作原理以及 hdfs 上传文件的流程
推荐两篇博文 mapreduce 的工作原理: 图文详解 MapReduce 工作流程_mapreduce工作流程_Shockang的博客-CSDN博客 hdfs 上传文件的流程 HDFS原理 - 知乎...

Ubuntu22.04安装ROS2
Ubuntu22.04安装ROS2 Excerpt ROS2官方文档 ROS2清华镜像站sudo apt update sudo apt upgrade locale # check for UTF-8 sudo apt update && sudo apt install locales sudo locale-gen en_US en_US.UTF-8 sudo update-locale LC_ALLe… ROS2官方文档 ROS2清华镜像站…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
