【向量数据库】相似向量检索Faiss数据库的安装及余弦相似度计算(C++)
目录
- 简介
- 安装方法
- 安装OpenBLAS
- 安装lapack
- 编译Faiss
- 代码示例
- 余弦相似度计算
- 输出ID号而非索引的改进版
简介
Faiss 是一个强大的向量相似度搜索库,具有以下优点:
-
高效的搜索性能:Faiss 在处理大规模向量数据时表现出色。它利用了高度优化的索引结构和近似搜索算法,可以快速地执行最近邻搜索和相似度匹配,具有很低的查询延迟。
-
高度可扩展:Faiss 提供了多种索引结构和算法的选择,包括 k-d树、IVF(Inverted File System)和 PQ(Product Quantization)等。这些索引结构能够轻松应对大规模的向量数据集,并支持高效的并行计算和分布式处理。
-
高精度的近似搜索:Faiss 通过采用近似搜索技术,在保证搜索速度的同时,尽量接近精确搜索的结果。这使得 Faiss 在许多实际应用中能够有效地处理高维度的向量数据,如图像、文本和推荐系统等。
-
多语言支持:Faiss 提供了多种编程语言的接口,如 Python、Java 和 Go 等,使得它能够方便地集成到各种应用和平台中。
然而,Faiss 也有一些局限性和缺点:
-
内存消耗:Faiss 在处理大规模向量数据时可能需要大量的内存。特别是在使用一些高级索引结构和算法时,内存消耗可能会很高。
-
学习曲线陡峭:对于初次接触 Faiss 的开发者来说,学习曲线可能会比较陡峭。理解并配置 Faiss 的索引结构、算法和参数可能需要一定的时间和经验。
综上所述,Faiss 是一个强大而高效的向量相似度搜索库,适用于大规模的向量数据集和高维度的向量数据。它提供了高速的近似搜索和优化的索引结构,有助于构建复杂的检索系统和应用。然而,在使用 Faiss 时需要注意内存消耗和学习曲线的挑战。
安装方法
安装OpenBLAS
OpenBLAS 是一个开源的数值线性代数库,用于高性能科学计算和数据处理。它提供了基于多核处理器和向量指令集的并行化实现,以加速矩阵运算和其他数值计算操作。
git clone https://github.com/xianyi/OpenBLAS.git
gfortran 是 GNU Compiler Collection(简称 GCC)的一部分,它是 GNU 项目开发的免费开源的编译器套件。gfortran 是 GCC 提供的 Fortran 编译器,用于编译和执行 Fortran 程序。
使用gfortran进行编译:
sudo apt install gfortran
cd OpenBLAS
make FC=gfortran
make install
ln -s /opt/OpenBLAS/lib/libopenblas.so /usr/lib/libopenblas.so
LD_LIBRARY_PATH=/opt/OpenBLAS/lib
export LD_LIBRARY_PATH
在这个特定的命令中,FC=gfortran将设置FC变量的值为"gfortran",指示构建过程使用gfortran作为Fortran编译器。
安装lapack
LAPACK(Linear Algebra Package)是一个用于数值线性代数计算的库,它提供了一系列高性能的算法和子程序,用于解决线性方程组、特征值问题、奇异值分解和相关的数值计算任务。
wget http://www.netlib.org/lapack/lapack-3.4.2.tgz
tar -zxf lapack-3.4.2.tgz
cd lapack-3.4.2
cp ./INSTALL/make.inc.gfortran ./
mv make.inc.gfortran make.inc
vi Makefile # 修改如下
[#lib: lapacklib tmglib
lib: blaslib variants lapacklig tmglib]
make
cd lapacke
make
cp include/*.h /usr/include
cd ..
cp *.a /usr/lib
编译Faiss
git clone https://github.com/facebookresearch/faiss.git
cd faiss
#这个命令是使用 CMake 构建一个项目,并将构建产物放置在名为 “build” 的目录中。
cmake -B build . -DFAISS_ENABLE_GPU=OFF -DFAISS_ENABLE_PYTHON=OFF
#这个命令是使用 make 构建名为 “faiss” 的目标,并且指定构建目录为 “build”。
make -C build -j faiss
#这个命令是使用 make 进行构建,并将构建产物安装到系统中。同样在build目录下构建
make -C build install
代码示例
余弦相似度计算
给定一个向量,在已有的两个向量中,找到余弦相似度最优的一个向量:
#include <iostream>
#include <cmath>
#include <faiss/IndexFlat.h>
#include <faiss/index_io.h>
#include <faiss/utils/distances.h>
int main() {// 创建索引对象faiss::IndexFlatIP index(2); // 使用L2距离度量,2维向量// 添加向量数据float xb[4] = {1.0, 1.0, 0.0, 0.5}; // 2个2维向量//存储向量个数:int n=2;// 为了使用内积求出余弦相似度,要对每个向量进行归一化操作size_t d = 2; // 向量维度float norm[d]={0,0};// 计算向量的 L2 范数,是已经过开方的// 函数有四个参数:// x:指向输入向量数组的指针,所有向量在内存中是连续存储的。即向量数组的布局是 [x₀₀, x₀₁, ..., xₙ₋₁(d-1)]。// norms:指向输出结果数组的指针,用于存储计算出的 L2 范数。结果数组的布局和输入向量相同,即 [norm₀, norm₁, ..., normₙ₋₁]。// d:向量的维度,即每个向量的元素数目。// n:向量的数量(或者说是向量数组的长度)。faiss::fvec_norms_L2(norm, xb,d,n); // 将每个向量归一化为单位向量,同时添加到索引中#pragma omp parallel{#pragma omp forfor (int i = 0; i < n; i++) {// 每个向量的起始地址float* vector = &xb[i * d]; // 将向量归一化为单位向量for (size_t j = 0; j < d; j++) {vector[j] /= norm[i];}// 每次将1个向量添加到索引中#pragma omp critical{index.add(1, vector);}}//进行同步#pragma omp barrier}// 保存索引到文件faiss::write_index(&index, "index.faissindex");// 从文件加载索引faiss::Index* loaded_index = faiss::read_index("index.faissindex");// 执行搜索float xq[2] = {1.0, 0.0}; // 查询向量int k = 1; // 返回最接近的2个邻居faiss::idx_t* I = new faiss::idx_t[k]; // 邻居索引float* D = new float[k]; // 邻居距离// search 方法的主要参数如下:
// n:表示要搜索的查询向量的数量,即查询向量的个数。
// x:一个指向浮点数的指针,表示查询向量的数据。x 的大小应该为 n 乘以向量的维度。
// k:表示要返回的相似邻居的数量。
// distances:一个指向浮点数的指针,用于存储查询向量与相似邻居之间的距离。distances 的大小应该为 n 乘以 k。
// labels:一个指向整数的指针,用于存储相似邻居的索引(标签)。labels 的大小应该为 n 乘以 k。loaded_index->search(1, xq, k, D, I);// 打印结果std::cout << "查询结果:" << std::endl;std::cout << "邻居索引: " << I[0] << ", 距离: " << D[0] << std::endl;//返回原始向量:// 获取索引为 i 的向量// 向量的维度std::vector<float> vectors(index.d);index.reconstruct(I[0], vectors.data());// 使用循环遍历并打印该向量每个元素for (const auto& element : vectors) {std::cout << element << " ";}std::cout << std::endl;// 释放内存delete loaded_index;delete[] I;delete[] D;return 0;
}
对应cmakelist:
cmake_minimum_required(VERSION 3.5)
project(fangdou)
FIND_PACKAGE( OpenMP REQUIRED)
if(OPENMP_FOUND)
message("OPENMP FOUND")
set(CMAKE_C_FLAGS "${CMAKE_C_FLAGS} ${OpenMP_C_FLAGS}")
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} ${OpenMP_CXX_FLAGS}")
set(CMAKE_EXE_LINKER_FLAGS "${CMAKE_EXE_LINKER_FLAGS} ${OpenMP_EXE_LINKER_FLAGS}")
endif()# 添加 Faiss 库的路径
set(FAISS_INCLUDE_DIR /usr/local/include/faiss)
set(FAISS_LIBRARY_DIR /usr/local/lib)include_directories(
${FAISS_INCLUDE_DIR}
)SET(OpenCV_DIR /usr/local/lib/cmake/opencv4/)
FIND_PACKAGE(OpenCV REQUIRED)file(GLOB_RECURSE cpp_srcs ${CMAKE_SOURCE_DIR}/src/*.cpp ${CMAKE_SOURCE_DIR}/src/*.cc ${CMAKE_SOURCE_DIR}/src/*.h)link_directories(
/usr/lib/x86_64-linux-gnu/
${FAISS_LIBRARY_DIR}
)add_executable(${PROJECT_NAME} ${cpp_srcs})target_link_libraries(${PROJECT_NAME} ${OpenCV_LIBS} faiss openblas)
输出ID号而非索引的改进版
#include <iostream>
#include <cmath>
#include <faiss/IndexFlat.h>
#include <faiss/index_io.h>
#include <faiss/utils/distances.h>
#include <faiss/IndexIDMap.h>
int main() {// 创建一个IndexFlatIP内积索引对象作为内部索引faiss::IndexFlatIP inner_index(2);// 创建一个IndexIDMap对象,将内部索引设置为IndexFlatIPfaiss::IndexIDMap index(&inner_index);// 添加向量数据float xb[4] = {1.0, 1.0, 0.0, 0.5}; // 2个2维向量//idsfaiss::idx_t ids[] = {1001, 1002};//存储向量个数:int n=2;// 为了使用内积求出余弦相似度,要对每个向量进行归一化操作size_t d = 2; // 向量维度float norm[d]={0,0};// 计算向量的 L2 范数,是已经过开方的// 函数有四个参数:// x:指向输入向量数组的指针,所有向量在内存中是连续存储的。即向量数组的布局是 [x₀₀, x₀₁, ..., xₙ₋₁(d-1)]。// norms:指向输出结果数组的指针,用于存储计算出的 L2 范数。结果数组的布局和输入向量相同,即 [norm₀, norm₁, ..., normₙ₋₁]。// d:向量的维度,即每个向量的元素数目。// n:向量的数量(或者说是向量数组的长度)。faiss::fvec_norms_L2(norm, xb,d,n); // 将每个向量归一化为单位向量,同时添加到索引中#pragma omp parallel{#pragma omp forfor (int i = 0; i < n; i++) {// 每个向量的起始地址float* vector = &xb[i * d]; // 将向量归一化为单位向量for (size_t j = 0; j < d; j++) {vector[j] /= norm[i];}// 每次将1个向量添加到索引中#pragma omp critical{index.add_with_ids(1, vector,&ids[i]);}}//进行同步#pragma omp barrier}// 保存索引到文件faiss::write_index(&index, "index.faissindex");// 从文件加载索引faiss::Index* loaded_index = faiss::read_index("index.faissindex");// 执行搜索float xq[2] = {1.0, 0.0}; // 查询向量int k = 1; // 返回最接近的2个邻居faiss::idx_t* I = new faiss::idx_t[k]; // 邻居索引float* D = new float[k]; // 邻居距离// search 方法的主要参数如下:
// n:表示要搜索的查询向量的数量,即查询向量的个数。
// x:一个指向浮点数的指针,表示查询向量的数据。x 的大小应该为 n 乘以向量的维度。
// k:表示要返回的相似邻居的数量。
// distances:一个指向浮点数的指针,用于存储查询向量与相似邻居之间的距离。distances 的大小应该为 n 乘以 k。
// labels:一个指向整数的指针,用于存储相似邻居的索引(标签)。labels 的大小应该为 n 乘以 k。loaded_index->search(1, xq, k, D, I);// 打印结果std::cout << "查询结果:" << std::endl;std::cout << "邻居索引: " << I[0] << ", 距离: " << D[0] << std::endl;//此时不再支持返回原向量。// 释放内存delete loaded_index;delete[] I;delete[] D;return 0;
}相关文章:
)
【向量数据库】相似向量检索Faiss数据库的安装及余弦相似度计算(C++)
目录 简介安装方法安装OpenBLAS安装lapack编译Faiss 代码示例余弦相似度计算输出ID号而非索引的改进版 简介 Faiss 是一个强大的向量相似度搜索库,具有以下优点: 高效的搜索性能:Faiss 在处理大规模向量数据时表现出色。它利用了高度优化的索…...
教育培训小程序的设计与功能解析
随着互联网的发展,线上教育逐渐成为一种趋势,越来越多的人开始选择在线学习。而搭建一个适合自己的线上教育小程序,可以为教育机构或个人提供更好的教学和学习体验。在本文中,我们将介绍如何通过一个第三方制作平台来搭建在线教育…...
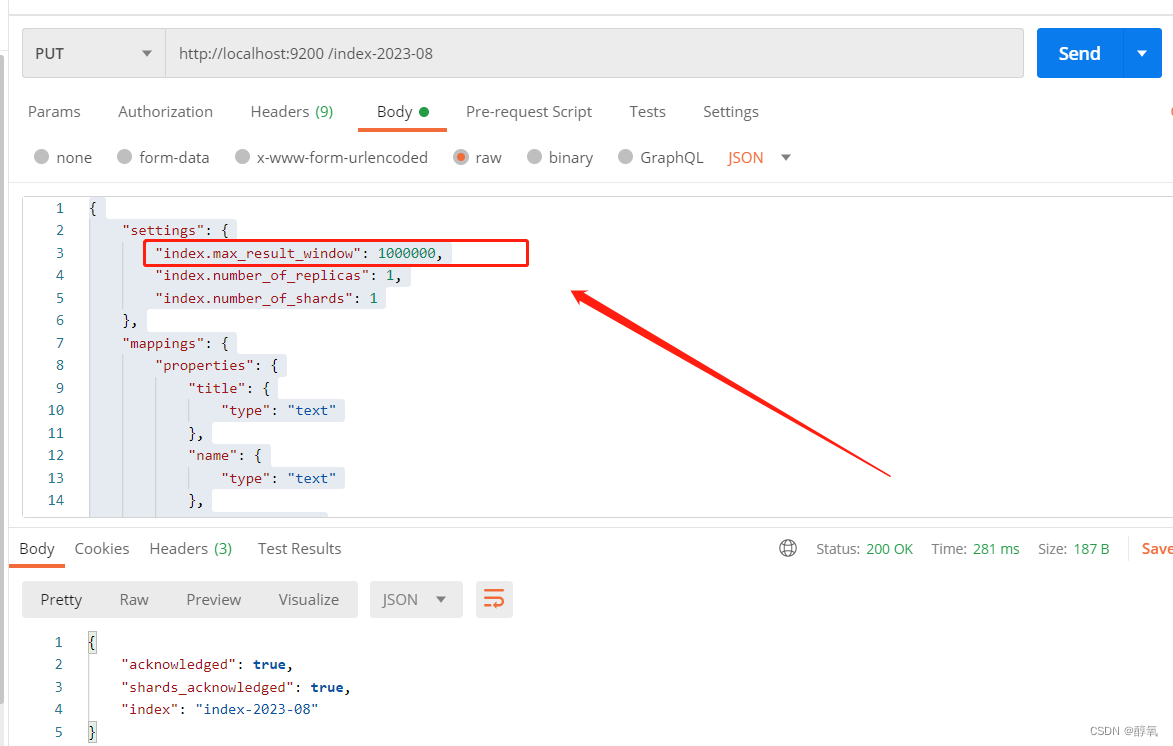
【ES】illegal_argument_exception“,“reason“:“Result window is too large
查询ES数据返回错误: {"root_cause":[{"type":"illegal_argument_exception","reason":"Result window is too large, from size must be less than or equal to: [10000] but was [999999]. See the scroll api for…...

SpringBoot实现登录拦截
如果我们不进行登录拦截的话,即使我们跳过登录页面直接去访问任意一个页面也能访问成功,那么登录功能就没有意义,同时也会存在安全问题,因为有些操作是要用户登录后才能执行的,如果用户没有登录,该接口就获…...

浅谈泛在电力物联网、能源互联网与虚拟电厂
导读:从能源互联网推进受阻,到泛在电力物联网名噪一时,到虚拟电厂再次走向火爆,能源领域亟需更进一步的数智化发展。如今,随着新型电力系统建设推进,虚拟电厂有望迎来快速发展。除了国网和南网公司下属的电…...

深度学习框架安装与配置指南:PyTorch和TensorFlow详细教程
如何安装和配置深度学习框架PyTorch和TensorFlow 为什么选择PyTorch和TensorFlow?PyTorchTensorFlow安装PyTorch 步骤1:安装Python步骤2:使用pip安装PyTorch 安装TensorFlow 步骤1:安装Python步骤2:使用pip安装TensorF…...

vue中属性执行顺序
vue中属性的执行顺序 在Vue 2中,组件的生命周期和数据绑定的执行顺序如下: data:首先,组件会调用 data 函数,该函数返回一个对象,该对象的属性和方法会被分配给组件的 $data。init:接下来&…...

【代码随想录】Day 50 动态规划11 (买卖股票Ⅲ、Ⅳ)
买卖股票Ⅲ https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/ 无语了。。。 写的很好就是怎么都过不了。。。 还是就用代码随想录的写法吧。。。 class Solution { public:int maxProfit(vector<int>& prices) {int n prices.size();vector&…...

PHP反序列化漏洞
一、序列化,反序列化 序列化:将php对象压缩并按照一定格式转换成字符串过程反序列化:从字符串转换回php对象的过程目的:为了方便php对象的传输和存储 seriallize() 传入参数为php对象,序列化成字符串 unseriali…...
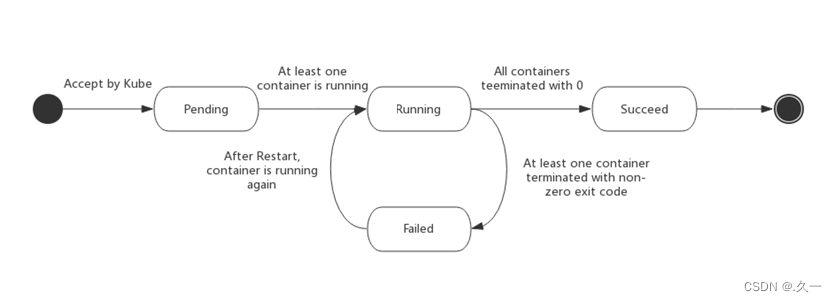
容器编排学习(一)k8s集群管理
一 Kubernetes 1 概述 就在Docker容器技术被炒得热火朝天之时,大家发现,如果想要将Docker应用于具体的业务实现,是存在困难的一一编排、管理和调度等各个方面,都不容易。于是,人们迫切需要一套管理系统࿰…...

js去除字符串空格的几种方式
方法1:(最常用)全部去除掉空格 var str abc d e f g ; function trim(str) { var reg /[\t\r\f\n\s]*/g; if (typeof str string) { var trimStr str.replace(reg,); } console.lo…...

Spring 自带工具——URI 工具UriComponentsBuilder
UriComponentsBuilder 是 Spring Framework 提供的一个实用工具类,用于构建 URI(Uniform Resource Identifier)。URI 是用于标识和定位资源的字符串,例如 URL(Uniform Resource Locator)就是一种特殊的 URI…...
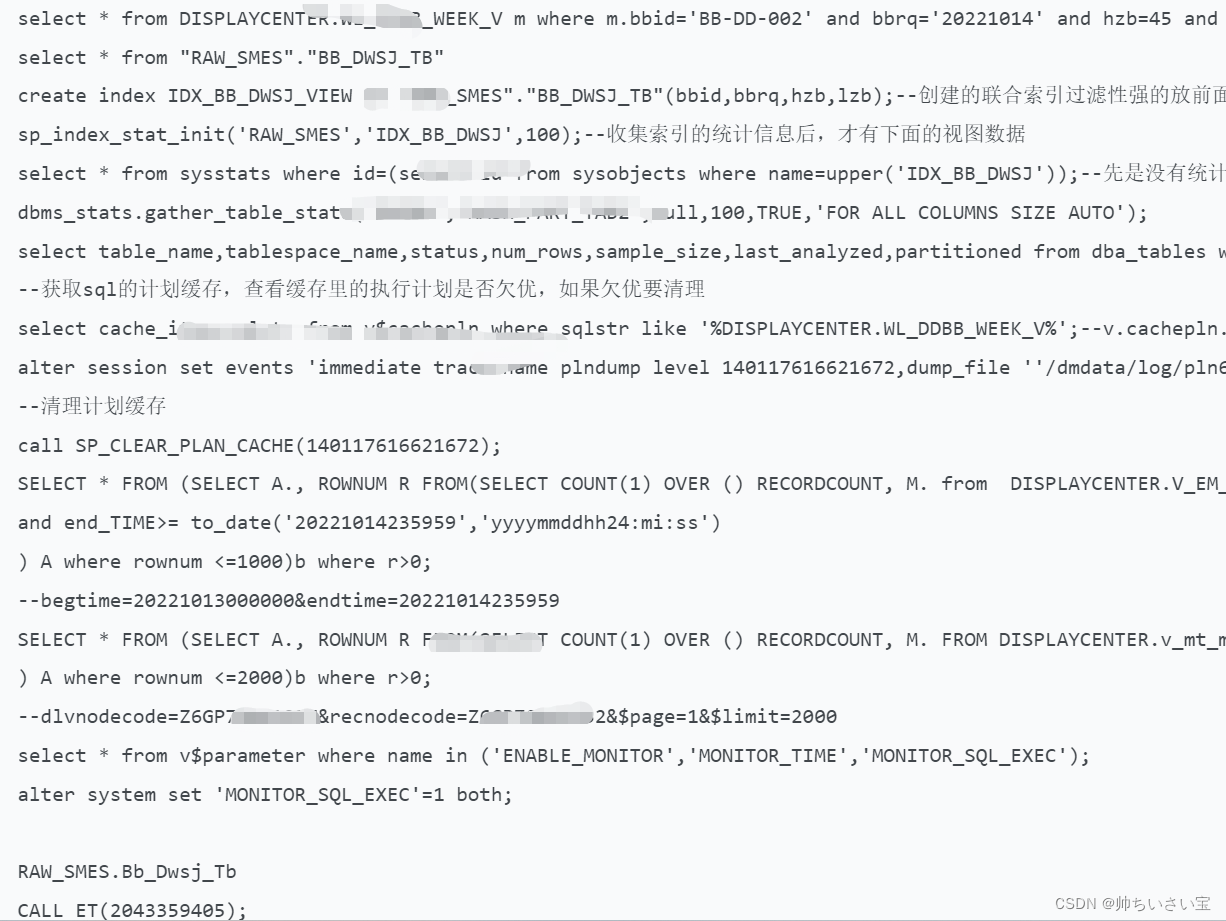
优化案例5:视图目标列改写优化
优化案例5:视图目标列改写优化 1. 问题描述2. 分析过程2.1 目标SQL2.2 解决思路1)效率低的执行计划2)视图过滤性3)查看已有索引定义 2.3 视图改写2.4 增添复合索引 3. 优化总结 DM技术交流QQ群:940124259 1. 问题描述…...
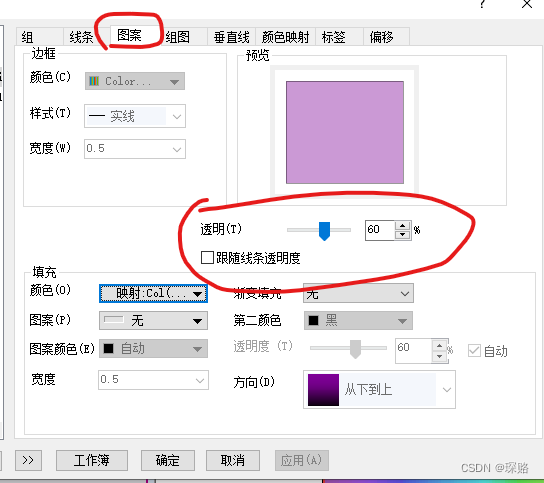
Origin绘制彩色光谱图
成果图 1、双击线条打开如下窗口 2、选择“图案”-》颜色-》按点-》映射-》Wavelength 3、选择颜色映射 4、单击填充-》选择加载调色板-》Rainbow-》确定 5、单击级别,设置成从370到780,右侧增量选择2(越小,颜色渐变越细腻&am…...

项目复盘:从实践中学习
引言 在我们的工作生涯中,每一个项目都是一次学习的机会。项目复盘是对已完成项目的全面评估,旨在理解我们做得好的地方,以及需要改进的地方。这篇文章将分享我们如何进行项目复盘,以及我们从中学到了什么。 项目背景 在我们开…...
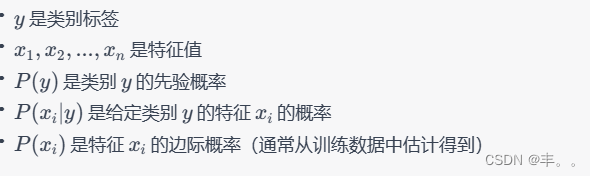
机器学习和数据挖掘02-Gaussian Naive Bayes
概念 贝叶斯定理: 贝叶斯定理是概率中的基本定理,描述了如何根据更多证据或信息更新假设的概率。在分类的上下文中,它用于计算给定特征集的类别的后验概率。 特征独立性假设: 高斯朴素贝叶斯中的“朴素”假设是,给定…...

【面试题精讲】Java Stream排序的实现方式
首发博客地址 系列文章地址 如何使用Java Stream进行排序 在Java中,使用Stream进行排序可以通过sorted()方法来实现。sorted()方法用于对Stream中的元素进行排序操作。具体实现如下: 对基本类型元素的排序: 使用sorted()方法对Stream进行排序…...
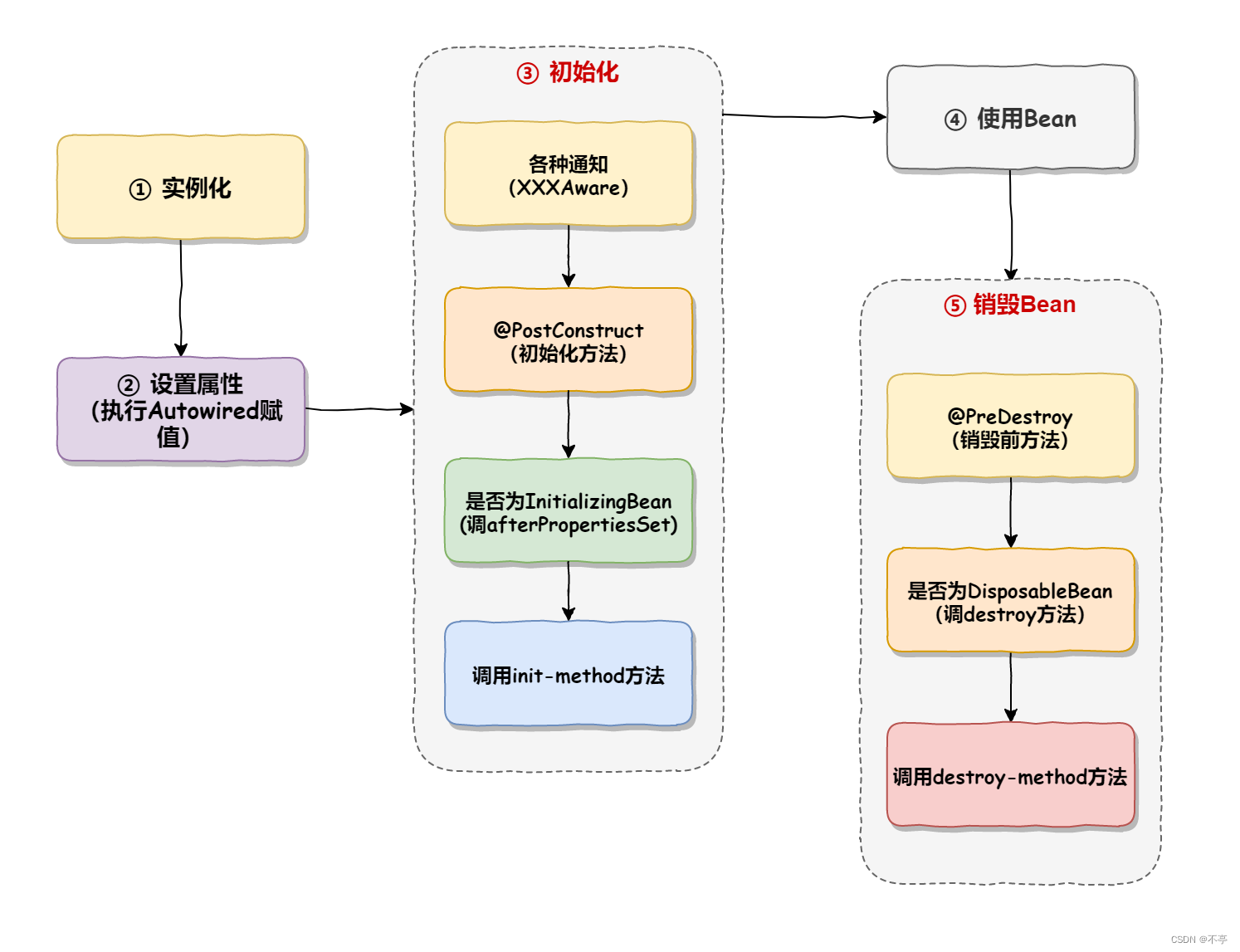
浅谈Spring
Spring是一个轻量级的控制反转(IoC)和面向切面(AOP)的容器(框架)。 一、什么是IOC? IoC Inversion of Control 翻译成中⽂是“控制反转”的意思,也就是说 Spring 是⼀个“控制反转”的容器。 1.1控制反转推导 这个控制反转怎…...
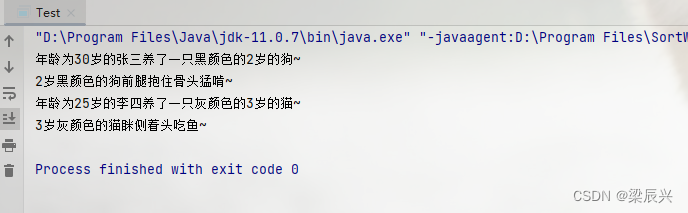
Java 复习笔记 - 面向对象进阶篇
文章目录 一,Static(一)Static的概述(二)静态变量(三)静态方法(四)工具类(五)static的注意事项 二,继承(一)继…...
微信小程序中识别html标签的方法
rich-text组件 在微信小程序中有一个组件rich-text可以识别文本节点或是元素节点 具体入下: //需要识别的数据放在data中,然后放在nodes属性中即可 <rich-text nodes"{{data}}"></rich-text>详情可以参考官方文档:https://developers.weixin.qq.com/mi…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
