Gurobi使用(一)——操作指南(转自知乎)
好像还是要学一下Gurobi如何使用的,不然这代码着实有点抽象了
一、入门操作
一般来说,求解一个数学规划模型的时候,通常会按照如下步骤解决问题:
设置变量---addVar()。
更新变量空间---update()。
设定目标函数---setObjective()。
设定约束条件---addConstr()。
执行最优化---optimize()。
创建模型:
import gurobipy
model = gurobipy.Model('LP模型测试1') # 创建一个模型
(1) 设置决策变量
一次创建一个变量:
x = model.addVar(lb=0.0, ub=gurobipy.GRB.INFINITY, vtype=gurobipy.GRB.CONTINUOUS, name="")- lb=0.0:变量的下界,默认为0.0。
- ub=gurobipy.GRB.INFINITY:变量的上界,默认为无穷大。
- vtype=gurobipy.GRB.CONTINUOUS:变量的类型,默认为连续型号。变为GRB.BINARY则是0-1变量,变为GRB.INTEGER则为整数变量。
- name="":变量名,默认为空。
一次创建多个变量:
x = model.addVars(*indexes, lb=0, ub=gurobipy.GRB.INFINITY, vtype=gurobipy.GRB.CONTINUOUS, name="")示例:
x = model.addVars(3, 4, 5, vtype=gurobipy.GRB.BINARY, name="C")一次性生成3x4x5个变量。x包含了3x4x5个变量,可以通过x[i,j,k]来访问单个的变量。
(2)更新变量空间
model.update()(3)设定目标函数
单目标优化
model.setObjective(expression,sense=None)- expression:表达式,可以是一次或者二次函数的类型。
- sense:求解类型,GRB.MINIMIZE则为最小值,GRB.MAXMIZE则为最大值。
model.setObjective(8 * x1 + 10 * x2 + 7 * x3 + 6 * x4 + 11 * x5 + 9 * x6, gurobipy.GRB.MINIMIZE)多目标优化代码:
model.setObjectiveN(expression, index, priority=0, weight=1.0, abstol=0, reltol=0, name="")- expression:表达式,可以是一次或者二次函数类型。
- index:目标函数对应的序号(默认0,1,2,...),以index=0作为目标函数的值,其余值需要另外设置参数。
- priority:分层序列法多目标决策的优先级,值越大优先级越高。
- weight:线性加权多目标决策权重(在优先级相同的时候发挥作用)。
- abstol:分层序列法多目标决策时允许的目标函数值的最大降低量。
- reltol:分层序列法多目标决策时允许的目标函数值的最大降低比率。
(4)添加约束条件:
创建一个约束条件
model.addConstr(expression, name="")- expression: 布尔表达式,可以是一次或二次函数类型
- name: 约束式的名称
model.addConstr(12 * x1 + 9 * x2 + 25 * x3 + 20 * x4 + 17 * x5 + 13 * x6 >= 60, "c0")创建多个约束条件
model.addConstrs(expressions, name="")创建一个指示变量约束
model.addGenConstrIndicator(binvar, binval, expression, name="")指示变量 binvar 的值取 binval 时, 进行约束 expression
或者
方法1: 构造指示变量 ,则上述约束转化为: (M是一个很大的数,可以取1000)
方法2:转化为二次约束,但是如果矩阵为非正定矩阵,则无法求解:
(5)执行最优化
model.Params.LogToConsole=True # 显示求解过程
model.Params.MIPGap=0.0001 # 百分比界差
model.Params.TimeLimit=100 # 限制求解时间为 100s
model.Params.Presolve = -1 # 预处理程度, 0关闭,1保守,2激进
model.Params.MIPFocus = 0 # 求解侧重点. 1快速找到可行解, 2证明最有, 3侧重边界提升, 0均衡搜索
model.Params.SolutionLimit = inf # 求解数量, 默认求所有解, 比较出最优的结果, 只需要可行解时可以设置该参数为1
model.Params.NonConvex = 1 # 默认求解器,改为 2 时可以解决非凸二次优化问题
model.optimize()(6)查看模型优化结果
- 查看函数值以及变量值
# 查看单目标规划模型的目标函数值
print("Optimal Objective Value", model.objVal)
# 查看多目标规划模型的目标函数值
for i in range(model.NumObj):MODEL.setParam(gurobipy.GRB.Param.ObjNumber, i)print(f"Obj {i+1} = {model.ObjNVal}")
# 查看变量取值
for var in model.getVars():print(f"{var.varName}: {round(var.X, 3)}")(7)辅助函数
quicksum()
quicksum相当于sum及其求和符号,效率更高。
写为:
for i in I:model.addConstr(quicksum(x[i,j] for j in J) <= 5)此外,它还支持迭代器、生成器协议,也就是说,可以通过下面的代码,实现更为复杂的过滤、求和方法.
for c in C:model.addConstr(gurobipy.quicksum(x[d,i,j] for d in D for i in range(0, 24) for j in range(i + 1, 25) if i <= c < j) >= R[c])
相关文章:
——操作指南(转自知乎))
Gurobi使用(一)——操作指南(转自知乎)
好像还是要学一下Gurobi如何使用的,不然这代码着实有点抽象了 一、入门操作 一般来说,求解一个数学规划模型的时候,通常会按照如下步骤解决问题: 设置变量---addVar()。 更新变量空间---update()。 设定目标函数---setObjective()。 设定约…...
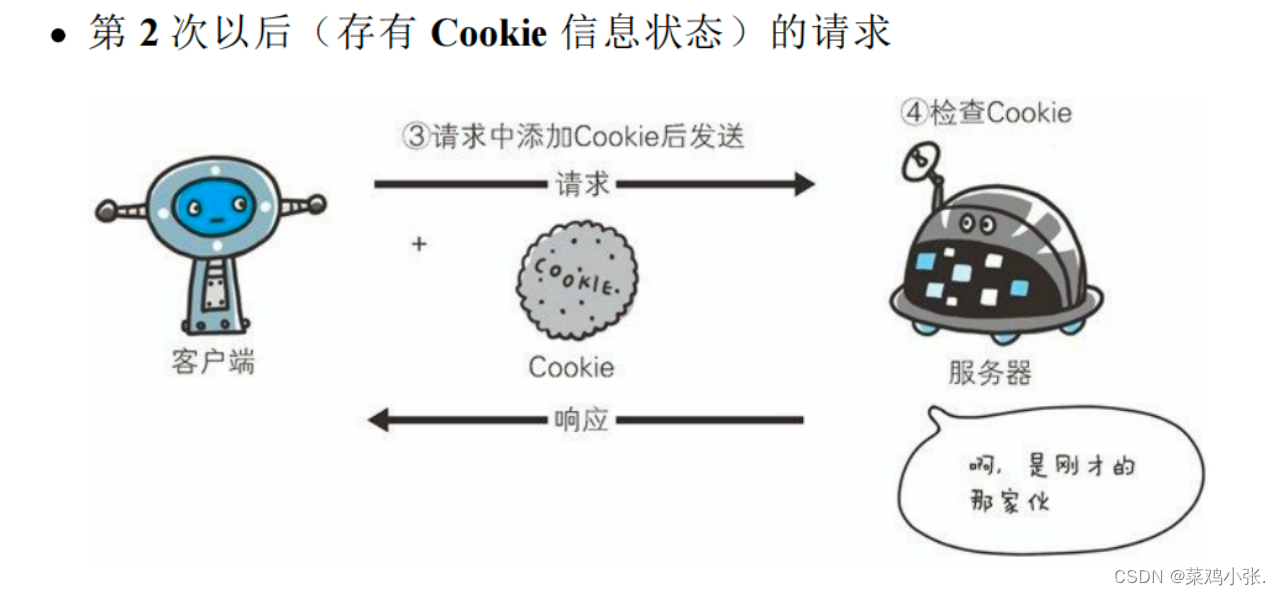
计算机网络的故事——简单的HTTP协议
简单的HTTP协议 文章目录 简单的HTTP协议一、简单的HTTP协议 一、简单的HTTP协议 HTTP是不保存状态的协议,为了实现保存状态功能于是引入了Cookie技术。 method: get:获取资源 post:传输实体主体 put:传输文件 head:获取报文首部,用于确认URI的有效性以…...
新能源商用车软件开发设计规范
目 录 前 言.............................................................................................................. 1 1 范围............................................................................................................... 2 2 规范性…...
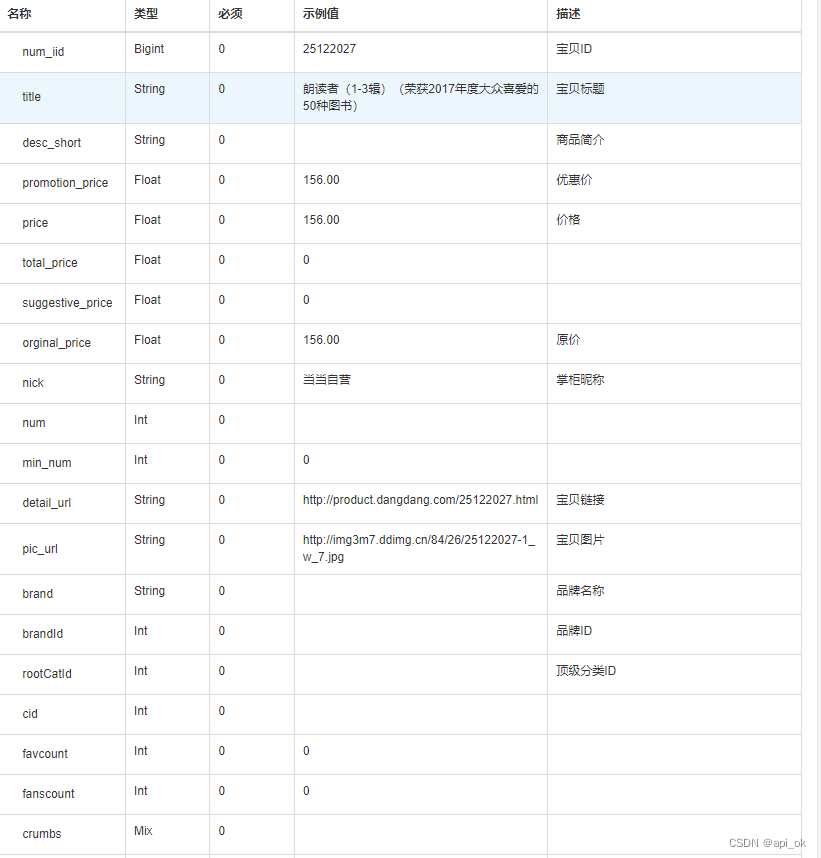
Json“牵手”当当网商品详情数据方法,当当商品详情API接口,当当API申请指南
当当网是知名的综合性网上购物商城,由国内著名出版机构科文公司、美国老虎基金、美国IDG集团、卢森堡剑桥集团、亚洲创业投资基金(原名软银中国创业基金)共同投资成立1。 当当网从1999年11月正式开通,已从早期的网上卖书拓展到网…...

lazarus开发界面程序用线程显示进度条
lazarus开发界面程序用线程显示进度条,效果更好,以前没有另外显示线程,遇到上传文件或其他较长时间操作,界面就卡在那里,体验不好,现在另外启动线程操作,主界面就不至于卡在那里。 首先在主界面…...
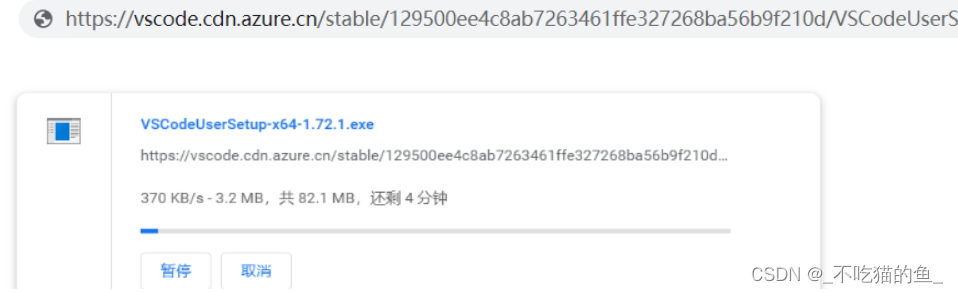
解决VSCode下载速度特别慢的问题
一、下载VSCode 1.打开VSCode官网 https://code.visualstudio.com 2.download下载 3.下载特别慢 二、解决VSCode下载速度特别慢 1.单击右下角全部显示 我是用chrome浏览器,点击右下角的全部显示按钮,可以跳转到下载内容页面。 如果你是用其他浏览器…...
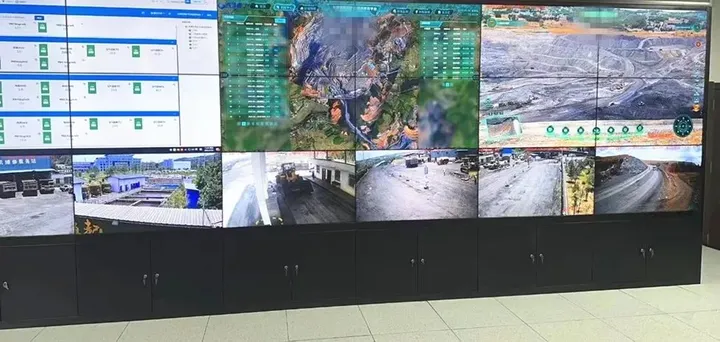
国家矿山安全监察局关于露天矿山边坡监测系统建设及预警响应要求
矿山是人类社会发展的物资基础,也是国民经济的重要组成部分。随着我国经济的快速增长,矿山开发步伐加快,使得边坡问题日益严重,影响了矿山的安全生产。为有效防范遏制矿山重特大事故发生,国家矿山安全监察局在8月30日发…...
前端使用elementui开发后台管理系统的常用功能(持续更新)
前言:本次的文章完全是自己开发中遇到的一些问题,经过不断的修改终于完成的一些功能,当个快捷的查看手册吧~ elementui开发后台管理系统常用功能 高级筛选的封装elementui的表格elementui的表格实现跨页多选回显elementui的表单elementui的日…...
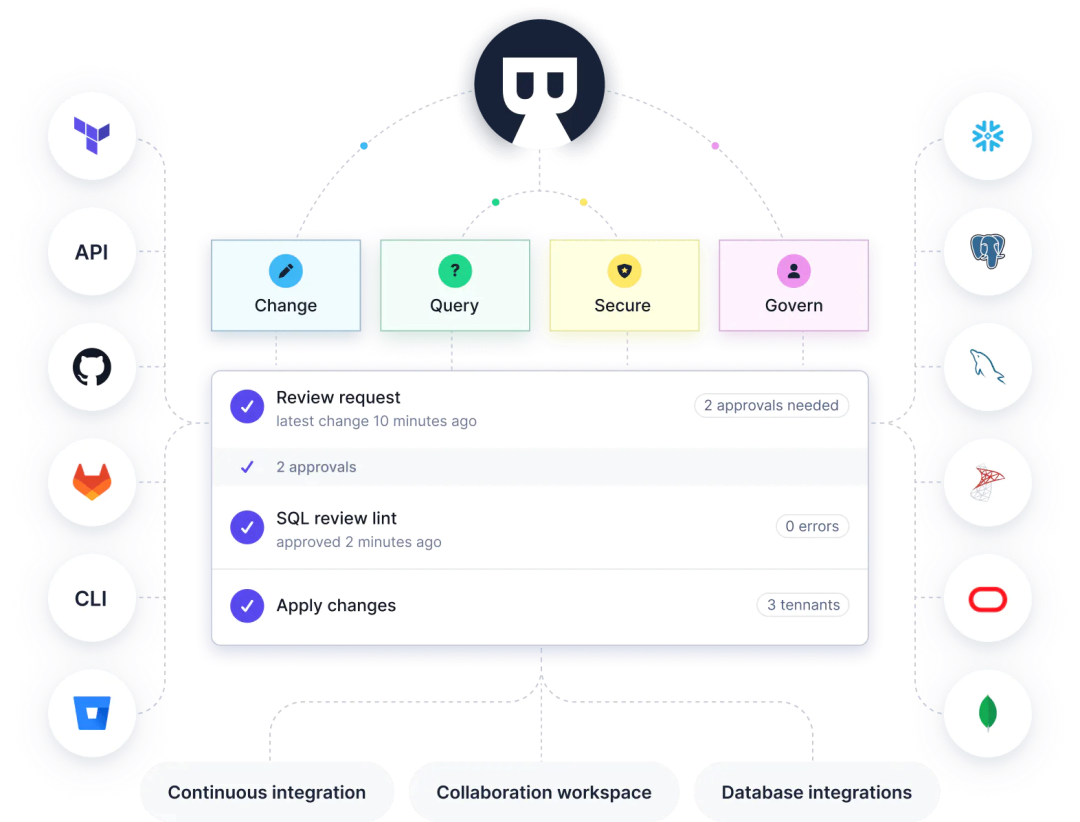
中东 Shopify 如何使用 Bytebase 构建一站式数据库开发工作流
公司简介 Salla 是一家 2016 年成立,位于沙特麦加的自建站电商平台。 作为中东 Shopify,其最大的特点是支持阿拉伯语建站,并且提供更多适应中东地区特点的本地化服务。截止目前,已有 47,000 家店铺入驻 Salla,商品销售…...

谷歌Chrome庆祝15周年,推出全新设计!了解最新信息!
谷歌浏览器本月将满15岁,为了纪念这一时刻,它正在进行改造和升级。 这一点意义重大,因为Chrome在全球有数十亿人使用,因此谷歌所做的每一项改变都会对互联网以及这些人与互联网的互动方式产生巨大影响。即使你不使用Chrome或不关…...
)
解决Oracle SQL语句性能问题——SQL语句改写(分析函数、with as、union及or)
1. 正确使用分析函数 分析函数最早出现于Oracle 8i版本中,并在后续版本中不断得以增强。正确的使用分析函数,不但能非常方便的实现某些功能,而且,在某些场景中,还可以大幅提升SQL语句的性能。因此,为了简化应用实现逻辑或解决相关SQL语句性能问题,有时我们需要利用分析…...
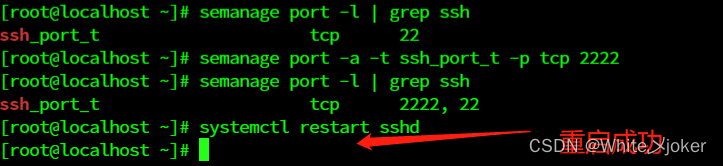
Linux之SELinux
目录 概述 定义 作用 SELinux与传统的权限区别 SELinux工作原理 名词解释 主体(Subject) 目标(Object) 策略(Policy) 安全上下文(Security Context) 文件安全上下文查看 …...

Acwing算法心得——街灯(差分)
大家好,我是晴天学长,差分广泛用于一段范围的加减运算,可以优化时间复杂度,需要的小伙伴请自取哦!如果觉得写的不错的话,可以点个关注哦,后续会继续更新的。💪💪…...
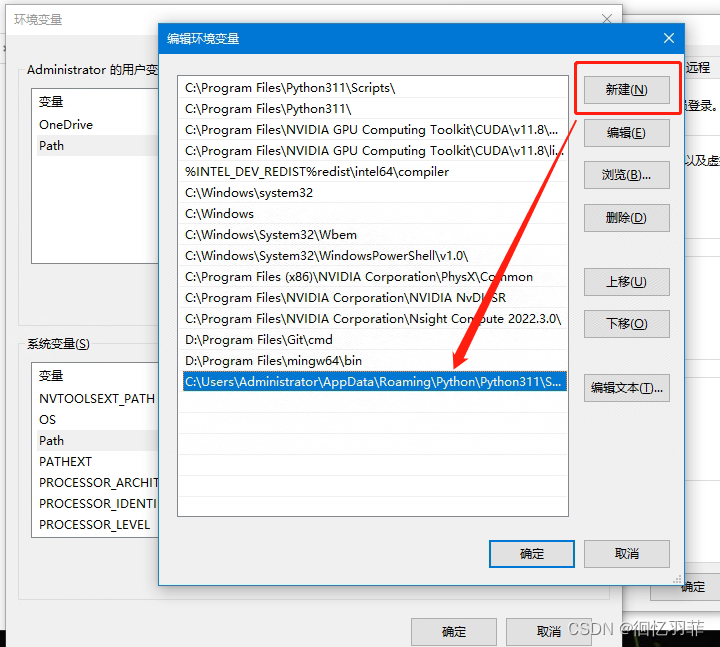
streamlit执行报错WARNING,重新安装碰到问题如何解决
streamlit执行报错WARNING,重新安装碰到问题如何解决 如何解决1、卸载已经安装的程序2、再次安装程序3、出现如下yinstaller 警告问题:4、又出现“which is not on PATH”警告。5、解决方案 发现在安装的时候有很多WARNING出现,但是没有但回事…...

《C++设计模式》——行为型
前言 行为型模式是对在不同的对象之间划分责任和算法的抽象化。行为型模式不仅仅关注类和对象的结构,而且重点关注它们之间的相互作用。 Interpreter(解释器) Template Method(模板方法) GOOD:把不变的代码部分都转移到父类中,将可变的代…...

什么是原生IP?原生IP与住宅IP有何区别?
相信许多做跨境的都会接触到IP代理,比如电商平台、社媒平台、收款平台等等,都会检测IP。那也会经常听到一些词汇:原生IP、住宅IP,这两者之间有什么区别呢?什么业务需要用到呢?接下来带大家具体了解一下。 什…...

element-plus 表格-自定义样式实现
效果如下 代码如下 <template><h2>表格自定义样式</h2><div style"background-color: cadetblue; height: 600px;"><div class"regulaContainer"><el-table ref"tableRef" :data"tableData" border …...

MVCC
MVCC(Multi-Version Concurrency Control)是数据库管理系统(DBMS)中的一种技术,用于管理并发访问数据,允许多个事务同时进行而不互相干扰,同时保持数据的一致性。 MVCC 的工作原理如下…...

你不知道的JavaScript---对象
1.语法 对象可以通过两种方式定义:一种是对象字面量形式,一种是构造形式 对象字面量: var muObject {key: value }构造形式的: var myObject new Object() myObject.key value不管是使用对象字面量形式还是构造形式创建出来…...

C++项目实战——基于多设计模式下的同步异步日志系统-①-项目介绍
文章目录 专栏导读项目介绍开发环境核心技术环境搭建日志系统介绍1.为什么需要日志系统2.日志系统技术实现2.1同步写日志2.2异步写日志 专栏导读 🌸作者简介:花想云 ,在读本科生一枚,C/C领域新星创作者,新星计划导师&a…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
