【C++】模拟实现二叉搜索树的增删查改功能


个人主页:🍝在肯德基吃麻辣烫
我的gitee:C++仓库
个人专栏:C++专栏
文章目录
- 一、二叉搜索树的Insert操作(非递归)
- 分析过程
- 代码求解
- 二、二叉搜索树的Erase操作(非递归)
- 分析过程
- 代码求解
- 三、二叉搜索树的Find操作
- 代码求解
- 四、构造+拷贝构造+析构+赋值重载
- 节点的代码
- 构造函数
- 拷贝构造函数
- 赋值运算符重载
- 析构函数
- 二叉搜索树递归版本
- 插入操作递归版本
- 删除操作递归版本
- 总结
一、二叉搜索树的Insert操作(非递归)
分析过程
假如这里有一棵树,我们需要对这棵树插入一个新的节点:
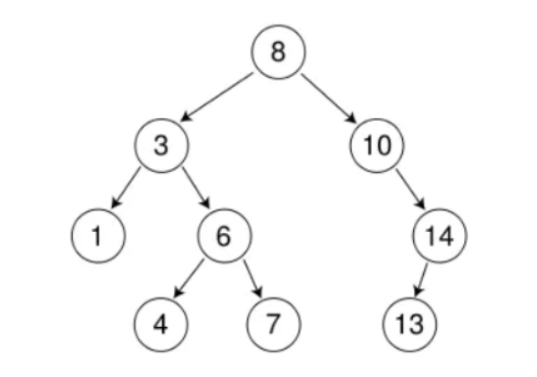
- 假如需要插入16这个节点。
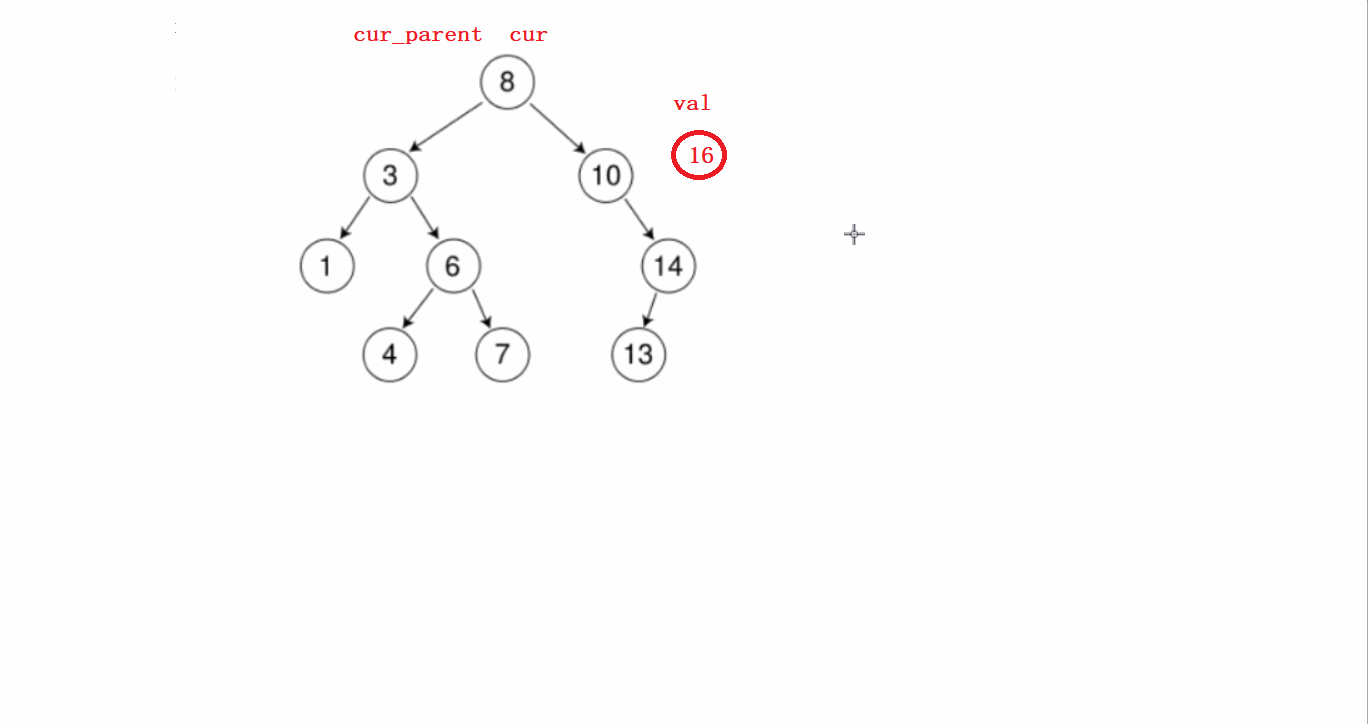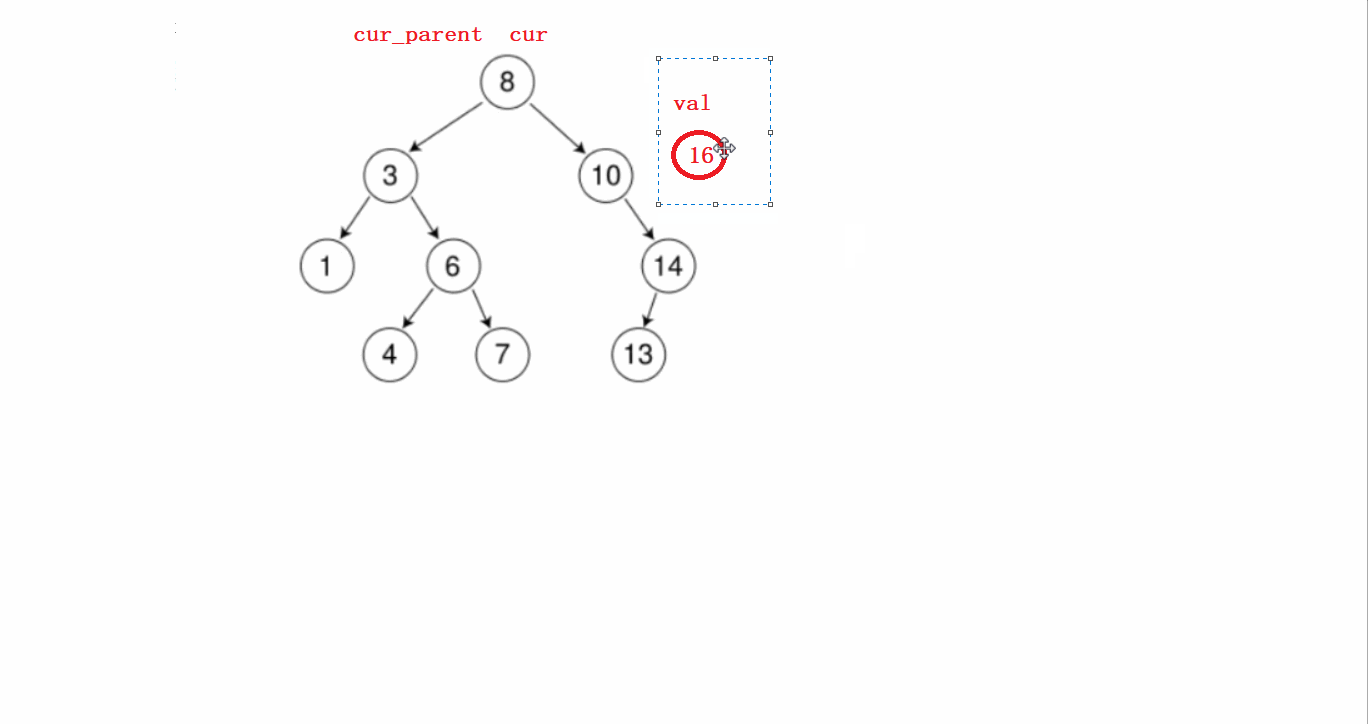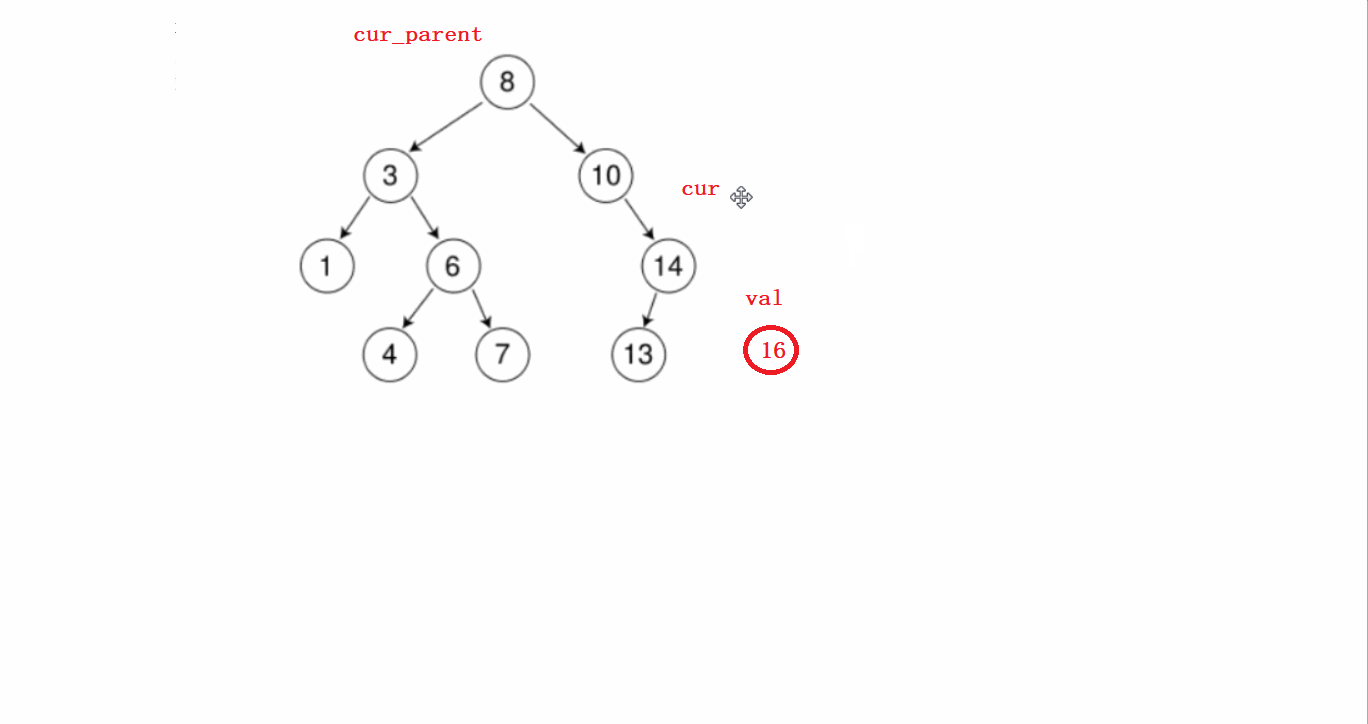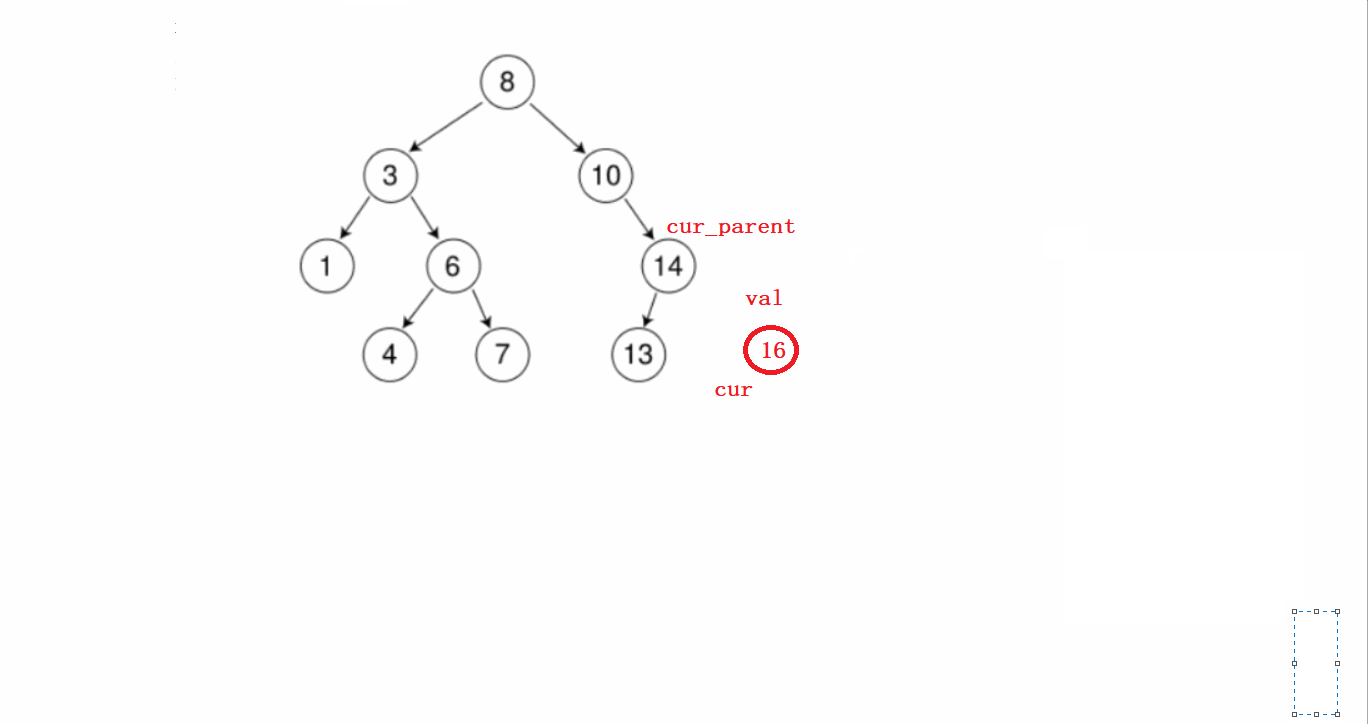
要分几个步骤进行:
1)先从根节点开始判断待插入节点和根节点谁大,根节点大就往左比较,根节点小了就往右比较。
第一步这个过程需要提前记录节点的父亲。
2)找到待插入位置后,先new一个新的节点;然后判断该节点是在前面记录的父亲节点的左边还是右边,然后连接起来即可。
代码求解
bool _Insert(Node* root, const T& val)
{if (root == nullptr){root = new Node(val);return true;}Node* cur = _root;Node* cur_par = _root;//找插入位置while (cur){if (val > cur->_val){cur_par = cur;cur = cur->_right;}else if (val < cur->_val){cur_par = cur;cur = cur->_left;}//相同就不能插入else{cout << "无法插入" << endl;return false;}}//找到插入位置了,记录父亲Node* insNode = new Node(val);if (cur_par->_val < val){cur_par->_right = insNode;return true;}else{cur_par->_left = insNode;return true;}
}
二、二叉搜索树的Erase操作(非递归)
分析过程
以下面这棵树为例:
假如我们要删除7这个节点。
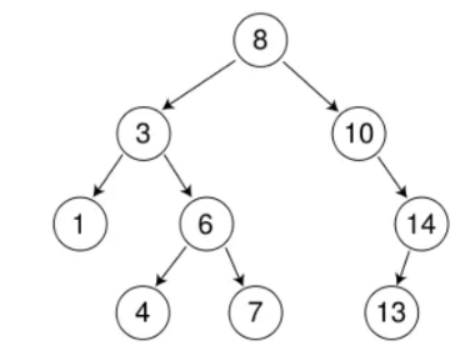
1)查找该节点是否存在于树中。
2)如果存在,先判断该节点属于下面的哪种类型:
- 1)删除的节点是叶子节点,直接删除即可。
- 2)删除的节点只有一个孩子,需要先判断它的孩子是
left还是right,然后让该节点的父亲节点指向它的孩子即可。 - 3)如果删除的节点有
left和right两个孩子,需要找一个节点进行替换;来保证这棵树在删除一个节点后还是一棵二叉搜索树。该找哪个节点来替换呢? -
- 1)找删除节点的左子树的最大节点(最右)
-
- 2)找删除节点的右子树的最小节点(最左)
找这两个节点的任意一个均可。
在这里可能有个疑问,万一找不到呢?
你放心吧!一定能找到,这是二叉搜索树的特性。
找到该节点后,将该节点与待删除的节点进行交换,然后删除交换后的节点即可。
在上面的例子中,很显然7属于叶子节点,直接删除即可。
需要注意的是:
我们在寻找那个替代节点时,像插入一样,需要记录它的父
亲,这样在删除的时候才能知道删除left孩子还是right孩子。
代码求解
bool _Erase(Node* root,const T& val)
{//第一步:先找到要删除的节点Node* cur = root;Node* cur_parent = cur;while (cur){if (cur->_val > val){cur_parent = cur;cur = cur->_left;}else if (cur->_val < val){cur_parent = cur;cur = cur->_right;}//找到了//待删除的节点分三种情况else{//1.左右子树为空;2.其中一个子树为空if (cur->_left == nullptr){//要知道我是父亲的左还是右if (cur_parent->_left == cur){cur_parent->_left = cur->_right;}else if (cur_parent->_right == cur){cur_parent->_right = cur->_right;}}else if (cur->_right == nullptr){//要知道我是父亲的左还是右if (cur_parent->_left == cur){cur_parent->_left = cur->_left;}else if (cur_parent->_right == cur){cur_parent->_right = cur->_left;}}//3.删除的节点左右都不为空else{//先找替代节点//找左子树的最大节点或者右子树的最小节点来替代// 最右 最左Node* lParent = cur;Node* leftMax = cur->_left;while (leftMax->_right){lParent = leftMax;leftMax = leftMax->_right;}//找到了,进行替换swap(cur->_val, leftMax->_val);//替换完成后,必须删除该节点,不能用递归删除。//因为如果用递归,可能就找不到要删除的节点了//这里还要判断leftMax这个替换节点是它父亲的左还是右子节点//因为有一种极端情况是,leftMax是在父亲的左边if (lParent->_right == leftMax){lParent->_right = leftMax->_left;//leftMax是左子树的最右节点了,它不会有右孩子,但可能有左孩子}else if (lParent->_left == leftMax){lParent->_left = leftMax->_left;}cur = leftMax;}delete cur;cur = nullptr;return true;}}return false;
}
三、二叉搜索树的Find操作
查找节点过于简单,直接贴代码。
代码求解
bool _Find(Node* root, const T& val)
{if (root == nullptr){return false;}Node* cur = _root;while (cur){if (cur->_val < val){cur = cur->_right;}else if (cur->_val > val){cur = cur->_left;}else{return true;}}return false;
}
四、构造+拷贝构造+析构+赋值重载
节点的代码
template<class T>
struct BSTreeNode
{BSTreeNode(const T& val):_left(nullptr), _right(nullptr), _val(val){}BSTreeNode<T>* _left;BSTreeNode<T>* _right;T _val;
};
构造函数
BSTree():_root(nullptr)
{}
拷贝构造函数
拷贝构造就是将一棵已有的树对每一个节点进行拷贝即可。
这个过程是深拷贝。
由于我们需要将每一个节点都进行拷贝并连接起来。所以这里需要前序遍历的思想处理。
Node* Copy(Node* root)
{if (root == nullptr){return nullptr;}Node* Copyroot = new Node(root->_val);Copyroot->_left = Copy(root->_left);Copyroot->_right = Copy(root->_right);return Copyroot;
}
赋值运算符重载
这里的赋值重载可以用现代写法:
1)先将原树传给operator=()函数,用生成临时对象的方式传递,然后让被赋值的树的_root与该临时对象树的_root进行交换即可。
BSTree<T>& operator=(BSTree<T> t)
{swap(_root, t._root);return *this;
}
这样写的好处是:
1)t是一个临时对象,出了作用域会自己调用析构函数进行销毁。
2)_root和t._root交换后,原来这棵树会被临时对象销毁。
析构函数
将一棵树的每一个节点进行释放,就需要从下往上进行逐一释放,这个就用到后续遍历的思想。
~BSTree()
{Destroy(_root);
}//后续遍历销毁
void Destroy(Node* root)
{if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;
}
二叉搜索树递归版本
插入操作递归版本
原理与非递归版本是一样的。
最大的区别是,在root的前面加上了一个引用。
- 1)先找到待插入位置
- 2)进行插入即可。
这里不再需要记录父亲的原因是:
加了引用后,当遇到空节点时,让
root = new Node(val);
这个操作即可,因为当前的root是上一层栈帧的root节点的孩子(不用管是左孩子还是右孩子)
执行完成这个代码后,相当于让上一层栈帧中的root的孩子
指向了一个New出来的节点。这样就完成了插入。
bool _InsertR(Node*& root, const T& val)
{if (root == nullptr){root = new Node(val);return true;}if (root->_val < val){_InsertR(root->_right, val);}else if (root->_val > val){_InsertR(root->_left, val);}//相同不能插入return false;
}
删除操作递归版本
删除的过程与非递归版本是一样的。
1)先找到删除的节点。
找到该节点后,该节点同样有三种情况:
- 1)该节点是叶子节点
- 2)该节点只有一个孩子
- 3)该节点有两个孩子(需要找替代节点)
前面两种情况的处理方法是一样的。
2)判断该节点是属于上面三种的哪一种,如果是前面两种,只需要判断该节点的left为空还是right为空即可。
就相应地执行:
root = root->_right;
或者
root = root->_left;
这两个操作即可。
以为当前栈桢的root是上一层栈桢中root的孩子(不用管是做孩子还是右孩子)
这个代码的意思就是:
让上一层栈桢的root的left/right指向当前层栈桢的root的left/right

bool _EraseR(Node*& root, const T& val)
{if (root == nullptr){return false;}if (root->_val < val){return _EraseR(root->_right, val);}else if (root->_val > val) {return _EraseR(root->_left, val);}//找到了else{Node* del = root;//同样有三种情况//这是因为root是上一个root的left/right的别名if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{//找到替代的节点Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}//找到之后,交换swap(leftMax->_val, root->_val);return _EraseR(root->_left, val);//不能这样//return _Erase(leftMax, val);//这样不能保证连接关系正确}delete del;return true;}
}
总结
本文章讲述了二叉搜索树的增删查改功能,其中有一些细节需要特别注意。
相关文章:

【C++】模拟实现二叉搜索树的增删查改功能
个人主页:🍝在肯德基吃麻辣烫 我的gitee:C仓库 个人专栏:C专栏 文章目录 一、二叉搜索树的Insert操作(非递归)分析过程代码求解 二、二叉搜索树的Erase操作(非递归)分析过程代码求解…...

Yolov8-pose关键点检测:模型轻量化创新 | ScConv结合c2f | CVPR2023
💡💡💡本文解决什么问题:ScConv(空间和通道重建卷积),一个即插即用的架构单元,可以可以直接用来替代各种卷积神经网络中的标准卷积。 ScConv | GFLOPs从9.6降低至9,参数量从6482kb降低至6479kb Yolov8-Pose关键点检测专栏介绍:https://blog.csdn.net/m0_637742…...
)
【洛谷 P1060】[NOIP2006 普及组] 开心的金明 题解(动态规划+01背包)
[NOIP2006 普及组] 开心的金明 题目描述 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说…...
)
什么是CI/CD:持续集成与持续交付?(InsCode AI 创作助手)
在现代软件开发领域,CICD(Continuous Integration and Continuous Delivery)是一种关键性的开发实践,它有助于提高软件交付的质量和效率。本文将深入探讨CICD的定义、原理和重要性,以及如何在项目中实施CICD流程。 什…...

redis 高可用
Redis 高可用 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境中,高可用的含义似乎要宽泛一些,除了保证提供…...

什么样的词条可以创建维基百科?
维基百科在国内用得比较少,有一些特殊原因,维基百科的控制权海外,目前维基百科和谷歌是一样的,在国内是无法正常访问的。但做海外推广的朋友都是知道维基百科的,小马识途营销顾问认为它在世界互联网领域的地位…...

poll epoll初学习
正是select这些缺点,才有了poll 1.I/O多路转接之poll 2.I/O多路转接之epoll 其中的struct epoll_event:...
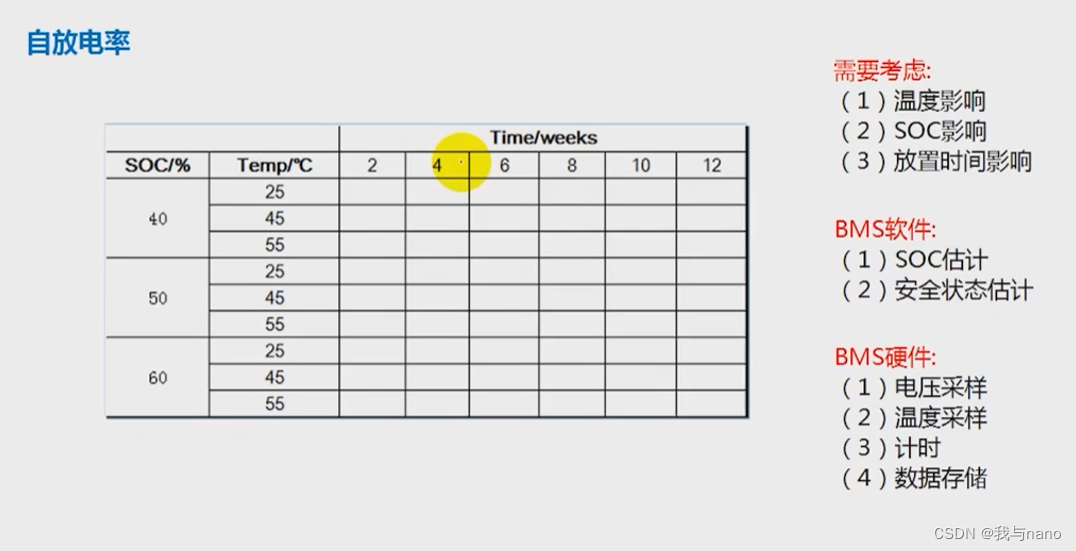
BMS电池管理系统——电芯需求数据(三)
BMS电池管理系统 文章目录 BMS电池管理系统前言一、有什么基础数据二、基础数据分析1.充放电的截至电压2.SOC-OCV关系表3.充放电电流限制表4.充放电容量特性5.自放电率 总结 前言 在新能源产业中电芯的开发也占有很大部分,下面我们就来看一下电芯的需求数据有哪些 …...
的问题)
【uniapp】关于小程序输入框聚焦、失焦(输入法占位)的问题
聊天小程序,界面带有输入框,当输入框中聚焦后,底部自动谈起输入法。此时输入框也要随之出现在输入法上方。默认情况下,输入框此时会被输入法覆盖掉。 以下是亲自实践,解决这个问题的方法: 一、小程序大概…...
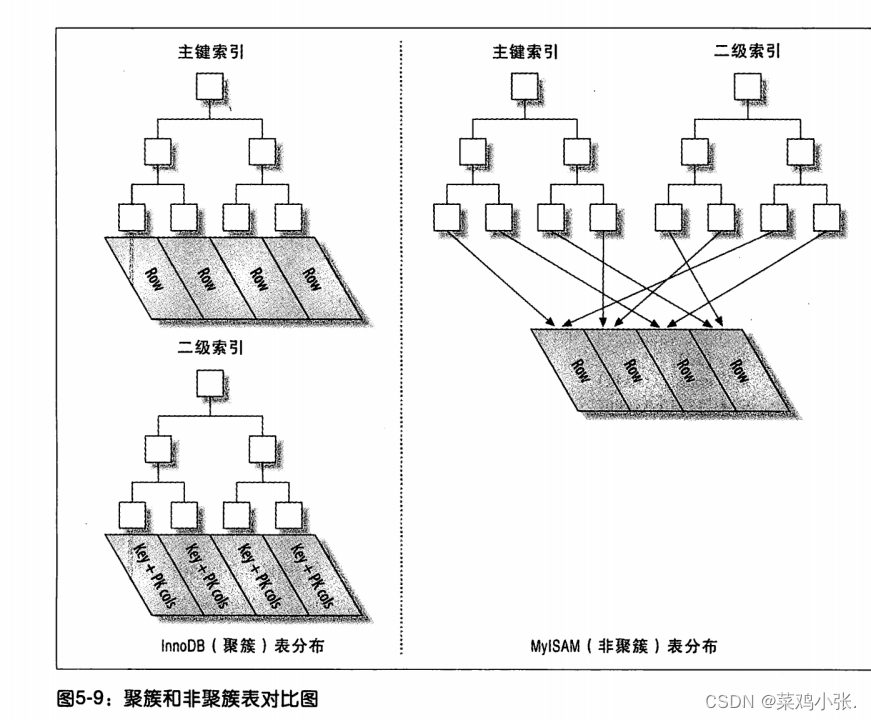
MySQL的故事——创建高性能的索引
创建高性能的索引 文章目录 创建高性能的索引一、索引基础二、索引的优点三、高性能的索引策略 一、索引基础 要理解MySQL中索引是如何工作的,最简单的方法就是去看看一本书的“索引 ”部分:如果在一本书中找到某个特定主题,一般会先看书的“…...

渗透测试漏洞原理之---【组件安全】
文章目录 1、组件安全概述1.1、常见组件1.1.1、操作系统1.1.2、Web容器1.1.3、中间件1.1.4、数据库1.1.5、开发框架1.1.6、OA系统1.1.7、其他组件 1.2、漏洞复现1.2.1 漏洞复现模板1.2.3、漏洞名称参考1.2.4、漏洞库 2、Apache2.1、Apache HTTPD2.2、Apache Shiro2.3、Apache T…...

uni-app集成mui-player
uni-app集成mui-player,仅说明集成方法,mui-player 相关配置请查看其官网 准备 在uniapp项目根目录新建hybrid目录在hybrid目录下新建html目录在html目录中新建css、js、img等目录,用于存放相关文件 集成 静态webview 在pages目录下新建v…...
算法_C++—— 两个数组的交集)
力扣(LeetCode)算法_C++—— 两个数组的交集
给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。 示例 1: 输入:nums1 [1,2,2,1], nums2 [2,2] 输出:[2] 示例 2: 输入:nums1 …...

异步编程 - 12 异步、基于事件驱动的网络编程框架 Netty
文章目录 Netty概述Netty中的一些概念Netty的线程模型Netty Server端Netty Netty 端 TCP半包与粘包问题基于Netty与CompletableFuture实现RPC异步调用 Netty概述 Netty是一个异步、基于事件驱动的网络应用程序框架,其对Java NIO进行了封装,大大简化了TC…...
STM32 Nucleo-144开发板开箱bring-up
文章目录 1. 开篇2. 开发环境搭建2.1 下载官方例程2.2 ST-Link安装 3. STM32F446ZE demo工程3.1 STM32F446ZE简介3.2 跑个demo试一试 1. 开篇 最近做项目,用到STM32F446ZET6这款MCU,为了赶进度,前期软件需要提前开发,于是在某宝买…...

计算机毕业设计 基于SSM的问卷调查管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
基于SpringBoot的无忌在线考试系统(源码+讲解+调试运行)做毕设课设均可
技术栈 前后端分离 前端使用: Vue Element Plus 后端使用: SpringBoot Mysql8.0 Mybatis-Plus 功能 分为 管理员端 和 老师端 和 学生端 管理员端 登陆页 科目管理 查看所有科目 ,增加 ,修改 ,删除科目 , 模糊搜索课程 考试管理 查看所有考试 ,增加 ,修改 ,删除考试 题库…...

无涯教程-JavaScript - EOMONTH函数
描述 EOMONTH函数返回该月最后一天的序列号,该序列号是start_date之前或之后的月份数。 语法 EOMONTH (start_date, months)争论 Argument描述Required/OptionalStart_date 代表开始日期的日期。 应该使用DATE函数或其他公式或函数的输出输入日期。 如果将日期作为文本输入…...

【LeetCode-面试经典150题-day21】
目录 120.三角形最小路径和 64.最小路径和 63.不同路径Ⅱ 5.最长回文子串 120.三角形最小路径和 题意: 给定一个三角形 triangle ,找出自顶向下的最小路径和。 每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标…...
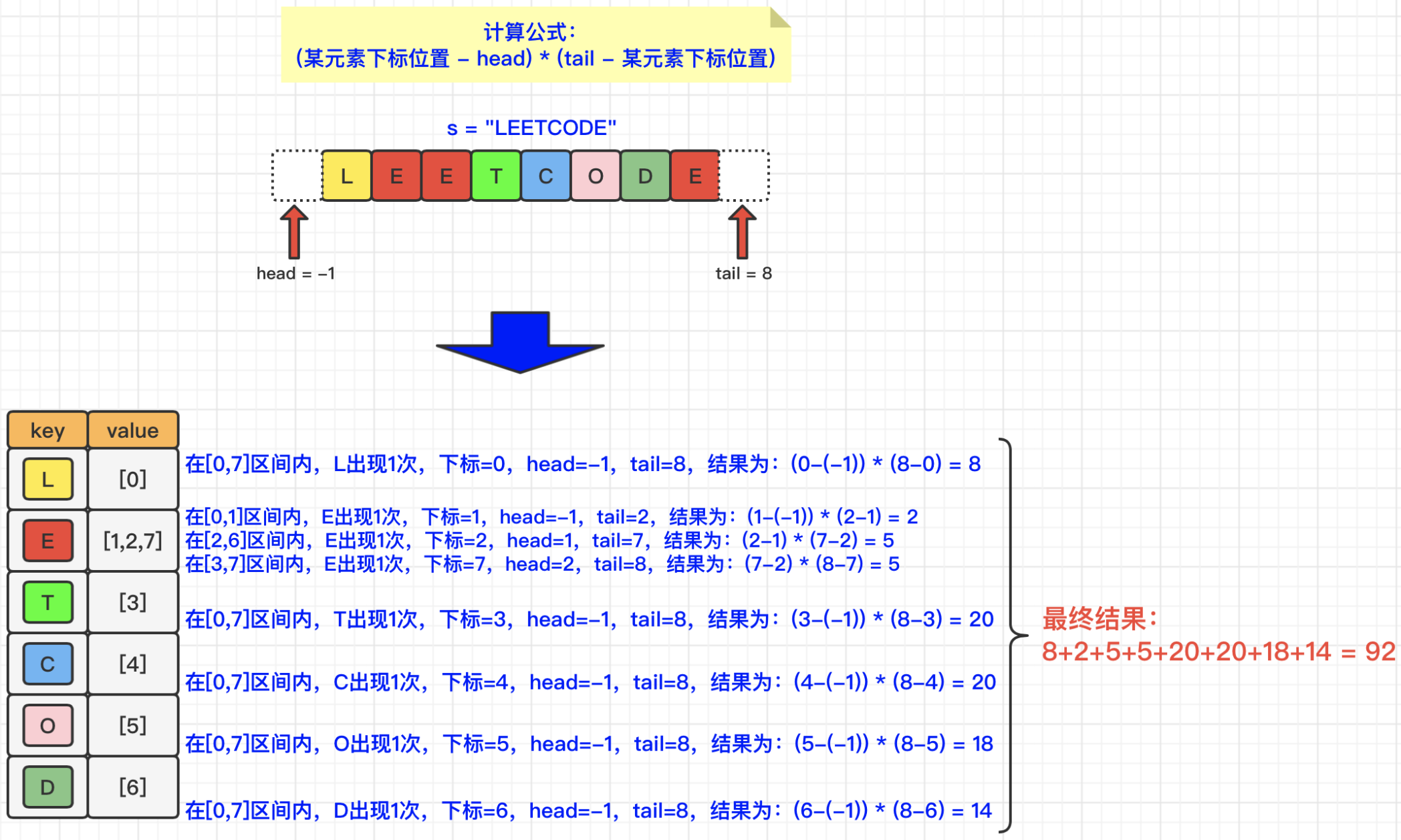
算法刷题记录-双指针/滑动窗口(LeetCode)
809. Expressive Words 思路 根据题目描述,我们可以知道,如果要将某个单词定义为可扩张(stretchy),需要满足如下两个条件: 所以,我们在实现的时候,可以通过两个指针p1和p2&#x…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
