概率论与数理统计学习笔记(7)——全概率公式与贝叶斯公式
目录
- 1. 背景
- 2. 全概率公式
- 3. 贝叶斯公式
1. 背景
下图是本文的背景内容,小B休闲时间有80%的概率玩手机游戏,有20%的概率玩电脑游戏。这两个游戏都有抽卡环节,其中手游抽到金卡的概率为5%,端游抽到金卡的概率为15%。已知小B这天抽到了金卡,那么请问他是在手机上抽到的还是在电脑上抽到的?

2. 全概率公式
上述问题中,我们先考虑小B抽到金卡这件事的概率,设玩电脑的概率为 P ( c ) P(c) P(c),玩手机的概率为 P ( p ) P(p) P(p),抽到金卡的概率为 P ( v ) P(v) P(v):
- 如果小B是在电脑上抽到的金卡,那么其概率为 P ( c ) P ( v ∣ c ) P(c)P(v|c) P(c)P(v∣c),就是玩电脑的概率乘上在电脑上抽到金卡的概率。
- 如果小B是在手机上抽到的金卡,那么其概率为 P ( p ) P ( v ∣ p ) P(p)P(v|p) P(p)P(v∣p),就是玩手机的概率乘上在手机上抽到金卡的概率。
上面两个式子分别计算了在手机上抽到金卡和在电脑上抽到金卡的概率,那么两者加起来就是小B抽到金卡的概率,即: P ( v ) = P ( c ) P ( v ∣ c ) + P ( p ) P ( v ∣ p ) P(v)=P(c)P(v|c)+P(p)P(v|p) P(v)=P(c)P(v∣c)+P(p)P(v∣p)。这就是全概率公式,简单来说就是该事件在所有可能的情况下发生的概率。
用一个图来表示更直观,如下图所示,是一个长宽为1的正方形,其面积代表了所有事件发生的可能性。玩电脑占了20%的面积,玩手机占了80%的面积;玩电脑抽到金卡,占了玩电脑这块区域里面的15%;玩手机抽到金卡,占了玩手机这块区域里面的5%。

那么抽到金卡的概率,即:

3. 贝叶斯公式
知道了全概率公式后,就很容易理解贝叶斯公式了。贝叶斯公式是建立在我们已经知道结果的情况下,即我们知道小B已经抽到金卡的情况下,反推小B是玩电脑抽到金卡的概率和玩手机抽到金卡的概率。
那么玩电脑抽到金卡的概率可以用图表达为:

表达为数学公式为:
P ( c ∣ v ) = P ( c ) P ( v ∣ c ) P ( v ) P(c|v)=\frac{P(c)P(v|c)}{P(v)} P(c∣v)=P(v)P(c)P(v∣c)
同理,玩手机抽到金卡的概率可以用图表达为:

表达为数学公式为:
P ( p ∣ v ) = P ( p ) P ( v ∣ p ) P ( v ) P(p|v)=\frac{P(p)P(v|p)}{P(v)} P(p∣v)=P(v)P(p)P(v∣p)
这里 P ( p ∣ v ) P(p|v) P(p∣v) 和 P ( c ∣ v ) P(c|v) P(c∣v) 称之为后验概率(posterior),即我们知道了结果,反推过程发生的概率; P ( c ) P(c) P(c) 和 P ( p ) P(p) P(p) 称之为先验概率(prior),即我们还暂时不知道后面的情况,在知道之前事件发生的可能性; P ( v ∣ c ) P(v|c) P(v∣c) 和 P ( p ∣ c ) P(p|c) P(p∣c) 称之为似然(likelihood),即在某个情况下,事件发生的可能性。
相关文章:

概率论与数理统计学习笔记(7)——全概率公式与贝叶斯公式
目录 1. 背景2. 全概率公式3. 贝叶斯公式 1. 背景 下图是本文的背景内容,小B休闲时间有80%的概率玩手机游戏,有20%的概率玩电脑游戏。这两个游戏都有抽卡环节,其中手游抽到金卡的概率为5%,端游抽到金卡的概率为15%。已知小B这天抽…...
深入了解 Axios 的 put 请求:使用技巧与最佳实践
在前端开发中,我们经常需要与后端服务器进行数据交互。其中,PUT 请求是一种常用的方法,用于向服务器发送更新或修改数据的请求。通过发送 PUT 请求,我们可以更新服务器上的资源状态。 Axios 是一个流行的 JavaScript 库࿰…...
浅谈Http协议、TCP协议(转载)
TCP标志位,有6种标示:SYN(synchronous建立联机) ,ACK(acknowledgement 确认) ,PSH(push传送),FIN(finish结束) ,RST(reset重置), URG(urgent紧急) Sequence number(顺序号码) ,Acknowledge num…...

flatten-maven-plugin使用
这篇文章主要介绍了flatten-maven-plugin使用,本文通过示例代码给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友可以参考下 − 目录 一、简介 1.1 作用1.2 goal介绍二、使用总结 一、简介 1.1 作用 将pom工程父子pom的版…...

Vue3中快速简单使用CKEditor 5富文本编辑器
Vue3简单使用CKEditor 5 前言准备定制基础配置富文本配置目录当前文章demo目录结构 快速使用demo 前言 CKEditor 5就是内嵌在网页中的一个富文本编辑器工具 CKEditor 5开发文档(英文):https://ckeditor.com/docs/ckeditor5/latest/index.htm…...

qt简易网络聊天室 数据库的练习
qt网络聊天室 服务器: 配置文件.pro QT core gui networkgreaterThan(QT_MAJOR_VERSION, 4): QT widgetsCONFIG c11# The following define makes your compiler emit warnings if you use # any Qt feature that has been marked deprecated (the exac…...
Navicat连接mysql8.0:提示无法加载身份验证插件“caching_sha2_password”
Navicat连接mysql时,提示:Unable to load authentication plugin ‘caching_sha2_password‘. 原因:mysql 8.0 默认使用 caching_sha2_password 身份验证机制。 D:\MySQL8.0\install\bin>mysql -uroot -p123456789 #登录 mysql: [War…...
手写签名到背景上合为1张图
手写签名到背景上合为1张图 package.json中 "signature_pad": "3.0.0-beta.3"<template><div class"home"><canvas id"canvas" width"500" height"300"></canvas><button click"…...

华为认证系统学习大纲及课程
前言 任何学习过程都需要一个科学合理的学习路线,才能够有条不紊的完成我们的学习目标。华为认证网络工程师所需学习的内容纷繁复杂,难度较大,所以今天特别为大家整理了一个全面的华为认证网络工程师学习大纲及课程,帮大家理清思…...

某米ax3000路由器组网解析
我们使用某米k60手机与某米ax3000 wifi6路由器组网,来分析和学习网络速率与瓶颈限制。 某米 AX3000 路由器简介 某米 AX3000 路由器是一款支持 WiFi 6 的双频路由器,它的 MIMO 是 22,也就是两根天线。MIMO 是 Multiple Input Multiple Outpu…...

【leetcode 力扣刷题】数学题之除法:哈希表解决商的循环节➕快速乘求解商
两道和除法相关的力扣题目 166. 分数到小数29. 两数相除快速乘解法一:快速乘变种解法二: 二分查找 快速乘 166. 分数到小数 题目链接:166. 分数到小数 题目内容: 题目是要我们把一个分数变成一个小数,并以字符串的形…...
方法-set.union())
Union类型和集合的union()方法-set.union()
Union类型和集合的Union 方法 一、Union类型1.Union类型由来2.Union类型的语法3.Union类型的使用4.一些等价写法 二、Set.union()union() 语法示例代码 一、Union类型 1.Union类型由来 Python中的Union类型是 3.10版本引入的新功能之一。它是一种特殊的类型注释,用…...
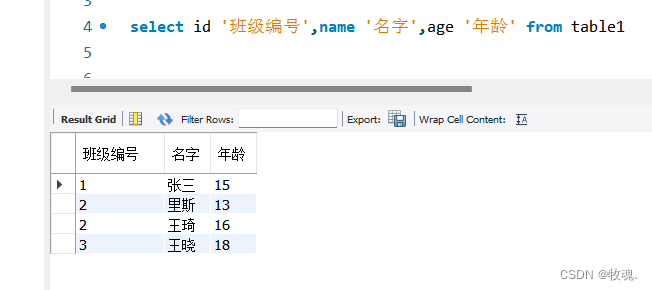
简明SQL别名指南:掌握AS实现列名更名
在 SQL 查询中,使用 {原始字段名} as {别名} 的语法来为查询结果的列赋予更直观的名称,以提高查询结果的可读性和可理解性。 以下是用到的表。 用AS更名 例如,查询表1的name字段,并将其更名为"名字",同时查…...

基于量子密钥分发和区块链技术的新一代加密通信系统
量子通信与区块链构建下一代加密通信基础设施 量子技术和区块链技术是国家信息安全和国家数字化转型的重要组成部分,在国家战略中具有重要地位。“十四五”规划纲要将“加快数字发展建设数字中国”作为独立篇章,指出要进一步明确发展云计算、大数据、物联…...

网络安全-子域名收集
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 子域名 子域名指二级域名,二级域名是顶级域名(一级域名)的下一级比如mail.heetian.com和bbs.heetian.com…...

go-zero jwt 鉴权快速实战
前面我们分享了 go-zero 的快速实战以及日志组件的剖析,本次我们来实战使用 go-zero jwt 鉴权 本次文章主要是分享关于 go-zero 中 jwt 的使用方式,会以一个 demo 的方式来进行实战,对于使用 goctl 工具以及安装细节就不在赘述,有…...

9.8day58 单调栈
739. 每日温度 - 力扣(LeetCode) 知识点:1.建栈 2.如果后面要加入的数小于栈顶元素就把数组的下标压进栈里 3.反之 就让该数于栈顶元素进行比较 如果该数大于栈顶元素(while) 就把栈顶元素下表对应的arr数组的值进行…...
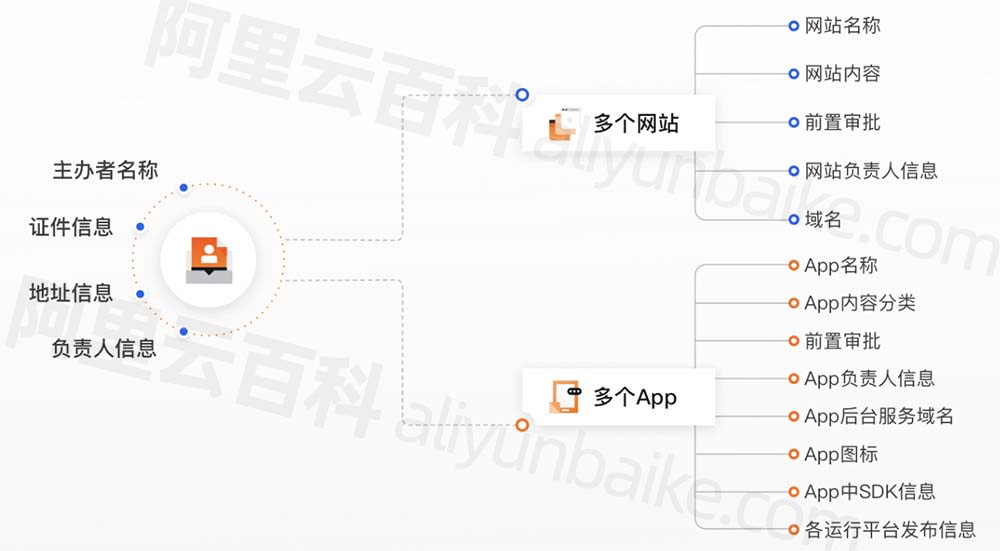
快速完成工信部APP备案流程_以阿里云APP备案为例
阿里云APP备案流程分为6步,APP备案成功后应用可以上架,登录阿里云账号填写APP信息,等待阿里云初审,初审通过后进行工信部短信核验,管局审核通过后APP即可备案成功,最后移动APP应用可以分发平台上架…...
uniapp中UView中 u-form表单在v-for循环下如何进行表单校验
1、数据data格式 注:rule绑定的tableFromRule中要和表单tableFrom下面放置一个同名数组,确保u-form能找到 tableFrom: {tableData: [//数据详情列表]},tableFromRule: {//校验tableData: [//数据详情列表]},formRules:{localation:[{required: true,mes…...

工作新时代,腾讯轻联塑造高效办公未来
腾讯轻联:开启便捷、高效的集成新纪元 ⭐ 写在前面⭐ 使用模板快速起步⭐ 自定义流程初体验⭐ 无与伦比的集成强者⭐ 写在最后 ⭐ 写在前面 在当今竞争激烈的商业环境中,提高企业的办公效率和工作流程自动化变得至关重要。腾讯轻联,作为新一…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
