决策树算法学习笔记
一、决策树简介
首先决策树是一种有监督的机器学习算法,其采用的方法是自顶向下的递归方法,构建一颗树状结构的树,其具有分类和预测功能。其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零。决策树的构建通常分为三个步骤:
1、特征选择
特征选择就是要选取具有较强分类能力的特征,分类能力通过信息增益或信息增益率来进行刻画。选择的标准是找出局部最优的特征作为判断进行切分,取决于切分后节点数据集合中类别的有序程度。衡量节点的数据集合的纯度有:信息增益(率)、基尼系数和方差(方差主要是针对回归的)。
2、决策树的生成
在决策树的生成算法中,常规的算法有ID3和C4.5生成算法。两者生成的过程类似,区别在于前者采用信息增益作为特征的度量,而后者采用信息增益率。但ID3和C4.5存在某些不足,因此改进的CART算法便产生了,它是采用基尼系数作为度量属性的选择。
3、决策树剪枝
决策树需要剪枝的原因是:决策树的生成算法生成的树对训练数据的预测很准确,但是对于未知的数据分类能力却很差,容易产生过拟合的现象。剪枝的过程是从已经生成的决策树上剪掉一些子树或者叶子节点。剪枝的目标是通过极小化决策树的整体损失函数或代价函数实现,其目的是提高模型的泛化能力。
二、决策树的生成算法
主要有ID3、C4.5和CART树算法。
首先来介绍ID3算法:
其思路是用信息增益的大小来判断当前节点应该用什么特征来构建决策树,用计算出的信息增益最大的特征来建立决策树的当前节点。
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即:
g(D,A)=H(D) – H(D|A)
其中H(D)度量了D的不确定性,H(D|A)度量了D在知道了A以后D剩下的不确定性,两者之差则度量了D在知道了A以后不确定性的减少程度。
ID3算法的不足:
1、其没有考虑连续特征,比如长度,密度都是连续值
2、其采用的信息增益大的特征优先建立决策树的节点。这就导致了在相同条件下取值较多的特征比取值较少的特征的信息增益 大。,例如一个变量有两个值,都为1/2,另一个变量有三个值,都为1/3,由于他们都是完全不确定的变量,但是取3个值的比取2个值的信息增益大。
3、ID3算法没有对于缺失值的情况做考虑。
4、ID3算法没有考虑过拟合的问题。
其次是C4.5算法
对于ID3算法存在的问题,C4.5对其做了进一步的改进。
首先对于不能处理连续特征的问题,C4.5的思路是将连续的特征离散化。比如m个样本的连续特征A有m个,从小到大排列为a1,a2...,am,则C4.5取相邻两样本值的平均数,一共取得m-1个划分点,其中第i个划分点Ti表示为:Ti=(ai+a(i+1))/2。对于这m-1个点,分别计算该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为at,则小于at的值为类别1,大于为类别2,这样就做到连续特征的离散化处理。
其次对于信息增益作为标准容易偏向于取值较多的特征的问题。引入了信息增益率作为度量特征的选择,它是信息增益和特征熵的比值。表达式如下:
Gr(D,A) = g(D,A) / HA(D)
信息熵g(D,A),H(A)为特征熵,对于H(A)其表达式如下:
其中n为特征A的类别数,Di为特征A的第i个取值对应的样本个数。D为样本个数。
再者,对于缺失值的问题,主要解决的问题主要有两个,一是在样本某些特征缺失的情况下选择划分的属性,二是选定了划分属性,对于在该属性上缺失特征的样本处理。
最后,对于过拟合的问题,C4.5引入了正则化系数进行初步的剪枝。
C4.5算法的不足:
1、C4.5剪枝的算法存在优化的空间。
2、C4.5算法生成的是多叉树,即一个父节点可以有多个节点。
3、C4.5只能用于分类
4、C4.5由于使用了熵模型,里面有大量的耗时的对数运算。
下面介绍CART算法:
CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益是相反的。
在分类问题中,假设有K个类别,第k个类别的概率为pk,则基尼系数的表达为:
如果是二分类为题,计算就更加简单,如果属于第一个样本输出的概率为p,则基尼系数的表达式为:
Gini(p)=2p(1-p)
对于给定的样本D,假设有K个类别,第k个类别的数量为Ck,则样本D的基尼系数表达式为:
Gini(D)=1-∑(|Ck|/|D|)^2特别地,对于样本D,如果根据特征A的某个值a,把D分为D1和D2两部分,则在特征A的条件下,D的基尼系数表达式为:
三、决策树CART算法的剪枝
目的:
对于没有进行剪枝的树,就是一个完全生长的决策树,是过拟合的,因此需要去掉一些不必要的节点以以提高训练出的决策树模型的泛化能力。
决策树算法剪枝的过程是由两个过程组成:
1、从T0开始不断的剪枝,直到剪成一颗单节点的树,这些剪枝树形成一个剪枝树序列{T0,T1,T2...,Tn}。
2、从上面形成的剪枝序列中挑选出最优剪枝树。方法是:通过交叉验证法使用验证数据集对剪枝树序列进行测试。
首先,给出决策树算法的损失函数:
Cα(T)=C(T)+α|T| 其中C(T)为决策树对训练数据的预测误差:|T|为决策树的叶子节点数对固定的α,存在使Cα(T)最小的树,令其为Tα,可以证明Tα是唯一的。
当α大时,Tα偏小(即决策树比较简单)
当α小时,Tα偏大(即决策树比较复杂)
当α=0时,生成的决策树就是最优的
当α为无穷时,根组成的一个单节点树就是最优的。
考虑生成树T0.对T0内的任意节点t,以t为单节点树(记作t')的损失函数为:Cα(t')=C(t')+α,以t为根的子树Tt的损失函数为:
Cα(Tt)=C(Tt)+α|Tt|。可以证明:
当α=0及充分小时,有Cα(Tt)<Cα(t')
当α增大到某个值时,有Cα(Tt)=Cα(t')
当α再增大时时,有Cα(Tt)>Cα(t')
因此令α=(C(t'<C(Tt)))/(|Tt|-1),此时t'与Tt有相同的损失函数值,但是t'的叶节点更少,于是对Tt进行减值成一颗单节点树t'了。
对T0内部的每一个节点t,定义g(t)=(C(t'<C(Tt)))/(|Tt|-1)。设T0内g(t)最小的子树为Tt*,令该最小值的g(t)为α1'。从T0中剪去Tt*,即得到剪枝树T1,重复这种“求g(t)-剪枝”过程,直到根节点即完成剪枝。在此过程中不断增加αi'的值,从而生成剪枝树序列。
CART剪枝交叉验证过程是通过验证数据集测试剪枝树序列{T0,T1,T2...,Tn}中个剪枝树的。对于CART回归树,是考察剪枝树的平方误差,平方误差最小的决策树被认为是最有决策树。对于CART分类树,是考察基尼指数,基尼指数最小的决策树被认为是最优的决策树。
四、决策树代码实例
下面是一个使用Python的scikit-learn库实现决策树的代码示例
# 导入所需的库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree# 加载数据集
iris = load_iris()
X = iris.data # 特征向量
y = iris.target # 目标变量# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)# 创建决策树分类器
clf = DecisionTreeClassifier(max_depth=3, random_state=1)# 训练决策树模型
clf.fit(X_train, y_train)# 使用训练好的模型进行预测
y_pred = clf.predict(X_test)# 计算准确率
accuracy = metrics.accuracy_score(y_test, y_pred)
print("准确率:", accuracy)# 可视化决策树
plt.figure(figsize=(10, 6))
plot_tree(clf, filled=True, rounded=True, feature_names=iris.feature_names, class_names=iris.target_names)
plt.show() 以上代码实现了对鸢尾花数据集的分类任务。首先,导入所需的库。然后,加载鸢尾花数据集,其中X是特征向量,y是目标变量。接着,将数据集划分为训练集和测试集,其中测试集占总数据集的30%。然后,创建一个决策树分类器,并指定最大深度为3和随机种子为1。
在决策树模型中,设置最大深度可以控制决策树的复杂度,避免过拟合。较小的最大深度可以降低模型的复杂度,但也可能导致欠拟合。随机种子用于重现结果,确保每次运行代码时得到相同的结果。
接着,使用训练集对决策树模型进行训练。然后,使用训练好的模型对测试集进行预测并得到预测结果y_pred。
使用metrics.accuracy_score函数计算预测准确率,并将结果打印出来。
最后,使用matplotlib库将决策树可视化显示出来。通过调用plot_tree函数并传入决策树模型、特征名和目标类别名等参数,可以生成决策树的图形化显示。
相关文章:
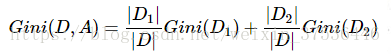
决策树算法学习笔记
一、决策树简介 首先决策树是一种有监督的机器学习算法,其采用的方法是自顶向下的递归方法,构建一颗树状结构的树,其具有分类和预测功能。其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零。决策树的构…...

Verilog_mode常用的几个用法
一:verilog mode中如何使用正则表达 在顶层实例化时,有大量的信号需要重新命名,使用模板的话会增加大量的注释内容,不过往往这些信号命名有特定的规律,我们可以使用正则表达式来处理,下面举几个例子&#…...

MySQL之MHA高可用配置及故障切换
目录 一、MHA概念 1、MHA的组成 2、MHA的特点 3、主从复制有多少种复制方法 二、搭建MySqlMHA部署 1.Master、Slave1、Slave2 节点上安装 mysql 2.修改 Master、Slave1、Slave2 节点的 Mysql主配置文件/etc/my.cnf 3. 配置 mysql 一主两从 4、安…...

java实现状态模式
状态模式是一种行为设计模式,它允许对象在内部状态改变时改变其行为。在状态模式中,对象将其行为委托给表示不同状态的状态对象,这些状态对象负责管理其行为。以下是在 Java 中实现状态模式的一般步骤: 创建一个状态接口ÿ…...
)
Selling a Menagerie(cf)
该题考察了拓扑排序dfs 题意:你是一个动物园的主人,该动物园由编号从1到n的n只动物组成。然而,维护动物园是相当昂贵的,所以你决定卖掉它!众所周知,每种动物都害怕另一种动物。更确切地说,动物…...

python-55-打包exe执行
目录 前言一、pyinstaller二、实践打包exe1、遇坑1:Plugin already registered2、遇坑2:OSError 句柄无效 三、总结 前言 你是否有这种烦恼? 别人在使用你的项目时可能还需要安装各种依赖包?别人在使用你的项目,可能…...

linux并发服务器 —— IO多路复用(八)
半关闭、端口复用 半关闭只能实现数据单方向的传输;当TCP 接中A向 B 发送 FIN 请求关闭,另一端 B 回应ACK 之后 (A 端进入 FIN_WAIT_2 状态),并没有立即发送 FIN 给 A,A 方处于半连接状态 (半开关),此时 A 可以接收 B…...
企微SCRM营销平台MarketGo-ChatGPT助力私域运营
一、前言 ChatGPT是由OpenAI(开放人工智能)研发的自然语言处理模型,其全称为"Conversational Generative Pre-trained Transformer",即对话式预训练转换器。它是GPT系列模型的最新版本,GPT全称为"Gene…...
linux C++ 海康截图Demo
项目结构 CMakeLists.txt cmake_minimum_required(VERSION 3.7)project(CapPictureTest)include_directories(include)link_directories(${CMAKE_SOURCE_DIR}/lib ${CMAKE_SOURCE_DIR}/lib/HCNetSDKCom) add_executable(CapPictureTest ${CMAKE_SOURCE_DIR}/src/CapPictureTes…...

MySQL的事务隔离级别
目录 事务隔离级别的概念 脏读(Dirty Read): 不可重复读(Non-Repeatable Read): 幻读(Phantom Read): 读未提交(Read Uncommitted) 读未提交…...

企业大语言模型智能问答的底层基础数据知识库如何搭建?
企业大语言模型智能问答的底层基础数据知识库搭建是一个复杂而关键的过程。下面将详细介绍如何搭建这样一个知识库。 确定知识库的范围和目标: 首先,需要明确知识库的范围,确定所涵盖的领域和主题。这可以根据企业的业务领域和用户需求来确…...
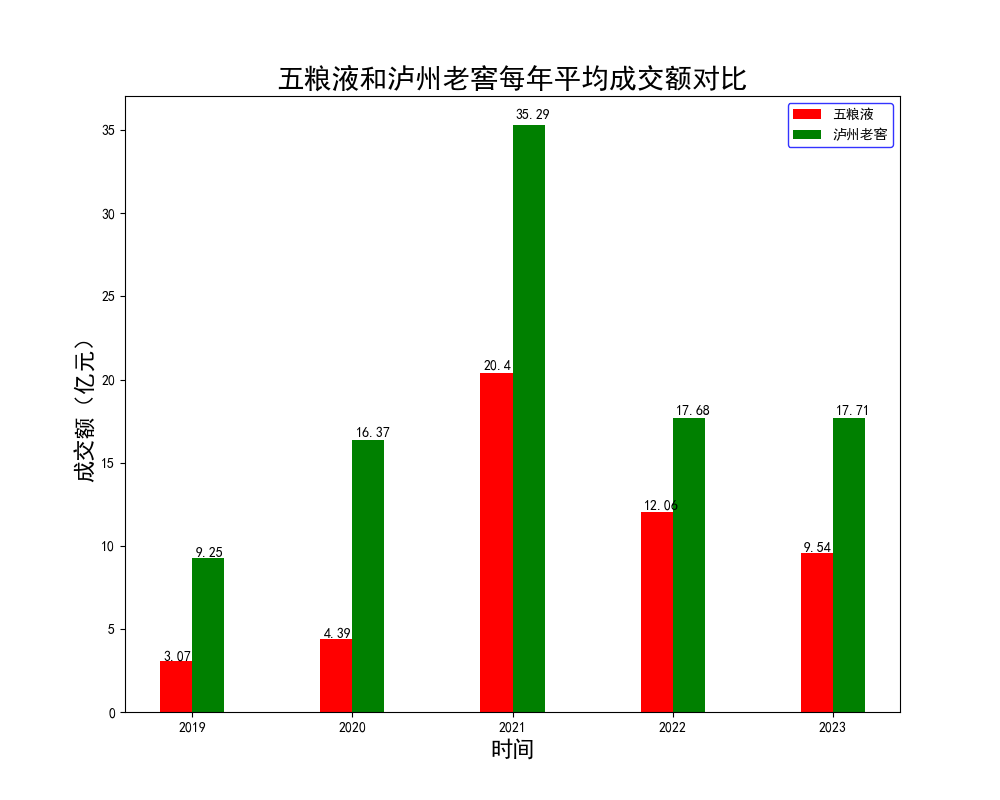
【腾讯云 Cloud Studio 实战训练营】使用python爬虫和数据可视化对比“泸州老窖和五粮液4年内股票变化”
Cloud Studio 简介 Cloud Studio是腾讯云发布的云端开发者工具,支持开发者利用Web IDE(集成开发环境),实现远程协作开发和应用部署。 现在的Cloud Studio已经全面支持Java Spring Boot、Python、Node.js等多种开发模板示例库&am…...

Linux之Shell概述
目录 Linux之Shell概述 学习shell的原因 shell是什么 shell起源 查看当前系统支持的shell 查看当前系统默认shell Shell 概念 Shell 程序设计语言 Shell 也是一种脚本语言 用途 Shell脚本的基本元素 基本元素构成: Shell脚本中的注释和风格 Shell脚本编…...

手写Spring:第2章-创建简单的Bean容器
文章目录 一、目标:创建简单的Bean容器二、设计:创建简单的Bean容器三、实现:创建简单的Bean容器3.0 引入依赖3.1 工程结构3.2 创建简单Bean容器类图3.3 Bean定义3.4 Bean工厂 四、测试:创建简单的Bean容器4.1 用户Bean对象4.2 单…...

在Windows上通过SSH公私钥实现无密码登录Linux
在Windows上通过SSH公私钥实现无密码登录Linux 在Windows上生成SSH密钥对: 打开命令提示符或PowerShell窗口。 输入以下命令生成SSH密钥对: ssh-keygen -t rsa -b 4096按照提示输入密钥的保存路径和密码(可选)。 在指定的路径下…...
使用ppt和texlive生成eps图片(高清、可插入latex论文)
一、说明 写论文经常需要生成高清的图片插入到论文中,本文以ppt画图生成高质量的eps图片的实现来介绍具体操作方法。关于为什么要生成eps图片,一个是期刊要求(也有不要求的),另一个是显示图像的质量高。 转化获得eps…...
)
html5学习笔记19-SSE服务器发送事件(Server-Sent Events)
https://www.runoob.com/html/html5-serversentevents.html 允许网页获得来自服务器的更新。类似设置回调函数。 if(typeof(EventSource)!"undefined"){var sourcenew EventSource("demo_sse.php");source.onmessagefunction(event){document.getElement…...
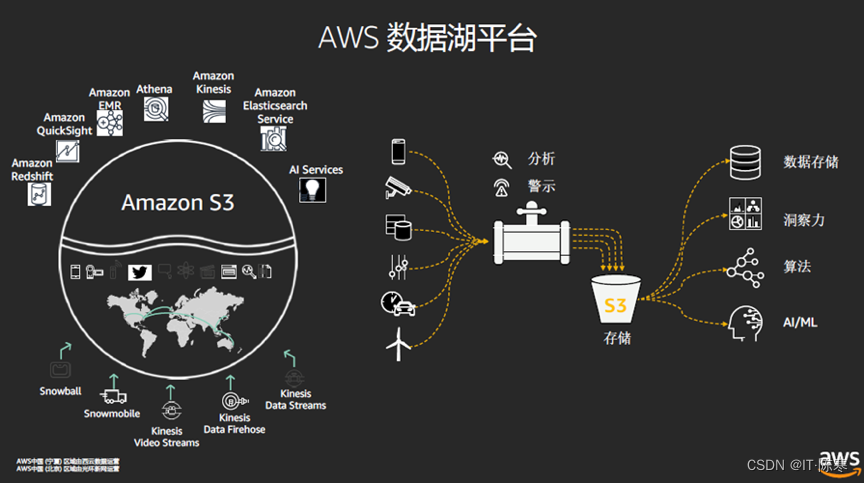
高效数据湖构建与数据仓库融合:大规模数据架构最佳实践
文章目录 数据湖和数据仓库:两大不同理念数据湖数据仓库 数据湖与数据仓库的融合统一数据目录数据清洗和转换数据安全和权限控制数据分析和可视化 数据湖与数据仓库融合的优势未来趋势云原生数据湖自动化数据处理边缘计算与数据湖融合 结论 🎉欢迎来到云…...

Java学习笔记——35多线程02
线程同步 线程同步卖票案例同步代码块同步方法块 线程安全的类StringBufferVectorHashtable Lock锁 线程同步 卖票案例 public class SellTicket implements Runnable{private int tickets10;Overridepublic void run(){while (true){if(tickets>0){System.out.println(Th…...

每日刷题-3
目录 一、选择题 二、编程题 1、计算糖果 2、进制转换 一、选择题 1、 解析:在C语言中,以0开头的整数常量是八进制的,而不是十进制的。所以,0123的八进制表示相当于83的十进制表示,而123的十进制表示不变。printf函数…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...


